基于耦合映像格子模型的电光双稳系统的时空混沌控制

(1．长春理工大学光电信息学院，吉林长春130000;2．吉林大学原子与分子研究所，吉林长春130000)

目前广义混沌可大致分为3类:时间混沌，时空混沌，空间混沌．近些年来，国际上很多人提出了混沌控制的方法，相比较而言，提出的时间混沌控制研究的方法较多，例如，驱动响应同步，非线性反馈法，外力反馈控制法等，然而时空混沌的研究相对较少，且时空混沌的保密性更高，科学家们常用六种斑图来描述时空混沌行为［1-3］，常采用时间混沌控制的方法对每一个格点进行控制，因此时空混沌控制也可分为线性反馈和非线性反馈，本文采用的是常数偏移法，属于线性反馈的方法，通过选取不用的参数实现时空混沌不同斑图的控制，以往的时空混沌的控制很少针对某一参数下的行为进行研究，在参数的选择方面有一定的局限，本文基于耦合电光双稳映像格子模型，在一定的参数下，用计算机模拟的方法得到适当的偏移常数和几种时空混沌控制斑图，弥补了时空混沌领域对参数选择的不足．

1 耦合电光双稳映像格子模型

考虑一个既包含时间又包含空间的系统，若讨论空间所有点的状态随时间变化的行为，则应写成偏微分方程的形式(1):

式中n表示离散化后的时间变量，用周期性边界条件为xn(0)=xn(L)．

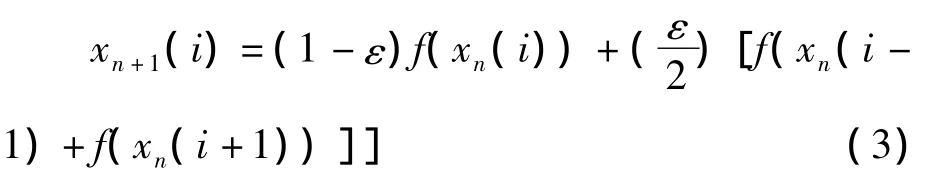
其中u表示为状态矢量，x表示为空间矢量，t是时间变量，反应扩散的过程可表示为(2):

可以将反应扩散过程分解为局部反应过程和扩散过程同时进行的两个过程，通过并行一个非线性映像来描述局部反映过程，扩散过程可以通过将拉普拉斯算

子离散化得到，最后可得到一维耦合映像格子模型［10］(3)．

2 空间振幅变化图和时空行为发展图

输入光强 I=6．1，消光系数 K=0．8，耦合系数ε=0．1时，耦合电光双稳系统映像格子模型每个格点的Lyapunov指数模型的变化如图1．

K=0．8，，I=6．1 而当考虑 100 个格点时，则每个格点在每个时刻都处于混沌的状态，这就是时间混沌和时空混沌的区别和联系，显然时空行为的复杂性更高，因此每个格点的状态与其系统整体的状态并不相同，在实际应用中，应根据不同的系统采用不同的控制方法进行有效的控制．

图1 k=0．8，ε=0．1 时，耦合电光双稳系统每个格点的Lyapunov指数

当 k=0．8，ε =0．1 时，从时空行为发展图中可以看出:任何一个小空间都不能发现任何有序行为，也就是说此时整个时空系统发生了混沌行为，如图2～3．

图2 k=0．8，ε=0．1 时，耦合电光双稳映像格子模型的空间振幅变化图

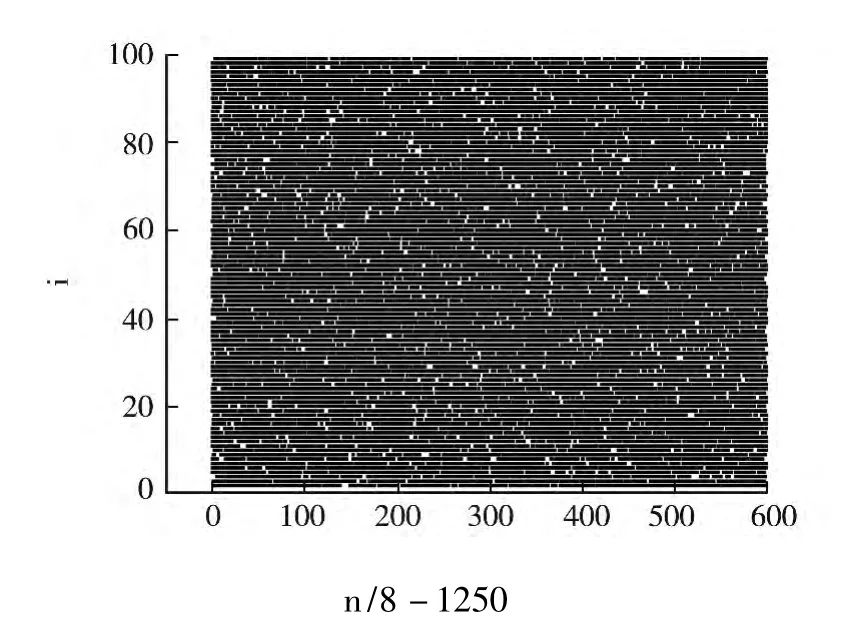
图3 k=0．8，ε=0．1 时，耦合电光双稳映像格子模型的时空行为发展图

通过对于许多耦合映像格子模型六种模式的研究，展示了时空行为的本质和规律．

3 混沌的控制

利用常数偏移法控制时空模型的动力学方程可写为(4):

其中常数ζ代表在迭代中的偏移强度，局域动力学函数f(xn(i))为电光双稳态映象式，系统参数取 a=π，I=6．1，k=0．8，ε =0．1，周期边界条件xn(1)=xn(L)=0，随机的初始条件，系统长度．

我们运用计算机模拟的方法，可以将偏移常数选择在一定的范围内进行多次的尝试，由于此过程完全有计算机来完成，所以计算的时间较短，我们只通过origin图像便可得知在哪些偏移常数的范围内可以实现时空混沌的控制，在实际的应用中我们可以根据需要选择不同的偏移常数控制时空混沌．

图4 偏移系数为1．7时，第50个格点的时序图

如图4是ζ=1．7时，去掉5 000步暂态过程，在系统进行到第10 000步开始控制，成功的将混沌控制在单周期轨道的情形．若不对系统施加控制，则第50个格点的时空序列如上图，当时间足够长时，这个格点由混沌态过渡到4周期态，并长期处于四周期态，因此这种方法不仅可以控制混沌还可改变给点的周期态．

4 结 论

混沌的反控制是将处于与周期太的系统使用某种手段，使系统处于混沌态，用常数便宜发可以通过改变偏移常数的大小也可以进行混沌的反控制，以往人们对混沌控制的研究较多［11-12］，却忽略了混沌的反控制，因为在气象学，电子电路，经济学中均会出现混沌，有时需要我们对混沌进行反控制，本文中的常数偏移法既是混沌控制的方法，也是个很好的反控制方法，混沌的反控制在军事上也有很重要的意义．

［1］ 杨维明．时空混沌和耦合映像格子［M］．上海:上海科技教育出版社，1994:17-24．

［2］ Hugues Chate，Paul Manneville．Spatio-temporal intermittency in coupled map lattices［J］．Physica D:Nonlibear Phenomena，1985，32(3):409-422．

［3］ K．Kaneko．Pattern competition intermittency and selective flicker noise in spatio-temporal chaos［J］．Phys．Lett．A，1987，125(1):25-31．

［4］ 崔艳斌，张平．混沌控制理论在生物医学研究中的应用［J］．医疗装备，2014，12(27):17-20．

［5］ 张旭东，朱萍，谢小平，等．混沌神经网络的动态阈值控制［J］．物理学报，2013，21(62):201506-1-7．

［6］ 杨杨，张雪锋，张雁冰．于耦合映像格子的分组图像加密算法［J］．西安邮电学院学报，2012，17(1):30-33．

［7］ 陈宇环，小红，称福．基于耦合映像格子的时空混沌同步保密通信研究［J］．计算机应用及软件，2008，25(5):74-76．

［8］ 王永，雷鹏．一种基于Baker映射与时空混沌的图像加密算法［J］．重庆邮电大学学报:自然科学版，2015，27(4):556-562．

［9］ 魏旭晖，王辉．异构网络下TCP拥塞控制的混沌特性分 析［J］．系 统 仿 真 学 报，2015，27(7):1541-1547．

［10］卢侃等编译．混沌动力学［M］．上海:上海翻译出版公司，1990:23-56．

［11］ Szmoski，Romeu M，Pereira，et al．Effective dynamics for chaos synchronization in networks with time-varying topology［J］．Commumization in nonlinear science and numerical simulation ，2012，18(6):1491-1498．

［12］ Acosta A．，Garcia P，Leiva H．shynchronization of non-identical extended chaotic systems［J］．Applicableanalysis 2012，92(4):740-751．