球面4R引纬机构运动及载荷特性研究*
2015-03-02周香琴王琴龙
江 浙 ,周香琴* ,王琴龙
(1.浙江理工大学现代纺织装备重点实验室,浙江杭州310018;2.万利纺织机械研究院,浙江杭州310018)
0 引 言
引纬机构是剑杆织机的重要部件之一,它的功能是将纬纱引入由经纱所形成的梭口,从而交织成所需的织物纹理。对此的工艺要求较为严格,如与开口、打纬的时间配合,以及平稳准确性、高速适应性、产品适应性等,这些因素直接影响到织物的质量[1]。在现代剑杆织机的发展中,空间球面四连杆的引纬方式越来越受到重视,Picanol、Sulzer、苏吴机械等公司均有相关型号的织机投入生产。其结构中的球面4R 机构设计独特[2],通过铰链副连接增加结构紧凑性和准确性,运转速度快,占地体积小,成本低。目前许多学者针对球面4R 机构做了研究[3-5],大多是探寻剑带运动规律数学模型,利用等效转动惯量的概念分析各构件对主轴驱动载荷的影响,并且通过三维仿真软件验证,较少涉及空间连杆的运动特性及载荷特性分析。国内剑杆织机厂家虽然能生产球面4R 引纬机构,但大多属仿制,在机构的参数及结构设计方面的创新较少,对机构中各构件的运动特性及载荷特性研究较少,特别是空间连杆构件[6-8]。
本研究试图通过数值分析的方法,针对剑杆织机引纬机构中的球面4R 机构4 个轴线方向的运动进行解析,利用几何等同性的概念和方向余弦法取代等效转换,省去不必要的计算。从运动学和动力学两方面,对叉形连杆的进行详细分析,为球面4R 引纬机构设计与改进提供论据。
1 GTM 剑杆织机引纬机构介绍
剑杆织机引纬驱动机构的机构简图如图1 所示。驱动轴带动旋转臂1 作圆周转动,带动与旋转臂1 相连的叉形连杆2 做空间运动,叉形连杆2 的运动可看做是两种摆动的叠加,即绕CD 轴线的往复摆动,和绕O 轴线的往复摆动。十字节3 通过两端轴承与叉形连杆2 连接。旋转臂1、叉形连杆2、十字节3、箱体0 形成的4 个转动副轴线交于一点O,形成一个球面4R 机构;十字节3、H 形连杆4、扇形齿轮5、箱体0 形成平面四杆机构。通过改变扇形齿轮槽中铰接点G 的位置,可实现剑头动程的调节,该点上移时,剑杆动程减小;反之,剑杆动程增加,从而控制剑杆织机的织造幅宽。扇形齿轮5 与传剑轴6 啮合传动,起到剑头运动动程的放大作用。固定在传剑轴上的剑轮带动剑带与剑头做直线往复运动,实现引纬运动。
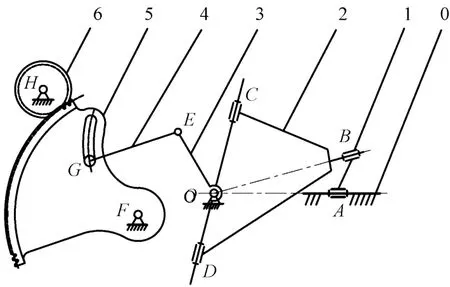
图1 GTM 剑杆织机引纬驱动机构简图
2 球面4R 机构运动函数的推导
球面4R 机构简图如图2 所示。将坐标系原点定在4 个转动副轴线交点O,建立OXYZ 坐标系。在4R机构的各杆上,固结有相应的坐标系。设旋转臂1 与箱体的相对运动轴线为Z0轴,以此类推建立Z1、Z2、Z3轴,如图2 所示。X3为Z2和Z3两轴的公垂线,以此类推建立X0、X1、X2轴。驱动轴逆时针方向旋转为正,图2 位置旋转180°后,Z0,Z1,Z2处于同一平面时,设定为初始位置。
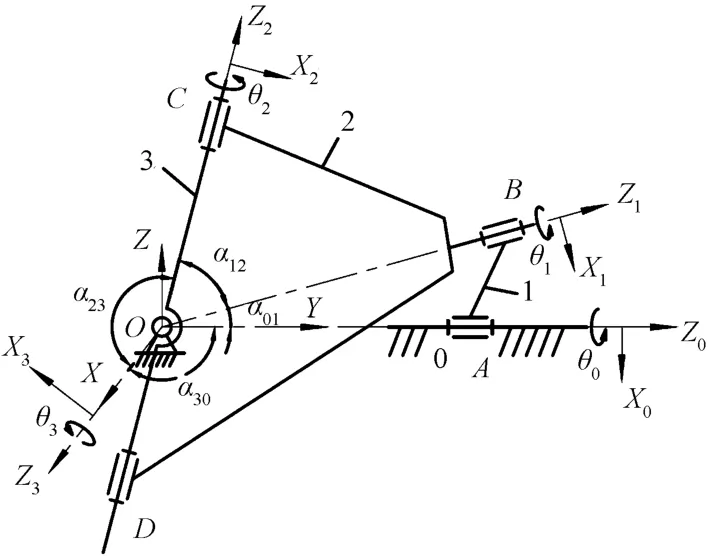
图2 球面4R 机构简图
为了直接建立输出转角θ2和输入转角θ0的关系式,可假想将机构拆分为浮动链2—3 和连架链0—1。由机构运动的几何等同性理论[9]可知,从连架链计算拆分的两轴线夹角方向余弦必定与从浮动链计算的结果相同,即:
(0,0,1)[C12][C23](0,0,1)T=(0,0,1)[C30][C01](0,0,1)T
由此可得:
-cosθ3sinα12sinα23+cosα12cosα23=-cosθ1sinα30sinα01+cosα30cosα01
式中:α01,α12,α23,α30—Z0与Z1,Z1与Z2,Z2与Z3,Z3与Z0的夹角。笔者所研究的机构中,α23=α30=90°,化简整理,得:
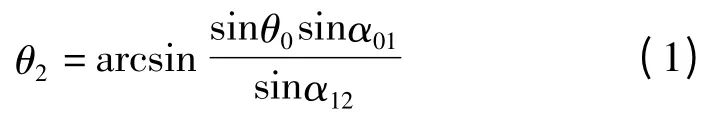
式(1)为球面4R 引纬机构的运动函数方程,其中α01,α12—结构参数(在该机构中α01=33°,α12=57°)。令η=f(θ0)-f(0°),即表示相对于初始位置的运动关系。
根据关注区域所有注视点持续时间总和数据(TFD),页面12的电路符号区域(“Rectangle2”)的TFD平均值最大,标题区域(“Rectangle”)的TFD平均值最小。页面13的卡通小人区域TFD平均值最长,而电路符号、电器元件三维图区域(电器零件2、电器零件1)TFD平均值小得多。页面12的TFD数据说明学生时间主要花在学习重、难点内容,而页面13的TFD数据说明学生被趣味性内容(卡通形象吸引),没有花更多时间学习重、难点内容。从提升课件学习效率看,页面12的简洁设计更好。但适当地插入趣味性的内容,可以提高学生的学习兴趣。
3 函数特性研究
3.1 函数单调性

由于有文献已经证实[10],机构的存在条件为α01<α12<π-α01,则sinα01<sinα12,所以1/ξ >0,当θ0在时,dθ2/dθ0<0,单调递减;当θ0在时,dθ2/dθ0≥0,单调递增,k=0,1,2,3……。
3.2 极值
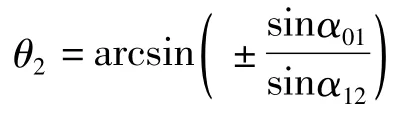
由此得到极差为:
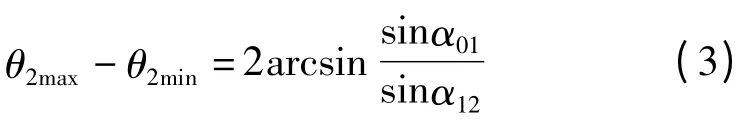
本研究设定α12=57°,α01取不同的数值,α01对极值影响如图3 所示;设定α01=33°,α12取不同的数值,α12对极值影响如图4 所示,分析其对极值的影响。
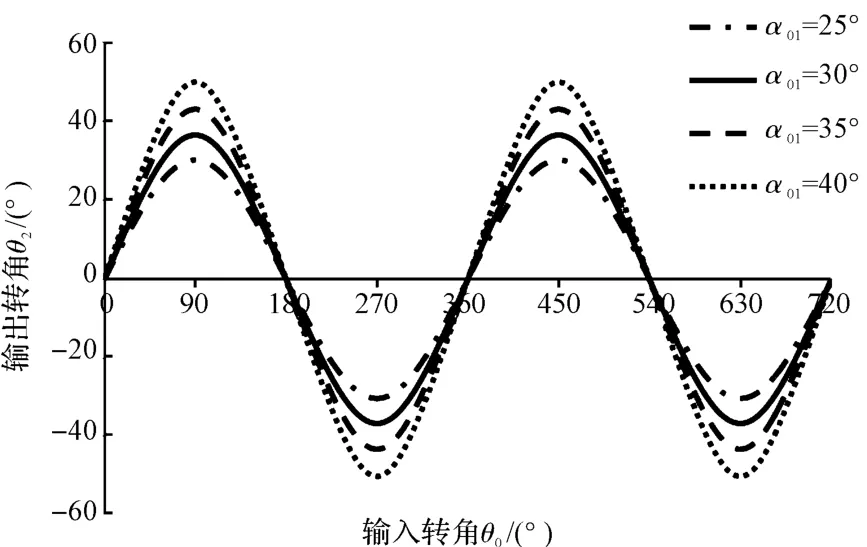
图3 α01对极值影响
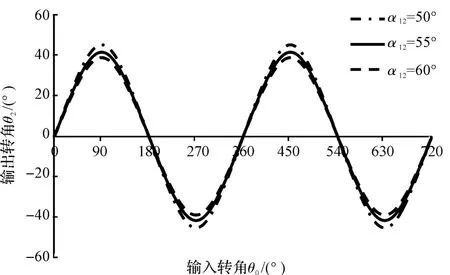
图4 α12对极值影响
同样可得[10]:
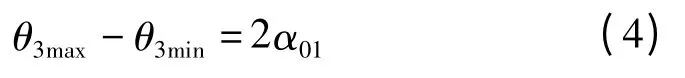
3.3 中心对称性
对于式(1),易证f(θ0)=-f(2π-θ0),f(θ0)=f(π-θ0),则由公式得到的曲线关于点(180°,0)中心对称,并且关于轴线θ0=90°对称。由此可知,叉形连杆绕图1 中CD 轴线的往复摆动是对称的,叉形连杆与十字节可以考虑对称设计。
4 载荷特性分析
4.1 动能计算
该引纬机构叉形连杆的动能计算式为:
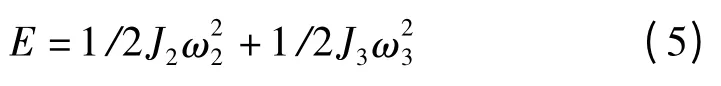
式中:J2,J3—绕Z2、Z3的转动惯量,J2可利用Pro/E中的实体物性计算直接获得,
当Z2与Z0垂直时,此时刻叉形连杆对Z3的转动惯量记为,所以得到任意时刻该转动惯量表达式:
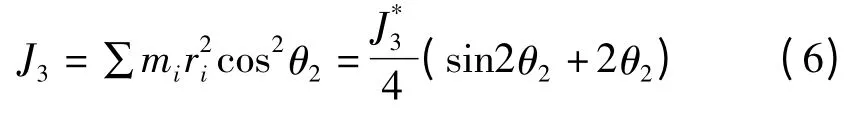
由此可得动能表达式:
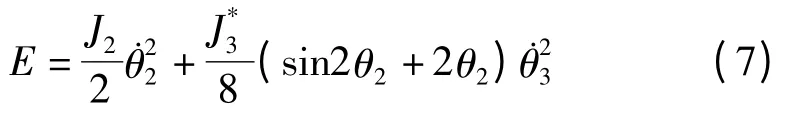
4.2 惯性力矩计算
叉形连杆的惯性力矩可以理解为分别绕Z2和Z3轴旋转的两个惯性力矩,其中,绕Z2轴的惯性力矩为M2=J2α2,其中,α2=。假设当Z2与Z0垂直时,此时刻质心到旋转中心轴的距离为一定值,则绕Z3轴的惯性力矩为M3=J3α3,其中:。惯性力矩分解为坐标系三方向Mx= J3α3,My= J2α2sinθ3,Mz=J2α2cosθ3。其中:α2,α3,J2,θ3—关于θ0的函数,因此,惯性力矩同样受单因子影响。
4.3 重要轴承力计算
本研究对叉形连杆2 受力分析,建立坐标系,轴承B 为滚针轴承,Fb1、Fb2是两个相互垂直的径向力,Fb2位于OAB 平面。轴承C、D 为圆锥滚子轴承,其轴向力F3沿CD 方向,径向力Fc2位于β 平面,Fc1与Fc2、F3两两垂直。Fd1、Fd2的方向以此类推,叉形连杆受力分析图如图5 所示。4R 机构相关符号说明如表1 所示。列出平衡方程:
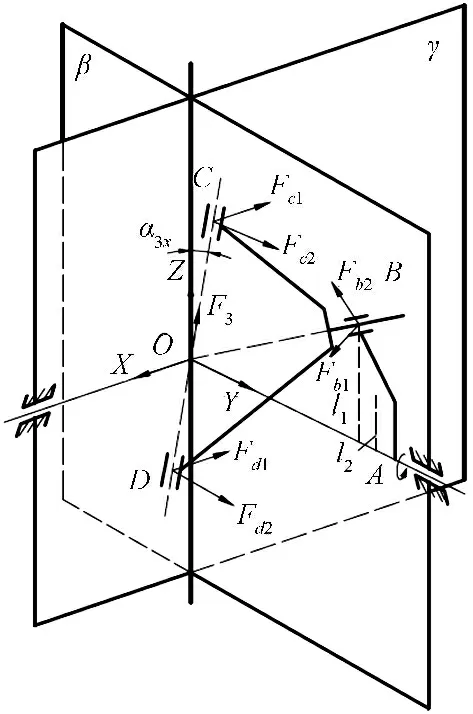
图5 叉形连杆受力分析图

表1 4R 机构相关符号说明
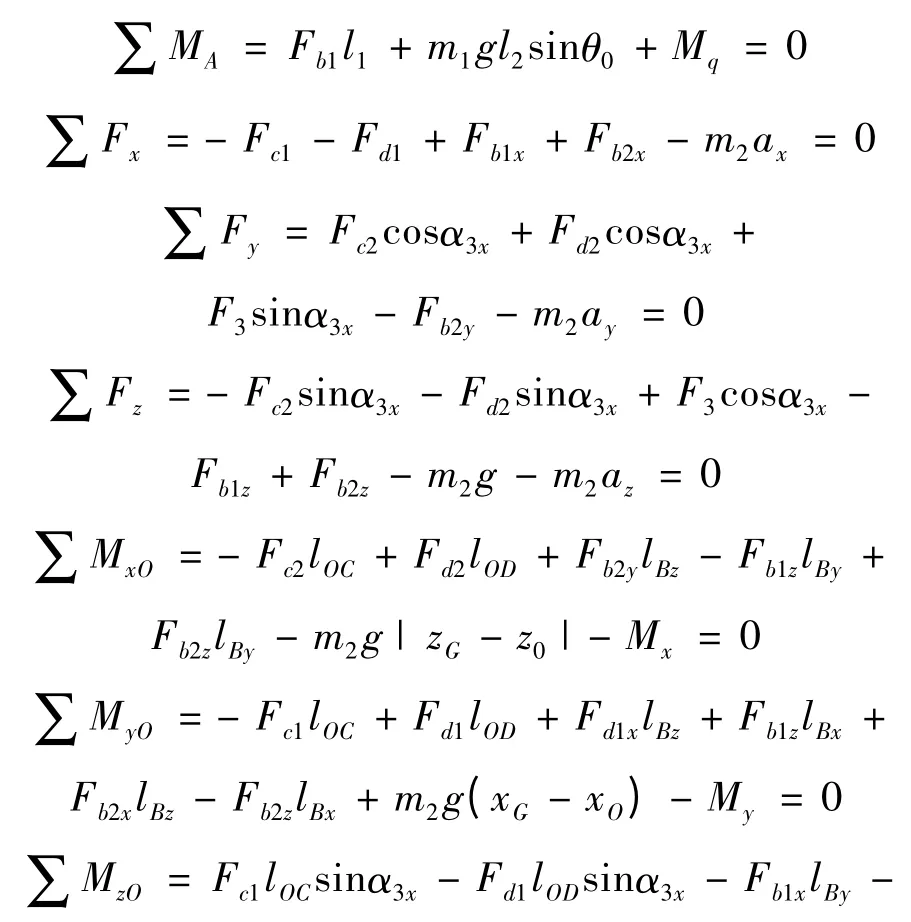
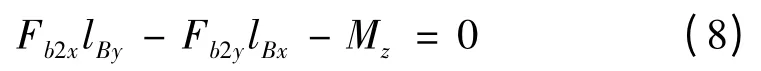
式中:Fb1x=-Fb1cosθ0,Fb1z=- Fb1sinθ0,Fb2x=-Fb2cosα01sinθ0,Fb2y=-Fb2sinα01,Fb2z=-Fb2cosα01cosθ0,lBx= lOBsinα01| sinθ0|,lBy= lOBcosα01,lBz= lOBsinα01|cosθ0|;ax,ay,az—坐标轴方向加速度,直接利用Adams 中的测量功能,可以测量这些值,其他尺寸及质量数值可由实际机构测得。
通过联立求解便能得到B、C、D 三处轴承力。在实际生产应用过程中,B 处轴承磨损较为严重,本研究着重分析该处受力变化。利用Matlab 软件计算得到受力变化曲线,与Adams 动力学仿真结果进行对比,设定电机转速为710 r/min,转动方向与图2 中θ0方向相同,运行时间为0.169 s。Fb1受力分析如图6 所示、Fb2受力分析如图7 所示。
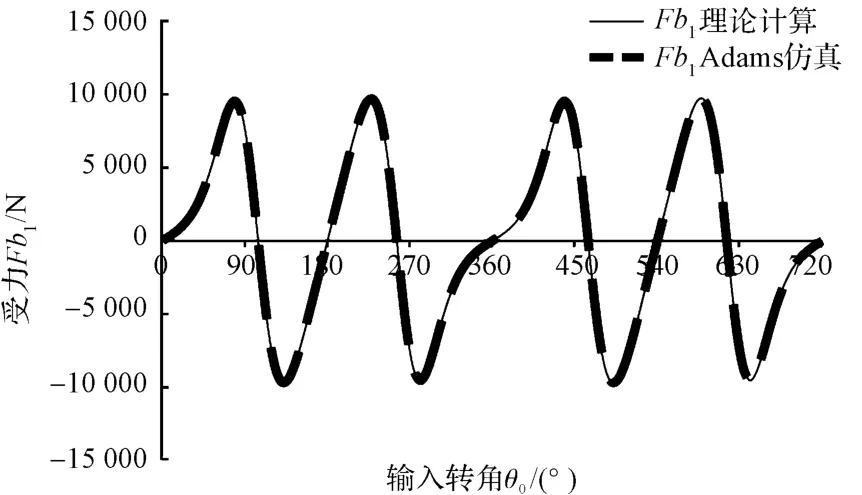
图6 Fb1受力分析
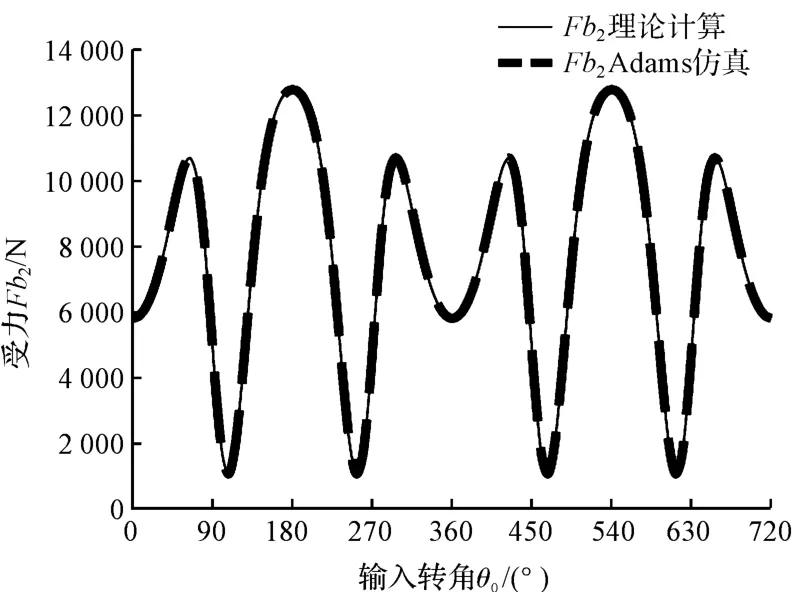
图7 Fb2受力分析
由图6、图7 可以看出,Adams 仿真与理论计算的结果相吻合,验证了公式推导的正确性,同时公式编程的优点在于,将各处载荷参数化,可对单一因素的影响进行分析。
结果显示,B 处轴承最大合力约为16 400 N,受力方向的周期变化易导致轴承损坏,同样可以得到其他各处轴承受力变化曲线的特性;700 r/min~800 r/min的转速在剑杆织机中属于高速运转;该GTM 型剑杆织机的门幅可扩至5 m 以上,考虑以上影响因素,选用合适的轴承应用于空间球面4R 机构中颇为重要。
5 结束语
本研究针对剑杆织机引纬机构中的空间4R 机构,从运动学和动力学两方面进行较完整地分析,使得其中做空间运动的叉形连杆的动能和惯性力矩有直接的理论表达式,对重要轴承处的轴向力、径向力进行计算,并利用Adams 软件仿真进行验证,方便轴承的选用,为今后学者深入研究球面4R 机构的运动、载荷等特性提供依据。同时发现α01,α12为该机构中极其重要的两个结构参数,影响球面4R 机构的空间构型,且α01对其影响程度较大,设计时可着重考虑,叉形连杆的两个分解摆动的极值表示了机构空间运动范围,有助于某些型号织机引纬部分中叉形连杆与十字节的配合设计,预防干涉;另外引纬机构箱体的造型也与其有关,通过控制箱体的体积有利于合理安排剑杆织机的占地空间。
[1]徐永康.空间四连杆引纬机构优化及动力学仿真[D].杭州:浙江理工大学机械与自动控制学院,2012.
[2]程起时,胡善义.空间四连杆传动的剑杆引纬机构[J].丝绸,2001(9):24-25.
[3]周香琴,张 雷.剑杆织机空间连杆引纬机构载荷特性研究[J].中国机械工程,2013,24(14):1881-1885.
[4]何士龙,王世恩.球面4R 机构的输入输出方程研究[J].科技情报开发与经济,2011,21(2):191-192.
[5]DAMIEN C,JORGE A. The computation of all 4R serial spherical wrists with an isotropic architecture[J].Journal of Mechanical Design,2003,125(2):275-280.
[6]张 雷,余克龙,陈少钟,等.基于ANSYS 和ADAMS 空间四连杆引纬机构的柔性动力学仿真[J].纺织学报,2013,34(5):116-120.
[7]张国柱,王惠刚.RSSR 空间四连杆机构的设计应用[J].纺织机械,2007(5):37-40.
[8]徐永康,张 雷. 基于Matlab 空间四连杆引纬机构运动仿真[J].轻工机械,2012,30(3):17-21.
[9]张启先.空间机构的分析与综合(上)[M].北京:机械工业出版社,1984.
[10]周香琴.球面4R 机构运动特性研究及其应用探索[J].中国机械工程,2011,22(2):153-158.
