飞轮储能系统轴系的优化设计研究*
2015-03-02徐登辉史涔溦黄晓艳
徐登辉,史涔溦 ,张 健,黄晓艳
(浙江大学电气工程学院,浙江杭州310027)
0 引 言
在能源与环境问题日益严峻的今天,对于储能方式的要求也不断提高。在多种多样的工况要求下,对电池的储能密度、体积、容量、质量、效率等均有了更高的要求。相较于传统的化学电池,飞轮储能系统采用将能量转化为旋转动能的方式进行能量储存,它具有储能密度大、功率密度大、效率高、低污染等特点[1]。在航空航天、电力系统调峰调压、车辆储能方面都有广泛的应用前景。飞轮储能的思想早在20 世纪中叶就有人提出过设想,不过限于当时材料强度,轴承技术以及充放电控制等因素,无法体现出其优势。直到20 世纪90年代,随着高强度的碳纤维,玻璃纤维等材料使得飞轮边缘线速度可达1 000 m/s,大大增加了飞轮储能的极限容量与储能密度;同时,随着半导体器件的普及与应用,电力电子装置不断升级,对于飞轮充放电的控制也提升到一个新的高度。随着磁悬浮、超导技术的发展,飞轮在高速下,支撑系统有了一个新的飞跃,配合真空技术,降低了摩擦损耗与风损,进一步提升了飞轮储能系统的效率[2]。
本研究对储能飞轮的材料边缘线速度、所受弯曲应力轴系的临界转速等方面进行研究。
1 飞轮系统设计
飞轮储能的基本原理是将电能转化为飞轮旋转的动能,使用时,将存储的动能转化为电能输出。飞轮储能设计储能量要求4 MJ,输出脉冲功率为200 kW,额定工作转速30 000 r/min。其储能量由动能公式(1)决定[3]:
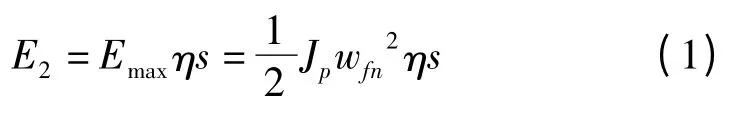
式中:Emax—飞轮总储能;Jp—转动惯量;wfn—飞轮额定旋转角速度;E2—输出能量;η—电机及变换电路效率,选取0.85;s—飞轮放电深度。
从式(1)可以看出,在放电机及变换电路效率和放电深度不变的情况下,提高飞轮储能量可以从增加转动惯量和提高转速两个方面着手,而相对于增加转动惯量,提高转速更加有效。然而,随着转速的上升,飞轮本体的结构强度将面临更加严苛的要求。故需要对飞轮结构尺寸进行设计优化,充分发挥各种材料的性能,调和转速和强度的矛盾,使得飞轮在能够满足储能需求的情况下,达到轻量化的目标。
笔者设计飞轮结构为圆柱形,对于空心圆柱形结构[4]:
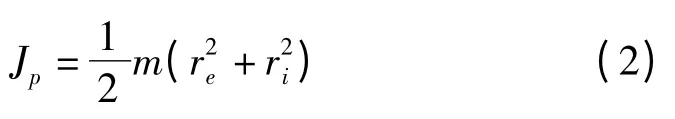
式中:m—空心圆柱质量,re—外半径,ri—内半径。将式(1,2)联立,得:
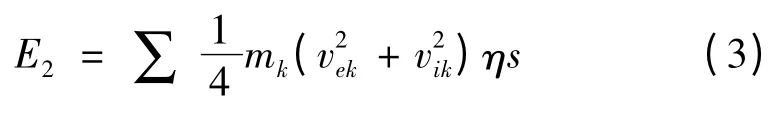
式中:mk—第k 层空心圆柱质量,vke—外环边缘线速度,vki—内环边缘线速度。
不同的材料会有其许用强度相对应的最大边缘线速度。根据式(3)可以看到在最大边缘线速度的约束下,质量越大,储能量越高。因而飞轮材料选用结构为:最内层轴采用强度较低而密度较高的调制合金钢;之后采用强度较高,密度也较高的钛合金材料;最外层采用强度最高但密度较低的碳纤维进行包绕。充分利用各部分的优势,提高储能效率。材料参数如表1 所示。

表1 各层材料主要参数
在相当长的待机时间里,飞轮转子需要保持高转速状态以存储能量,这就需要飞轮的支撑系统具有低摩擦低损耗的特点从而提高飞轮储能的效率。磁轴承是一种新型高性能轴承。与传统滚珠轴承、滑动轴承以及油膜轴承相比,磁轴承不存在机械接触,转子可以达到很高的运转速度,具有机械磨损小、能耗低、噪声小、寿命长、无需润滑、无油污染等优点,特别适用高速、真空、超净等特殊环境[5]。
飞轮系统采用立式结构,轮本体与额定转速转速30 000 r/min 的高速永磁同步电机同轴相连。上、下两端各采用一套刚度为1 MN/m 的径向主动电磁轴承固定,轴向采用永磁轴承卸载80%的重力,底端再辅以陶瓷轴承承载飞轮[6]。飞轮系统基本结构如图1所示。
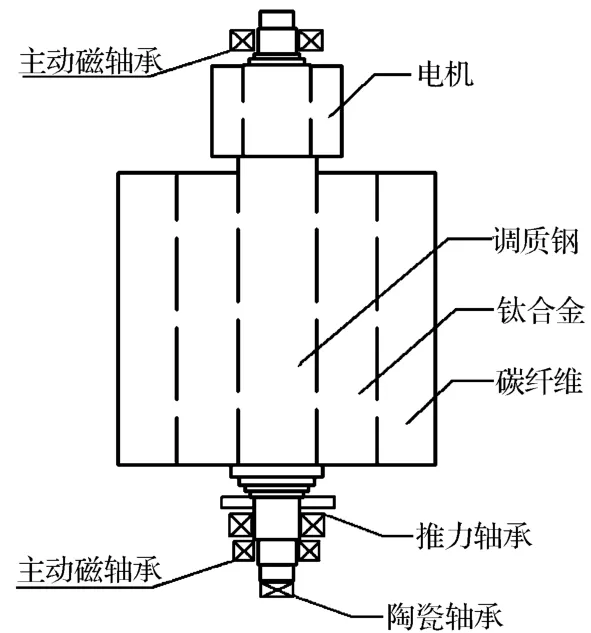
图1 飞轮储能系统简图
2 储能飞轮方案设计
2.1 储能量要求
在工作转速、储能量、放电深度、能量变换效率均确定的情况下,根据式(3),储能量要求转化为飞轮本体转动惯量的要求,进一步转化为对于飞轮整体高度,轴粗,钛合金轮环内外径,碳纤维轮环内外径的约束。
2.2 材料承受离心应力要求
对于各向同性的材料即钛合金与钢材料来说,飞轮高速旋转时,材料所承受最大离心应力为[7]:
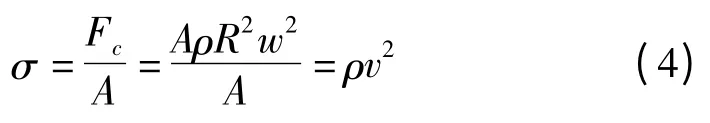
式中:σ—离心应力,Fc—离心力,A—截面积,ρ—材料密度,R—空心圆柱外半径,w—角速度,v—外边缘线速度。
本研究根据钢材料与钛合金材料的材料许用应力以及取适当的安全系数,最终确定在飞轮储能系统中,钢材料的边缘线速度不能大于200 m/s,钛合金材料的边缘线速度不能大于500 m/s。
对于各向异性的碳纤维来说,本研究采用厂家提供的600 m/s 的最大边缘线速度作为约束条件。
2.3 轴强度要求
而对于飞轮系统来说,在升速到工作转速过程中,会越过低阶的临界转速,对轴的强度要求进一步升高。这种情况转子属于挠性转子,本研究根据ISO1940 标准,选取精度等级G2.5,挠性转子的原始不平衡量偏心为刚性允许的剩余不平衡量偏心的10 倍,故取允许剩余不平衡度(不平衡偏心距)εper=0.8 g·mm/kg ×10 =8 g·mm/kg。
在工作中,轴系重心处受到径向拉力:

式中:Ft,m,ε,w—轴系重心处所受径向拉力,轴系质量,剩余不平衡矩,旋转角速度。
按许用弯曲应力计算进行校核[8]:
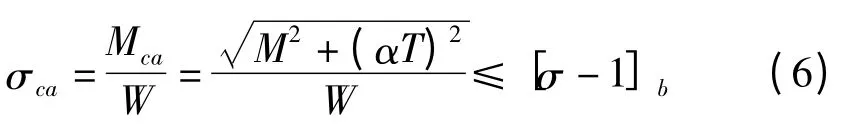
式中:σca—当量弯曲应力;Mca—当量弯矩;W—形状系数,对于实心圆柱来说W =πD3/32[8];M—合成弯矩,取重心处承受拉力乘以较长一段力臂;T—转矩;α—折算系数,按脉动循环应力计算取值为1;[σ-1]b—对称循环需用应力,Cr40 取值为70 MPa。
依据上述3 个要求,本研究设计一组飞轮储能系统轴系尺寸参数,具体标注如图2 所示。
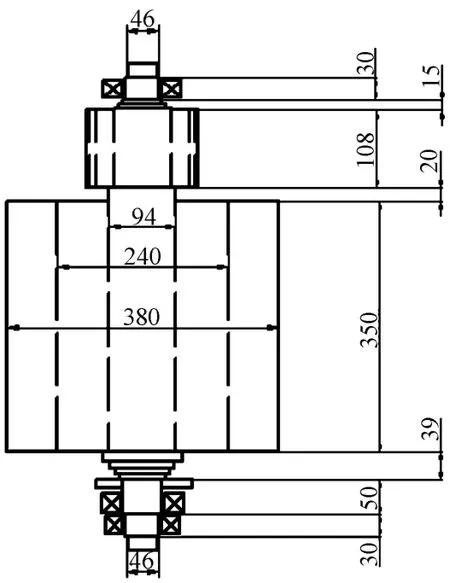
图2 飞轮储能轴系尺寸标注
2.4 临界转速要求
对于高速运行下的转轴来说,由于不平衡偏心、安装公差、轴承刚度等因素,质心会偏离形心,高速旋转下引起转轴弯曲,在转轴弹性恢复力的作用下会产生振动。通过进行模态分析,确定转轴的固有频率和振型,避免在工作转速范围内出现共振是十分重要的[9]。
高速旋转机械,对于在一阶临界转速以下工作的转子,应使工作转速n <0.75n1;对于在一阶临界转速以上工作的转子,应使工作转速满足1.4ni<n <0.7ni+1,其中:ni,ni+1—相邻两阶临界转速。本研究选取放电深度s=0.65,故工作转速要求在17 700 r/min~30 000 r/min之间。根据转速与频率的对应关系,工作频率在295 Hz~500 Hz,要求固有频率fi不允许存在200 Hz~700 Hz之间。
本研究在ANSYS Workbench 环境下对倒角与过度部分进行简化后建模,用modal 模块进行模态分析[10-11]。在主动电磁轴承处设置为刚度系数为1 MN/m。由于采用立式结构轴向扰动基本可以忽略,故本研究在永磁卸载轴承处设置柱形约束,将轴向位移约束为0。
仿真分析后得到的固有频率与振型结果如图3、图4 及表2 所示。

图3 飞轮储能轴系一阶弯振模态

图4 飞轮储能轴系二阶弯振模态
可以看到由于轴向采用的刚度较低的电磁轴承,前三阶模态为刚体模态;第二、三阶,第四、五阶,第七、八阶固有频率、振型相近,为振动方程重根,故可看作同一个模态。
由分析结果来看,在200~700 之间存在一阶弯振的情况,不能在实际的系统中使用,故需要对设计方案进行优化改进。

表2 轴系前7 阶模态固有频率与振型
3 飞轮参数优化设计
优化设计的方法有两种:
(1)解析法。通过求解微分方程和极值,进而求出最小值;
(2)数值方法。借助与计算机和有限元,利用多个数值点,采用样条差值的方法形成一条连续可用的函数表达曲线或曲面,来近似数学意义上的极值求解。通过反复迭代逼近,求解出最小值。
飞轮的形状寻优要考虑飞轮的转动惯量、质量、临界转速和飞轮内部的应力分布,用解析法计算十分困难,故本研究选取数值方法进行优化[12]。
对于电池而言,轻量化是极其重要的。就该案例来讲,在满足飞轮储能能量需求的情况下,质量最轻,也就意味着储能密度达到了最高。进一步如何选取各层材料的尺寸飞轮段的轴径,钛合金外径,碳纤维层外径,飞轮高度,使得满足工作要求的情况下质量最轻,成为本研究需要解决的问题。笔者根据上述问题得到优化设计模型。
(1)优化目标:
飞轮质量最小。
(2)优化参数:
飞轮段的轴径rs,钛合金外径rT,碳纤维层外径rC,飞轮高度h。
(3)约束条件:
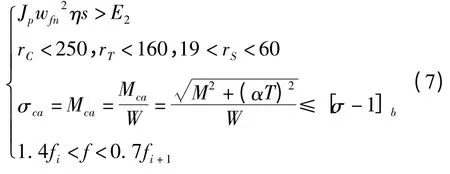
依次对应于出储能量约束,最大边缘线速度约束,转轴强度约束,临界转速约束。
本研究利用ANSYS Workbench 进行建模,采用Design Exploration 功能下的Goal Driven Optimization模块进行优化求解,为了获取更多的实验数据,便于构建响应参数曲面,笔者在Design of Experiments 中设置实验设计类型为Custom +Sampling,设置样本总量为200。参数中,设置飞轮段的轴径rS取值范围为45 mm~60 mm,钛合金外径rT取值范围为90 mm~160 mm 碳纤维层外径rC取值范围为160 mm~250 mm 飞轮高度取值范围为300 mm~500 mm。
本研究进行试验样本的仿真求解,同时生成了响应曲面,得到了各个优化参数对于受约束参数的贡献度。
最后在优化模块中,本研究对于优化目标以及约束条件进行设置,得到了软件根据响应曲面选取的3个备选点如表3 所示。其中的数据只给出了夹有工作转速下的两阶固有频率。

表3 优化后得到的3 组备选点数据
本研究从3 个备选方案中选取一个方案作为最终的优化设计方案。方案2 中,轴所受应力相对于其他两个方案有明显的上升,故淘汰方案2。3 个方案中方案1,3 比较相近,但方案1 对于优化目标-飞轮轻量化优势更明显。故本研究选取方案1 作为优化设计的最终方案。由于优化设计模块中给出的输出数据结果是通过响应曲面拟合获得的,并非有限元仿真结果,本研究要将备选方案回代入原模型计算。考虑实际的加工精度,笔者根据备选1 选取54,92,183,485 回代入原模型计算。
最后优化前、后数据对比如表4 所示。

表4 优化前、后参数对比
4 优化结果分析
本研究通过表4 中的数据对比可以看到,经过优化设计后,工作过程中转速不会跨域临界转速并留有一定的裕量;轴系所承受的最大弯曲应力减少了11.7%,储能量2.6%,质量增加1.3%,得到了满足工作要求的最轻量飞轮轴系尺寸参数。
5 结束语
本研究采用Workbench 有限元计算及目标驱动优化模块功能对影响飞轮储能运行因素进行了比较分析。笔者以飞轮本体尺寸参数为Workbench 输入参数,以飞轮材料强度、轴所受应力、飞轮储能量、轴系固有频率、飞轮本体质量为输出参数,选取飞轮本体质量最轻作为优化目标,进行了优化仿真。优化结果使飞轮固有频率合理地避开了飞轮运行的转速范围,满足飞轮储能系统储能量要求,轴系所受应力在材料需用应力范围之内,同时具有轻量化的特点。
与优化前相比,该优化方法保证了运行的可靠性,提高了材料性能利用率,提高了整机市场竞争力,为飞轮储能系统轻量化研究提供了参考依据。
[1]王江波.高速飞轮储能系统的研究与实现[J].电气传动,2014,44(1):26-30.
[2]蒋书运,卫海岗,沈祖培.飞轮储能技术研究的发展现状[J].太阳能学报,2000(4):427-433.
[3]李文超,沈祖培.复合材料飞轮结构与储能密度[J].太阳能学报,2001(1):96-101.
[4]张秀华,李光喜,王 琬.高速储能飞轮转子的分析与设计[J].煤矿机械,2012,33(6):57-59.
[5]王 健,戴兴建,李奕良.飞轮储能系统轴承技术研究新进展[J].机械工程师,2008(4):71-73.
[6]JIANG S,WANG H,WEN H. Flywheel energy storage system with a permanent magnet bearing and a pair of hybrid ceramic ball bearings[J]. Journal of Mechanical Science and Technology,2014,28(12):5043-5053.
[7]LIU H,JIANG J. Flywheel energy storage—An upswing technology for energy sustainability[J]. Energy & Buildings,2007,39(5):599-604.
[8]管胜荣.转子发动机偏心轴结构设计及强度校核[J].小型内燃机与摩托车,2010,39(3):48-51.
[9]唐长亮.20 kW/1 kWh 飞轮储能系统轴系动力学分析与试验研究[J].振动与冲击,2013(1):38-42.
[10]崔小龙,王泉中,蒋身学. 基于ANSYS 的机电产品包装箱底架模块分析与研究[J]. 包装与食品机械,2014(6):35-39.
[11]李文逸,宋以国,李 翀. 基于ANSYS 的复合材料飞轮系统模态分析[J].新技术新工艺,2012(4):4-6.
[12]郭振宇.基于差异演化算法的高速储能飞轮形状优化设计[J].吉林大学学报:工学版,2008(1):80-83.
