基于混合遗传算法的车间调度研究

冯世扣，鲍 敏 ，张 伟

(浙江理工大学机械与自动控制学院，浙江杭州310018)

0 引 言

生产车间调度是离散制造系统中关键的一个环节，车间调度通过合理分配现有的资源、安排零件加工次序和加工时间，能够有效的提高生产效率，对车间调度进行研究具有深远的意义［1-2］。生产车间调度问题种类繁多，本研究主要针对单件作业车间调度问题(job shop problem，JSP)。在用遗传算法求解JSP 问题时，初期种群之间差异非常大，很容易造成整个种群过早收敛，算法后期种群趋于一致，个体之间优势不明显，导致种群进化停滞不前［3-5］。为了使调度方案更实用高效，遗传算法得到不断改进和发展。Parviz Fatah［6］在求解过程中建立一个数学性规划模型，用启发式遗传算法结合模拟退火算法求解;张超勇［7］设计了一个种基于工序和机器编码的改进遗传算法，具有更好的遗传特性;王万良等［8］提出了改进自适应遗传算法，改进自适应遗传算法提高了获得最优解的速度;Victor 等［9］改进了混合遗传算法的交叉操作，并将改进的算法应用与车间调度问题中。

本研究针对遗传算法搜索效率低，易于过早收敛等缺点，提出一种新的混合遗传算法。这种算法核心在于:在每一代遗传进化过程中，引入退火思想，在迭代初期退火算法具有很高温度，此时算法有很强的概率突跳性，有利于打破过早收敛问题;引入自适应交叉和变异概率，能使算法在优化过程中自动改变交叉和变异概率，避免盲目交叉，从而提高搜索效率;设计新型的交叉和变异算子，以避免交叉后产生不可行解，相对于传统的算子新算子能够使种群更加的多样化，从而提高找到最优解的概率。

1 JSP 问题的数学模型

JSP 问题主要研究n 个工件(J1J2…Jn)在M 个机器(M1M2…Mn)上完成加工，每个工件有k 个工序，每个工序在不同的机器上完成，相应的完成时间也不同。JSP问题的目标就是通过优化工件在机器上的加工顺序，使加工完成的时间最短。通常JSP 问题有以下假设:

(1)不同工件的工序不存在先后顺序的约束。

(2)各个工序一开始加工就不能中断。

(3)每台机器可以加工不同工件的不同工序，但一台机器不能同时加工多种工序。

(4)每一个工件只有当前一个工序完成加工后，才能开始加工该工件后一道工序。

(5)每一个工序的加工时间和加工机器都是预先给定的。

JSP 问题的数学描述如下:

式(1)表示目标函数。式中:Cik—工件i 在机器k上的完成时间;n—工件数;m—机器数。

式(2)表示各工件的加工先后顺序。式中:cjk，tik—工件j 在机器k 上的完成时间和加工时间;M—一个足够大的正整数，如果工件j 比工件i 先在机器k 上加工，则xijk为1，反之为0。

式(3)表示工艺条件约束下各工件的加工顺序。其中:如果机器h 优先与机器k 加工工件i，则aijk为1，反之为0。

另外对一些符号作如下说明:

(1)加工时间矩阵T。T(i，j)表示加工第i 个工件的第j 个工序所用的时间。

(2)机器顺序矩阵J。J(i，j)表示加工第j 个工件的第j 个工序所用的机器号。

2 混合遗传算法的设计

在用混合遗传算法求解JSP 问题的过程中，关键步骤包括设计编码和解码方式、确定目标函数、设计遗传算子、确定遗传参数以及设计模拟退火过程等。

2．1 染色体编码

编码是遗传算法求解调度问题的关键，本研究采用基于工序的编码方式，该编码方式可以避免产生不可行解和死锁现象。当求解n 个工件在m 台机器上加工的问题时，染色体的基因数等于全部工序的数，为n·m 个。每一个工件的工序都用相应的工件号表示，第i 次出现的工件号就表示加工该工件的第i 道工序。如个体［2 3 1 2 3 1 1 2 3］表示3 个工件在3 台机器上加工，该染色体的加工顺序为工件2，工件3，工件1，工件2，工件3，工件1，工件1，工件2，工件3。

2．2 染色体解码

对于已有的染色体，结合机器顺序矩阵，可以得到加工所有工序的机器序号，从而得到一个有效的生产调度。

2．3 适应度值

适应度值用来衡量个体适应环境的能力，适应度值越大越优秀，遗传到下一代概率越大［9］。对于车间调度问题，适应度值是加工完成所有工件的时间Cmax的最小值。

式中:Cmax—加工完成所有工件的时间。

2．4 选择算子

选择算子是选择种群中高适应度值的个体进入下一代的操作。本研究采用比例选择方式，即被选中个体的概率正比与个体的适应度值:

式中:Pi—选择的概率，F(xi)—个体适应值。

2．5 交叉操作

种群通过交叉操作产生新个体，从而推动种群进化，因此交叉操作是最重要的操作。对于JSP 问题，笔者采用传统的交叉操作，产生的新染色体可能存在某个工序的多余或缺失，因此交叉操作的难点在于如何保证交叉产生的新染色体是可行解。本研究设计了基于工件序号的交叉操作，具体步骤如下:

步骤1:从父代中随机选择两个个体P1P2，随机产生两个不同的随机数i1和i2(0 ＜i1，i2＜n)，然后把P1P2中i1和i2都提取出来，保存在新的基因串A1A2中，并且保持这些基因相对位置不变，P1P2中相应的基因位置用0 来代替。

步骤2:然后把A2的基因插入到P1中基因为0 的位置，产生子代B1，把A1的基因插入到P2中基因为0的位置产生子代B2。

步骤3:把子代B1所有基因向左移动一位，子代B2向右移动一位，分别得到最终个体C1C2。例如:

P1为:

P2为:

A1为:［4 3 4 3 3 4］

A2为:［3 4 4 3 4 3］

P1为:［0 2 0 1 1 0 2 0 1 0 2 0］

P2为:［0 2 0 0 1 2 2 0 0 1 1 0］

B1为:［3 2 4 1 1 4 2 3 1 4 2 3］

B2为:［4 2 3 4 1 2 2 3 3 1 1 4］

C1为:［2 3 1 1 4 2 3 1 4 2 3 3］

C2为:［4 4 2 3 4 1 2 2 3 3 1 1］

通过以上交叉产生的个体不存在某个基因多余或缺失的情况，都是可行解。步骤3 中将子代向左向右移动，可以提高种群多样性，避免遗传算法早熟。

2．6 变异操作

种群通过变异操作，产生新个体，在保证种群多样性的同时推动种群向前进化。本研究中变异操作具体步骤如下:首先随机选择一个个体，随机产生两个位置，将两个位置之间的基因片段逆转，获得新的个体。例如P1为［4 2 3 1 1 4 2 3 1 3 2 4］，两个交叉位置Pose1和Pose2分别为4，9，则两个位置间的基因片段A1为:［1 1 4 2 3 1］，通过逆转A1，得到新片段A2为:［1 3 2 4 1 1］，最后用A2替换A1，得到子代B1为:［4 2 3 1 3 2 4 1 1 3 2 4］。

2．7 初始参数确定

在遗传算法中，交叉概率Pc和变异概率Pm会直接影响算法的收敛性。因此本研究对Pc和Pm进行重新的设计，Pc和Pm会随着适应度值变化而变化，具体如下:当个体的适应度值大于种群的平均适应度值时，该个体属于优良个体，应尽力保留，故Pc和Pm应该较小;反之，Pc和Pm应取较大的值。具体计算公式如下:

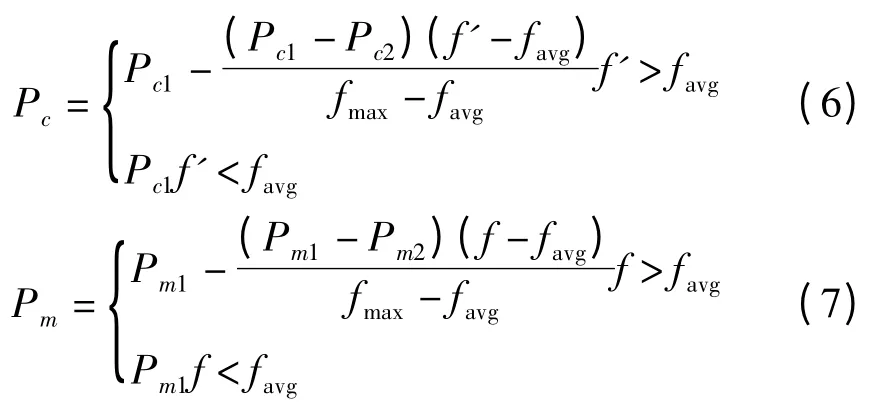
式(6～7)中:fmax—当代种群中最大适应度值，favg—当代种群适应度值的平均值，f'—两个交叉个体中较大个体的适应度值，f—要变异个体的适应度值。一般取Pc1=0．9，Pc2=0．6，Pm1=0．1，Pm2=0．001［10］。

2．8 模拟退火算法设计

本研究引入模拟退火算法中的Metropolis 接受准则使算法跳出局部最优解的“陷阱”。Metropolis 接受准则是以一定的概率P 来接受比原个体差的新个体，由该准则判断进过遗传算子的新个体是否替代父代个体，具体公式如下:

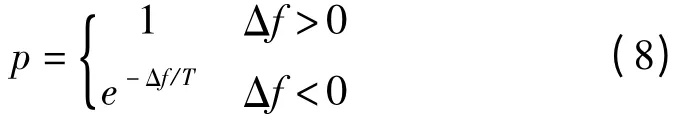
式中:T—模拟退火算法中的温度;Δf—经过遗传算子的新个体与原个体适应度值之差，若Δf 大于0，则接受适应值更高的新个体，否则产生一个［0，1］随机数b，若P ＞b，用新个体代替旧个体。

本研究给定初始温度T0，终止温度Tend，以及降温系数K，在每一次退温过程中，用Metropolis 接受准则决定最终的个体，直到达到温度达到Tend。

2．9 算法流程图

混合遗传算法流程图如图1 所示。

图1 算法流程图

3 仿真结果与分析

在混合遗传算法仿真实验中，笔者采用FT06 问题作为仿真案例［11］，即6 个工件，6 台机器的调度问题。机器的顺序矩阵J 和加工的时间矩阵T 如下所示:

Matlab 仿真试验中，采用的初始参数为Pc为0．9，Pm=0．1，Size=40，T0=10 000，Tend=0．1，K =0．9。用混合遗传算法得到最佳个体为［3 3 2 6 1 1 3 2 6 4 2 4 5 3 4 6 2 1 1 1 5 4 5 2 3 6 5 2 3 4 5 5 6 1 6 4］，需要的加工时间为55 s，达到该问题的最优解。算法收敛曲线如图2 所示，最佳个体的甘特图如图3 所示，即工件加工顺序图。

图2 收敛曲线图

为验证混合遗传算法的可行性，在同样的参数下，笔者分别用遗传算法和模拟退火算法求解FT06 问题，得到相应的结果，3 种算法的收敛曲线对比图如图4 所示。

从图2 中可以看到，混合遗传算法进过50 代完成了收敛，得到的最佳完工时间为55，与FT06 问题的最优解一致，表明混合算法具有一定的搜索精度和较高的效率。

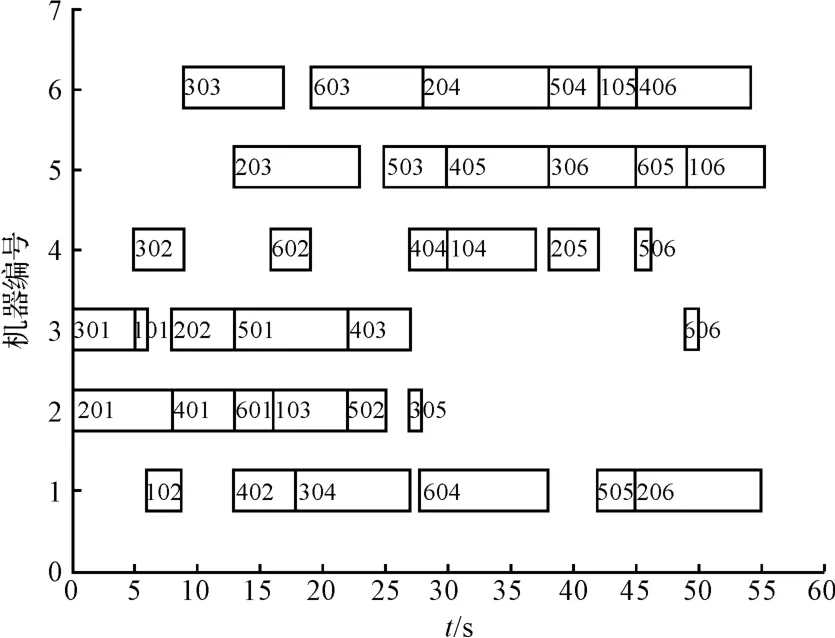
图3 生产顺序图

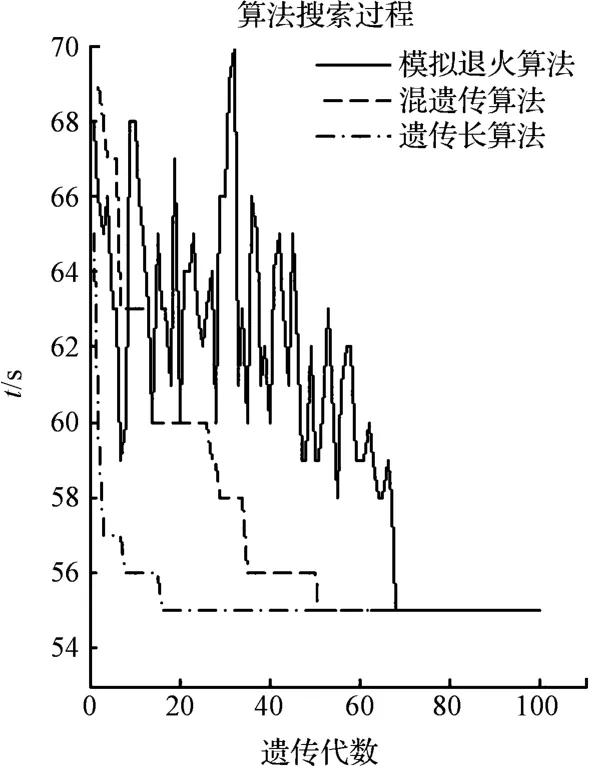
图4 3 种算法收敛对比图

从图3 中可以看到，每台机器加工工件的顺序，例如机器1 的加工工序顺序依次为工件1 第2 工序、工件4 第2 工序、工件3 第4 工序、工件6 第4 工序、第5工件第5 工序和第2 工件第5 工序。6 台机器上加工顺序包含了所有工件的所有工序，是一个完整的生产计划，也证明混合遗传算法编码方式避免了交叉和变异后产生非法个体。

3 种算法收敛曲线对比图如图4 所示。对比SA和GASA 曲线，可以看到SA 曲线前期有很大的波动，GASA 收敛更早，表明混合遗传算法能在全局进行搜索最优解，能够控制寻优方向，相对于SA 具有更快的搜索速度。对比GA 和GASA 曲线，可以看到GA 曲线前期收敛的非常快，在求解复杂问题时比较容易早熟，从而只求得局部解。GASA 曲线收敛较为平滑，能克服GA 容易早熟的缺点。

4 结束语

本研究描述了车间调度的数学模型，分析遗传算法在求解车间调度问题时存在的不足之处，重新设计基于工件编号的交叉算子和变异算子，优化了交叉和变异过程，同时采用自适应交叉和变异概率，避免遗传算法在迭代后期出现停滞不前的现状。同时笔者在优化过程中引入模拟退火算法，克服算法容易早熟的缺点。仿真结果显示混合遗传算法能够找到全局最优解，很好的解决JSP 调度问题。

本研究以产品的最小完工时间作为目标函数，找到了全局最优解，但实际生产过程中还应考虑客户满意度、生产成本、交货延期惩罚等其他指标，下一阶段应考虑多目标遗传算法的实现，提高算法实用性。

［1］邵新宇，饶运清．制造系统运行优化理论与方法［M］．北京:科学出版社，2010．

［2］王 凌．车间调度及其遗传算法［M］．北京:清华大学出版社，2003．

［3］吴 君，张京娟．采用遗传算法的多机自由飞行冲突解脱策略［J］．智能系统学报，2013，15(1):90-92．

［4］CHUN B T，LEE S H． An efficient workload redistrbution algorithm in grid computing systems using genetic information［J］．Convergence and Hybrid Information Technology Communications in Computer and Information Science，2012，310(2):164-171．

［5］ZHANG Jing-jie，XV Chong-hai，YI Ming-dong，et al． Design of nano composite ceramic tool and die material with back propagation neural network and genetic algorithms［J］．Journal of Materials Engineering and Performance，2012，21(4):463-470．

［6］FATTAHI P，MEHRABAD S M，JOLAI F． Mathematical modeling and heuristic approaches to flexible job shop scheduling problems［J］．Journal of Intelligent Manufacturing，2007(18):331-342．

［7］张超勇，饶运清，李培根．柔性作业车间调度问题的两级遗传算法［J］．机械工程学报，2007，43(7):119-124．

［8］王万良．人工智能及其应用［M］．北京:高等教育出版社，2008．

［9］YAURIMA V，BURTSEVA L，TECRNYJH A． Hybrid Flow Shop with Unrelated Machines Sequence Dependent Setup Time and Availability Constrain:an Enhanced Crossover Operator for a Genetic Algorithm［C］//Proceedings of the 7th international conference on Parallel processing and applied mathematics． Gdansk:［s．n．］，2007:608-617．

［10］王万良，吴启迪，宋 毅．求解作业车间调度问题的改进自适应遗传算法［J］． 系统工程理论与实践，2004，20(2):80-83．

［11］王 凌．智能优化算法及其应用［M］．北京:清华大学出版社，2001．