馈能型磁流变减振器的设计与仿真研究*

岳 旭 ，刘淑莲 ，杨礼康* ，孙海杰

(1．浙江工业大学机械工程学院，浙江杭州310014;2．浙江科技学院机械与汽车工程学院，浙江杭州310023)

0 引 言

磁流变液是一种智能材料，在外加磁场的作用下，它可瞬间(毫秒级)从牛顿流体转变为具有一定屈服剪切应力的非牛顿液体。磁流变减振器是应用磁流变液的新型智能减振器，相比于电流变减振器，它具有阻尼力可控、工作温度范围宽、响应快、功率消耗较低等优点，被广泛应用于汽车，工程建筑、桥梁、铁路、航空航天等领域的振动控制［1］。

磁流变减振器工作时需要外部电源为其提供励磁电流，产生控制磁流变液特性的磁场以调节阻尼力大小。在将磁流变减振器应用于实际工程领域振时，电源供给的中断会影响磁流变减振器工作的可靠性。因此需要考虑通过设计振动能收集装置来回收减振器在工作环境中的振动能，以摆脱其对外部电源的依赖。振动能收集方式主要有静电式、压电式、电磁式。静电式一般需要外部源设备工作，且发电能力弱，可用的场合很少。压电式虽然装置体积小，发电效率高，但总体产生的功率比较小，大多应用于无线传感和微机电系统等，不能给磁流变减振器提供足够的电能。

电磁式具有发电数值高，适应性强，因此国内外学者开始研究基于电磁式的馈能型磁流变减振器。马里兰大学的Choi 和Wereley［2］设计了一种馈能型磁流变减振器，将电磁感应发电装置集成在磁流变减振器的活塞上，整个装置体积较小，实现了振动能的收集目的，但是发电装置中永磁体会使磁流变液极化，缩小了磁流变减振器阻尼力的可控范围。香港大学陈超等人［3］设计了一种具有自感应速度的自供电磁流变减振器系统，相应的馈能装置早受振动驱动时产生的电能可满足磁流变减振器减振需求，但整个装置加工工艺要求较高;Bogdan［4-5］采用了永磁发电机作为振动能量采集装置，虽然解决了磁流变减振器系统的电能需求问题，但是该发电装置布置在磁流变减振器外部，很难推广应用。湖南大学汪志昊［6］是应用旋转式电磁感应发电装置为磁流变减振系统来供电，但为实现直线运动而引入了齿轮齿条转换结构，机械损耗比较大，发电效率不高。

本研究针对磁流变减振器需要外部供电限制其应用范围的问题，设计一种馈能型磁流变减振器，并对其进行研究与分析。

1 馈能型磁流变减振器工作原理

馈能型磁流变减振器结构示意如图1 所示。其主要由磁流变装置、馈能装置、电能管理模块及相关连接件构成，减振器底部法兰与馈能装置的外筒通过螺栓连接，中间连接杆将为馈能装置动子杆和减振器的活塞杆组成一个整体的运动部件。馈能装置的发电线圈与磁流变减振器励磁线圈通过导线连接在一起，电能管理电路对馈能装置产生的电能进行调节。

图1 馈能型磁流变减振系统结构示意图

由图1 可知馈能装置的外筒与磁流变减振器的缸筒通过法兰连接在一起，其定子凹槽内缠绕着发电线圈。振动时磁流变减振器的活塞杆在缸筒内做往复直线运动，带动动子杆上永磁体在相对定子做往复直线运动。由法拉第电磁感应定律可知，定子上的发电线圈内部的磁通量发生变化，从而产生感应电动势。由电能管理模块将产生的交流电转换之后控制磁流变减振器。

2 馈能型磁流变减振器设计

馈能型磁流变减振器可按功能分成3 个模块，即馈能模块= (馈能装置)、阻尼模块= (磁流变减振器)、电能管理模块=(全桥整流滤波电路)。性能好坏取决于这3 个模块的主要参数，本研究对其进行分析并计算。

2．1 磁流变减振器力学模型和结构设计

磁流变液力学特性可以采用Bingham 本构方程来进行描述:

式中:τ—剪切应力;τy—磁致屈服应力;η—动力粘度;—切应变率;sgn—符号函数，它表示活塞运动时的速度方向。

磁流变减振器用于减振装置，仅有剪切、流动和挤压3 种工作模式［7］，图1 中，磁流变减振器采用剪切和流动共同作用的混合模式结构示意如图2 所示。

在流动模式中，阻尼力的大小为F1:

图2 磁流变减振器结构示意图

在剪切模式中，阻尼力的大小为F2:

图2 中，混合模式的总阻尼力为:

其中:

式中:D3—活塞的直径，D1—活塞杆直径，l—阻尼通道长度，h—阻尼间隙，A—活塞端面有效作用面积，b—阻尼间隙等效宽度，v—活塞运动速度。其他符号同上文所示。

根据某汽车悬架在低频、小振幅(频率1 Hz～3 Hz、振幅10 mm)的振动产生的阻尼力范围为1 122 N～1 460 N［8］，为此笔者设计出磁流变减振器的主要结构参数如表1 所示。

表1 磁流变减振器主要结构参数

2．2 馈能模块数学模型及尺寸计算

2．2．1 馈能模块的数学模型

馈能装置的结构示意如图3 所示。该馈能装置主要包括定子、发电线圈、动子杆、永磁体以及背铁。定子凹槽有4 个发电线圈，通过反向串联形成单相绕组。背铁和圆环形永磁体固定在动子杆上，永磁体作为磁源，其充磁方向为轴向方向，相邻永磁体的充磁方向相反。定子和背铁所采用的材料是高导磁的硅钢材料，动子杆使用质量较轻的非导磁材料，永磁体为高磁性NdFeB35，发电线圈选取常规的漆包线。

图3 馈能装置内部结构示意图

2．2．2 馈能模型

在振动激励下，永磁体随动子杆往复运动，导致发电线圈内磁通量发生变化产生感应电动势。当发电线圈没有和外部负载相连处于开路状态时，定子凹槽内第i 个线圈产生感应电动势可以表示为［9］:

式中:Ei—第i 个发电线圈产生的感应电动势，Ψi—发电线圈i 中由永磁体产生的磁链，z—动子杆运动位移，v—动子杆运动速度。

由于永磁体和发电线圈之间是相对直线运动，Ψi可以表示成:

式中:Ni—发电线圈i 的匝数，φg—轴向方向气隙内的磁通量，τ—馈能装置的磁极距，θi—发电线圈i 的相位角。

联立式(5，6)可得:

假设第一个发电线圈产生的感应电动势的相位角为0°，由于相邻发电线圈的相位角相差180°，相邻发电线圈产生的感应电动势大小相等、方向相反，通过将4 个发电线圈反向串联构成一个单相绕组，则可以使4个发电线圈产生的感应电动势方向和大小都相同，设4 个发电线圈的匝数为N，得到馈能装置感应电动势E 为:

当馈能装置中发电线圈与外部负载即活塞励磁线圈相连时，馈能装置向外输出的电能可以表示为:

式中:P—馈能装置输出功率，R—发电线圈的电阻，R1—活塞励磁线圈的电阻。

由式(9)可知在一定振动速度下，馈能模块的永磁体确定后，发电线圈匝数是影响馈能装置输出功率的主要因素，需分析计算。

2．2．3 发电线圈匝数分析

发电线圈匝数及相应电阻与漆包线直径之间的关系为:

式中:ρ—漆包线的电阻率，κ—发电线圈充满系数，h4—发电线圈轴向长度，d5—发电线圈的外径，d4—发电线圈的内径，wd—漆包线的直径。

式(10，11)表明:发电线圈电阻和匝数成正比，增大发电线圈匝数则必然致电阻增大。因此需要优选匝数和线圈电阻，以便在一定条件下，使输出功率最大。

本研究基于低频、小振幅(频率1 Hz～3 Hz、振幅10 mm)的振动场合，考察阻尼模块输出最大阻尼力对应馈能模块产生的电能值大小，选取在振幅10 mm，最大频率3 Hz 的振动条件下，观察其发电线圈匝数对馈能装置输出电能的影响，从而选取合适的发电线圈匝数。下面通过仿真分析得到发电线圈匝数与馈能装置输出电能的变化曲线如图4 所示。

图4 中，当发电线圈匝数N 由720 增加到1 140的过程中，随着发电线圈匝数的增加，馈能装置输出的电压和电流也随之增大。当线圈匝数由1 140 增至3 216的过程中，输出电压和电流随着线圈匝数的增加都呈下降的趋势。在发电线圈匝数为1 140 时，馈能装置输出最大电压和电流分别为5．73 V 和1．62 A，其理论上输出的最大电能为9．28 W。

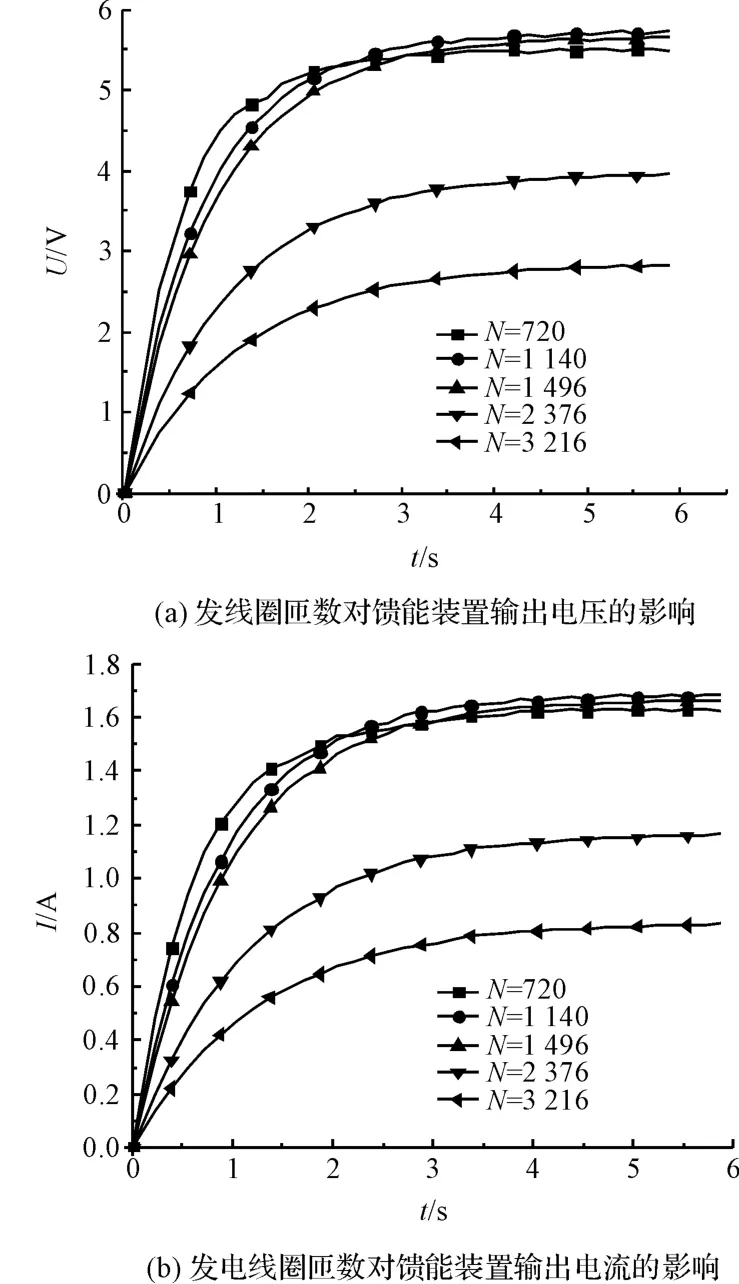
图4 发电线圈对馈能装置输出电能的影响

仿真结果表明，馈能装置输出电能的效率与发电线圈的匝数有关。发电线圈匝数过少则直接影响馈能装置的发电能力;发电线圈匝数过多，尽管馈能装置产生的电能多，但是由于其内阻较大，输出的电能大部分消耗在内阻上，从而使负载获得的电能减少。因此，本研究通过仿真比较分析，选取发电线圈匝数为1 140，此时，输出功率最大。

馈能装置的根据在低频、小振幅(频率1 Hz～3 Hz、振幅10 mm)的振动下，馈能装置输出电能能够满足磁流变减振器在某汽车悬架减振功能，设计的馈能装置主要结构尺寸如表2 所示。

表2 馈能装置的主要结构尺寸

(续表)

2．3 电能管理模块电路

根据馈能装置收集的电压特点及相关结构参数，本研究设计的全桥整流滤波电路如图5 所示，该电路由一个桥式整流电路和一个存储电容组成。桥式整流电路可以将方向不断改变的感应电动势转换成方向不变的直流电压，通过存储电容充、放电功能可以使馈能装置输出稳压直流电，满足磁流变减振器工作需求。

图5 全桥整流滤波电路

3 馈能型磁流变减振器仿真分析

本研究应用所确定的发电模块和阻尼模块的结构参数，分析整体性能特性。

3．1 基于Ansoft 的馈能特性仿真分析

本研究应用表2 给出的馈能装置主要结构参数进行Ansoft 电磁场仿真分析，其回馈电压和电流如图6所示。可以看出随着振动的频率的增大，回馈的电压和电流也随之增大。振动频率为1 Hz 时，输出电压和电流分别为1．64 V 和0．50 A;振动频率为2 Hz 时，输出的电压和电流分别为3．62 V 和1．07 A;振动频率为3 Hz 时，输出的电压和电流分别为5．73 V 和1．62 A。在频率1 Hz～3 Hz、振幅10 mm 的振动条件下，馈能装置输出的电能范围为0．82 W～9．28 W。

3．2 基于Simulink 的磁流变减振器的阻尼力仿真分析

馈能模块给阻尼模块提供的电能范围为0．82 W～9．28 W，本研究采用Lord 公司生产的MRF140CG 磁流变液［10］，应用表1 给出的磁流变减振器结构参数，根据公式(5)建立的仿真框图如图7 所示。

图6 低频、小振幅条件下回馈电能情况

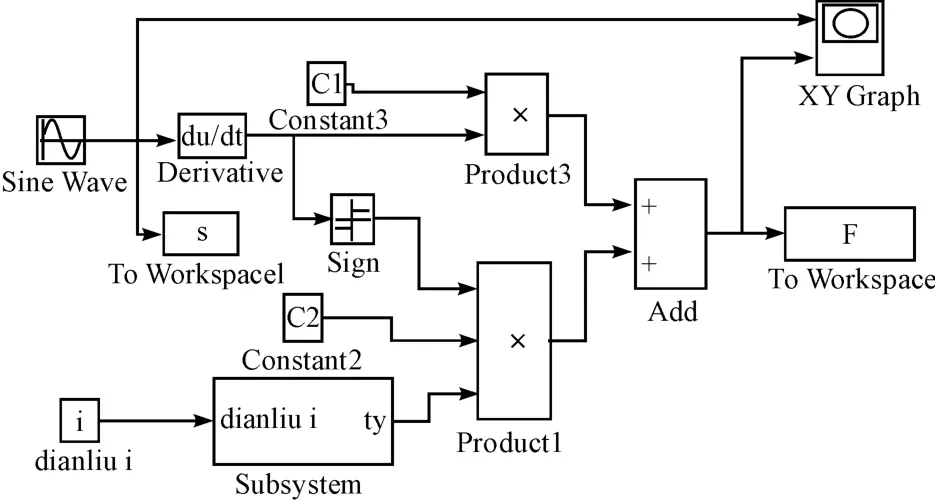
图7 磁流变减振器阻尼力仿真模型

仿真所得磁流变减振器的阻尼力-位移如图8所示。

从图8 中可知，随着振动频率的不断增加，磁流变减振器输出的阻尼力也逐渐增大。振动频率1 Hz、2 Hz、3 Hz 时，所对应的阻尼力分别为1 072 N、1 685 N、2 028 N。

以上仿真分析说明，所设定的振动条件下，发电模块提供的电能使阻尼模块可产生的阻尼力在1 072 N～2 028 N 范围内变化，能够满足馈能型磁流变减振器的减振性能要求。

图8 磁流变减振器的阻尼力-位移曲线

4 结束语

针对集成式馈能型磁流变减振器，本研究探讨了其阻尼、馈能结构设计方法，并通过馈能装置输出电能的数学模型，分析了选取其发电线圈匝数和建模合理选取了其发电线圈匝数负载。

在设定条件下，仿真结果表明，发电模块提供的电能可使阻尼模块产生1 072 N～2 028 N 的阻尼力，能够实现在低频、小振幅条件下对阻尼力的调节作用。整体上，说明本研究中该馈能型磁流变减振器设计方法的可行性。

［1］姚 春，梅德庆．用于汽车悬架的磁流变减震器研究综述［J］．机电工程，2006，23(1):58-62．

［2］CHOI Y T，WERELEY N M． Self-powered magnetorheological dampers［J］． Journal of Vibration and Acoustics，2009，131(4):44-46．

［3］CHEN C，LIAO W H． A self-powered，Self-sensing Magnetorheological Damper［C］//Proceedings of the 2010 IEEE．International Conference on Mechatronica and Automation．New York:［s．n．］，2010:1364-1369．

［4］SNAMINA J，SAPINSKI B． Energy balance in self-powered MR damper-based vibration reduction system［J］． Bulletin of the Polish Academy of Sciences Technical Sciences，2011，59(1):75-80．

［5］SAPINSKI B，SNAMINA J，JASTRZEBSKI L． Laboratory stand for testing self-powered vibration reduction systems［J］． Journal of Theoretical and Applied Mechanics，2011，49(4):1169-1181．

［6］汪志昊，陈政清．基于振动能量回收的自供电MR 阻尼器集成与试验研究［J］．振动与冲击，2013，32(12):88-94．

［7］赵 银． 新型结构磁流变减震器的的设计与仿真研究［D］．湘潭:湘潭大学机械工程学院，2011．

［8］王 勘．集成永磁直线发电机的汽车自供电磁流变减振器研究［D］．重庆:重庆大学机械工程学院，2013．

［9］蒋学争，胡红生，王 炅．基于电磁感应能量捕获技术的磁流变阻尼器研究［J］． 振动与冲击，2012，31(13):11-15．

［10］蒋学争．自供能磁流变阻尼器的振动能量捕获技术研究［D］．南京:南京理工大学机械工程学院，2012．