基于频谱分析的负荷形态分类研究

杨震男，袁 飞，杨 凯，卢 毅

（东南大学 电气工程学院，南京 210096）

随着电力市场的不断发展，电力需求侧管理技术的应用也愈加广泛[1]。由于我国电力市场还不够完善，目前主要是通过鼓励用户节电、提高能源利用效率以及有序用电管理的方式推广电力需求侧管理。相较于过去拉闸限电的强制措施，现在的有序用电决策方案结合电力用户自身的用电特点使其更加的人性化、环境友好化[2]。而高效可靠的负荷形态分类是准确进行负荷预测及合理制定有序用电决策方案的基础[3]。研究电力系统负荷形态分类的方法旨在研究电力系统负荷的构成，从而合理确定各类用户的典型负荷曲线，这对进一步研究负荷预测及有序用电调度问题有至关重要的作用。

电力系统负荷形态分类方法多样，以分类数目合理、同类负荷相似度高为目标，使各类负荷特性曲线更具代表性。目前将频域分析应用到电力系统负荷形态分类的方法还很少，而时域分析方法的缺点在于其将原始负荷序列作为一个整体，无法从中区分出不同的周期变量，因此也无法有效地量化描述负荷曲线的峰谷波动特性及其变化趋势。可见时域分析方法难以全面评估电力负荷峰谷特性，对电力负荷形态分类有一定的局限性[4]，这将在1.2节中详细阐述。

本文将频谱分析应用于电力系统负荷形态分类研究之中，通过分析基波分量的波动特性有效观察负荷曲线的波动实质。引入了频谱分析的波动分布因数和频率分布率作为负荷序列的特征值，使电力负荷的峰谷波动特性更加凸显。考虑电力系统负荷的波动特性使得电力系统负荷形态分类更加高效可靠，有益于安排电力用户错避峰及合理轮休等有序用电计划。

1 基于频谱分析的负荷形态分类方法

随着需求响应进程的加快，智能配电网中大规模新能源的接入和工业结构与经济状况的快速变化，使得电力负荷的时变性逐渐增强。传统电力负荷特性分类方法大都集中在时域上对电力用户负荷序列提取特征值（特征向量）再进行聚类分析[5]。由此衍生出的聚类方法也很多，但基于时域分析的负荷形态分类方法其提取的特征值，如：负载因数、峰谷差因数等，难以全面评估电力负荷峰谷特性。本文针对电力负荷特性时域分析的不足，将对电力负荷特性的研究从时域转变到频域。基于频域分析的电力系统负荷形态分类示意图如图1所示。

基于频谱分析的负荷形态分类步骤上与传统时域负荷形态分类相比多出了频谱分析环节，因而计算选取特征向量环节也不同于时域上的负荷形态分类，这将在下文叙述。

1.1 数据预处理

电力系统中负荷研究都是基于原始数据的，要使负荷研究的结果可靠就必须通过去除坏数据与归一化的步骤。去除坏数据是将原始数据中“不良数据”和“坏数据”剔除，归一化是将负荷数据除以最大值以消除过大数值范围的数据量级差对结果造成的影响。

1.2 频谱分析

图1 负荷特性分析示意图

频谱分析的方法有很多，如：WELCH法、多窗口法（MTM）、多重信号分类法（MUSIC），以及最大熵法（MEM）等。最大熵法自1980年以来以其高分辨率和短时性的特点逐渐得到广泛的应用[6]，故算例采用最大熵法（MEM）对日负荷序列做频谱分析。

最大熵法即为最大熵谱分析，其基本思想是对所测量的有限个数据以外的数据不做任何确定的假设，而是在熵信息为最大的前提下将未知的相关函数用迭代的方法递推出来。对应于每个频率ω的自回归谱密度用式（1）计算

式中：αk、δω分别表示p阶AR自回归模型系数的最小均方误差，回归模型参数满足以下线性方程

式中：测量数据序列xi(i=1,2,…,N)的自相关函数为

并且具有性质

下面选取2组电力系统负荷数据进行频谱分析，并作为算例说明传统时域分析方法的不足。电力系统负荷归一化数据及其功率谱密度值如表1和表2所示，其对应的负荷数据的时域和频域曲线图如图2、图3所示。

表1 电力用户负荷归一化数据

图3 电力系统负荷频域曲线

表2 电力用户负荷功率谱密度

图2 电力系统负荷时域曲线

从图2中可以明显地看出：A负荷与B负荷的负荷高峰、低谷时刻相近，且2个负荷的峰谷差也基本相同，通过时域分析方法易得出2个负荷的峰谷特性相似的结论，因而A、B负荷理所当然被分为同一聚类中。但当考虑电力负荷的波动特性后结论就大不一样了。由于电力负荷序列存在周期波动特性，这本身就很适合运用频域分析法。在频域分析里可以得到影响波动最大的基波周期分量，可以分析负荷特性，比较不同负荷曲线。同样是对A、B负荷进行特性分析，当采用频域分析法时便得到了图3。由图3可以看出，A负荷在较低频率处的周期分量较大，而在其它频率的分量很小；相反，B负荷在较高频率的周期分量较大，而在其它频率的分量较小。这意味着A负荷的长周期分量占很大比重，峰谷波动特性更显著；而B负荷的短周期分量占较大比重，峰谷波动特性不明显。可见频域分析法解释了电力负荷的波动特质，在负荷曲线波动问题的研究上有其独特的优势。

目前需求响应尚在深入研究中，随着智能电网和经济发展的推进，电力负荷也更加趋于复杂，传统的负荷特性时域分析方法难以适应新的电力环境，也很难全面有效的反映电力负荷峰谷波动特性。而电力负荷的频域分析方法有效地弥补了时域分析方法在表现负荷波动特性方面的不足，为研究准确高效的电力负荷聚类方法奠定了基础。

1.3 计算选取特征向量

电力负荷特性常表征为负荷特性指数，如负载因数和峰谷差因数等，这些指数能够部分的描述负荷曲线的峰谷特性，反映电力系统的运行状态，但电力系统还需要有指数来描述电力系统的波动特性。

为了获得电力系统负荷形态的聚类分析结果，首先要选定各个负荷的特征值（特征向量），根据负荷特征值（特征向量）的不同将其具有相似特征的负荷分为一类。

对负荷序列进行频谱分析后得到了电力系统负荷功率谱密度，基于功率谱密度数据，引入2个频域参数，即波动分布因数FD及频率分布率FR。波动分布因数FD指任意2个相邻频率振幅乘积的均方差除以其平均值，FD值越大表明负荷序列能量分布越集中。频率分布率FR表示每一频带中频谱密度均值占均值总和的百分比，即各频带频谱密度分布。FR值在低频带时较大表明负荷时序的长周期分量比例较高，负荷曲线波动特性更明显；相反，FR值在高频带较大时表明负荷时序短周期分量比例较高，负荷曲线波动特性较小。从而，基于频域分析的负荷形态分类时选取取特征向量为

式中：Sfeat表示频域上选取的特征向量；FD表示负荷功率谱的波动分布因数；FR表示负荷功率谱的频率分布率。

以1.2节中选取的负荷数据为例，计算基于频域上负荷形态分类时的特征向量如下。

根据示例表2中电力系统负荷的频域数据易得

式中：Psdi=psdi·psdi+1为相邻频率点谱密度乘积；为其平均值；Ⅱ、Ⅲ、Ⅳ）为对应第I个频带中的谱密度平均值。

从而频域上选取的特征向量应为

传统时域分析时特征值及特征向量选取不同于上述频域分析时特征值及特征向量的选取，其通常是由时域负荷数据直接求得，如选取负荷序列的日峰谷差率（Peak/Valley Ratio）、日负荷率（Load Ratio）、峰谷时段负荷率（LR of Peak/Valley Hours）等作为负荷的特征值。容易看出，电力负荷的传统时域分析方法中特征值的选取使得原始数据的相当一部分信息丢失，仅通过日峰谷差率、日负荷率、峰谷时段负荷率等参数难以全面有效地评估负荷数据的波动特性。

1.4 动态聚类分析

所谓聚类，即将分类对象看作是多维空间里的向量，按照空间关系的远近将具有相似属性的事物聚为一类。

几种常见的聚类分析法有系统聚类、动态聚类、神经网络聚类等，无论采用哪种聚类，必须先确定样本的特征向量，从而确定不同样本之间的相似性，而距离即是度量样本或变量之间相似性的工具。设xij（i=1，2，…，n；j=1，2，…，p）为第i个样本的第j个特征值。定义dij为样本Xi=（xi1，xi2，…，xip）T与Xj=（xj1，xj2，…，xjp）T的距离。常用的距离定义有明氏距离、马氏距离、兰氏距离和斜交空间距离等。算例采用明氏距离中的欧式距离，其定义为

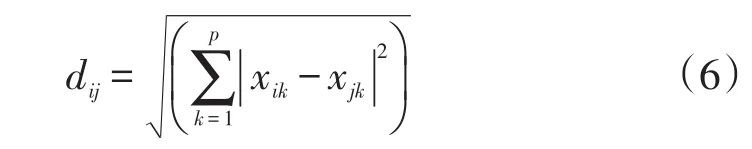
动态聚类分析法是基于样本相似性度量的间接聚类方法[7]。该方法与系统聚类法相比有以下优点：

（1）在聚类过程中，样品的属性可以发生改变。

（2）当样品数较大时，计算量较小，占用的内存空间较少。

其中K均值聚类算法是典型的动态聚类分析算法。假定待分类样本的特征向量集为该方法取定K类及K个初始聚类中心，按照最小距离原将样本分为K类，然后修正K个聚类中心并调整样本分类直到各样本到其所属类别的中心距离之和最小。算法步骤如下：

·任选K个样本特征向量为初始聚类中心，记作

·将待分类样本特征向量集{Xi}中的样本逐个按最小距离原则分配到某一类，即若则判定式中：表示Xi和的中心的距离，上角标是迭代次数，第k次迭代后产生新的聚类

·计算新聚类的聚类中心

式中：为类中样本的个数。计算新聚类中心的方法即是计算各新聚类中所有样本的重心。

·若新产生的聚类和前一次聚类结果一致则结束，否则重复第2步骤。

K均值聚类算法需要预先确定分类数及选定初始聚类中心，聚类结果使其各聚类样本离中心距离平方和最小。但初值的选定对结果有较大影响，不同初值聚类结果不尽相同。

1.5 聚类有效性评价

算例采用聚类综合质量Ocq（ξ）来衡量不同聚类的有效性[8]。Ocq（ξ）指数包含2部分内容，即聚类密集性指数Cmp和聚类邻近性指数Prox。聚类密集性是衡量聚类内方差的指数，方差越小则数据的统一性越高。给定总样本X，则聚类内方差定义为

式中：d(xi-)是矢量xi与X中心之间的距离；N为样本X的总个数。对聚类结果c1，c2，…，cC，聚类密集性定义为

式中：C为聚类个数，var(ci)是聚类ci的方差。Cmp值越小则聚类密集性越好。

聚类邻近性的定义为

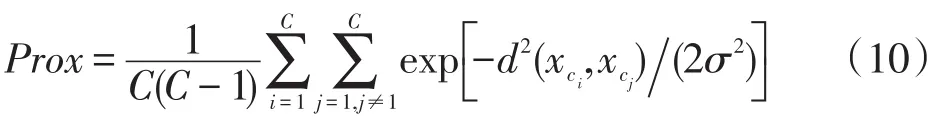
式中：σ为高斯常数，取2σ2=1以简化计算；xci是聚类ci的中心；d（xci，xcj）是聚类ci中心与cj中心之间的距离。Prox值越小即各聚类间越有效的分开，聚类效果越好。

为了综合评价某个聚类系统的聚类质量，将上述聚类密集性和聚类邻近性组合，即得到了聚类综合质量指数Ocq

式中：ξ∈[0 ,1]，是平衡聚类密集性与聚类邻近性的权值的参数，本文取ξ=0.5即权值相等。显然，聚类综合质量指数越大聚类效果越好。

2 算例分析

算例选取实际测量得到的47个用户平均日负荷序列作为待分类样本[9]，负荷数据均为工作日数据。对所有用户负荷进行编号，即负荷1至负荷47，预给定负荷聚类数为6类。聚类分析结果如表3所示。

根据聚类结果将同一类负荷的负荷曲线画在同一坐标内，并将各聚类用户的平均负荷曲线用红色粗实线标示于图中，如图4、图5所示，图4为时域分析聚类结果，图5为频域分析聚类结果。

图4、图5中曲线给人以直观的认识，可近似看出哪些聚类的统一性高以及各聚类的特点。但感性认识不一定可靠，聚类有效性需要一个理性的评估。分别对2种聚类结果进行综合聚类有效性评估后得出的数据如表4所示。

通过表4数据可知，基于频谱分析的聚类在聚类邻近性Prox、聚类密集性Cmp及综合聚类有效性Ocq3项指标上均要优于基于时域的传统聚类。在较为完备的Ocq聚类有效性评价体系中每个指标的优化都十分难得，算例获得如表4的优化结果足见基于频谱分析的聚类方法相较于传统时域分析的聚类方法而言有一定优势。

表3 基于时域和频谱分析的聚类结果对比

图4 基于时域的聚类分析结果

图5 基于频谱分析的聚类结果

表4 2种聚类结果综合聚类有效性评价指数对比

3 结论

基于电力系统用户负荷序列对用户进行分类需要负控技术的不断完善，更需要负荷分类方法的科学有效。本文针对传统时域分析聚类方法的不足将频谱分析与动态聚类分析相结合，得到了基于频谱分析的负荷形态分类方法。结合算例，将基于时域的传统聚类与基于频谱分析的聚类算法相比较，结果表明，基于频域分析的负荷聚类方法有更高的综合聚类有效性。该方法为电力公司准确进行负荷预测及制定有序用电决策方案打下坚实基础。

[1]王明俊.市场环境下的负荷管理和需求侧管理[J].电网技术，2005，29（5）：1-5.

[2]王蓓蓓，李扬，高赐威.智能电网框架下的需求侧管理展望与思考[J].电力系统自动化，2009，33（20）：17-22.

[3]张忠华.电力系统负荷分类研究[D].天津：天津大学，2007.

[4]Yu Cheng,Nan Dong.Research on spectral analysis method of load characteristics in smart grid[C]//Fuzzy Systems and Knowledge Discovery(FSKD),2011 Eighth International Conference on.IEEE,2011,4:2 561-2 565.

[5]杨浩，张磊，何潜，等.基于自适应模糊C均值算法的电力负荷分类研究[J].电力系统保护与控制，2010（16）：111-115.

[6]聂士忠，王玉泰.最大熵谱分析方法和MATLAB中对短记录资料的谱分析[J].山东师范大学学报：自然科学版，2005（3）：40-41.

[7]徐艺萍.动态聚类法研究[D].重庆：西南大学，2006.

[8]杨燕，靳蕃，Mohamed Kamel.聚类有效性评价综述[J].计算机应用研究，2008，25（6）：1 630-1 632.

[9]朱晓清.电力负荷的分类方法及其应用[D].广州：华南理工大学，2012.