实用基准负荷法的比较研究
2015-03-02苗晓峰陈云龙程婷婷
苗晓峰,张 利,陈云龙,程婷婷
(1.电网智能化调度与控制教育部重点实验室(山东大学),济南 250061;2.国网山东省电力公司 电力科学研究院,济南 250061)
1 背景
随着智能电网的发展,电力需求侧管理在提高电网运行效率,保证电网安全、稳定运行方面发挥着越来越重要的作用[1]。电力用户基准负荷作为评估需求侧管理的一种重要手段,被广泛的采用。通过计算电力用户基准负荷与实际负荷的差值,即可得到电力用户在参与需求侧管理过程中负荷的实际削减/转移量。因此,电力用户基准负荷的准确计算,对于需求侧管理的评估具有重要的意义。
电力用户基准负荷的计算方法主要分为2类:基于统计学原理的基准计算[2—8]和基于回归分析的基准计算[9—11]。基于统计学原理的计算方法,主要通过计算所选取的历史负荷数据的平均值来得到预测基准负荷,其值往往要比实际负荷偏低。因此,为了更好的反映事件日当天各因素(如:气温)对负荷造成的影响,需对预测基准负荷进行调整,调整系数可通过将事件时刻前几小时的负荷数据和预测基准负荷同时段的负荷相比较求得。基于回归分析的基准负荷计算,以电力用户的历史负荷数据为基础,建立电力用户的负荷与各影响因素(如:气温)之间的关系。采用线性回归模型时,由于实际中各影响因素难以完全分析清楚且它们与负荷间也并非线性关系,因此计算精度有待提高;而过于复杂的非线性回归模型虽可提高精度但不利于工程实践。同时,回归分析方法需要大量的历史负荷数据,过多的数据收集与处理也是造成其不便于工程应用的重要原因。
鉴于基于统计学原理计算方法简单、可操作性强的特点,它在工程实际中得到了较好的应用。美国多个电力市场实施了各自的实用基准负荷方法,这些方法经多年应用,积累了丰富的经验,但效果仍未完全满意。因此,文献[12]提出,在计算电力用户的基准负荷时给历史负荷数据设定权值,使越靠近事件日的历史负荷数据具有越大的权值,从而提高了在一些气候变化较大或者负荷变化较大情况下的计算精度。随着我国对有序用电[13]工作的进一步重视,各方面的理论研究有待开展[14—16],探讨实用的基准负荷方法也是亟待解决的问题。
本文立足于工程计算问题,在对上述实用方法进行详细探讨的基础上,以山东省某地区矿物制品业中的2类用户为例,进行了各方法的仿真计算,并基于对结果和误差的分析比较,总结了每种方法在应用上的优缺点及提高计算精度的改进方向。
2 基准负荷法
基准负荷是指在没有实施任何需求侧管理措施的情况下电力用户的负荷。通过将实际负荷与基准负荷对比,即可确定各种需求侧管理措施的实施效果,如图1所示。
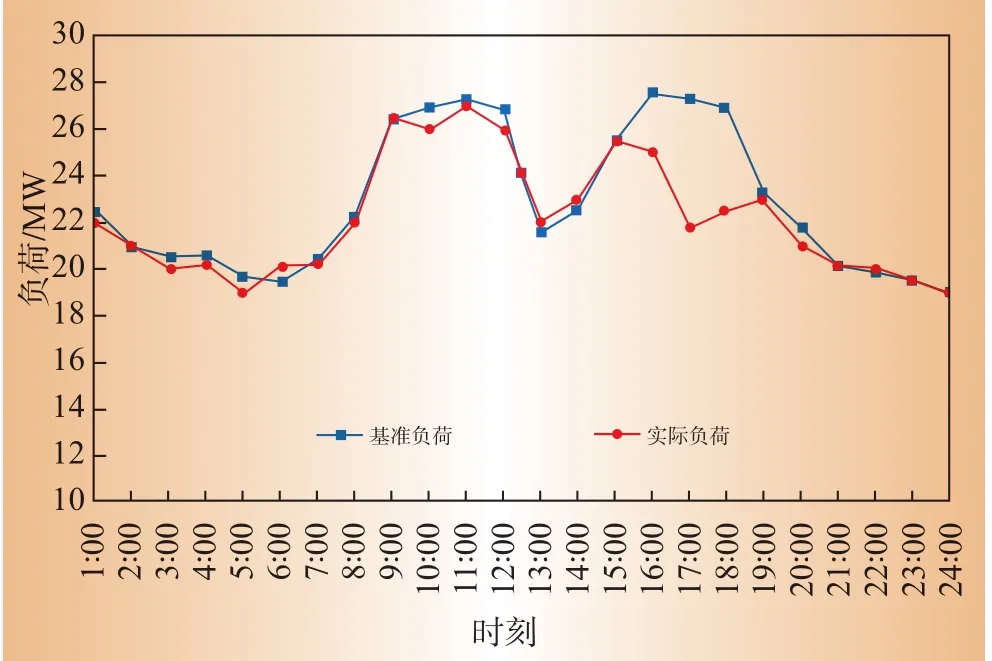
图1 实施需求侧管理措施后负荷的变化
基准负荷值与电力用户实际负荷测量值的差值即为电力用户的负荷削减/转移量,因而准确的计算基准负荷是评估需求侧管理措施的关键。考虑电力用户负荷固有的波动性和不确定性,因此为尽可能的实现准确的计算,基准负荷计算方法需要满足以下几点要求:
(1)准确性:即基准负荷值与电力用户实际负荷的差值要尽可能等于电力用户的真实削减值,避免仅从电力用户的报装容量来计算负荷削减而带来的误差。
(2)完整性:计算结果应全面的反映电力用户负荷曲线的整体特性,避免受电力用户故意增加用电等不合理用电行为的影响。
(3)可操作性:基准的计算方法应该简便易行,这将更有利于政策的透明化,方便电网公司和电力客户应用。
(4)适用性:方法应满足电网公司不同需求侧管理目标的计算需要,可方便地根据实际情况进行基准的调整,以更真实的反映电力用户的负荷情况。
合适的基准负荷计算方法应在平衡这4点要求的基础上进行选择。
3 各种算法的探讨
实施需求侧管理的日期本文称为事件日,记为T。预测基准负荷(predicted baseline load,PBL)通过计算事件日T前n-m+1天各天负荷L(T-i)的平均值来得到,如公式(1)所示
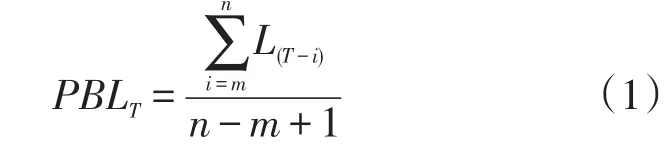
以工作日基准负荷计算为例,表1示意了m=1、n=10时的历史数据的选取,其中斜体日期表示事件日;灰色背景表示数据采集日,其选取不包括节日、周末、事件日。

表1 基准负荷计算所需历史数据列表
前n-m+1天的数据可以全部采用,也可以仅采用其中负荷较高的x天的负荷数据。考虑到实施需求侧管理的目的在于负荷高峰时期引导用户合理的安排用电,选取负荷较高的几天来计算基准负荷可以有效的减少预测值较低的现象,从而使计算结果更接近实际。
考虑事件日当天各因素对用户负荷的影响,将有助于提高计算精度,因此需要据此对预测基准负荷进行调整。设aT,t为调整系数,用来调整预测基准负荷。以事件时刻t前一定时段(定义为调整时段)的测量负荷C(时刻t-b到t-e间的负荷)来确定。调整策略分为加法调整和乘法调整,系数的计算方法分别如公式(2)、公式(3)所示
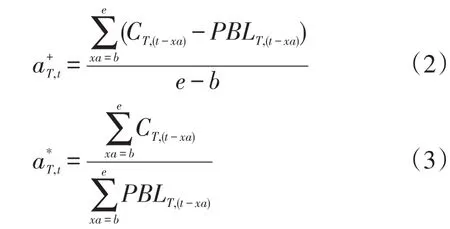
、分别表示事件日T事件时刻t时的加法和乘法调整系数。关于调整时段的选择,可根据所实施需求侧管理措施的具体特点,排除事件时刻t前两三个小时来确定。
预测基准负荷PBL通过加法或者乘法调整后,所得结果称为用户基准负荷CBL。加法调整和乘法调整分别如公式(4)、公式(5)所示
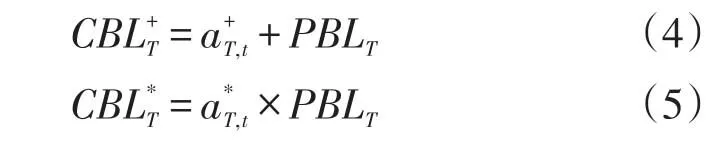
由此,实施需求侧管理期间用户的负荷变化就可以由公式(6)计算得到
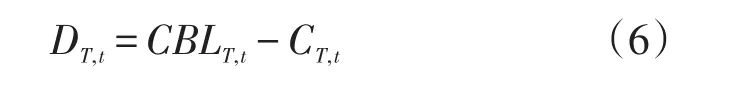
DT,t大于 0 时,表示t时刻负荷削减;DT,t小于 0时,表示t时刻负荷增加。
基于上述分析,对文献[2]—文献[8]中采用的工作日基准负荷计算方法进行了归纳总结,各方法的原理基本相同,如公式(1)—公式(5)所示,不同点在于数据采集日、调整时段以及调整系数的选择,如表2所示。
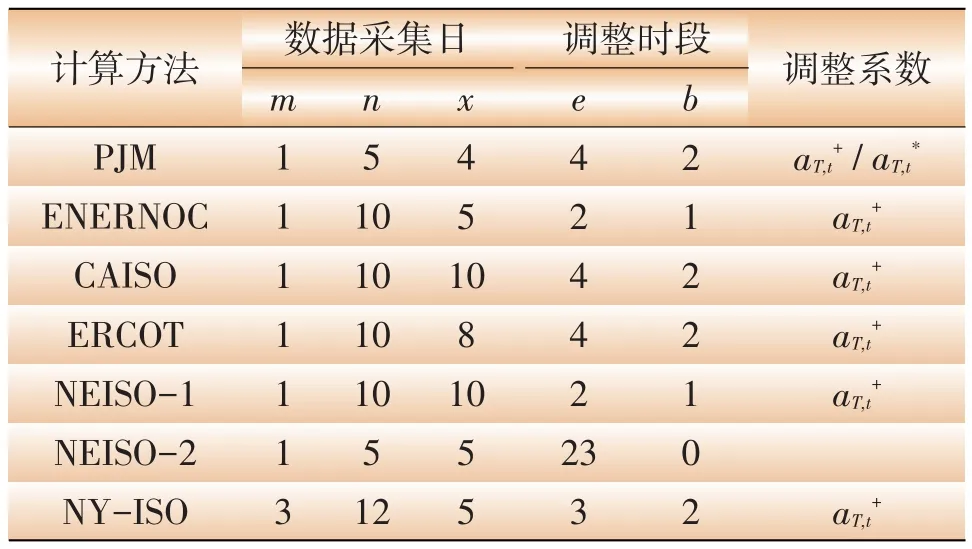
表2 各种基准负荷计算方法
说明:
(1)因为工作日与非工作日的负荷性质有很大不同,而且工作日负荷更高,实施需求侧管理措施的概率更大,因此计算基准负荷所需数据不包括周末、节假日以及事件日的负荷数据。
(2)乘法调整系数的取值范围为[0.8~1.2]。
(3)新英格兰电力市场有2种不同的方法,区别表示为NEISO-1和NEISO-2。其中,NEISO-1方法所用数据中排除了与预测基准负荷有25%偏差的负荷数据;NEISO-2方法的基准负荷由90%的预测基准负荷与10%事件日负荷(含事件时刻负荷)组成。
(4)ERCOT方法排除最高和最低日负荷,采用余下8天的数据。
(5)ENERNOC方法调整系数按照公式(7)进行计算
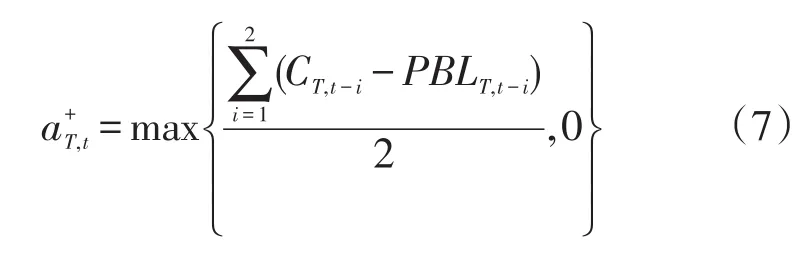
上述各计算方法本质上都是通过求取历史数据的平均值来得到基准负荷,但也各具特点。
从历史数据窗口的长度看,PJM和NEISO-2方法是5天,其余方法是10天。根据计算原理,较短的时间窗口不利于平抑近期负荷波动,适当的增加历史负荷数据的窗口长度,可以降低近期负荷波动的影响。但时间窗口的选择也并不是越长越好,因为过长的时间窗口会掩盖负荷近期变动的趋势。
从数据筛选机制看,CAISO,NEISO-1,NEISO-2方法不对历史数据进行筛选;PJM方法是剔除负荷最低的一天;ERCOT方法则是剔除最高和最低负荷;ENERNOC和NY-ISO方法是选取10天中负荷最高的5天。鉴于需求响应措施一般作用于高峰负荷时刻,因此适当的进行数据筛选可以有效地避免基准负荷计算值偏低。
调整时段与调整系数的选择体现了计算方法中对实施需求响应措施前实际负荷与历史负荷之间差异的考虑。在特定的需求响应项目中,措施实施前往往需要提前通知用户,因而一些方法如PJM,CAISO,ERCOT,NYSIO等在计算调整系数时避开了提前通知时间,从而减小了用户刻意在措施实施前提高负荷等投机行为的影响。在没有电力用户投机的情况下,则选取越靠近事件时刻的负荷值,越能更好的反映负荷的变化趋势。
4 仿真分析
本节基于电力用户实测数据对上述表2中的7种方法进行仿真计算,并通过对计算结果进行对比分析,总结了各方法的特点。
4.1 仿真数据
仿真数据选取为山东省某地区矿物制品业中2类用户2011年8月的负荷数据,为行业用户每小时的总负荷数据。2类用户由于实施不同的电价政策因此有不同的负荷特点,其8月平均日负荷曲线如图2所示。这样可便于比较各方法在不同负荷特性下的计算精度。
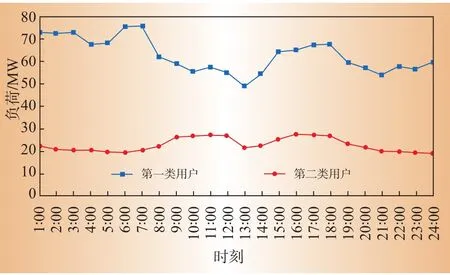
图2 平均日负荷曲线
为清楚起见,图3、图4给出了8月15日—8月19日,8月22日—8月26日,8月29日—8月31日各日13:00~17:00的负荷数据,以便更好的反映事件时刻和调整时段中负荷的变化趋势。需求侧管理措施的实施主要发生在负荷高峰日,因而本文选取数据集中负荷最高的31日作为事件日进行仿真计算,事件时刻设为17:00。
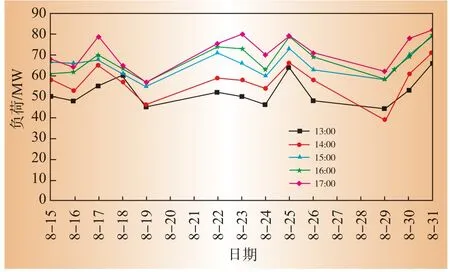
图3 第一类电力用户的历史负荷数据
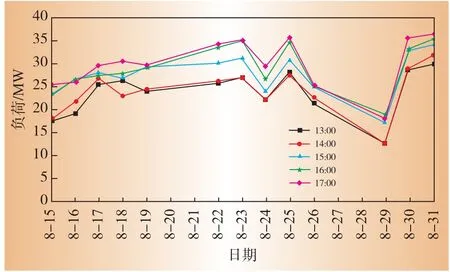
图4 第二类电力用户的历史负荷数据
以山东省为例,实施需求侧管理主要发生在工作日,因而周末、节假日的数据参考意义较低,本文对其进行了排除。
4.2 结果分析
各方法的计算结果见表3。表中PJM+和PJM*分别代表采用加法调整和乘法调整的PJM方法,1和2分别代表第一类电力用户和第二类电力用户,加法调整系数的单位为MW,乘法调整系数无量纲。在不同负荷特性下,各方法的计算误差见图5。
由图5可以看出:无论对于第一类还是第二类用户,误差最大的计算方法都为NEISO-2方法,说明它在不同的负荷特性下都不能得到满意的结果,不宜采用。没有进行数据筛选,同时将事件时刻的负荷值纳入了修正计算(此时电力用户已进行负荷削减),是该方法会产生较大负误差的主要原因。
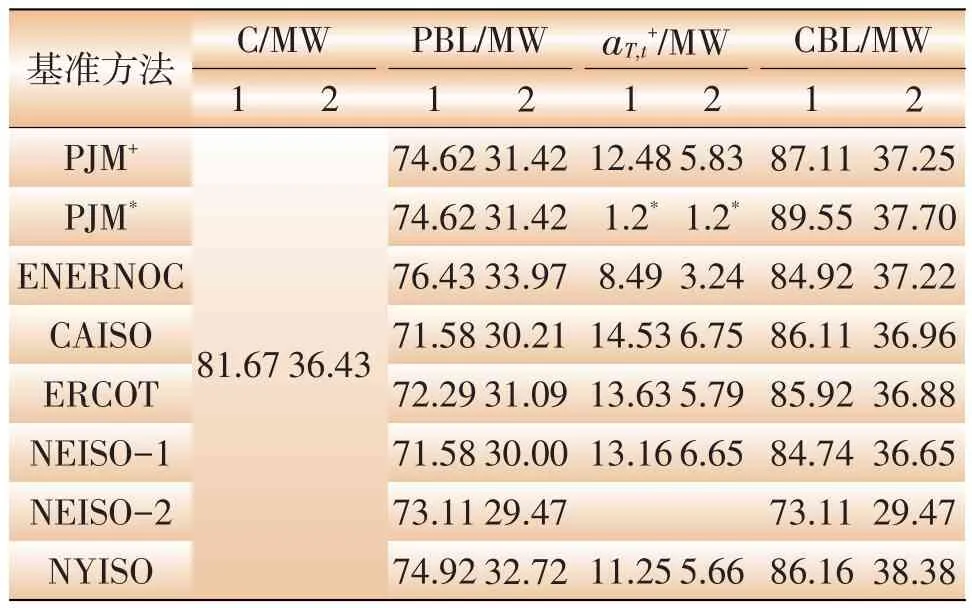
表3 各基准方法计算结果
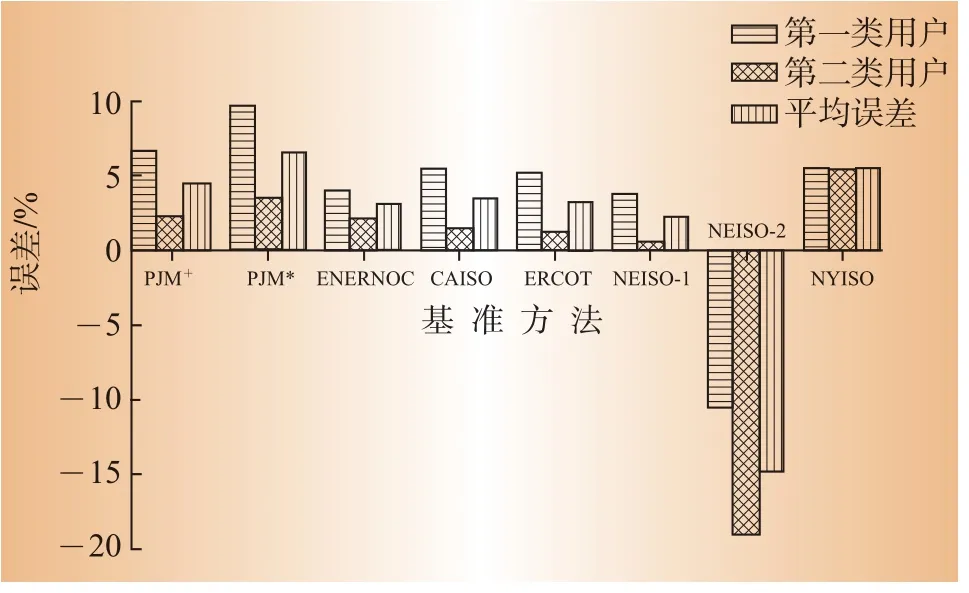
图5 不同负荷特性下各基准方法的计算误差
4.2.1 各方法计算效果
(1)各方法在同一负荷特性下计算精度不同。对第一类电力用户,PJM*方法计算误差绝对值最大,为9.64%;NEISO-1方法计算误差绝对值最小,为3.76%。对第二类电力用户,NY-ISO方法计算误差绝对值最大,为5.37%,NEISO-1方法误差绝对值最小,为0.61%。由图3、图4可见,本文算例的2类用户事件时刻(17:00)和事件前一时刻(16:00)的负荷规律都比较一致,因此充分考虑紧邻事件时刻负荷进行调整的NEISO-1方法有最好的表现,而采用乘法调整系数的PJM*方法,以及调整时段较远离事实时刻的NY-ISO方法,未能很好的把握2类用户的特征,导致较大的误差。
(2)同一种方法在不同负荷特性下其计算精度也不同。如PJM*方法,针对第一类电力用户其计算误差为9.64%,而对于第二类电力用户其计算误差仅为3.5%,图3、图4可以看出,在负荷历史数据窗口内,第二类电力用户各日负荷的规律一致性较第一类电力用户强,因而应用乘法调整系数会有比第一类电力用户更好的计算效果。
(3)ENERNOC、NEISO-1等方法的计算误差和平均误差都在5%以内,说明这2种方法对不同负荷特性的适应性较强。而PJM+、CAISO、ERCOT等方法虽然平均误差也在5%以内,但在不同的负荷特性下其计算精度相差很大。从方法的计算原理来看,调整阶段的选择是造成如此差别的主要原因。对本文算例而言,ENERNOC和NEISO-1方法都很好地利用了紧邻事件时刻的负荷数据,从而计算效果更好。若在NEISO-1方法中采用与CASIO方法相同的调整时段,则对第一类用户其误差就由0.61%变为1.45%,对第二类用户其误差由3.76%变为5.43%。其他方法都是利用距事件时刻较早的数据进行基准的调整,因而计算结果的偏差有所增大。
合适的基准负荷计算方法应在平衡准确性、完整性、可操作性以及适用性这4点要求的基础上进行选择。
4.2.2 提高基准负荷计算精度的改进方向
(1)准确性。本文所选取的数据为电力用户每小时负荷数据,可能因小时内负荷的变化过大而产生较大的计算误差。如果采用每15 min或者每5 min的负荷数据,电力用户负荷变动的概率大为减小,计算精度会进一步的提高。另外,选取计算所用历史数据时,如果尽可能选取相似日的负荷数据,即历史负荷的规律与事件日负荷的规律最大限度的保持一致,则会更有利于计算精度的提高。
(2)完整性。为避免受电力用户在事件时刻前故意增加用电从而多获补偿的不合理用电行为影响,应在算法中增设负荷限值的检测。如:对实施需求侧管理期间的电力用户负荷值异常变动进行检查,从而抑制电力用户不合理用电行为的发生,并有效减少其影响。
(3)可操作性。为保证方法的计算精度,应对采集的历史负荷数据是否能够反映事件日电力用户的负荷规律进行判别。对此,可采用文献[12]提出的方法给各历史数据设置权值。
(4)适用性。在基准负荷的计算过程中,应反映环境气候、行业政策等对电力用户负荷的影响,文中讨论的各方法利用事件时刻前的数据对预测基准负荷进行修正,虽一定程度上反映了各因素的影响,但针对极端气候天气或者用户受行业政策影响负荷变化较大的情况时,应予以额外的调整。
5 结论
基准负荷法在需求侧管理措施实施效果评估中发挥着重要作用,是准确评估电力用户负荷削减/转移量的有效手段。本文对已有的基准负荷法进行了详细的分析探讨与仿真计算,可得出如下结论:
(1)由于采用的数据集和调整方法不同,各方在同一负荷特性下计算精度不同。
(2)在不同负荷特性下,同一方法的计算精度不同。
(3)合理选择调整时段的方法具有最好的计算精度和平均精度。
可见,合适的基准负荷方法的选择应就需求侧管理措施实施的具体情况进行具体分析。
最后,本文从基准负荷计算方法应满足的准确性、完整性、可操作性以及适用性这4点要求出发,对如何进一步提高方法的计算精度给出了改进的方向。
[1]王蓓蓓,李扬,高赐威.智能电网框架下的需求侧管理展望与思考[J].电力系统自动化,2009,33(20):17-22.
[2]ENERNOC.The demand response baseline[EB/OL].[2008-10-01].http://www.naesb.org/pdf4/dsmee100608enernoc_2.pdf.
[3]PJM.Amended and Restated Operating Agreement of PJM Interconnection,L.L.C.[EB/OL].[2013-01-17].http://pjm.com/~/media/documents/agreements/oa.ashx.
[4]J Pedersen,California ISO.Proxy Demand Resources Full Market Module[EB/OL].[2011-01-01].http://www.caiso.com/275d/275d778249a30.pdf.
[5]ERCOT.EmergencyInterruptibleLoadServiceDefaultBaselineMethodologies[EB/OL].[2011-03-02].http://www.ercot.com/content/services/programs/load/eils/keydocs/Default_Baseline_Methodologies_REVISEDFINAL.doc.
[6]NE-ISO.Demand Response ISO New England Markets[EB/OL].[2010-06-01].http://www.isone.com/support/training/courses/wem101/16_demand_resources_in_new_mkts.pdf.
[7]NYISO.Manual 5:Day-Ahead Demand Response Program Manual[EB/OL].http://www.nyiso.com/public/webdocs/documents/manuals/planning/dadrp_mnl.pdf.July 2003.
[8]Antunes P,Faria P,Vale Z.Consumers Performance Evaluation of the Participation in Demand Response Programs Using Baseline Methods[C]//PowerTech(POWERTECH),2013 IEEE Grenoble.IEEE,2013:1-6.
[9]Yamaguchi N,Han J,Ghatikar G,et al.Regression Models for Demand Reduction based on Cluster Analysis of Load Profiles[C]//Sustainable Alternative Energy(SAE),2009 IEEEPES/IASConference on.IEEE,2009:1-7.
[10]Grimm C.Evaluating baselines for demand response programs[C/OL].http://publications.aeic.in/lrc/12_Evaluating_Baselines_for_Demand_Response_Programs_PA PER.pdf.
[11]Mathieu J L,Callaway D S,Kiliccote S.Variability in automated responses of commercial buildings and industrial facilities to dynamic electricity prices[J].Energy and Buildings,2011,43(12):3 322-3 330.
[12]Wi Y M,Kim J H,Joo S K,et al.Customer Baseline Loa(CBL)Calculation using Exponential Smoothing Model with Weather Adjustment[C]//Transmission&Instribution Conference&Exposition:Asia and Pacific 2009.IEEE,2009:1-4.
[13]国家发展和改革委员会.有序用电管理办法[L].2011.
[14]王志伟,薛亮,张国庆,等.山东省有序用电智能决策系统设计及应用[J].电力需求侧管理,2011,13(6):52-54.
[15]高赐威,李倩玉,宋宏坤.基于用电权交易的有序用电新机制[J].电力需求侧管理,2013,15(3):5-10.
[16]李正明,张纪华,陈敏洁.基于层次分析法的企业有序用电模糊综合评估[J].电力系统保护与控制,2013,41(7):136-141.
