电动汽车换电站定址分容研究

高赐威，段天琪

（江苏省智能电网技术与装备重点实验室（东南大学），南京 210096）

换电模式是电动汽车发展重要的商业技术模式之一，其优点在于：①采用电池租赁方式可降低用户的购车费用；②对电池进行集中充电可采取慢充方式，避免因充电不当造成的电池寿命缩短；③对电池进行集中管理可减少电动汽车随机充电给电网带来的波动；④集中型充电站可对替换下的电池进行梯次利用，进而提高电池的利用率、减少电池对环境的二次污染。

文献[1]使用了粒子群优化算法，建立分区分地块的优化规划方法，并在优化规划过程中引入分散系数的概念，以换电需求、电池续航里程为约束，建立了换电站和配送站优化规划模型。文献[2]对集中充电及配送模式和换电站模式等2种充电站建设模式进行综合经济效益分析，提出2种充电站建设模式的适用范围及换电站规划建设思路。文献[3]结合电动汽车发展规划构建了充换电设施建设规划设计模型与算法，研究充换电设施布点规划、城际互联网络等难点并提出解决方案。文献[4]将充电模式和换电模式进行有效的结合，对不同类型的车辆采用与其行驶特点相适应的供能方式，由此提出综合了集中换电站、配送站和快速充电站的供能设施规划原则，并引入LCC理论建立相应的最优规划模型。文献[5]建立了换电模式下电动汽车电池充电负荷及优化模型，对2种电动汽车换电模式即充换电模式和集中充电统一配送模式的结构、运营流程进行了分析。文献[6]对电动汽车换电站的选址规划布局进行研究，并开发基于地理信息系统的用户可操作的充换电站网络规划系统，在选址分析的基础上进行了充换电站网络规划方案的基础建模和规划系统功能算法的设计：建立了换电站日服务能力需求测算和单站日服务能力需求测算模型，并且进行了服务能力、服务半径、电网负荷峰谷差率以及二氧化碳减排等方面的算法分析，从而实现换电站的选址规划布局。文献[7]对北京地区“十二五”期间电动汽车保有量及配套服务设施建设需求进行了预测，并给出了充换电营销服务体系的布点原则及布局方案，同时评估了充换电营销服务体系对电网的影响。文献[8]针对充换电网络的规划与运行进行了详细分析，从电池数量、充电站的选址定容2个方面对换电网络的规划问题进行了研究，并分析了换电网络在实际运行阶段该如何进行电池调配以及充电管理。文献[9]针对“集中充电、统一配送”模式下的电池数量规划问题展开研究，根据原始可用信息和规划目标要求的不同，分为远期与近期2个规划阶段，并对该问题进行建模，形成涵盖多阶段的电池数量综合规划模型。文献[10]介绍了美国等发达国家电动汽车能源供给设施建设的现状并进行了对比分析，阐述了国内电动汽车能源供给设施建设的现状，分析了国内交流充电桩、充电站及电池更换站等主要能源供给设施的类型及特点。

本文针对电池换电站的规划问题，综合考虑电动汽车用户的行驶时间和排队等待时间，将定址分容问题进行解耦，建立了换电站的定址分容模型。

1 电动汽车换电站运营模式

本文中电动汽车换电站只考虑其更换电池的功能，暂不考虑其充电功能。当前电池充电存在2种模式，集中充电模式与换电站充电模式。前者由集中型充电站提供充电服务，并将电池配送至不具备充电能力的配送站（换电站）提供换电服务；后者换电站同时具备充电和换电功能。本文中仅就电动汽车换电站的换电功能进行研究，关于充电能力的配置已有较多文献研究[11—12]，本文主要研究充换电网络中换电站的规划。

电动汽车换电站的功能定位及建设要求与以往的充电站或变电站有很大区别，所以现有关于充电站或变电站的研究无法直接应用于换电站的定址分容规划，但相关思路可供借鉴。

2 电动汽车换电站定址分容模型

对电动汽车换电站进行定址分容研究，其目的是更好地满足电动汽车用户更换电池的需求，使用户的行驶时间和排队等待时间都在可接受的限值内，在此前提下最小化换电站的建设成本。模型将定址分容问题进行解耦，先选择换电站的站址，在此基础上计算换电站的容量配置，最终得到换电站的定址分容模型。

2.1 电动汽车换电站定址分容模型说明

电动汽车换电站在规划建设时需考虑的因素有占地面积、地价、换电设备套数等。本文中换电站定址分容模型为

式中：F表示电动汽车换电站的总建设费用，NC表示待建设的换电站个数，δCi表示第i个换电站是否建设的二元决策变量，取值为1表示该待选站址将建设换电站，取0表示不在该待选站址建设换电站；αCi表示第i个换电站的年均费用系数，假设各站的年均费用系数相同，设为αC0；Pi表示第i个换电站的容量；CFCi(Pi)表示第i个换电站固定成本，其为容量Pi的函数；CMCi（Pi）表示第i个换电站的维护检修费用，其为容量Pi的函数；αS表示购买土地的年均费用系数；Si表示第i个换电站的面积；Plandi表示第i个站址的地价，万元/m2。

电动汽车换电站的容量与换电设备套数密切相关，所以可以使用换电设备套数来替代目标模型中的换电站容量。

当①各站选择的换电设备类型相同；②把换电站的占地面积平均到每套换电设备，此时目标模型可变为

式中：NEi表示第i个换电站配置的换电设备套数；CF0表示一套设备的固定投资费用。

该模型求解过程中需要满足2个约束条件：电动汽车平均行驶时间限制和电动汽车换电站内排队时间限制，约束条件对换电站的定址和分容方案进行了限制，模型的求解过程即为求解出满足约束条件的换电站最优的建设方案。

本文建立的换电站定址分容模型中待求解变量有换电站待选站址是否建设的二元决策变量δCi、换电站配置的换电设备套数NEi；已知量有每时刻的换电需求量P、交通网络相关参数、各待选站址情况。通过将已知量、控制变量代入模型，可得到待求解变量值。当控制变量发生改变时，通过求解模型可以得到不同控制变量下的待求变量值。

2.2 换电站定址分容方案确定流程

在本文中，建立电动汽车换电站定址分容模型，需要以下3个已知量：

·城市或区域内的换电需求情况：该换电需求情况可表征为需要换电的车辆数目随时间变化的关系。

·电动汽车所在位置的概率分布：本文中设定电动汽车的位置服从某种概率分布，根据该分布可以得知地图中电动汽车的位置。已知量①表征了各个时刻需要换电的电动汽车数量，根据电动汽车的分布概率，可知每个时刻地图上各点需要换电的车辆数目。

·交通网络参数：包含交通网络中道路长度和电动汽车的行驶速度，从而能够计算电动汽车在交通网络中的行驶时间。

获知以上已知量后，确定电动汽车换电站方案的流程具体如下图1所示。

图1 方案确定流程图

（1）依次对换电站进行选址

站址选择的原则是在已知的待选站址中选择换电站，在满足电动汽车平均行驶时间的条件下最小化换电站的数量。

·首先取换电站数量为1，使用已知量计算电动汽车到换电站的行驶时间，多次抽样电动汽车的位置，对所有电动汽车的行驶时间取平均值。

·换电站数量为1，针对换电站的选址的多种情况进行计算，选择平均行驶时间最短的选址方案，作为第1个换电站的站址。

·增加换电站的数量至2，同样的，第2个换电站的站址会有多种情况，选择平均行驶时间最短的选址方案。

·继续增加换电站的数量，直到电动汽车的平均行驶时间达到要求，选取换电站数量最少的方案作为选址方案。

（2）对换电站进行容量配置

·对于选址方案中的换电站站址，所有换电站的换电设备容量从1开始增加，每个换电站的容量同时增加。

·多次抽样电动汽车的位置，计算电动汽车平均排队时间，当平均时间符合要求时，停止增加容量，此时所有换电站的换电设备容量数均相同，将此方案作为初始方案。

·在初始方案的基础上，选择1个换电站，对其减少1套换电设备，此时计算平均排队时间，此时会有多种选择方案，对于平均时间依然在限制值内的方案，计算其建设成本，选取建设成本最低的方案。

·继续对换电站减少1套换电设备，同样的，选择平均排队时间符合要求、建设成本最低的方案。

·如若再减少1套换电设备，平均排队时间无法再满足要求，该方案作为电动汽车换电站定址分容最终方案。

2.3 电动汽车行驶时间计算

电动汽车行驶到换电站的时间，是确定换电站站址方案的关键因素。本模型中设定电动汽车选择最短路径到达换电站，使用Dijkstra（迪科斯彻）最短路径算法计算该路径。

下面对Dijkstra最短路径算法进行简要的介绍：交通地图可以表示为一个带权图，用图的顶点表示道路交叉口，用图的各条边表示城市里的道路，各边的权值表示该路线的长度。

Dijkstra算法中，首先求出长度最短的一条路径，然后参照它求出长度次短的一条路径，依次类推，直到从起点到其他各终点的最短路径全部求出为止。假定电动汽车在道路上以匀速行驶，则求得最短路径等同于求得最短行驶时间。

设集合S存放已经求出的最短路径的终点。初始状态时，集合S中只有一个源点，不妨设为v0。以后每求得一条最短路径（v0,…,v1），就将vk加入到集合S中，直到全部顶点都加入到集合S中，算法结束。

为了当前找到的从源点v0到其他顶点的最短路径长度，再引入一个辅助数组dist[]。他的每一个分量dist[i]表示当前找到的从源点v0到终点vi的最短路径的长度。它的初始状态是：若从源点v0到顶点vi有边，则dist[i]为该边的权值；若从源点v0到顶点vi没有边，则dist[i]为+∞。

设第一条最短路径为（v0，vk），其中k满足：disk[k]V是图中顶点的集合} 。假设下次最短路径的终点是vj，则它或者是（v0，v）j，或者是（v0，vk，v）j。其长度或者是从v0到vj的权值，或者是dist[k]与从vk到vj的权值之和。一般情况下，下一条最短路径总是在“由已产生的最短路径再扩充一条边”形成的最短路径中得到。假设S是已求得的最短路径的终点的集合，则可证明：下一条最短路径必然是从v0出发，中间经过S中的顶点再扩充一条边便可到达顶点vi(vi∈V-S)的各条路径中的最短者。若设下一条最短路径（v0,…,vk）的终点是vk，则有

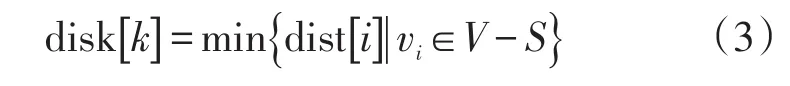
在每次求得一条最短路径之后，其终点vk加入集合S，然后对所有的vi∈V-S，修改其dist[i]，函数为dist[i]=min{d ist[i],dist[k]+G.getWeight(k,i)} ，其中，G.getWeight(k,i)是边（vk，v）i上的权值。

图2中5个点组成地图，5个点之间的距离如图2所示，根据地图编写邻接矩阵，两点间没有连线，则矩阵中用无穷大表示。

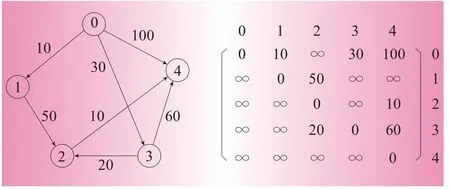
图2 Dijkstra算法举例图示

对于图2中的交通网络图，使用Dijkstra最短路径算法，能够求得从原点v0出发，依次到达各点的最短路径，分别是10、50、30、60，其过程见表1。

表1 Dijkstra算法过程

2.4 换电站内排队等待时间计算

电动汽车在换电站内排队等待时间，是确定换电站容量建设的关键因素。

电动汽车到达换电站后，可能不能马上更换电池，而是需要排队等待。对于某一辆电动汽车，在时间t1时到达换电站，假设该换电站内有n套更换电池设备，设备更换一次电池需要用时t2。若①n套更换电池设备尚有空余，则该电动汽车无需排队，等待时间为0；②n套更换电池设备都在使用，n套设备完成换电的时间分别为tx1、tx2至txn，而且t1时已有m辆电动汽车在排队等待，对于该辆电动汽车，其排队时间与上述量密切相关，为

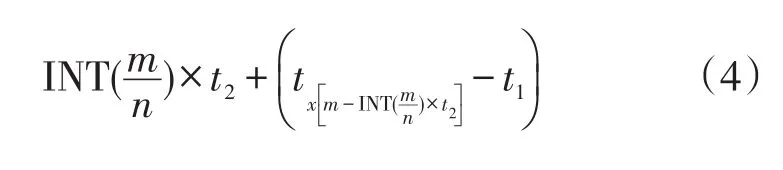
式中：INT（t）表示对t取整。

3 实例分析

3.1 算例分析

3.1.1 待选电动汽车换电站

为了验证所提出的模型，本文基于以下几个假设对某城市的电动汽车换电站选址问题进行实例分析。

（1）本算例对该城市24 h内电动汽车更换电池情况进行仿真，该城市更换电池的数量总需求如图3所示，表示24 h中需要换电的电动汽车数量变化情况，是算例中的已知量。使用平均分布模拟该城市中电动汽车的位置分布。

图3 城市24 h更换电池需求

（2）该城市电动汽车换电站待选站址有15个，每个换电站的换电设施最大建设容量为5套，单套换电设施的占地面积为20 m2。

（3）每套换电设施能为1辆电动汽车更换电池，换电设施为一辆电动汽车换电池需要用时5 min。

3.1.2 城市交通网络

图4为某城市的主要交通网络图，购买土地的年均费用系数αS为0.1。待选站址在交通网络图中的情况如表2所示，假设电动汽车在每条道路中以30 km/h的速度匀速行驶。

图4 城市交通网络图

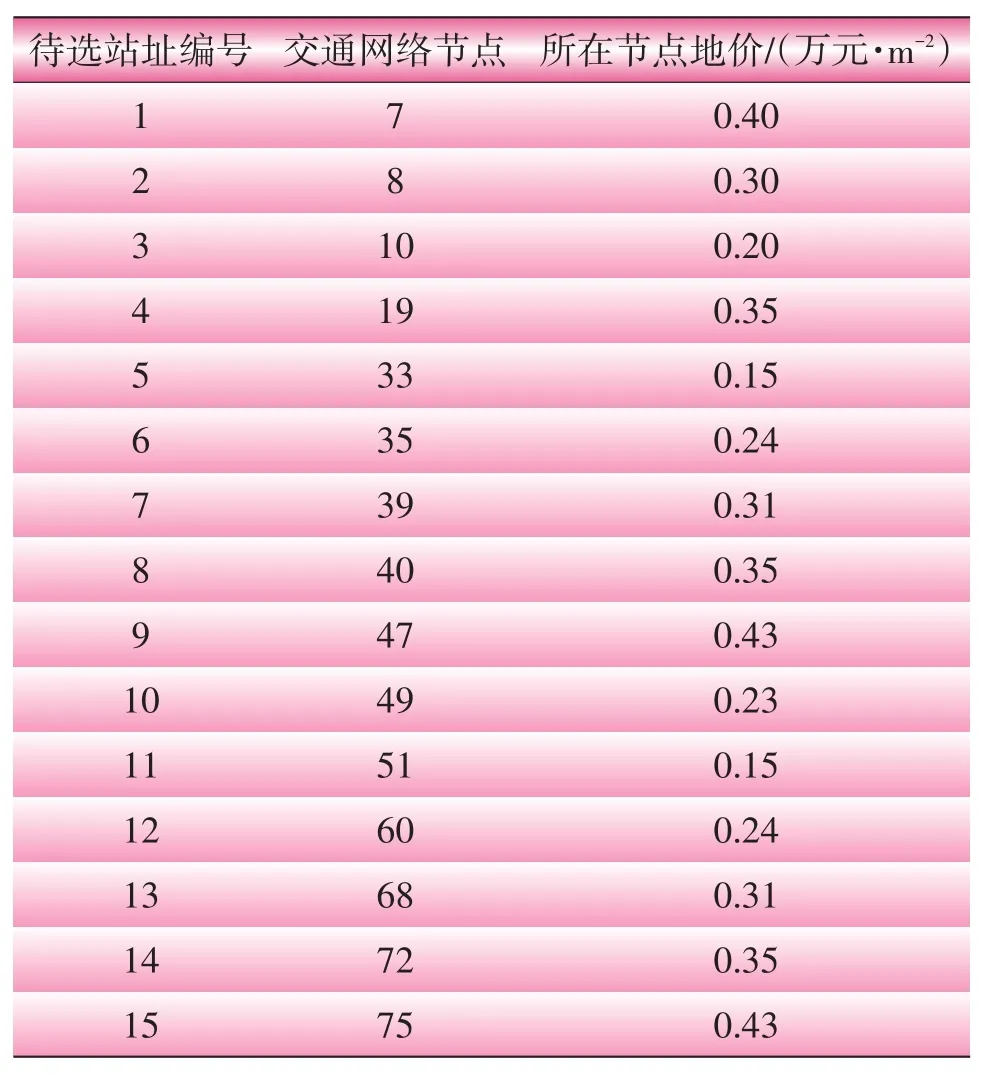
表2 待选站址在交通网络图中的情况

3.2 电动汽车换电站定址分容模型求解

3.2.1 选址方案求解

上图3是某城市24 h的更换电池需求曲线，本算例中以5 min为时间尺度，每5 min进行一次计算。对于每个时间点上的需更换电池车辆数，使用平均分布散布到图4的交通网络图中，然后通过Dijkstra最短路径算法计算出车辆到换电站的最短路径。

使用平均分布模拟电动汽车的位置，每次取样电动汽车分布的位置都会不一样。如果取样次数充分多，该计算方法能从概率的角度揭示电动汽车的位置分布，可以对换电站的选址方法进行充分的验证，保证电动汽车能够在在限制的时间范围内驶达换电站。

对于换电站定址模型的求解，采用依次逐渐增加待选站址数量的方法。本算例中共有15座换电站待选站址，其计算的过程是：

（1）首先计算只有1座换电站的方案，对24 h内的时间点进行计算，使用平均分布对电动汽车的位置信息进行100次抽样。

（2）计算电动汽车到换电站的平均行驶时间，选择使平均行驶时间最短相应的换电站。

（3）增加1座换电站，对24 h内的时间点进行计算，使用平均分布对电动汽车的位置信息进行100次抽样。

（4）计算电动汽车到换电站的平均行驶时间，选择平均行驶时间最短的换电站方案。

（5）继续增加换电站的数量，直到平均行驶时间达到要求，选取该方案作为换电站选址方案。

上述计算过程共选出了4套换电站选址方案，其站址编号如表3所示。

表3 换电站站址选址方案

在选出的4套换电站选址方案中，所有方案的站址编号只有最后一位不一样，这是由于换电站的选址是带方向的搜索过程，优先选出能使平均行驶时间短的换电站站址，因此4套方案最后一位之前的站址选择都一样。在选择第9个站址时，共有4个站址能使平均行驶时间满足限值，因此选择其作为最后选择的站址，选址方案的站址数量确定为9个，共选出4套选址方案，如图5所示。

图5 选址模型求解计算结果

在求解换电站选址方案的计算过程中，逐步增加换电站的数量，电动汽车行驶到换电站的平均时间随之逐步下降，直到满足时间约束。图6反映了在24 h全天模拟中，对于方案1，电动汽车行驶到换电站的平均时间随换电站数量的变化关系。

3.2.2 分容方案求解

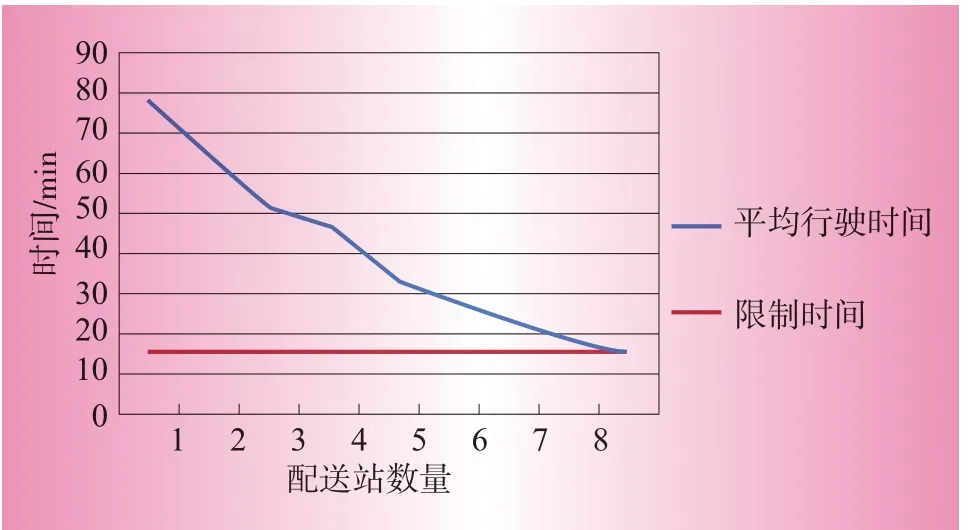
图6 平均行驶时间与换电站数量关系

在文3.2.1已求解出换电站选址方案的基础上，对分容模型进行求解。

对于一套换电站的选址方案，下面计算其需要配置的换电设备数量。使用与文3.2.1中类似的算法，换电设备的数量从最低值开始，即每座换电站的换电设备数量均为1套，计算24 h内电动汽车在换电站内的排队等待时间，对电动汽车的分布进行100次抽样，计算平均排队时间，如果排队时间超过约束限制，则将每座换电站的换电设备数量增加到2套，再次计算平均排队时间，直至排队时间满足约束限制，这样得到初始方案，初始方案中每座换电站内的换电设备套数都相同，均为5套。

在求解初始方案时，逐步增加换电站内换电设备的数量，电动汽车排队等待时间随之逐步下降，图7表征了这一关系。

图7 平均排队时间与换电设备数量关系

再对该初始方案进行修正，尝试将初始方案中任一座换电站的换电设备减少1套，计算平均排队时间是否满足要求，若满足要求再计算本次减少换电设备使总建设成本降低的金额，对初始方案中的每一座换电站都进行该计算，选择能使总建设成本降低数额最多的换电站，将该换电站的换电设备减少1套，如此形成新的方案。再对该新方案进行上述同样的计算，继续选择减少1套换电设备后，依然满足排队等待时间的、能使总建设成本降低最多的换电站，将该换电站的换电设备减少1套。如此继续进行本计算，直到任一换电站减少换电设备后都无法满足排队时间约束，计算停止，本方案为算例计算结果。

对于文3.2.1已求解出的4套换电站选址方案，按上述计算过程求解出对应的容量配置和建设总成本，如表4所示。

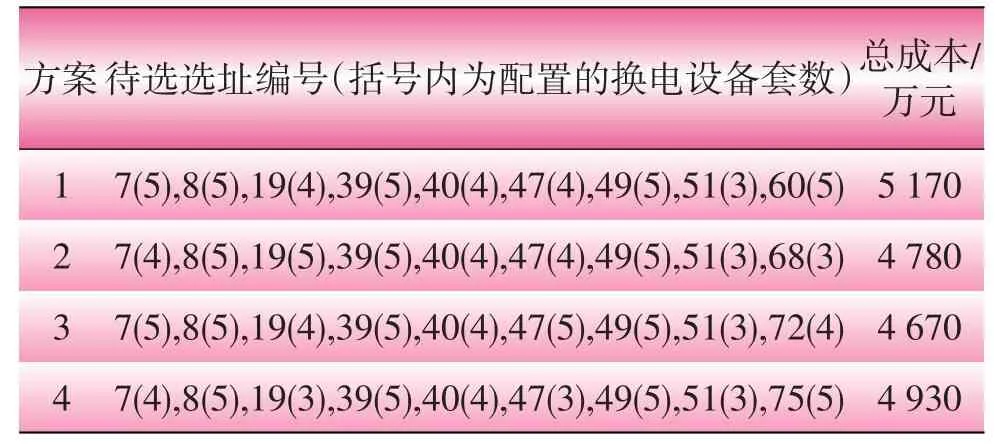
表4 换电站容量配置方案

在初始方案的基础上求解最终方案，是进行带方向的搜索，搜索目标是在可进行减少换电设备的换电站集合中，选择使总建设成本下降最多的换电站，因此在该项计算中，随着每次找到搜索目标，逐渐减少换电设备套数，总建设成本下降地越来越慢，而排队等待时间逐渐增长，直到逼近约束值。

以方案1为例，对于其从初始方案形成最终方案，总共进行了5轮减少换电设备的搜索，这5轮搜索并减少换电设备，对总建设成本和平均排队等待时间的效果如图8所示。

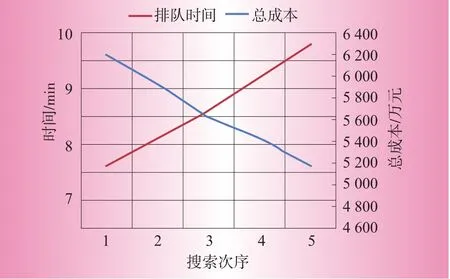
图8 总建设成本和平均排队时间变化曲线

同时，对上述搜索过程进行分析，其实质是通过电动汽车排队时间约束，筛选出能够被减少换电设备的换电站，由于每套换电设备占地面积相同，于是每座换电站内换电设备的建设成本与该站址的低价成正比，所以搜索的结果即为在已筛选出的换电站集合中，对所在地价最高的换电站减少一套换电设备。

对于4套电动汽车换电站定址分容方案，电动汽车的平均等待时间与总建设成本如表5所示。

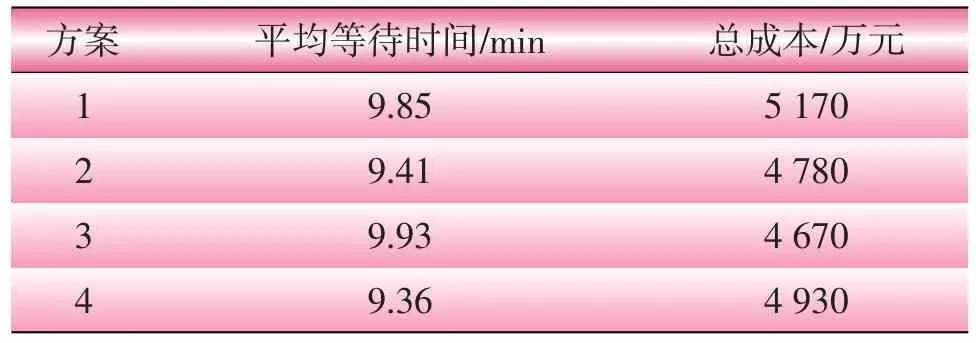
表5 等待时间与总建设成本

分析表5的数据，方案1的总成本最高，但对电动汽车服务能力却并不是最好的，平均等待时间要比方案2和方案4长。其原因是不同的方案其选址不同，不同的选址方案造成了建设资金使用的有效性。

综合表3（换电站选址方案）与表5的数据，可得到4种方案的平均行驶时间、平均等待时间和建设成本。综合4种方案的3项数据水平，本算例应选择方案2作为换电站定址分容方案。

3.3 电动汽车换电站定址分容模型灵敏度分析

3.3.1 换电需求改变对定址分容的影响

对图2的更换电池需求进行改变，场景1是在图2整体需求水平基础上上升50%，场景2为原图2中的换电需求，场景3为在图2整体需求水平基础上下降50%。3个场景的电池需求情况如图9所示。

图9 不同场景下更换电池需求曲线

针对以上3个场景中不同的更换电池需求，对其进行相应的换电站定址分容计算，比较3个场景对应的选址分容方案及其总建设成本，比较结果如表6所示。

表6 不同场景下选址分容方案及总成本

分析表6可知，随着电动汽车换电需求的变化，换电站的选址分容方案及总成本也随之变化。从换电站建设的角度理解，不同的换电站建设方案，其能够应对的电动汽车换电需求是不同的。

当换电需求在算例的基础上提高50%时，换电站建设总成本需要提高58.5%；而换电需求在算例的基础上降低50%后，换电站建设成本能够减少23.6%。

3.3.2 行驶时间限制改变对定址分容的影响

电动汽车行驶到换电站的行驶时间限制是选择换电站选址方案的关键因素，而不同的选址方案也将对换电站的容量配置产生重要影响。

本文实例分析中设置的行驶时间限制为15 min，现将行驶时间限制分别设置为9 min、11 min、13 min、15 min、17 min、19 min、21 min，分别计算对其计算选址分容方案，并计算其总建设成本。结果如表7所示。

表7 不同行驶时间约束下的换电站建设方案

分析表7可知，对应不同的行驶时间约束，换电站的建设方案及总成本也相应的变化。从换电站建设的角度理解，不同的换电站建设方案与成本所能提供的换电服务相应也不同，其趋势是：换电服务能力要求越高，其建设成本也逐渐提高。对于换电站定址分容方案的确定，应结合其服务能力的要求和成本进行综合考虑。

4 结论与展望

本文提出了一种电动汽车换电站的规划模型，在电动汽车用户行驶时间和排队时间的约束下，能够求解出最具经济性的建站方案，并在算例中使用该模型得到了结果。灵敏度分析计算表明换电需求和行驶时间约束均为影响换电站方案确定的关键因素。

本文仅以用户行驶时间和排队时间作为建站约束，后续研究中可加入电池数目、道路拥堵情况等约束，同时换电站的充电功能也可加入模型中。以上均有待进一步研究。

[1]权会霞.城市电动汽车充换电设施优化布局研究[D].北京：华北电力大学，2013.

[2]张伟华.电动汽车充换电服务网络构成研究[D].北京：华北电力大学，2012.

[3]刘群峰.电动汽车充换电服务网络规划研究[D].北京：华北电力大学，2013.

[4]肖贤，周步祥，付锦，等.电动汽车低渗透率下的供能模式及供能设施的LCC最优规划[J].电力系统保护与控制，2013，41（20）：53-61.

[5]罗卓伟，胡泽春，宋永华，等.换电模式下电动汽车电池充电负荷建模与有序充电研究[J].中国电机工程学报，2012，32（31）：1-10.

[6]周利梅.电动汽车换电站选址规划布局研究[D].济南：山东大学，2012.

[7]邱吉多.北京市电动汽车充换电营销服务体系研究[D].北京：华北电力大学，2012.

[8]高赐威，吴茜.电动汽车换电模式研究综述[J].电网技术，2013，37（4）：891-898.

[9]高赐威，吴茜，薛飞，等.换电模式下电动汽车电池组需求规划[J].电网技术，2013，37（7）：1 783-1 791.

[10]张文亮，武斌，李武峰，等.我国纯电动汽车的发展方向及能源供给模式的探讨[J].电网技术，2009，33（4）：1-5.

[11]高赐威，张亮.电动汽车充电对电网影响的综述[J].电网技术，2011，35（2）：127-131.

[12]高赐威，张亮，薛飞，等.考虑集中型充电站定址分容的电网规划研究[J].中国电机工程学报，2012，32（7）：40-46.