基于改进灰色马尔科夫预测法的中长期负荷预测

夏耀杰，程浩忠

（1.上海电力学院 电气工程学院，上海 200093；2.上海交通大学 电子信息与电气工程学院，上海 200240）

1 背景

中长期负荷预测是制定电力系统发展计划的基础，也是规划工作的重要组成部分，其目的是为合理安排电源和电网的建设进度提供宏观决策的依据，使电力建设满足国民经济增长和人民生活水平提高的需要。

影响系统负荷的因素大部分具有规律性，从而为实现有效地预测奠定了基础。目前用于负荷预测的方法很多，如：回归分析法、外推预测法、相似日法、神经网络模型等等，这些方法各有优劣。其中灰色系统理论用于负荷预测，特点是不需要大样本量作为基础，也因此被广泛用于各种预测[1]。但灰色理论模型实质上是指数模型，累加生成不能减弱序列的随机性，从而不能提高预测精度[2]。因此对灰色系统理论的改进也有很多，文献[3]—文献[5]是对灰色预测模型的内部流程改进，包括对初值选取和累加序列改进，不过是模型本身还是指数模型，无法适应波动较大情况。文献[6]，文献[7]是残差修正的灰色预测模型，证明了残差修正能有效提高灰色模型的拟合精度，然而无法满足预测精度较高的要求。文献[8]使用马尔科夫链对灰色模型修正，证明使用马尔科夫链可以有效提高灰色预测的精度，不足是马尔科夫模型在数据样本量受到局限时会出现由于状态转移概率矩阵的不稳定而影响预测精度的情况。文献[9]使用基于改进的马尔科夫对航空备件需求进行预测，通过改进马尔科夫的状态转移矩阵提高其预测精度，但是该模型对于长期预测任务无法胜任。文献[10]用灰色马尔科夫预测负荷，根据灰色模型的残差通过马尔科夫链进行修正，但是此模型应用于波动性较大序列时会出现偏离预测值较大的不利情况，在这种情况下即使使用马尔科夫修正也只是小范围修正，无法在很大程度上提升预测精度。

为得到更好的拟合度并且提高预测精度，本文提出一种基于残差修正的GM（1，1）模型和改进的马尔科夫链修正模型相结合的方法，首先使用灰色模型对中长期负荷进行预测，然后用残差模型提高灰色模型拟合度，最后使用改进的马尔科夫链对预测偏离加以修正，借以提高负荷预测精度。算例样本数据采用某市1998年到2013年最大负荷验证了算法的有效性。

2 改进的灰色马尔科夫理论介绍

2.1 GM（1，1）模型

建模步骤：

（1）采集原始数据序列

式中：X(0)为原始数据序列；n为采集的样本数。

（2）对原始序列做一次累加序列（1-AGO）数据生成

（3）建立白微分方程

此方程为灰色微分方程x(0)(k)+az(1)(k)=b的白化方程，亦称影子方程。其中a为发展系数，(a,b)=(BTB)BTY，a和b是待定参数。

（4）利用最小二乘法求解参数a和b

GM（1，1）模型x(0)(k)+az(0)(k)=b的时间响应序列xΔ(1)(i+1)，计算公式如下

其中，i=1,2,…，n。

对一次累加生成数列的预测值进行一次累减生成（1-AGO），得到原始数据的还原预测值。

还原值

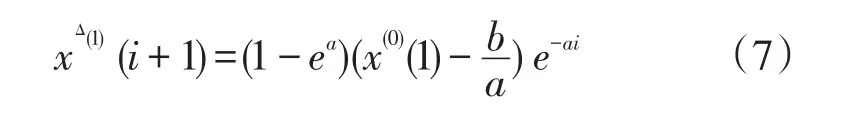
其中，i=1,2,…，n。

求出原始数据的还原预测值与真实值之间的残差值和相对误差，即进行残差检验。如果通过残差检验，则可以用所建的模型进行预测，否则要进行残差修正。

2.2 残差检验

残差大小检验，即对模型值和实际值的残差进行逐点检验。首先按模型计算xΔ(1)(i+1)，将xΔ(1)(i+1)累减生成xΔ(0)(i)，最后计算原始序列x(0)(i)与xΔ(0)(i)的绝对残差序列

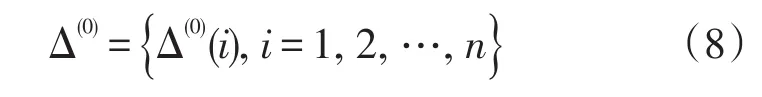
相对残差序列并计算平均相对残差

给定α，当＜α，且Φi＜α成立时，称模型为残差合格模型，一般α取0.01～0.05。如果模型的相对误差平均值在1%及以下，说明模型的精度等级为一级；如果大于1%且小于5%，模型的精度等级为二级；如果大于5%且小于10%，则为三级；当其大于10%且小于等于20%，则模型的精度等级为四级。

2.3 GM（1，1）残差模型

当原始数据序列x(0)建立的GM（1，1）模型残差检验不合格或精度未达到要求时，可以用GM（1，1）残差模型来修正以提高精度。

若原始数据序列x(0)建立的GM（1，1）模型如式（6），可获得生成序列x(1)的预测值，定义残差序列

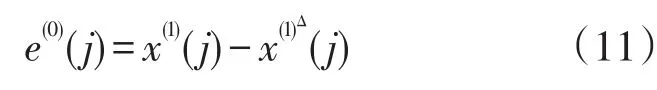
若取j=1,2,…，n则对应的残差序列为

计算其生成序列e(1)，并据此建立相应的GM（1，1）模型

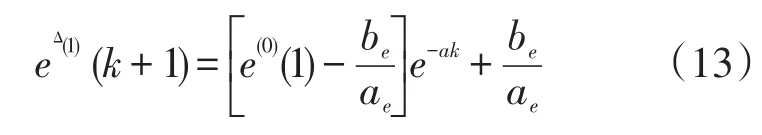
得修正模型

通过式（15）得还原值

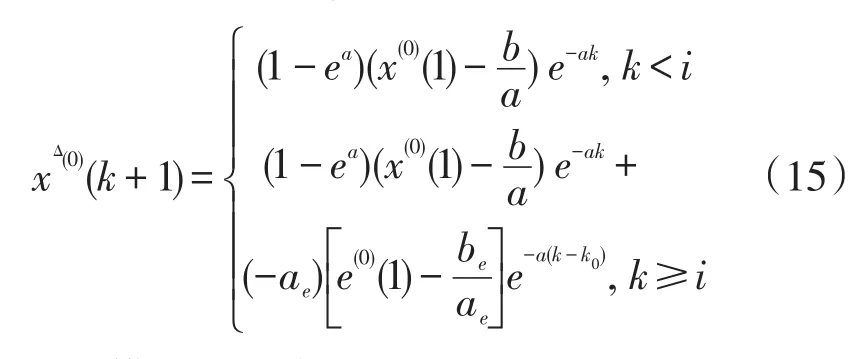
应用此模型时要考虑：

（1）一般不是使用全部残差数据来建立模型，而只是利用了部分残差，例如：式（14）和式（15）中的i为修正起始点，起始点之前不进行修正。

（2）修正模型所代表的是差分微分方程，其修正作用与δ(k-i)的i取值有关。

这一节是本文较文献[11]改进的地方，本文对灰色模型进行残差修正使得在误差修正前提高预测序列与实际数据贴合度。

2.4 马尔科夫链误差修正模型

为建立马尔科夫预测模型，首先给出以下定义。

·状态。是指事物在某个时刻出现的一种结果，随着事件及其预测的目标不同，状态可以有不同的划分形式。这里定义负荷在某一个时刻的相对误差精度范围Ei为n种状态(E1,E2,…,En)中一种。

·状态概率向量。在某阶段所有状态可能出现的概率的向量，用S表示，即状态概率向量SS=（S1,S2,…,Sn），满足以下条件

其中，i=1,2,…，n；Si为状态概率，表示在某阶段系统处于状态Ei的可能性的大小。

·状态转移概率。在事件的变化过程中，从某一种状态出发，经过k转移到其他状态的可能性，称为k步状态转移概率。用Pij(k)表示k步转移概率，即

其中，i,j=1,2,…,n。

·状态转移概率矩阵。假定某一被预测的事件有（E1,E2,…,En）共n个可能的状态，记Pij(k)为从状态Ei转为状态Ej的k步状态转移概率，则作n×n阶矩阵。

具体预测数值偏移修正模型建模步骤如下：

（1）划分负荷预测相对误差的阶段和状态

对于负荷预测来说，一般以时间t为参数表示阶段，负荷在某一阶段的相对误差情况作为状态量，一共分为n种状态，步骤如下：①找出用于相对误差数据中的最大值Xmax和最小值Xmin，确定取值空间为[Xmin,Xmax]；②确定相对误差的状态数量n，求出状态步长L=(Xmax-Xmin)/n；③将第t阶段的相对误差量xt转化为该阶段的状态情况Yt= |(xt-Xmin)/L|；

（2）确定状态转移概率和状态转移概率矩阵

通常，状态转移概率的理论值是未知的，为了求出Pij，一般采用频率近似概率的思想来计算。当样本足够大时，可以在样本空间内，近似地用状态相互转移的频率来统计状态量和状态转移。

设Mi为处于状态Ei的样本数，Mij(k)为状态Ei经过k步转移到状态Ei的样本数，用Pij(k)表示k步转移概率，如式（18）

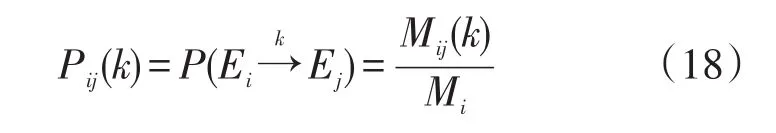
其中，i,j=1,2,…,n；则相应的k步状态转移概率矩阵P(k)就可以表示如式（19）所示

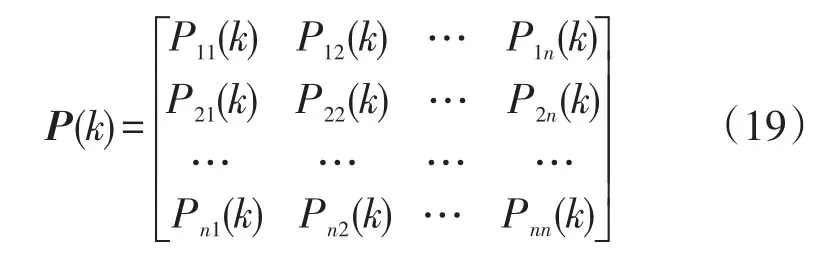
（3）建立马尔科夫修正模型

只要知道t-k阶段的状态和状态转移概率矩阵，在理论上就可以预测出t-k阶段以后任意阶段的状态向量，计算公式如式（20）

式中：P(k)为k步状态转移概率矩阵，若已知初始状态概率向量SS(0)和转移概率矩阵P(1)，则可以求出系统在任意阶段的状态概率向量。

（4）对马尔科夫预测模型进行改进

由于灰色模型特点是不需要大量样本，在文献[11]中直接使用马尔科夫链进行修正并未考虑原始数据不足引起的缺陷。因为当样本有限时马尔科夫模型在实际算例中由状态出现的频率计算出的状态转移概率矩阵会有一定的不稳定性，故为了配合灰色模型的特点，进而减少由一步状态转移所产生的误差，本文采用连续3步平均法进行预测，计算公式如式（21）

其中：P(1)、P(2)、P(3)由式（18）和式（19）得。

改进的灰色马尔科夫模型建模的步骤如图1所示。

3 建模及算例分析

3.1 建立GM（1，1）模型并残差修正

图1 改进灰色马尔科夫模型建模的步骤

原始样本选取某市1998年至2013年最高负荷，数据来源于电网公司统调数据。其中1998年至2010做训练样本，2011年至2013年做预测误差分析样本，由于1998年至2004年间样本增长率较稳定且没有畸变较大的点，故样本分析仅选取2004年至2013年，2004年至2013年样本结构如图2所示。

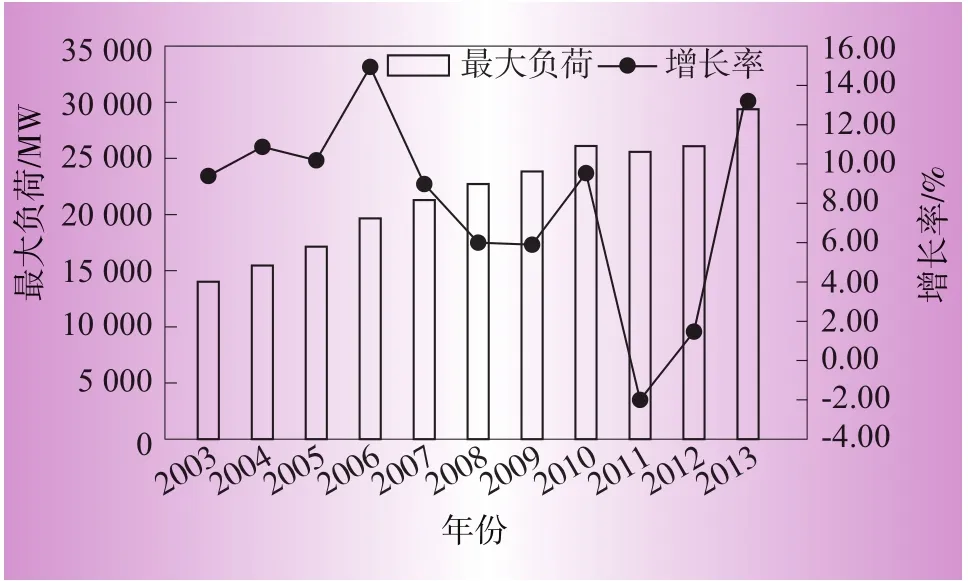
图2 最大负荷及增长率

由图2可见，2010之前每年增长维持在正增长范围约为5%到20%之间，2011年出现负增长约为-2%，2012年增长小于5%，2013年增长回到15%，可以明显看出2011年至2013年增长曲线严重偏离了2004年至2010年之前的增长率曲线，在这种情况下认为是畸变较大部分。

灰色模型和残差修正的灰色模型的建模结果如图3所示，按照残差修正原理，在2006之前不需要进行残差修正，故2006年之前2条曲线重合，从2006年开始，残差修正后的灰色模型总体上更好地拟合了负荷的真实变化曲线。随着原始值的波动，例如：2006年至2008年原始曲线呈凸型，此时未残差修正的模型偏离较大，残差修正则一定程度上修正了偏移，提高拟合度。

图3 灰色预测结果和残差修正后的结果

2011年至2013年样本值出现与1998年至2010年有较大波动，残差修正后虽然使得误差偏离变小，但还是处于较大误差范围内，如表1所示，相对误差一度到达24%。下面使用改进马尔科夫链进行修正，文献[11]使用残差数据进行状态划分，而本文使用残差修正后灰色模型的预测误差进行状态划分以提高对误差的修正。

表1 灰色模型预测值及残差修正相对误差

3.2 改进的马尔科夫误差修正

表2 状态划分

表2按照2.4节内容进行状态表的编制，相对误差值由2002年至2010年预测的值与原始值得出，共有4个状态分别表示，相对误差范围-0.03～-0.015为较大低估，为状态1；-0.015～0为较小低估，为状态2；0～0.015为较小高估，为状态3；0.015～0.03为较大高估，为状态4。

相应结果如表3所示。

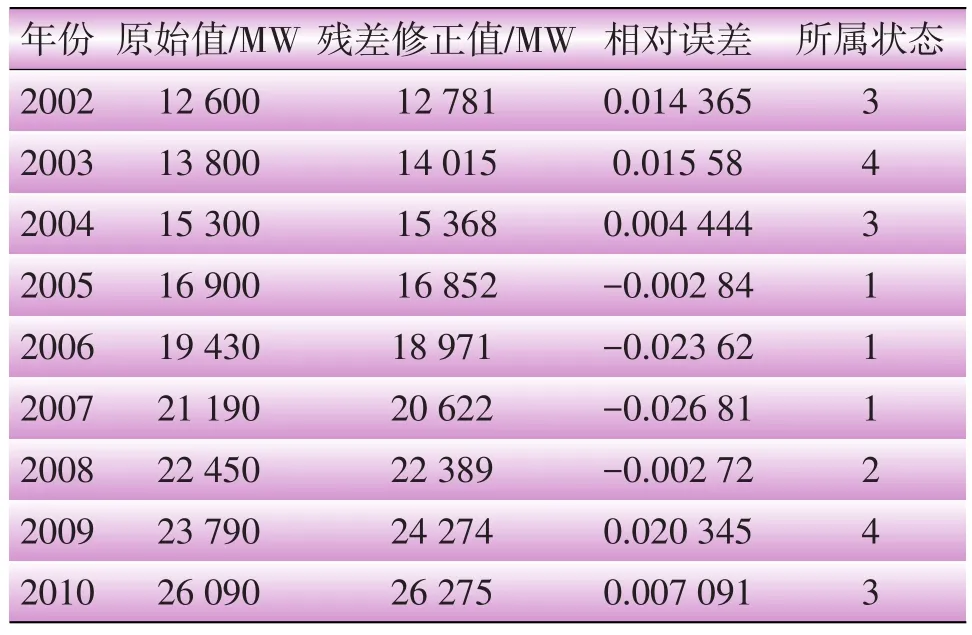
表3 残差修正值和相对误差及所属状态

由表3可以得到残差修正值相对误差的状态转移具体频数统计，总频数为9。

为求出2011年的预测值，根据表3中的状态情况，结合式（21）可得2011年状态概率向量，同理可得2012年及2013年的，具体数值如下表4所示。

表4 改进马尔科夫预测状态向量

由表4可以看出，2011、2012、2013年状态向量值均处在状态4，即较大高估的概率比较大，误差范围是0.015～0.03。因此可以对2011至2013的预测数据做进一步修正。具体结果见表5。

表5 改进马尔科夫链修正值及修正残差相对误差

由表5可以看出改进的马尔科夫修正对2011、2012、2013年预测结果是有明显修正，除了2012年以外，修正后的结果相对误差均在4%以内，可见由实际预测误差进行修正能在一定范围有限提高预测精度。2012年这个点可以从图1中明显看出，由于其畸变性较大，对于预测模型是很大挑战，即使用改进的马尔科夫链修正，相对误差还是达到了8%。

4 结论

负荷受多种因素影响，波动性较大，也比较容易出现畸变，特别如本文所使用的样本，其中2011至2013年的负荷值与1998至2010年的走势出现很大分歧，增长率一度变成负值和相当小的值以及突然增大，如此波动使得一般模型难以精确预测负荷序列，为预测带来了很大难度。算例结果显示，直接使用灰色模型预测相对误差最大达到20%，故用残差修正灰色模型以提高拟合精度，而后再用改进的马尔科夫链修正偏差，使得3年的预测值相对误差有2年保持在5%以内，说明本文提出的方法对畸变较大的样本具有有效性，在提高预测精度方面具有优越性。然而对于畸变特别严重的点，例如：2012年预测值相对误差有8%，还需要深入研究修正机理以提高精度。

[1]Erdal Kayacan，Baris Ulutas，Okyay Kaynak.Grey system theory-based models in time series prediction[J].Expert Systems with Applications，2010，37（2）：1 784-1 789.

[2]Kumar U，Jain V K.Time series models（Grey-Markov，Grey Model with rolling mechanism andsingular spectrum analysis）to forecast energy consumption in India[J].Energy，2010，35（4）：1 709-1 716.

[3]耿继进.灰色预测理论若干问题的研究[J].武汉测绘科技大学学报，1994，19（1）：57-62.

[4]张大海，江世芳，史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践，2002，22（8）：140-142.

[5]杨华龙，刘金霞，郑斌.灰色预测GM（1，1）模型的改进及应用[J].数学的实践与认识，2011，4（23）：39-46.

[6]李刚，黄同愿，闫河，等.公路交通事故预测的灰色残差模型[J].交通运输工程学报，2009，9（5）：88-93.

[7]蒋文伟，管宇，王祖良，等.灰色残差GM（1，1）模型在大气二氧化硫预测中的应用[J].浙江林学院学报，2002，19（2）：178-181.

[8]杨灿，杨敏华，汪齐松.基于灰色马尔科夫链预测系统的设计与实现[J].测绘科学，2009，34（6）：182-183.

[9]Hsu L C.Applying the Grey prediction model to the globalintegrated circuit industry [J]. Technological Forecasting and Social Change，2003,70（6）：563-574.

[10]夏秀峰，董彦军.基于改进马尔科夫模型的航空备件需求预测[J].兵工自动化，2013（11）：34-41，48.

[11].崔勇，王川，陈小龙，等.基于灰色马尔科夫预测模型的中长期电力负荷预测[J].现代电力，2011，28（3）：38-41.