基于数据挖掘技术的台区合理线损预测模型研究

2015-03-02邹云峰

电力需求侧管理 2015年4期

邹云峰，梅飞，李悦，程云，涂旺，梅军

（1.江苏省电力公司电力科学研究院，南京 210000；2.河海大学能源与电气学院，南京 211100；3.东南大学电气工程学院，南京 210096）

线损率作为一种综合反映电力系统中规划设计、生产运行、经营管理水平的经济技术指标，是电力部门日常管理工作中所关注的重要内容。降低线损率能够带来非常可观的经济与社会效益。我国对低压客户全面实行分台区管理，台区线损直接反映了一个地区的电网营销管理水平。台区线损管理通过比较理论线损与实际线损的差值，对不合理线损进行分析和预测，提供较为科学有效的降损措施，有利于提升电力部门的管理水平与经济效益，促进电网的建设与改造的科学性与合理性。

传统的台区线损管理中采取一刀切的方式，通过人工设定台区合理线损率，缺乏科学依据，也与精益化的管理目标背道而驰。实现台区合理线损的准确快速预测成为亟待解决的重要问题。传统对于理论线损的计算主要是包括基于潮流计算的方法[1—2]，神经网络[3—4]、支持向量机[5]、核心向量机[6]等及其他改进算法[7]。但是由于低压台区下分支线路复杂，元件多样，设备台账数据不全，理论线损计将非常困难，实时性不高。同时，台区线损数据庞大，以江苏省为例，全省台区多达40余万个，传统的理论台区线损计算将难以在低压台区线损评估中进行实际应用。

随着智能电能表的推广应用以及用电信息采集系统建设工作的快速推进，低压台区关口计量点和用户计量点实现远程准点抄表，极大提高了低压台区线损管理的实时性与准确性。江苏省电力公司从2013年开始基于用电信息采集数据进行低压台区线损管理，几年来，全省线损率在-1%至10%间的台区比重从65%提高到2014年底的91%，降损增效显著。随着电力改革的深入，如何进一步提高台区线损管理精益化水平，给出每个台区可参照的合理线损率范围，实现线损在线监控，指导并及时发现异常台区，分析原因，及时解决问题，成为电力营销工作迫切需要解决的问题。

近年来，随着用电信息采集系统的全面建设以及数据挖掘技术在电力系统中的广泛应用，利用数据挖掘技术深入发掘电力系统台区线损实时采集数据，找出其中蕴含的潜在规律，并应用于台区线损预测成为可能。文献[8]介绍了数据挖掘在线损计算中的实施；文献[9]提出用电量预测的多元回归模型并探讨了模型中相关参数检验。

本文的主要思想在于：特征相类似的台区应该具有较为近似的线损率，且通过线损治理大部分台区线损处于合理范围之内。因此，本文基于数据挖掘技术，首先通过聚类方法按照台区特征对海量的台区数据进行分类；其次，对每一类典型台区通过回归方式建立数学模型；最后将所要预测的数据输入模型，预测线损值。由于K均值（K-means）算法优点是可以处理大数据集[10]，具有很好的可伸缩性，很高的效率，简单快速，以及易于工程实现等特点，故本文采用了K-means聚类方法，尝试对电力营销与用电信息采集相关数据进行多维聚类分析，建立预测模型，并用某个月份的全省40多万个台区的数据进行了分析与验证，为在线线损评估系统的布置以及进一步改进算法提高预测精度提供标准和参考。

1 K均值聚类算法基本原理

作为一种硬聚类算法，K-means主要思想是：首先确定样本数据的聚类数K；接着任选K个数据作为初始聚类中心；然后每个数据按照欧氏距离大小置于与它最相似的类中；重新计算每个新类的平均值，并以此平均值作为新的聚类中心；反复迭代，直到满足收敛条件，即目标函数达到最小值。

欧氏距离定义为

式中：dij表示第i个样品xik与第j个样品xjk间的距离。dij越小，2个样本越接近。

目标函数通常采用平方误差准则

式中：E表示所有聚类对象的平方误差；xq为聚类对象；mi是类Ci的各聚类对象的平均值，其计算公式为

式中：|Ci|表示类Ci的聚类对象的数目。

聚类结果对孤立点和噪声点十分敏感，因此如果聚类结果中由某类数据相对于其它类数据可以忽略不计，那么应该剔除该类数据，重新聚类。

2 基于K均值聚类与线性回归的数据挖掘算法流程

2.1 算法基本流程

根据特征类似的台区拥有较为接近的线损率的原则，本文算法模型实际包含K-means聚类与线性回归2个部分。通过K-means聚类按照与台区线损率相关的基本特征属性分为K类，然后将每一类数据分别建立各自的线性回归模型，通过回归模型代入对应台区特征数据，得到预测的台区线损率，定义为合理线损率。合理线损与实际线损之差即为预测误差。算法的基本流程如图1所示。

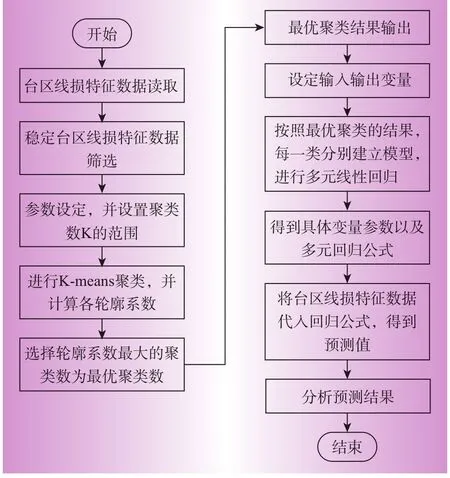
图1 基于K均值聚类与线性回归的算法流程

2.2 算法的具体步骤

（1）K-means模型建立：将原始数据输入到K-means聚类模型中，设定聚类数K为2—15。设定相应的输入输出变量。

（2）最优聚类结果的选择：计算得到聚类数为2—15的各聚类结果，通过比较轮廓系数确定最优聚类数，得到最优化的聚类结果。

（3）聚类结果的进一步优化：分析聚类结果，由于K-means聚类对噪声点和孤立点敏感，可能出现聚类结果中有的类的数据相对其他类的数据特别少的情况，可以剔除此类数据以重新聚类，提高聚类质量。

（4）回归模型建立：将生成的K类数据按照类别分别输入回归模型，设定回归的输入输出变量以及异常值容差，建立K个回归模型。

（5）回归方程生成及预测质量分析：通过K个回归模型得出K个回归方程；观察预测变量重要性，可将重要性很低的输入过滤以进行重新建模；分析生产模型的显著性结果，即Sig.指标；通过回归模型对输入数据进行预测验证，检验预测效果，并分析是否出现奇异点。

（6）测试数据代入相应类的回归公式中，得到预测结果，并分析评价线损预测结果。

3 数据挖掘算法在台区合理线损预测中的应用

本文将利用用户采集系统的实际采集数据，基于软件平台，对上述算法在台区合理线损预测中的应用进行验证。

3.1 K-means聚类模型及结果分析

以江苏省部分农网实际稳定台区数据为样本数据（共130 109个），作为聚类模型的输入。聚类样本特征输入量包括：总用户数、居民户数、非居民户数、居民容量、非居民容量、变压器容量、居民容量占比、居民户均容量、供电量。选择K-means聚类，初始聚类数设定为2—15。各聚类数对应的轮廓系数如表1所示。

表1 K-means轮廓系数比较

通过对轮廓系数的分析对比，可知在聚类数为3时，聚类质量最好，其对应的聚类结果分别如图2所示。

由图2可知，聚类数为3时，3类数据的占比分别为43.7%、41.7%、14.6%。聚类后样本数分别为56 875个、54 298个、18 936个。聚类后各变量均值如表2所示。

由表2可以看出，聚类-3居民容量占比为0.14，可以认为此类为非居民用户类。聚类-1和聚类-2居民容量占比分别为0.89和0.93，可以认为这2类为居民用户类，同时户均容量分别为5.15 kVA和8.34 kVA，可认为是2种不同规格台区（对应4 kVA与8 kVA）。可见，分类特征显著，具有较为明显的物理意义，K-means聚类结果较为合理。

图2 聚类数为3时聚类模型概要及聚类大小

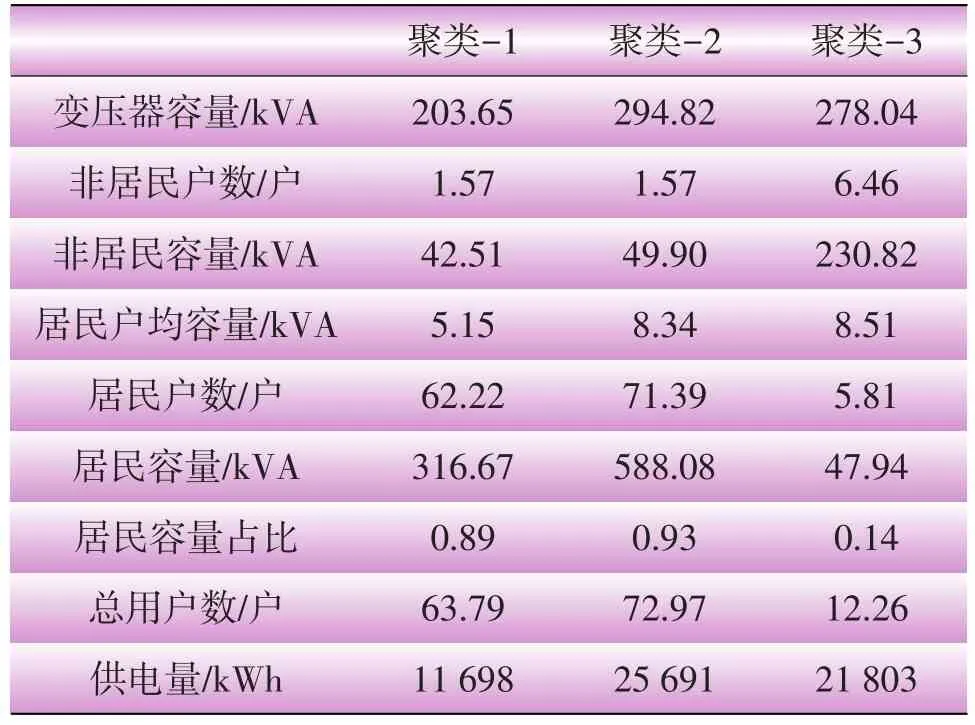
表2 最优聚类各聚类中心

3.2 多元线性回归模型

线性回归建模的思路是根据聚类数据结果，将3类数据分别作为线性回归模型的输入，以线损率作为输出，建立线性回归模型，并对结果做相应分析，并对出现的奇异点做具体分析。数据源是上述K-means聚类的3类数据：聚类-1、聚类-2、聚类-3。建模特征参数包括：用户总数、居民户数、非居民户数、居民户容量、非居民容量、居民户均容量、居民容量占比、变压器容量、供电量。输出参数为：线损率。异常值误差设定为1.0×10-4。表3所示为3个线性回归模型的相关系数。

3个模型的Sig.都小于0.000 5，非常显著，因此生成的模型均具有明显的统计学意义。图3至图5为预测线损率与实际线损率之间的预测误差直方图。

由图3—图5可知，实际线损和预测线损之差在0附近的占绝大多数，数据主要集中在[-1.5，1.5]，且不存在奇异点，残差符合正态分布，取得了良好的回归预测效果。图6—图8所示为3个回归模型的预测线损率与实际线损率散点图。图中实线A为预测线损和实际线损相等的点的集合，虚线B、C确定的区域为线损合格的区域（95%置信区间）。表4给出了3个模型95%置信区间的界限值。

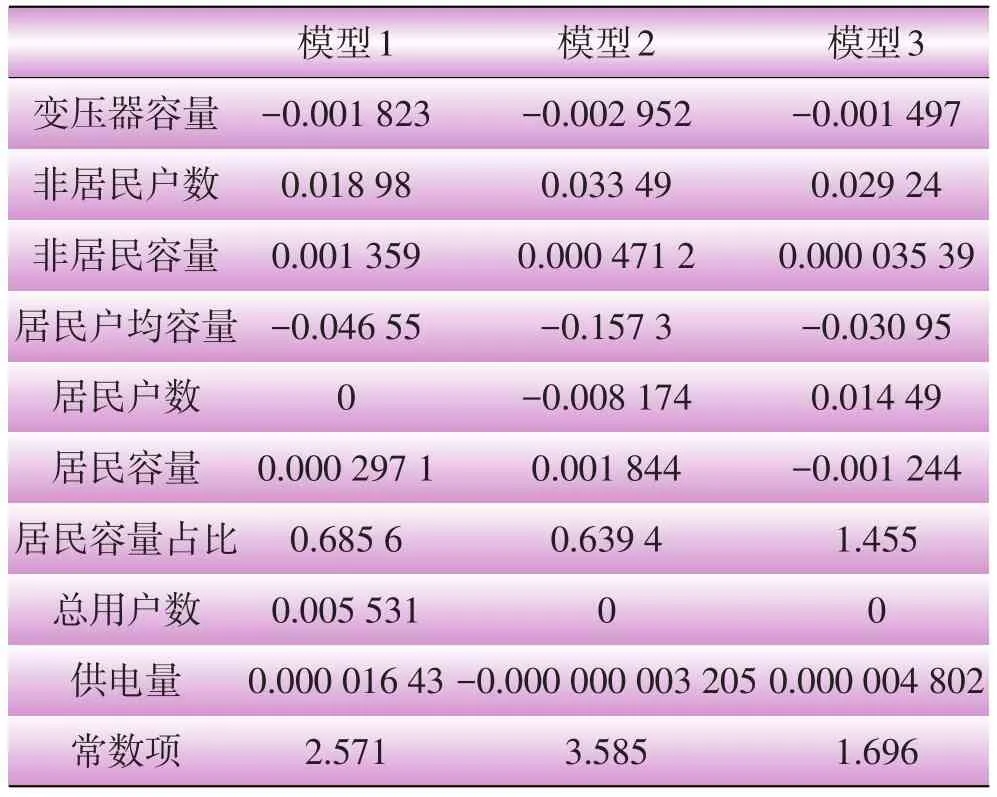
表3 3类线性回归模型系数

图3 模型1实际—预测线损率分布直方图

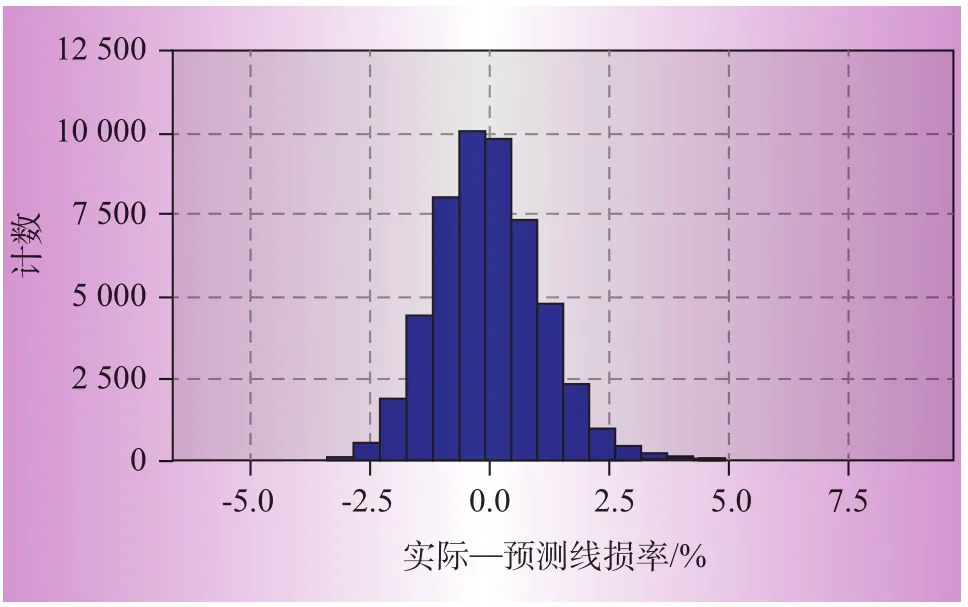
图4 模型2实际—预测线损率分布直方图

图5 模型3实际—预测线损率分布直方图

图6 模型1实际—预测线损率散点图

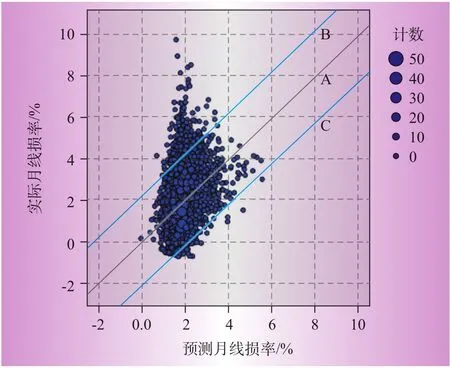
图7 模型2实际—预测线损率散点图

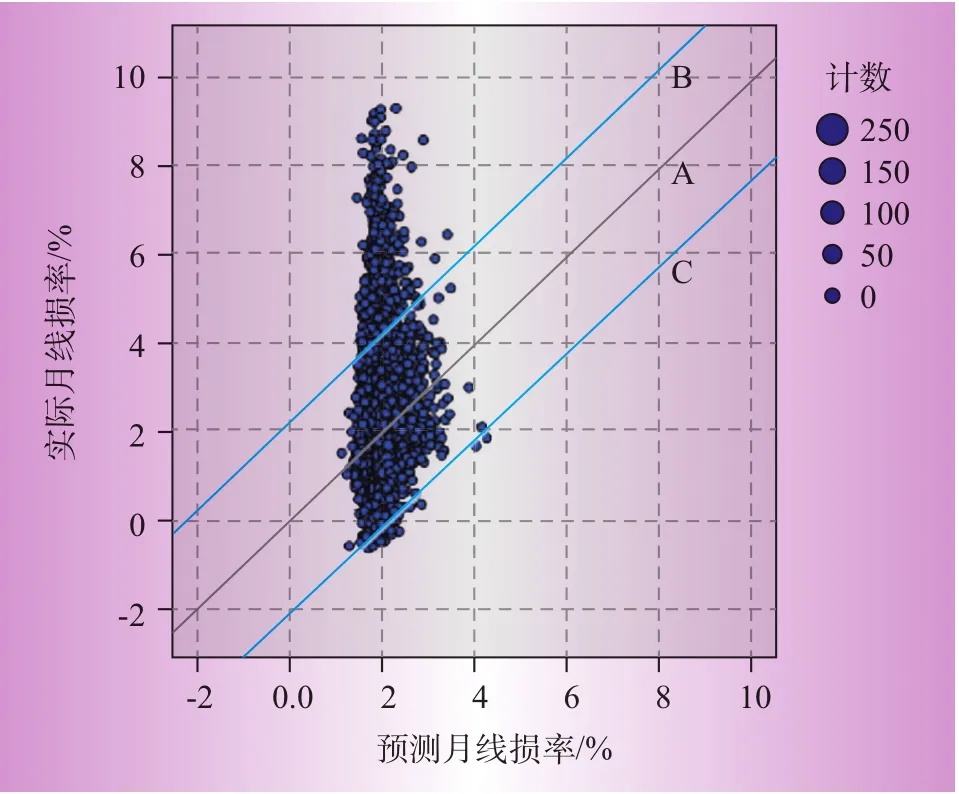
图8 模型3实际—预测线损率散点图

表4 95%置信区间对应的残差

3.3 数据测试结果

为验证图1中所述算法的有效性，本文利用线性回归模型对高淳、金坛两地的采样数据分别进行了回归预测，采用欧氏距离来判别测试样本的类别属性，即计算测试样本与3个聚类中心的距离，取最短距离的类别作为测试样本的类别属性，也就是说，采用该类别的回归方程。表5表示为3类测试样本线损率预测绝对误差在2.5%以上的台区数目。

表5 测试样本预测误差

本文认为预测偏差较大意味着台区线损不合理，同时也对预测误差较大的样本进行了进一步的分析比较。以模型1中的数据为例，经查预测误差超出范围的样本数为680个，其中实际测量线损值超过10%的台区143个，小于-1%的台区76个，这部分台区属于需要进行整改的台区；实际测量线损值在5%～10%区间内的台区共229个，这些台区需要进一步深入考察，确定是否具有提升的空间；剩余样本231个，这部分样本属于实测线损合格，但预测值与实际值存在差异，需要重点加强监测，确认误差来源于表计误差还是建模误差，以提升建模精度。