基于改进PSO算法的Logistic模型在饱和负荷预测中的应用
2015-03-02邹品晶左郑敏欧阳旭朱向前姚建刚
林 勇,邹品晶,左郑敏,欧阳旭,朱向前,姚建刚
(1.广东电网公司 电网规划研究中心,广州 510080;2.湖南大学 电气与信息工程学院,长沙 410082;3.广东电网发展研究院有限责任公司,广州 510080)
饱和负荷是近年来电网规划中提出的新概念,他体现着一个区域负荷发展的最终规模[1,2]。研究饱和负荷对于电力工业的规划和发展,特别是电网 的建设和改造具有重要的指导意义。
区域电力负荷整个过程的增长大致呈如下变化:负荷开始增长比较缓慢,随后将经过一段时期的较快增长,之后进入低速平缓增长阶段,最后达到一个整体饱和状态[3]。Logistic曲线一般可分为4段,可以分别解释为初始发展阶段、快速发展阶段、后发展阶段和饱和发展阶段,其中曲线初始发展阶段增长较慢,快速发展阶段将以较快速度增长,后发展阶段又趋向于较慢速度增长,饱和发展阶段将以较小幅度在某一极限值附近上下波动[4—7],这一特点与电力负荷的增长规律有相似之处,因此将Logistic曲线模型应用于饱和负荷预测具有一定的可行性。Logistic时间序列饱和负荷预测的一大关键在于如何确定曲线模型中的各个参数值,本文在研究最新智能算法的基础上,将粒子群优化算法(particle swarm optimization,PSO)应用到Logistic时间序列饱和负荷预测中,用于求解曲线模型中的各个参数。
基本PSO算法具有依赖的经验参数较少、收敛速度快等优点,但也存在易陷入局部极值、收敛精度不高的缺陷[8,9]。本文对基本PSO算法进行改进,并将改进算法应用于Logistic时间序列饱和负荷预测,实现了对曲线模型参数的优化求解。通过实例分析可知,改进措施不仅使基本PSO算法收敛速度得到提高、局部容易陷入最优问题得到改善,而且证明了该改进PSO算法应用于Logistic时间序列饱和负荷预测的可行性。相对于基本PSO算法和Marquardt迭代算法的参数寻优,基于该改进算法的Logistic模型拟合精度更高。
1 粒子群优化算法
PSO算法是由Eberhart和Kennedy于1995年提出的一类基于群智能的随机优化算法[10,11],他通过粒子间的相互作用,对解空间进行智能搜索,最终得到最优解。
假设在一个D维的目标搜索空间中,有N个粒子组成的一个群落,其中第i个粒子代表一个D维向量xi=(xi1,xi2,…,xid),即第i个粒子在D维搜索空间的位置。将xi代入目标函数即可以算出其适应值,最优解由适应值的大小而决定,第i个粒子的“飞行”速度也是一个D维向量,记为vi=(vi1,vi2,…,vid)。将第i个粒子至第t次迭代为止搜索到的最优位置为Pi=(Pi1,Pi2,…,Pid),整个粒子群至第t次迭代为止搜索到的最优位置为Pgd=(Pi1,Pi2,…,Pid)。算法的基本公式为

式中:c1、c2是正的学习因子,或称加速常数;r1、r2为0到1之间均匀分布的随机数;w为惯性因子,是控制速度的权重。
另外,通过设置微粒的速度区间[vmin,vmax]和位置范围[xmin,xmax],可以对微粒的移动进行适当的约束。基本PSO算法操作简单,使用方便,收敛速度较快,但是在算法后期,粒子群中所有粒子都将聚集到一个极值点附近,此时Pid、Pgd与xid相差很小,因此基本PSO算法存在以下缺点:①粒子都是根据全体粒子和自身的搜索经验而向最优解的方向“飞行”,在较大的惯性因子作用下,粒子有可能会缺乏对最优解的精细搜索而导致搜索精度不高;②所有粒子都向最优解方向“飞行”,越接近最优粒子,其速度越小,所以粒子群趋向同一,失去粒子间解的多样性,因而易于收敛到局部最优。
2 粒子群优化算法的改进
2.1 平均粒子浓度选取初始种群
初始粒子群的选取是随机的,理想状况下粒子位置分布应较为分散,以防止群体在某一区域内过度集中。保持群体的多样性有利于寻优搜索遍布整个解空间,从而增加搜索到全局最优解的概率。但是粒子的个数是有限的,解空间又相对较大,为了保证有限个粒子能够均匀地分布在整个解空间,保持群体的多样性,避免陷于局部最优的可能,引入平均粒子浓度

平均粒子浓度表示种群的多样性好坏,α(t)越高表示种群中非常类似的个体大量存在,不利于全局优化,可以设定平均粒子浓度阈值ε=0.001,对于随机产生的粒子,其平均粒子浓度应不大于ε,从而达到保持种群个体多样化的目的。
2.2 动态改变惯性权值
惯性权重w影响微粒的局部最优能力和全局最优能力。较大的w有利于提高算法的全局搜索能力,而较小的w会增强算法的局部搜索能力,选择一个合适的w可以平衡全局和局部搜索能力,这样可以以最少的迭代次数找到最优解。常见的不同权重变化公式有线性递减权重、自适应权重、随机权重算法等[13,14],本文采用动态改变惯性权重的方法为
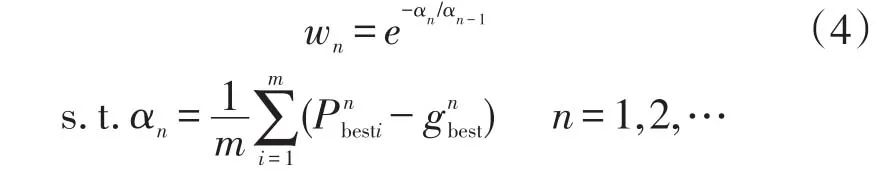
式中:wn为第n次迭代时的惯性权值;为第i个粒子在第n次迭代时找到的最佳适应度值;表示整个群体在第n次迭代时找到的最佳适应度值。
计算αn指标是用来判断目标函数的平整度,如果αn较大,则目标函数的平整性较差,每次迭代时αn指标都根据所得适应度值进行变化,这样使w变成随搜索位置改变而动态改变的wn,搜索方向的启发性增强。不同迭代次数中的-αn/αn-1比值变化过大,采用工程中常用的e作为指数来降低其变化幅值,以改善wn的平滑性。αn的减小幅度越快,说明趋向极值点的速度越快,此时wn也就较大,便于保持大步长的搜索;当接近极值点时,αn每次的变化减小,此时wn也就较小,以便于在极值点附近作小步长搜索,有利于避免局部收敛。
2.3 对不活跃粒子施加扰动
粒子群算法易出现“早熟”现象,当“早熟”现象发生时,对不活跃粒子施加扰动以重新激活粒子,使其离开局部极值点。可以假设第k次迭代过程发生“早熟”,则需要对第k+1次迭代中进行扰动

可以定义寻优过程出现“早熟”的条件为
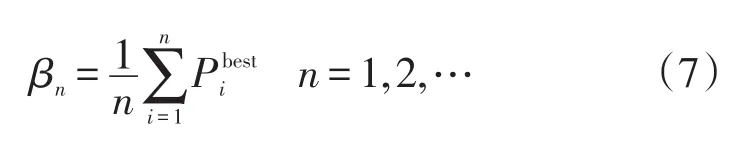
迭代过程中,当(βn-βn-1) <0.001连续出现G=4代时,可以认为整个粒子群出现“早熟”现象,此时需要对出现“早熟”的粒子施加扰动,使其离开局部极值点。
3 Logistic模型在饱和负荷预测中的应用
3.1 Logistic时间序列饱和负荷预测模型
以年电力负荷为准构建Logistic饱和负荷预测模型。记yt(t=1,2,…,L)为第t年的实际电力负荷值,Logistic饱和负荷预测值为

负荷增长率的表达式为

令公式(9)等于2%[15],可以得到饱和年tL,S,代入公式(8)即得到饱和负荷预测值。
若以平均绝对值相对误差最小为目标,则问题转化为

只要求出式(10)中的最佳系数c,b,a,则可计算出各年度Logistic模型预测值,使曲线拟合误差较小,从而实现更精准的饱和负荷预测。
3.2 误差评价指标
本文选取平均绝对值相对误差EMAPE和均方根相对误差EMSE作为预测效果评判的根据。
其中,平均绝对值相对误差
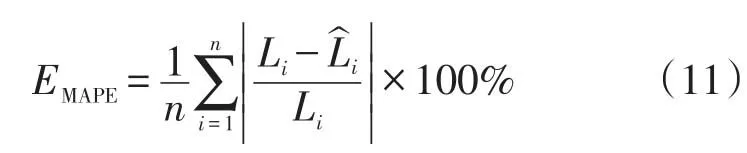
均方根相对误差

式中:L、Li分别为实际负荷和预测负荷;n为历史负荷数据的个数。
4 改进PSO算法的Logistic模型在饱和负荷预测中的应用
4.1 改进PSO算法的基本参数设定
本文中改进PSO算法寻优搜索对象为Logistic函数模型参数c,b,a,根据某地区电网全社会用电量历史数据,可以设定粒子群优化算法的搜索范围为:0≤c≤6 000,0≤b≤200,0≤a≤1,粒子数N取50,粒子数目越多,在确定的优化范围内分布就越广,不易陷入局部最优,能够提高算法全局搜索能力,但是算法收敛速度会变慢,所以粒子数目设置应该根据具体问题而定。最大迭代次数Tmax取500。惯性权重系数初值w0=2.728 9,开始时较大的惯性权重系数能够保持较强的全局搜索能力,随着迭代的进行,按照式(4)更新w的值,显然易知其值将逐渐减小,即其局部搜索能力会增强。加速常数c1和c2代表将每个粒子推向Pbesti和gbest位置加速项的权重,加速常数c1较大时,会使粒子过多的在局部范围徘徊,而c2较大时会促使粒子过早收敛到局部最小值,为了平衡随机因素的作用,取c1=c2=2,平均粒子浓度阈值ε=0.001,采用平均粒子浓度来描述种群分布的多样性,指导初始种群的选取,以提高整体寻优质量,对于随机产生的粒子,其平均粒子浓度应不大于ε。
4.2 改进PSO算法的Logistic时间序列饱和负荷预测过程
基于改进PSO算法的Logistic模型在饱和负荷预测中应用的流程图如图1所示。
具体实现步骤如下:
(1)按照前文所述方法初始化种群,设定种群规模N和粒子位置和速度的约束边界,惯性权重初值w0,加速常数c1,c2,最大进化迭代次数Tmax和阈值ε。
(2)判断产生的种群是否满足约束条件,若不满足,转(3);否则,按照式(3)计算种群的平均粒子浓度α(t),判断α(t)≤ε是否成立,若不成立,转(3);否则,转(4)。
(3)重新初始化粒子群。
(4)根据当前位置计算各个粒子的适应度函数值并作比较,将第i个粒子当前点设为最优位置Pbesti,所有粒子中最优者设为种群最优位置gbset。
(5)判断是否达到最大迭代次数Tmax,若是则结束寻优,得到最优解,转(12);否则,转(6)。
(6)判断迭代次数t=1是否成立,若是则转(7);否则,转(8)。
(7)更新惯性权值,并更新每个粒子的位置和速度,转(9)。
(8)利用式(7)判断是否出现不活跃粒子,若没有出现转(7);否则,判断不活跃粒子是否出现G代,若不是转(7);否则,利用式(5)和式(6)对不活跃粒子施加扰动。

图1 改进PSO算法的Logistic模型在饱和负荷预测中应用的流程
(9)判断更新的粒子是否满足约束条件,若满足,转(10);否则,按照初始化标准更新每个不满足约束条件粒子的位置。
(10)计算各粒子适应度函数值,并分别与其历史最优位置Pbesti和种群的历史最优位置gbset的适应度函数值作比较,若更优,则替换;否则,保持不变。
(11)t=t+1,转(5)。
(12)将寻优结果c、b、a赋给Logistic曲线模型,进行饱和负荷预测。
5 实例分析
为验证本文改进PSO算法的Logistic模型应用到饱和电力负荷预测中的正确性和可靠性,本文利用某地区电网1970—2012年间主要年份的全社会用电量数据进行预测验证[16]。分别采用基本PSO算法、改进PSO算法和Marquardt迭代法对Logistic模型进行参数寻优,其中基本PSO算法、改进PSO算法相关参数按照4.1节中的要求设置。Marquardt迭代法寻优使用软件中Marquardt迭代算法进行,最大迭代次数Tmax=500,寻优结果如表1。
从表1可以看出,改进的PSO算法迭代次数为46次时,适应度函数已趋向于稳定,而PSO算法和Marquardt迭代法分别需要80次和50次迭代,说明改进的PSO算法拥有更好的收敛速度。

表1 3种寻优算法的寻优结果
图2为改进PSO算法与PSO算法迭代过程中适应度函数值的变化情况。从图2中可以看出,改进PSO算法不仅比PSO算法提前收敛,而且稳定时适应度函数值也更小。从3.1节可以得知适应度函数值越小,曲线拟合误差越小,可见改进的PSO算法在收敛速度和精度上都要优于PSO算法,算法改进效果较好。

图2 改进PSO算法与PSO算法适应度函数值比较
将上述3种算法的寻优结果代入式(8),并对算例中全社会用电量历史数据进行拟合,拟合结果与误差分别如表2和表3所示,3种方法拟合曲线如图3所示,其中A1、A2和A3分别代表PSO算法Logistic拟合模型、改进PSO算法Logistic拟合模型和Marquardt迭代法Logistic拟合模型。
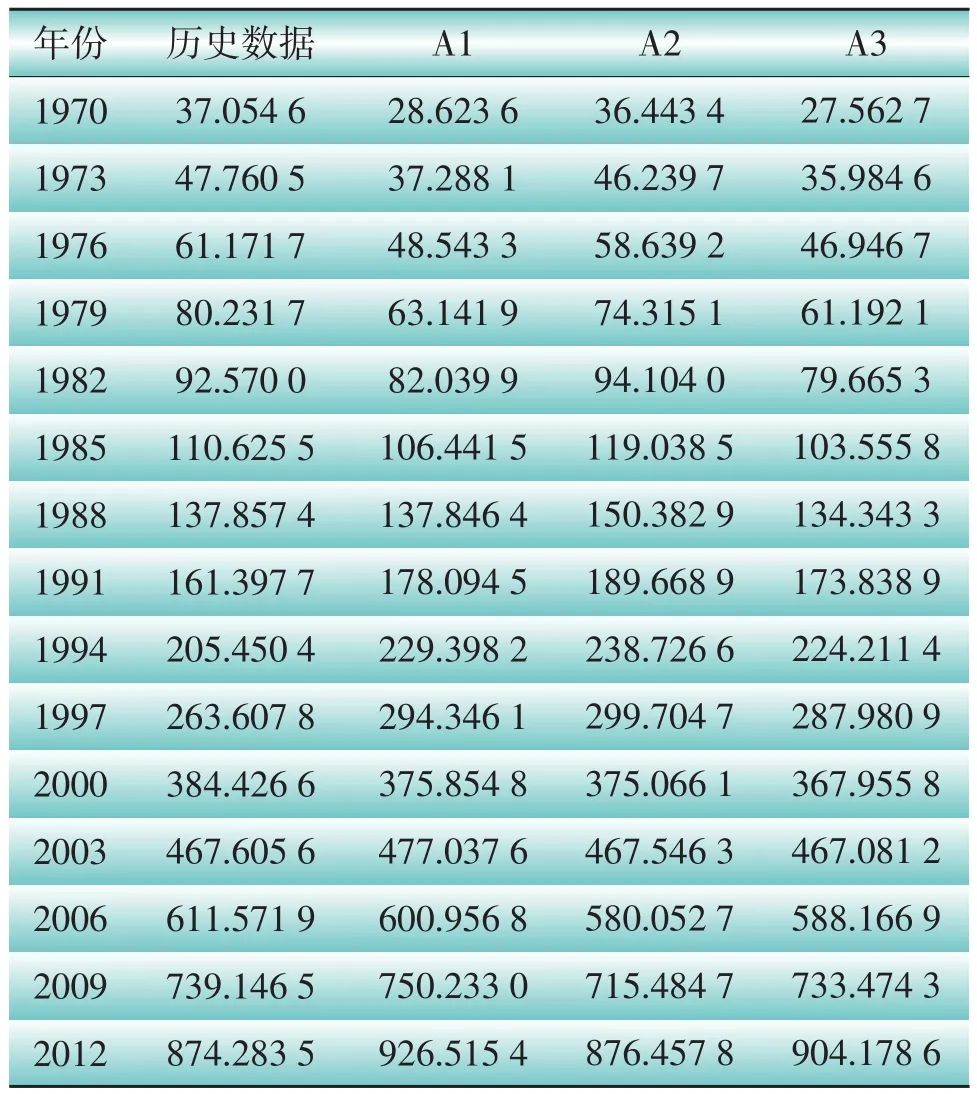
表2 3种预测模型全社会用电量拟合结果亿kWh

图3 3种方法的全社会用电量拟合曲线
由表2和表3可以看出,改进PSO算法的Logistic拟合模型的平均绝对值相对误差、均方根相对误差2项误差分析指标分别为6.210 3%和8.274 4%,满足长期负荷预测误差要求,且优于其他模型,从图3可以直观看出改进PSO算法的Logistic拟合模型的优越性。将本算例中由改进PSO算法得到的最佳系数c、b、a代入Logistic模型,再令公式(9)等于2%,可得到该地区电网全社会用电量的饱和年份为2045年,回代即可得其饱和全社会用电量为3 828.002 6亿kWh。
以上分析运用了基于改进PSO算法的Logistic模型预测某地区电网的饱和全社会用电量。当该模型能较好地拟合历史数据时,通过一定计算可得到该地区电网饱和年份和饱和全社会用电量。但是,由于未来的预测结果难以验证,为了证明该预测结果可信,将采用人均用电量法进行预测,以形成对比验证。人均用电量法是目前较为成熟的饱和负荷预测方法[17],人口和人均用电量都具有S型变化趋势,此处不妨采用Logistic模型进行分析与拟合,得到其拟合方程如表4所示。

表3 预测模型的百分比误差比较

表4 人口和人均用电量拟合方程
从表4可以看出,2个拟合模型的拟合优度R2都十分接近于1,而拟合优度是对回归模型拟合程度的综合度量,且取值范围在0到1之间,当拟合优度越大时,说明其拟合效果较好。结合以上分析,并将饱和条件仍然设定为全社会用电量增长率为2%,人均用电量法的具体预测和分析过程不再赘述,通过一定的分析与计算可得到基于改进PSO算法的Logistic模型与人均用电量法预测结果对比如表5所示。

表5 基于改进PSO算法的Logistic模型与人均用电量法预测结果
从表5可知,该地区电网饱和全社会用电量在3 041.315 1亿~3 828.002 6亿kWh之间,饱和年份大致在2044或者2045年。
6 结束语
本文分析了基本PSO算法及其存在的缺点,并对原算法进行相应的改进,最终运用该改进算法对Logistic时间序列预测模型的参数c、b、a进行反复迭代寻优,得到最优粒子对应的曲线参数组合,建立了基于该优化算法的Logistic时间序列饱和负荷预测模型,利用该模型拟合某地区电网1970—2012年间主要年份的全社会用电量,算例表明:基于改进PSO算法的Logistic模型较好地拟合了该电网历史电量数据,说明该模型能够很好地反映电力负荷整体变化趋势。另外,运用该方法和人均用电量法分别对该地区电网饱和全社会用电量进行了分析和预测,得到了较为相近的结果,考虑到人均用电量法是现今较为成熟的饱和负荷预测方法,从而间接证明该优化算法应用于饱和电力负荷预测是可行的。
但是,该方法也存在一定的缺陷,比如:①模型很难根据未来的情况变化做出及时的调整;②未能将影响负荷的多方面因素都系统的考虑进去。鉴于以上问题的存在,想要更精确地分析和预测饱和,则需要采取更科学、合理的方法。伴随人工智能、系统动力学等方法逐渐应用于饱和负荷分析,饱和负荷预测研究将更加深入。
[1]崔凯,李敬如,刘海波,等.城市负荷饱和阶段电力规划方法及其在济南电网中的应用[J].电网技术,2007,31(2):24-26.
[2]崔凯,张丽娟,李敬如,等.天津市中心城区饱和负荷分析与预测[J].电力技术经济,2008,20(5):32-36.
[3]肖欣,周渝慧,张宁,等.城市电力饱和负荷分析技术及其应用研究综述[J].电力自动化设备,2014,34(6):146-152.
[4]葛雄灿,胡秉民,高毅.最优组合预测方法及其在Logistic曲线与Gompertz曲线之综合拟合中的应用[J].浙江农业大学学报,1998,24(4):443-446.
[5]Coyle J J,Bardi E J,Langley C J.The Management of Business Logistics(6th Edition)[M].West Publishing Company,1996:9-25.
[6]Babcock,M W,Lu X,Norton J.Time series forecasting of quarterly railroad graincarloadings[J].Transportation Research,Part E:Logistics and Transportation Review,1999,35(1):43-57.
[7]洪露.电网发展的阶段性研究及启示[D].浙江:浙江大学,2013:56-59.
[8]李鑫滨,马阳,鹿鹭.一种基于校正因子的自适应简化粒子群优化算法[J].燕山大学报,2013,37(5):453-458.
[9]师彪,李郁侠,于新花,等.自适应变系数粒子群——径向基神经网络模型在负荷预测中的应用[J].计算机应用,2009,29(9):2 454-2 458.
[10]Kennedy J,Eberhart R C.Particle Swarm Optimization[C]∥IEEE Int.Conf.on Neural Networks Perth,Australia,1995:1 942-1 948.
[11]Eberhart R C,Kennedy J.A New Optimizer Using Particle Swarm Theory[C]∥The Sixth International Symposium on Micro Machine and Human Science,Nagoya,Japan,1995:39-43.
[12]周刚,王洪斌.基于粒子群优化算法的输变电设备检修优化[J].南方电网技术,2013,7(3):109-112.
[13]王启付,王战江,王书亭.一种动态改变惯性权重的粒子群优化算法[J].中国机械工程.2005,16(11):945-948.
[14]张选平,杜玉平,秦国强,等.一种动态改变惯性权重的自适应粒子群算法[J].西安交通大学学报,2005,39(10):1 039-1 042.
[15]尚芳屹.组合预测在区域级饱和负荷预测中的应用[D].上海:上海交通大学,2013:15-16.
[16]郭栋,李冲.北京统计年鉴—2013[M].北京:中国统计出版社,2013:110-111.
[17]王伟,房婷婷.人均用电量法在区域饱和负荷预测中的应用研究[J].电力需求侧管理,2012,14(1):21-23.
