基于贪婪策略整体分布优化算法的0－1背包问题求解

薛翠平，刘静宜，肖 冬

（1.东北大学理学院，辽宁 沈阳110004；2.东北大学信息科学与工程学院，辽宁 沈阳110004）

0 引言

20世纪50年代末，Daunts首次提出0－1背包问题（Knapsack problem），它是一类非常经典的Np问题［1］，在实际生活中，网络资源分配问题、调运装载、生产安排、信息加密等问题都能建出0－1背包问题的数学模型［2－4］，因此对该问题的研究在理论上和现实中都具有重要的意义.

0－1背包问题可以简单描述为：给定n种物品集合N＝｛1，2，…，n｝和一背包.已知物品i的质量为wi（＞0），价值为vi（i＝1，2，…，n），背包容量为c.求最优装包方案（x1，x2，…，xn），xi∈｛0，1｝（xi＝0表示不把第i个物品放入背包，xi＝1表示把第i个物品装入背包），使背包获得的价值达到最大.在选择装包物品时，不能将物品装入背包多次，也不能将物品分割装入，数学模型如下：

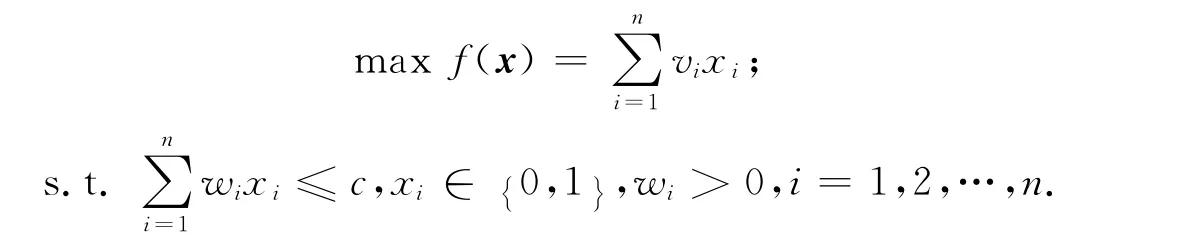
许多学者对该问题进行了行之有效的研究，主要包括适用于小规模问题的分支限界法、递归法、回溯法、动态规划法等及适用于大规模问题的智能计算方法（遗传算法、人工鱼群算法、模拟退火算法、粒子群算法、免疫算法等［5－8］）.目前这方面的文献很多，每种方法各有优劣，但总体来说思想还是比较复杂.

1 算法

整体分布优化算法是粒子群优化算法衍生出来的一种新智能优化算法［9］，本文将贪婪思想嵌入到整体分布优化算法中，得到基于贪婪策略的整体分布优化算法.该算法主要具有结构简单、实现容易、代码较少和参数少的优点.种群相对价值较高，程序对内存要求较小，种群的个体可以逐一形成，不需要存储.算法的基本思想是首先在定义域范围内随机产生一个初始种群，在种群中找到最优粒子，然后直接在最优粒子附近由柯西分布产生新的种群，周而复始，直到达到最大的迭代次数为止.决定该算法性能的因素主要产生种群的概率分布形式及其参数的选取，算法的收敛策略及其对应参数的选取.根据贪婪思想，将所有物品按照价值密度（每种物品的价值系数vi与其质量wi的比值）从大到小编号.将相应的vi和wi按照价值密度顺序大小做相应的调整.新的问题记为：

以下内容是在新问题的基础上求解的：首先，整体分布式优化算法需要编码，在0－1背包问题中只存在装入和不装入2种情况，所以算法采用二进制编码，0表示不装入，1表示装入，编码长度为所需装入物品的数量；其次，整体分布优化算法需要适应度函数，这里我们把适应度函数定义为0－1背包问题的目标函数

整体分布优化算法的初始种群通过下面的子算法1给出.

算法1 初始种群的产生，种群规模为m，变量的维数为n

Step 2 将第一步产生的解转换成可行解，思想为贪婪思想，即尽量将下角标小的物品装入背包.比如，当前已经考虑到第k个物品，若x［i］［k］＝0，则第k个物品不装入背包；若x［i］［k］＝1，考虑将第k个物品装入背包，看看是否超重，若不超重，则装入，否则，该物品不应装入背包，置x［i］［k］＝0.

下面给出完整的整体分布式优化算法.

算法2 贪婪策略整体分布优化算法

Step 1：初始化.在整个定义域内按照子算法1产生初始种群，同时初始化柯西分布的半径为覆盖整个定义域的0.5倍，初始化参数.柯西分布尺度参数γ＝0.1，种群直径递减率α＝0.93，停滞次数β＝9，最大迭代次数10 000或者种群直径的标度小于0.000 001，种群的规模为70.

Step 2：计算种群中每个个体的适应度值，找出本次最好的个体并与上次的最好个体比较，如果好于上次，则进行替换，种群的直径保持不变.

如果差于上次的最好个体，则保留上次，同时使停滞次数减1，若停滞次数为0，则使种群直径缩减为原来直径的0.93，同时使停滞次数变为9；若停滞次数不为0，则保持原来的种群直径不变.迭代次数减1.

Step 3：以已经找到的最好个体的坐标为中心，用柯西分布产生新的种群.

Step 4：如果当前迭代次数达到了预先设定的最大次数或种群直径的标度小于0.000 001，则停止迭代、输出最优解、否则转到Step 2.

2 实例

为了验证本文算法在求解0－1背包问题上的有效性，这里引用文献［7］中的3个实例，3个例子的规模从小到大倍增，通过3个实例比较了几种算法结果的优劣及本文算法点列的收敛趋势及速度.

例1 物品个数n＝20，物品价值集合P＝｛92，4，43，83，84，68，92，82，6，44，32，18，56，83，25，96，70，48，14，58｝，物品质量 集 合W ＝｛44，46，90，72，9l，40，75，35，8，54，78，40，77，15，61，17，75，29，75，63｝，背包容量C＝878，具体结果见表1和图1.

表1 例1中7种算法的最好结果对比

例2 物品个数n＝50，物品价值集合P＝｛220，208，195，192，180，180，165，162，160，158，155，130，125，122，120，118，115，110，105，101，100，100，98，96，95，90，88，82，80，77，75，73，72，70，69，66，65，63，60，58，56，50，30，20，15，10，8，5，3，1｝，物品质量集合W ＝｛80，82，85，70，72，70，66，50，55，25，50，55，40，48，50，32，22，60，30，32，40，38，35，32，25，28，30，22，25，30，45，30，60，50，20，65，20，25，30，10，20，25，15，10，10，10，4，4，2，1｝，背包容量C＝1 000，具体结果见表2和图2.

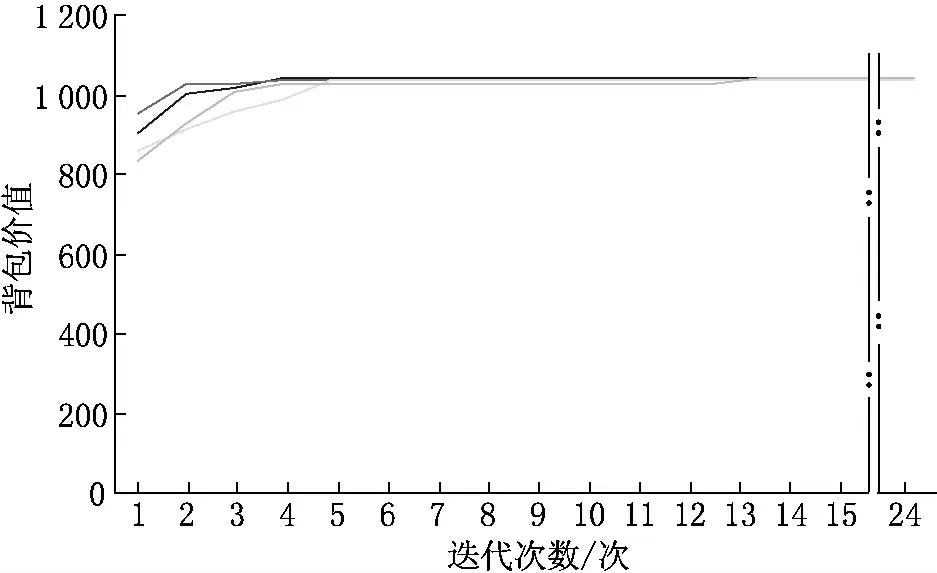
图1 例1中本文算法1次执行过程不同初始点向最优点收敛图形

表2 例2中7种算法的最好结果对比

例3 随机产生的实例，n＝100，物品价值集合P＝｛68，101，125，159，65，146，28，92，143，37，5，154，183，117，96，127，139，113，100，95，12，134，65，112，69，45，158，60，142，179，36，43，107，143，49，6，130，151，102，149，24，155，41，177，109，40，124，139，83，142，116，59，131，107，187，146，73，30，174，113，9l，37，168，175，53，151，125，31，192，138，88，184，110，159，189，147，31，169，192，56，160，138，84，42，151，37，21，22，200，85，135，200，139，189，68，94，84，22，18，115｝，物 品 的 质 量 集 合W ＝｛42，35，70，79，63，6，82，62，96，28，92，3，93，22，19，48，72，70，68，36，4，23，74，42，54，48，63，38，24，30，17，9l，89，4l，65，47，91，71，7，94，30，85，57，67，32，45，27，38，19，30，34，40，5，78，74，22，25，7l，78，98，87，62，56，56，32，5l，42，67，8，8，58，54，46，10，22，23，7，14，l，63，11，25，49，96，3，92，75，97，49，69，82，54，19，1，28，29，49，8，11，14｝，背包容量C＝2 010，具体结果见表3和图3.

表3 例3中7种算法的最好结果对比

图2 例2中本文算法1次执行过程不同初始点向最优点收敛图形

图3 例3中本文算法1次执行过程不同初始点向最优点收敛图形

由表1—3可以看出，本文基于贪婪策略整体分布优化算法对3个算例求解的最好结果与最优解优于其他几个算法.由图1—3又可以看出本文算法向最优点收敛的速度非常快.

3 结论

本文程序都是用C＋＋语言编写，每个实验均从不同的随机初始种群运行10次，整体分布优化算法与其他算法相比，取得了较好的效果，不但取得了最好的优化效果，而且优化结果非常稳定，每次优化结果的值变化不大.说明整体分布优化算法对0－1背包问题是可行的，为有效求解此类问题提供了一种新的可行方法，同时也拓展了整体分布优化算法的应用领域.

［1］SYSLO M M.Discrete optimization algorithm［M］.New Jersey：Prentice－Hall，1983：118－165.

［2］SOOJEONG CHOI，SUNJU PARK，HAK－MAN KIM.The application of the 0－1knapsack problem to the load－shedding problem in microgrid operation［J］.Communications in Computer and Information Science：Control and Automation，and Energy－System Engineering，2011，256（1）：227－234.

［3］NAONORI KAKIMURA，KAZUHISA MAKINO，KENTO SEIMI.Computing knapsack solutions with cardinality robustness［J］.Lecture Notes in Computer Science Algorithms and Computation，2011，7074：693－702.

［4］LAIH C S，LEE J Y，HAM L，et.A linearly shift knapsack public－key cryptosystem［J］.IEEE Journal Selected Areas Communication，1989，7（4）：534－539.

［5］秦玲，白云，章春芳，等.解0－1背包问题的蚁群算法［J］.计算机工程，2006，3（6）：212－214.

［6］沈显君，王伟武，郑波尽，等.基于改进的微粒群优化算法的0－1背包问题求解［J］.计算机程，2006（18）：23－24，38.

［7］王秋芬，梁道雷.一种求解0－1背包问题的启发式遗传算法［J］.计算机应用与软件，2013，30（2）：33－37，57.

［8］贺毅朝，刘坤起，张翠军，等.求解背包问题的贪心遗传算法及其应用［J］.计算机工程与设计，2007，28（11）：2655－2657.

［9］余炳辉.整体分布优化算法研究及应用［M］.成都：西南交通大学出版社，2012：129－140.