Kuramoto－Svashinsky方程的数值方法

张 俊， 范馨月

（1.贵州财经大学数学与统计学院，贵州 贵阳550025；2.贵州大学理学院，贵州 贵阳550025）

1 研究背景及现状

K－S方程是许多物理现象中出现的一类重要的数学物理方程，实际研究中经常能发现这一模型的应用.例如，等离子物理、热传导、氧化反应扩散、动力学、自由膜的流动等问题.方程具有内在稳定性与不稳定性的相互作用，从而表现为系统耗散性的典型无穷性动力系统.K－S方程已被认为是无穷维动力学中几个具有代表性的模型之一，其动力特性具有相当的普适性.而数值解的研究成为研究这类模型的主要内容之一.众多学者都研究过K－S方程的数值方法.［1－15］空间方向的离散主要有谱方法、有限差分、或有限体积法，时间方向采用的方法包括Runge－Kutta法［1－2］、指数形Runge－Kutta法［10］、Strang分裂方法［5－6］、隐式－显式方法［12－14］.一方面，显式多步法或者Runge－Kutta法在全离散的情况下通常是不稳定的或者条件稳定的.另一方面，隐式法大多是无条件稳定的，但在实际的计算中每一步要解一个非线性方程组；隐式－显示方法虽然是局部稳定的，但是在实际计算中时间步长要取得足够小.

本文构造了几种线性化半离散数值格式，并分析了该格式的稳定性.尽管我们没有给出误差估计，但是数值试验的结果显示了格式的有效性.最后的数值例子讨论解的混沌、周期等性质.

2 Kuramoto－Svashinsky方程

这里ν是非负常数，T 表示时间.

关于方程的连续解我们有如下的稳定性的结果：

引理2.1 方程（2.1）—（2.2）的解u满足不等式

其中

证明 方程（2.1）两边与u做内积，可得

由Young's不等式有

因此

令

则有

两边对t积分可得（2.4）式.

3 有限差分时间离散格式

在这里介绍K－S方程三个线性化的时间半离散格式，并考察其稳定性.对于一个给定的正整数K＞0，令tn＝nΔt，n＝0，1，…，K，这里时间步长Δt＝T／K.

Euler格式 考虑如下基于Euler方法的一阶半隐格式：

引理3.1 对所有un∈H1＊（Λ），有（2un∂xun＋1＋un＋1∂xun，un＋1）＝0.

证明

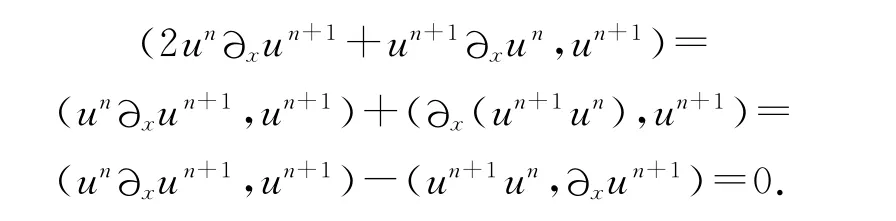
引理得证.

引理3.2 对所有网格函数｛ un｝ ，有

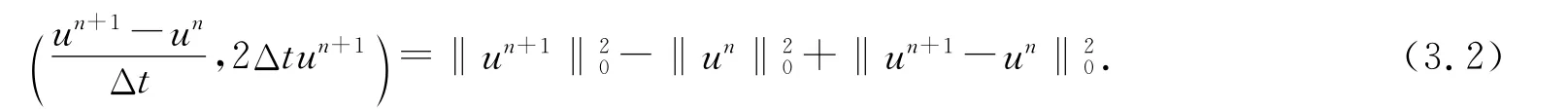
直接计算即可得此结论.

由上述两个引理可以得到离散格式的稳定性结果.

定理3.1 时间半离散格式（3.1）是条件稳定的，即当Δt≤2ν时，

证明 由方程（3.1）与2Δtun＋1做内积可得

定理得证.

BD2格式 考虑基于Adam－Basshorth方法的二阶半隐格式

对第一步进行考察

引理3.3 对所有网格函数｛ un｝ ，有

证明 令

那么

引理得证.

引理3.4 对所有网格函数｛ un｝ ，有（2∂xun＋1（2un－un－1）＋un＋1∂x（2un－un－1），un＋1）＝0.

证明

引理得证.

同理我们可以得到二阶BD2离散格式的稳定性结果.

定理3.2 BD2格式，即方程（3.3）是条件稳定的，亦即当Δt≤ν时，有

证明 方程（3.3）与4Δtun＋1做内积可得

丢掉一些正项，我们有

定理得证.

C－N 格式 考虑基于Crank－Nicolson方法的二阶半隐格式

这里

引理3.5 对所有网格函数｛ un｝ ，有

证明

引理得证.

同理我们可以得到二阶C－N 离散格式的稳定性结果.

定理3.3 半离散C－N 格式是条件稳定的，即当Δt≤4ν时，

因此

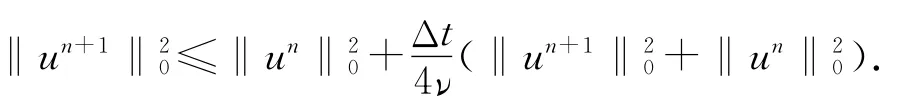
定理得证.

其他高阶半隐式格式

三阶半隐格式

四阶半隐格式

五阶半隐格式

六阶半隐格式

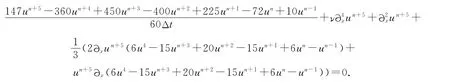
4 数值结果

4.1 数值结果的有效性

这里，我们讨论一些计算的细节，并讨论数值解的有效性.定义

Euler／F格式

BD2／F格式

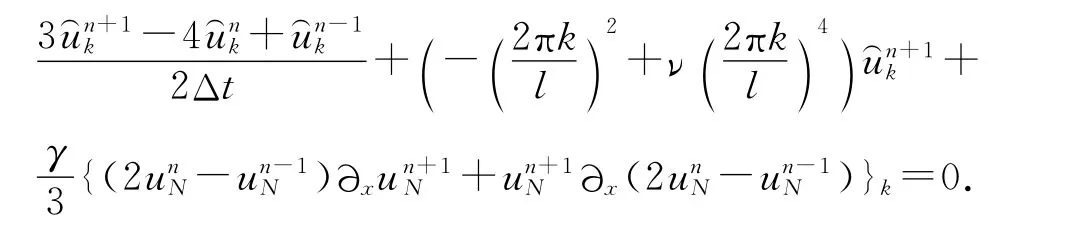
C－N／F格式

事实上，找到方程（2.1）—（2.3）的准确解是异常困难的，为了验证数值格式的有效性，定义收敛阶

固定初值u0（x）＝cosx（1＋sinx），T＝1，l＝2π，N＝128.我们测试了不同的ν，Δt对收敛阶的影响，计算结果如表1—3.从表中可知Euler／F格式在时间方向上有一阶精度，BD2／F和C－N／F格式在时间方向上有二阶精度，这表明我们的数值格式是有效的.当ν＝0时，计算格式是失效的，因为此时方程可能是病态的.

表1 Euler／F格式收敛阶随Δt与ν 的变化情况

表2 BD2／F格式收敛阶随Δt与ν 的变化情况

表3 C－N／F格式收敛阶随Δt与ν 的变化情况

4.2 混沌行为

受J.Hyman，A.Aceves等人工作的启发［1－2，5－6，10，16］，这里将用BD2／F格式考察K－S方程解的混沌和周期性质，我们固定取不同的初值，解随时间的变化情况如图1—2所示，我们可以很清晰地看到解的混沌和周期性质.值得一提的是，图1与文献［10］中解的结构（14页，图4－1）是一致的.这为文献［16］讨论的偏微分方程混沌现象提供了具体的例子.

最后，用BD2／F格式测试参数ν对数值解的影响.在图3—6中，取l＝2π.可以看到解的结构对ν的变化是非常敏感的，解的周期运动与非周期运动相互纠缠，并且表现出很复杂的混沌性质，当ν≥0.25时数值解是平凡解.

图3 ν＝0.01，ν＝0.012时解的结构

图4 ν＝0.015，ν＝0.024时解的结构

图5 ν＝0.04，ν＝0.045时解的结构

图6 ν＝0.06，ν＝0.25时解的结构

5 结论

讨论了K－S方程的数值方法，提出了一系列的半隐格式，其优点在于每步迭代只需要解一个线性方程.我们用新提出的方法考察了K－S方程解的性质，得到了一些解的混沌性质.

［1］HYMAN J，NICOLAENKO B.The Kuramoto－Sivashinsky equation：a bridge between PDE's and dynamical systems［J］.Physica D：Nonlinear Phenomena，1986，18（1）：113－126.

［2］HYMAN J，NICOLAENKO B，ZALESKI S.Order and complexity in the Kuramoto－Sivashinsky model of weakly turbulent interfaces［J］.Physica D：Nonlinear Phenomena，1986，23（1）：265－292.

［3］KEVREKIDIS I，NICOLAENKO B，SCOVEL J.Back in the saddle again：a computer assisted study of the Kuramoto－Sivashinsky equation［J］.SIAM Journal on Applied Mathematics，1990，50（3）：760－790.

［4］JOLLY M，KEVREKIDIS I，TITI E.Approximate inertial manifolds for the Kuramoto－Sivashinsky equation：analysis and computations［J］.Physica D：Nonlinear Phenomena，1990，44（1）：38－60.

［5］SMYRLIS Y，PAPAGEORGIOU DT.Predicting chaos for infinite dimensional dynamical systems：The Kuramoto－Sivashinsky equation，a case study［J］.Proceedings of the National Academy of Sciences，1991，88（24）：11129－11132.

［6］PAPAGEORGIOU D，SMYRLIS Y.Computer assisted study of strange attractors of the Kuramoto－Sivashinsky equation［J］.Zeitschrift fur angewandte Mathematik und Mechanik，1996，76：57－60.

［7］CUETO FELGUEROSO L，PERAIRE J.A time－adaptive finite volume method for the Cahn－Hilliard and Kuramoto－Sivashinsky equations［J］.Journal of Computational Physics，2008，227（24）：9985－10017.

［8］PAPAGEORGIOU D T，SMYRLIS Y S.The route to chaos for the Kuramoto－Sivashinsky equation［J］.Theoretical and Computational Fluid Dynamics，1991，3（1）：15－42.

［9］LOPEZ－MARCOS M.Numerical analysis of pseudospectral methods for the Kuramoto－Sivashinsky equation［J］.IMA Journal of Numerical Analysis，1994，14（2）：233－242.

［10］KASSAM A，TREFETHEN L N.Fourth－order time－stepping for stiff PDEs［J］.SIAM Journal on Scientific Computing，2005，26（4）：1214－1233.

［11］AKRIVIS D.Finite difference discretization of the Kuramoto－Sivashinsky equation［J］.Numerische Mathematik，1992，63（1）：1－11.

［12］AKRIVIS G，CROUZEIX M，MAKRIDAKIS C.Implicit－explicit multistep finite element methods for nonlinear parabolic problems［J］.Mathematics of Computation of the American Mathematical Society，1998，67（222）：457－477.

［13］GEORGIOS AKRIVIS，MICHEL CROUZEIX，CHARALAMBOS MAKRIDAKIS.Implicit－explicit multistep methods for quasilinear parabolic equations［J］.Numerische Mathematik，1999，82（4）：521－541.

［14］AKRIVIS G，SMYRLIS Y S.Implicit－explicit BDF methods for the Kuramoto－Sivashinsky equation［J］.Applied Numerical Mathematics，2004，51（2）：151－169.

［15］KHATER A，TEMSAH R.Numerical solutions of the generalized Kuramoto－Sivashinsky equation by Chebyshev spectral collocation methods［J］.Computers ＆ Mathematics with Applications，2008，56（6）：1465－1472.

［16］ACEVES A，ADACHIHARA H，JONES C，et al.Chaos and coherent structures in partial differential equations［J］.Physica D：Nonlinear Phenomena，1986，18（1）：85－112.