边界增长网络模型的演化性质

刘 霞，姚东任，姚 兵

（1.西北师范大学数学与统计学院，甘肃 兰州730070；2.西北师范大学计算机科学与工程学院，甘肃 兰州730070）

1 预备知识

关于复杂网络动力学研究是当今网络研究中的关键课题.1959年，P.Erdös和A.Rényi首先研究了在随机网络中最大和最小度的分布［1］，Bollobás（1981）随后得到了所有度分布的形式.D.J.Watts和S.H.Strogatz在1998年结合规则网络和随机网络的特点给出了（WS）小世界网络的生成机制模型［2］.小世界网络是在规则网络的基础上加入随机性产生的，即对规则网络的每一个节点的所有边（节点之间的连线），以概率p 断开一个端节点，并重新连接，连接的新端节点从网络中的其他节点里随机选择，如果选择的节点已经与此节点相连，则再随机的选择其他节点来重新连线.在复杂网络的研究中，网络如果同时具有大聚集程度和小最短路径这两个性质，就说它具有小世界效应.1999年，美国的物理学家A.L.Barabási和他的博士生R.Albert进行万维网的研究时，发现通过超链接与网页、文件所构成的万维网网络并不是如一般的随机网络一样，有着均匀的度分布［3］.他们发现万维网是由少数高连接性的页面串联起来的.绝大多数（超过80%）的网页只有不超过4个超链接，但极少数页面（不到总页面数的1／10 000）却拥有超过1 000个的链接，个别文件甚至与超过200万个其他页面相连.所谓的无标度，是指虽然网络中大部分节点的度不高，但极少数节点的度不受任何限制，可以变得十分巨大.幂率度分布使网络在小世界特有的基础上又具备了许多新的性质.网络的大部分节点度值都很低，但存在着度值非常高的中枢节点，这种关键的节点的存在使得无尺度网络对意外故障有强大的承受能力，但面对协同性攻击时则显得脆弱.现实中的许多网络都带有无标度的特性.例如，社会人际网络，信息交换网（万维网、国际互联网、电话网），社会网络（金融系统网络、科研合作网、交通网），生物网络（细胞网络、生态网络）等等.

已知很多动态网络（dynamic network）可以表示成N（t）＝（P（u，k，t），G（t），UG），t∈［a，b］.其中P（u，k，t）是一个节点u和k 个节点连接的概率，G（t）是N（t）的连通拓扑结构，UG 是N（t）在时间区间［a，b］上的底图［4］.当概率P（u，k，t）服从幂率分布k－α，2＜α＜3，则称G（t）为无标度图，G（a）为初始化图，N（t）为无标度网络（scale－free network）［5－9］.当前，利用图论的理论和技术来研究动态网络成为一个有效且有力的手段.为动态网络建立数学模型，或者建立数学模型来模拟实际网络已经成为不可缺少的技术环节［9－10］.受文献［9］的研究技术启发，本文构造了一种新的边界增长网络模型，并对这类网络模型的主要特性进行研究，进而证明了这类网络模型的无标度性.为探索网络无标度性的必要条件，设计了新的统计指标：边累积分布，节点数目比和边数目比，并将此在本文的边界增长网络模型中加以应用.

2 边界增长网络模型

2.1 基本参数

对任意给定的至少有2个节点的连通网络N（0），用记号nv（0）和ne（0）分别表示它的节点个数和边数目，记号V（0）和E（0）分别表示网络N（0）的节点集合和边集合，使得n0（0）＝｜V（0）｜，ne（0）＝｜E（0）｜.对于网络N（0）的每一条边uv∈E（0），新增加m 个节点，并且将这m 个节点与节点u，v 分别相连，产生t＝1时刻的网络N（1），并将最后一个新节点w 与节点u，v 分别相连所得的边wu 和边wv定义为网络N（1）的边界边（bound edge）.记号X1代表N（0）新增加节点的集合，Y1代表新增加的边集合，则有Y1＝｛wu，wv：uv∈E（0），w∈X1｝，以及V（1）＝V（0）∪X1，E（1）＝E（0）∪Y1，｜Y1｜＝2·｜X1｜＝2mne（0）.

类似地，对于网络N（1）的每条边界边xy∈E（1），新增加m 个新节点，并且将这m 个节点分别与节点x 和节点y 相连，从而得到t＝2时刻的网络N（2），并将最后一个新节点z与节点x，y 分别相连所得的边zx 和zy 定义为网络N（2）的边界边，显然有V（2）＝V（1）∪X2，E（2）＝E（1）∪Y2.依此类推，从网络N（t－1）可得到网络N（t）.以下称N（t）为边界增长网络模型（bound growing network model），简称为边界增长网络；称N（0）为初始网络（initial network）.见图1—2.下面给出边界增长网络N（t）的一些基本参数.对t≥1，边界增长网络N（t）的节点集合V（t）与边集合E（t）分别为：

其中：Xt表示t时刻新增节点的集合，Yt表示时间步骤t时新增边的集合.因为

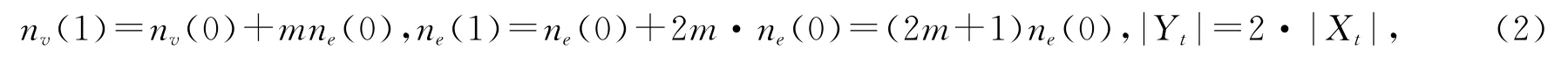
不难得到N（t）的节点数目和边数目分别如下：

边界增长网络N（k）的新增加节点数目

且有2kne（0）条边界边，最大度Δ（N（t））＝（tm＋1）·Δ（N（0）），最小度δ（N（t））＝2.此外，N（t）的平均度

平均度〈k〉说明边界增长网络N（t）是一个稀疏网络，也是树型网络.公式（3）表明N（t）具有优先链接性，即新进入N（t）的节点与初始网络中的节点相连线.同时，N（t）的构造表明N（t）具有增长性.故N（t）属于BA 无标度模型.

图1 当m＝3时，N（0）＝K3 和N（1）网络生成示意图

图2 当m＝3时，N（2）及N（3）网络生成示意图

2.2 度分布性质

下面将证明边界增长网络N（t）的无标度性与初始网络N（0）的结构无关（计算方法参见文献［9］）.

设d1，d2，…，da为初始网络N（0）的全体不相同的度，ndj（0）为具有度数dj的节点的个数.不妨设d1＞d2＞…＞da.则初始网络N（0）的度数为dj的节点在边界增长网络N（k）（k≥1）中的度数为2k－1m·dj，且记号k（i，N（t））表示t时刻节点i 的度数，P（k）表示随机选择恰好连接k条边的节点的概率，tc，i表示节点i被新增进网络的时刻.由于k（i，N（t＋1））＝k（i，N（t））＋2m，且k（i，N（tc，i））＝2.所以

注意到tc，i∈｛1，2，…，t｝，边界增长网络N（t）中度数d＝2，2＋2m，2＋4m，…，2＋2（t－1）m，2＋2tm，2t－1m·da，2t－1m·da－1，…，2t－1m·d1的 节 点 的 个 数通常，称上述边界增长网络N（t）的度数和节点个数的关系为N（t）的度谱（degree spectrum）.

边界增长网络N（t）的连接概率P（k）（connection probability）.

注意到N（t）的度谱属于离散型，下面计算边界增长网络N（t）的随机选择恰好有k 条边的节点的概率P（k）.根据（4）式，

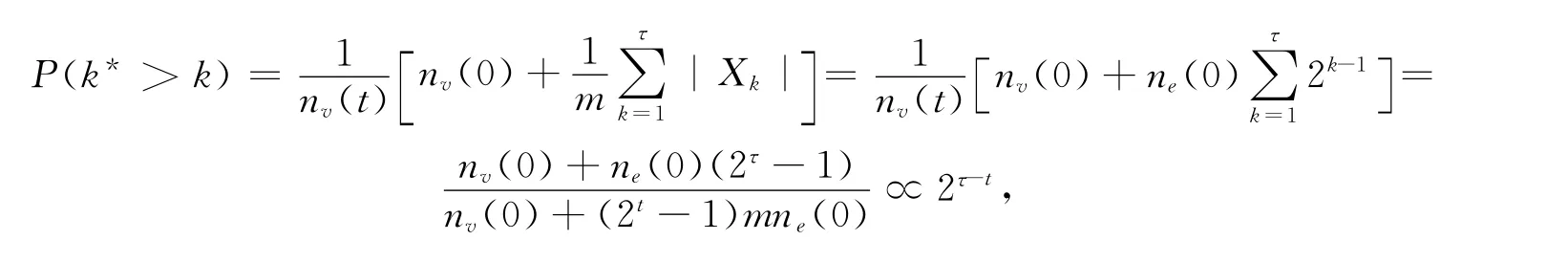
故边界增长网络N（t）服从指数分布，即是无标度网络.

2.3 聚类系数

对边界增长网络N（t）的节点i，记号Ei表示与节点i相邻的ki个节点间实际的边数表示ki个节点间最大的边数，那么节点i 的聚类系数是图G 的 聚 类 系 数〈c〉＝当新节点i加入边界增长网络N（t）时，它的度ki和Ei分别为2和1.当节点的度数每增加2m 时，Ei也增加2m，也就是说节点i的度ki随着时间增加时，它所对应的Ei增加相同的数目，而最开始时E1＝k1－1，也就是Ei始终比ki多1，即Ei＝ki－1.对于任意度为k的节点，聚类系数C〈k〉＝即C〈k〉～k－1.令kr＝2＋2（t－r）m 表示N（t）中标号为r的节点的度，可以算出度为kr的节点的聚类系数为再令Δnv（r）（0≤r≤t）表示度为kr的节点的数目（由上面的度谱可以得到），所谓求网络的聚类系数，也就是求它的所有节点的聚类系数的平均值，将度相同的节点的聚类系数与节点的数目相乘再相加，然后除以网络的节点数.所以，对任意t时刻，边界增长网络N（t）的聚类系数

可以估计

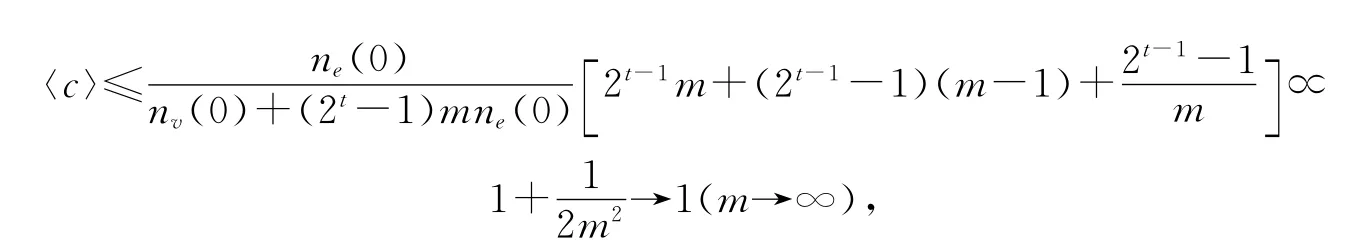
以及

那么，唯一的可能性是〈c〉→1（m→∞，t→∞），即边界增长网络N（t）具有高聚类性质.

3 其他统计指标

基于实际问题研究的需要，我们提出以下统计指标，期望能更好地研究增长型网络.

3.1 边累积分布

当τ＜t时，τ时刻N（τ）的节点i的度K（i，N（τ））之和记为∑K（i，N（τ））；时间步骤t时，N（t）的节点j的度K（j，N（t））之和记为∑K（j，N（t））.定义边界增长网络N（t）的边累积分布（edge－cumulative distribution）为

根据（3）式，当t较大时，

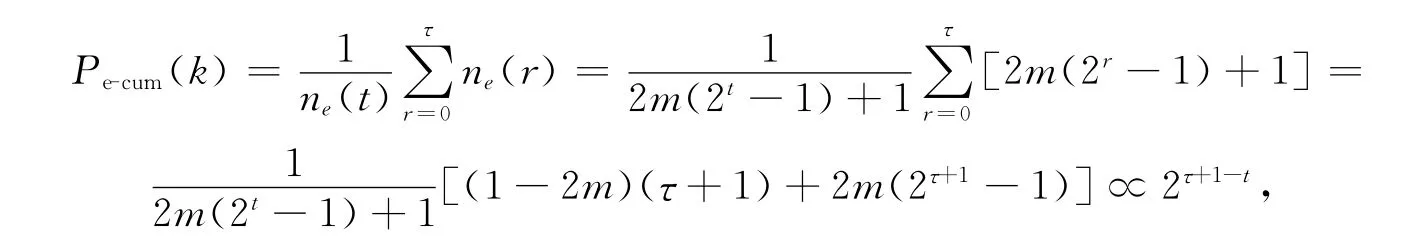
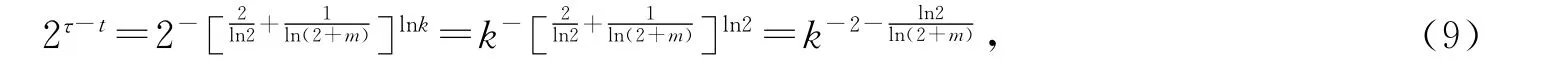
且

进而有

（10）式表明，边界增长网络N（t）的边累积分布Pe－cum（k）服从无标度分布.

3.2 （αk，βk）－增长网络模型

首先，计算边界增长网络N（t）中度数不大于k的节点总数

取k＝2（t－r）m，节点数目比（node－number proportion）为

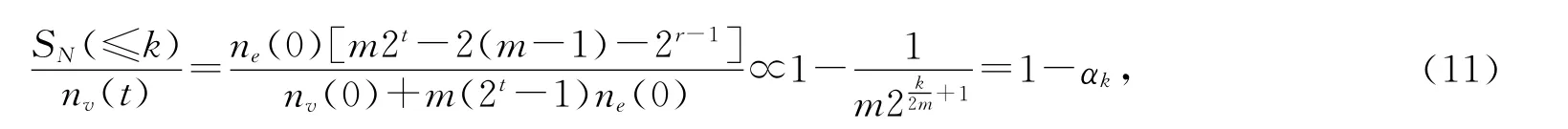
则当t很大时，有

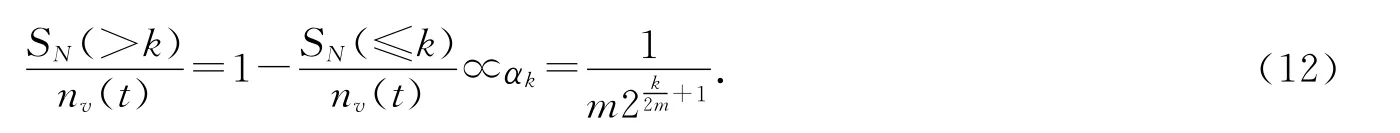
其次，计算边界增长网络N（t）中度数不大于k的节点的度数总和

令

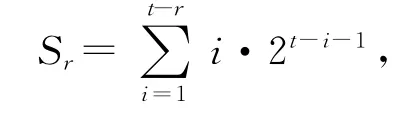
得

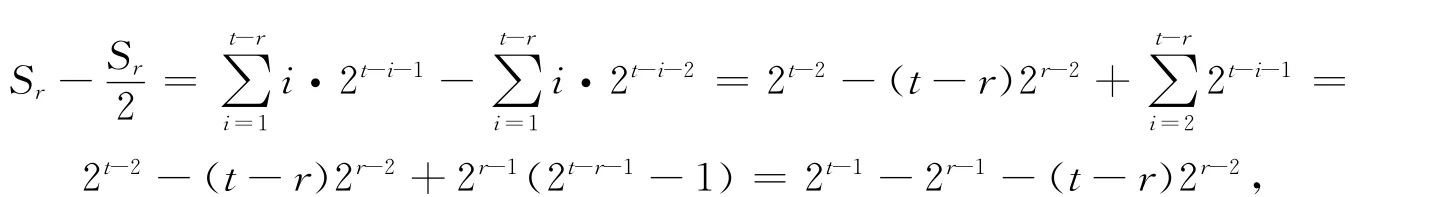
解得 取k＝2（t－r）m，计算边数目比（edge－number proportion）

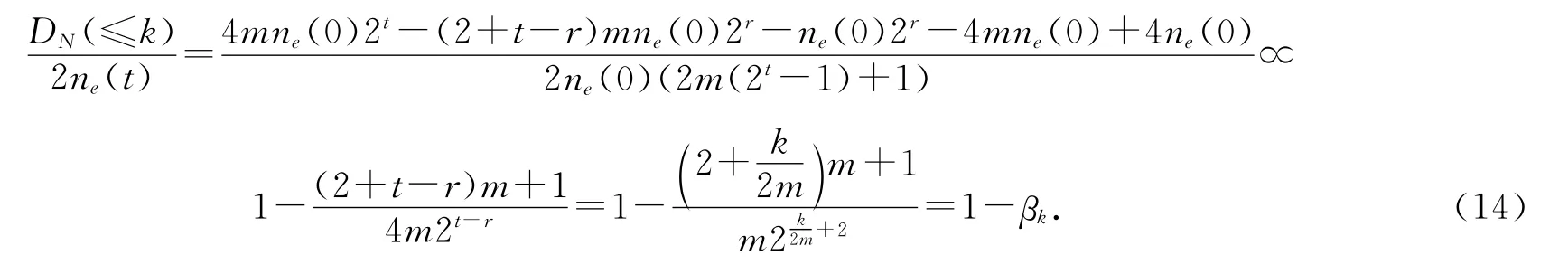
同理得

所以，边界增长网络N（t）可称为（αk，βk）－增长网络模型.

4 结论与问题

我们推广了文献［9］的增长型网络模型，得到并计算了新网络模型的幂律度分布、聚类系数等；提出了网络研究的新统计指标：边累积分布、节点数目比率与边数目和比率下的（αk，βk）－增长网络模型.显然，还需要对新的随机统计指标在其他的网络模型中进行广泛及深入地测试，修正其准确度、提高其精度.必须注意到，边界增长型网络N（t）在每一时刻t只有新进入网络的外部节点与N（t）内的节点可以连线，N（t）内的节点的度数和连线方式不再发生变化，即没有N（t）内的重新连线和添加新的连线.如果考虑边界增长型网络N（t）内的随机重新连线或者随机添加新的连线，所得到的模型对实际网络进行模拟则会更好些.

［1］ERDÖS P，RÉNYI A.On random graphs［J］.Publ Math Debrecen，1959（6）：290－297.

［2］WATTS D J，STROGATZ S H.Collective dynamics of‘small－world’networks［J］.Nature，1998，393：440－442.

［3］BARABÁSI A L，ALBERT R.Emergence of scaling in random networks［J］.Science，1999，286：509－512.

［4］YAO BING，YANG CHAO，YAO MING，et al.Graphs as models of scale－free networks［J］.Applied Mechanics and Materials，2013，380／384：2034－2037.

［5］BONDY J A，MURTY U S R.Graph theory with applications［M］.London：Macmillan，1976：35－41.

［6］KIM D H，NOH J D，JEONG H.Scale－free trees：the skeletons of complex networks［J］.Physical Review E，2004，70，04612：1－5.

［7］LI L，ALDERSON D，TANAKA R，et al.Towards a theory of scale－free graphs：definition，properties，and implications［J］.Internet Mathematics，2005，2（4）：431－523.

［8］YAO BING，ZHANG ZHONG－FU，WANG JIAN－FANG.Some results on spanning trees［J］.Acta Mathematicae Applicatae Sinica：English Series，2010，26（4）：607－616.

［9］ZHANG ZHONG－ZHI，RONG LI－LI，GUO CHONG－HUI.A deterministic small－world network created by edge iterations［J］.Physica A，2006，363：567－572.

［10］SAGY B，MIRA G，AVISHAI W.An incremental super－linear preferential Internet topology model［J］.LNCS，2004，3015：53－62.