Marcinkiewicz积分在加权Hardy空间的有界性

周淑娟

（青岛大学数学科学学院数学系，山东 青岛266071）

Hardy空间的理论是调和分析的主要内容.随着对Hardy空间的原子和分子刻画的研究，奇异积分算子在其上的有界性问题有了长足的发展.由于加权Hardy空间的原子和分子刻画的出现，使得对奇异积分算子在加权Hardy空间上有界性的讨论有了更简洁的方法［1－5］.

文献［6］定义了高维的Marcinkiewicz积分算子μΩ，并证明了若Ω 满足球面Sn－1上的Lipγ（0＜γ≤1）条件，那么算子μΩ 是弱（1，1）型和强（p，p）型的，1＜p＜2.文献［7］得到若Ω 在Sn－1上是连续可微的，则算子μΩ 是（p，p）型（1＜p＜∞）的结论.文献［8］证明了Ω∈H1（Sn－1）时，μΩ 在Lp（Rn）（1＜p＜∞）上有界.文献［9］则得到了Marcinkiewicz积分算子μΩ 是从H1（Rn）到L1（Rn）和从H1，∞（Rn）到L1，∞（Rn）有界的结论.文献［10］证明了Marcinkiewicz积分μΩ是（Hp，Lp）型和（Hp，∞，Lp，∞）型的算子（0＜p＜1）.文献［11］研究了Marcinkiewicz积分算子的加权有界性.

基于以上的研究，本文讨论了函数Ω∈Lipγ（Sn－1）时，Marcinkiewicz积分在加权Hardy空间的有界性问题，借助于权函数的性质及不等式估计，证明了Marcinkiewicz积分在加权Hardy空间上是有界的.

1 基本知识和理论

记Sn－1为Rn上的单位球面，其标准Lebesgue测度为dσ，设Ω 为Rn上的零次齐次函数，满足Ω∈L1（Sn－1），且

Marcinkiewicz积分算子μΩ 定义为

其中

称Ω 满足Lipγ（0＜γ≤1）条件，是指存在常数C＞0，对任意的x′，y′∈Sn－1有

Ap（1≤p＜∞）权函数的定义参见文献［12－13］用Lpω（Rn）表 示空 间Lp（Rn，ω（x）dx），且

定义1［1］设ω∈A∞（Rn），且0＜p≤1.加权Hardy空间Hpω（Rn）定义为Hpω（Rn）＝｛f∈S′（Rn）；其中φ∈S（Rn）为固定函数且t＞0.进一步定义‖f‖Hpω（Rn）＝‖φ＊（f）‖Lpω（Rn）.

定义2［1］设称Lqω（Rn）中的函数a（x）是一个ω－（p，q，s）原子，如果满足：

（1）supp a⊂Q，Q 是Rn上以x0为中心的方体；

（2）‖a‖Lqω（Rn）≤ω（Q）1／q－1／p；

定义3［3］设0＜p≤1≤q≤∞，p≠q，qω＝inf｛q≥1；ω∈Aq｝，rω≡｛r＞1：ω 满足r 阶反向Hölder不等式｝，s≥s0，ε＞max｛srω（rω－1）－1n－1＋（rω－1）－1，1／p－1｝，a1＝1－1／p＋ε，b＝1－1／q＋ε，s0＝称Lqω（Rn）中的函数M 是一个中心x0的ω－（p，q，s，ε）分子，如果满足：

加权Hardy空间的原子和分子分解如下：

引理1［1］令ω∈Aq，则每个ak（x）都是一个ω－（p，q，s）原子进一步其中下确界取遍f 的所有分解.

引理2［3］令ω∈Aq，则每个Mk（x）都是一个ω－（p，q，s，ε）原 子进一步其中下确界取遍f 的所有分解.

引理3［11］设1＜q＜∞，μΩ是Marcinkiewicz积分算子，则μΩ是Lq上的加权有界算子.

2 结论及其证明

本文的主要结果如下：

证明 只需证明，存在常数C＞0，使得对每一个ω－（p，2，s）原子a（x），μΩ 是一个中心ω －（p，2，s，ε）分子即可.由题设可知消失距条件成立，下面验证大小条件.

首先，由引理3，即μΩ的L2ω有界性，以及原子的大小条件知

对于另一部分，有

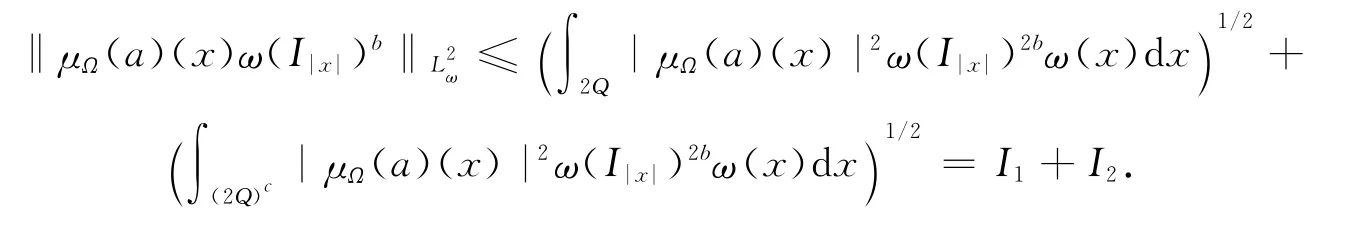
对于I1，同样由μΩ 的L2ω有界性及原子的大小条件得

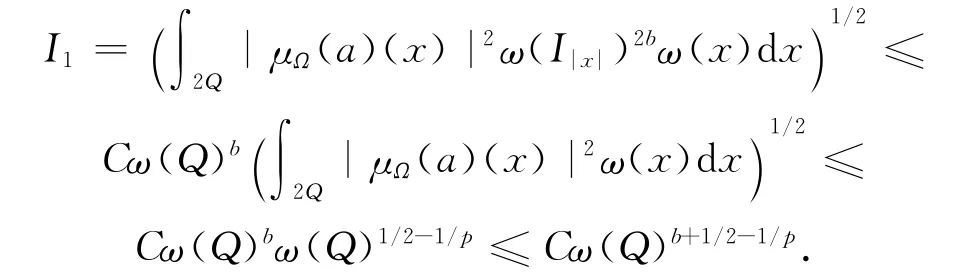
再估计I2.

对于I21，因 为 当x∈（2Q）c，y∈Q 时，有注意到当0＜γ≤1 时，Lipγ（Sn－1）⊂L∞（Sn－1），由Jensen不等式，以及a（y）的大小条件有

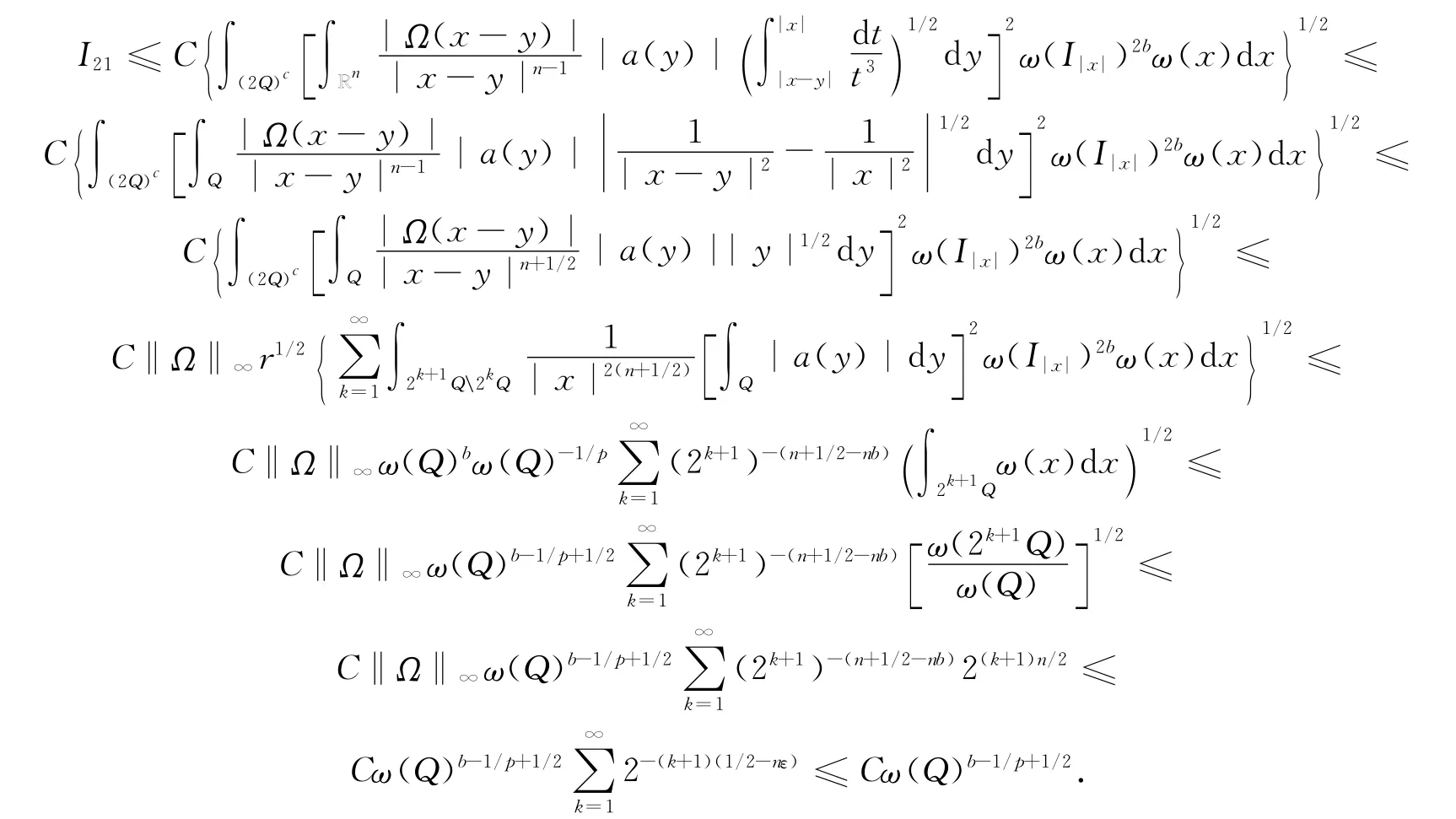
对于I22，因为Ω（x）满足Lipschitz条件，并且0＜γ≤1，所以有

从而，利用a（y）的消失距等条件，有

这就证明了

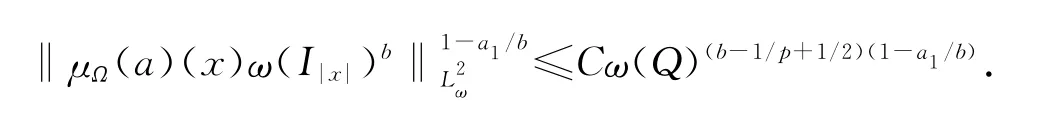
又因为

所以

定理得证.

［1］LI X M，PENG L Z.A weighted Hardy space and weighted norm inequalities for the area integral［J］.Acta Math Sinica：Chin Ser，1997，40：351－356.

［2］LI X M，PENG L Z.The molecular characterization of weighted Hardy spaces［J］.Sci China：Ser A，2001，44：201－211.

［3］LEE M Y，LIN C C.The molecular characterization of weighted Hardy spaces［J］.J Funct Anal，2002，188：442－460.

［4］QUEK TONGSENG，YANG DA－CHEN.Calderón－Zygmund－type operators on weighted weak Hardy spaces overRn［J］.Acta MathematicaSinica：English Series，2000，16（1）：141－160.

［5］赵凯，郝春燕，王磊.Marcinkiewicz积分在加权弱Hardy空间的有限性［J］.云南大学学报：自然科学版，2011，33（5）：502－506.

［6］STEIN E M.On the function of Littlewood－Paley，Lusin and Marcinkieicz［J］.Trans Amer Math Soc，1958，88：430－466.

［7］BENEDEK A，CALDERÓN A，PANZONE R.Convolution operators on Banach space valued functions［J］.Proc Nat Acad Sci USA，1962，48：356－365.

［8］DING YONG，FAN DA－SHAN，PAN YI－BIAO.Lp－boundedness of Marcinkewicz integral with Hardy space function kernel［J］.ActaMath Sinica：English Series，2000，16：593－600.

［9］DING YONG，LU SHAN－ZHEN，XUE QING－YING.Marcinkewicz integral on Hardy spaces［J］.Integr Equ Oper Theory，2002，42：174－182.

［10］丁勇，薛庆营.Hardy和弱Hardy上的Marcinkiewicz积分［J］.北京师范大学学报：自然科学版，2001，37（3）：292－298.

［11］TORCHINSKY A，WANG S.A note on the Marcinldewicz integral［J］.Colloquium Mathe－maticum，1990，60／61：235－243.

［12］GARCÍAS－CUERVA J，RUBIO DE FRANCIA J L.Weighted norm inequalities and related topics［M］.Amsterdam：North－Holland Math，1985：576－779.

［13］纪培胜，占小静，刘荣荣.Banach代数上双导子的Hyers－Ulam－Rassias稳定性［J］.东北师大学报：自然科学版，2013，45（4）：12－16.