共心双环势阱中自旋轨道耦合作用玻色爱因斯坦凝聚体的基态研究

陈光平

（四川文理学院物理与机电工程学院，四川达州635000）

共心双环势阱中自旋轨道耦合作用玻色爱因斯坦凝聚体的基态研究

陈光平

（四川文理学院物理与机电工程学院，四川达州635000）

研究了共心双环势阱中，自旋轨道耦合下的玻色爱因斯坦凝聚体的基态结构，发现随着自旋轨道耦合的变化，耦合系统呈现出丰富的基态结构。仅在一个方向加入自旋轨道耦合并随之增大时，系统基态密度呈现不均匀的角相分离分布，其相图显示它们仍然为驻波态；随着另一个垂直方向自旋轨道耦合强度的引入并逐渐增大到与原来方向相同，形成各向同性自旋轨道耦合时，系统基态密度逐渐形成均匀角相分离分布，从相位图中研究发现，各向同性自旋轨道耦合作用使系统基态产生了大量涡旋。

自旋轨道耦合；玻色⁃爱因斯坦凝聚；共心双环势阱；基态

0 引言

最近几年，人工合成Abelian规范势在实验中取得了巨大成功，引起了冷原子研究领域研究者的广泛兴趣[1⁃4]，他们开始考虑将其用于产生中性原子的自旋轨道耦合（SOC）并取得了较多的理论成果[5⁃8]；Wang等人发现玻色爱因斯坦凝聚体（BEC）的波函数呈现出非平凡结构；赝自旋为的两分量自旋轨道耦合玻色爱因斯坦凝聚体，随着相互作用强度的变化，基态波函数呈现出“平面波函数”和“驻波相”[9⁃10]。

研究者已经广泛研究了囚禁于简谐势阱中的SOC作用玻色爱因斯坦凝聚体[11⁃14]，Zhang等人详细研究了共心双环势阱中SOC作用玻色爱因斯坦凝聚体，包括无外势旋转[15]、有外势旋转[16]和赝自旋为1的三组分原子组成的玻色爱因斯坦凝聚体等[17]，他们研究发现引入自旋轨道耦合将大大丰富玻色爱因斯坦凝聚体的基态结构和产生丰富的相变。其中文献[15]研究发现引入自旋轨道耦合将增强原子间的相互作用，系统基态密度分布能够产生均匀的角向分离、径向相变和涡旋，相位图显示只要有自旋轨道耦合加入，系统就会产生涡旋。本文在此基础上，先研究只有一个方向有自旋轨道耦合并随之增加时，系统基态密度分布和相位分布情况，再研究固定一个方向自旋轨道耦合强度，在垂直于此方向上引入并加大自旋轨道耦合强度，各向异性自旋轨道耦合过渡到各向同性自旋轨道耦合的基态相变过程，通过研究以期发现各向异性自旋轨道耦合强度对BEC系统基态的影响。

1 理论模型

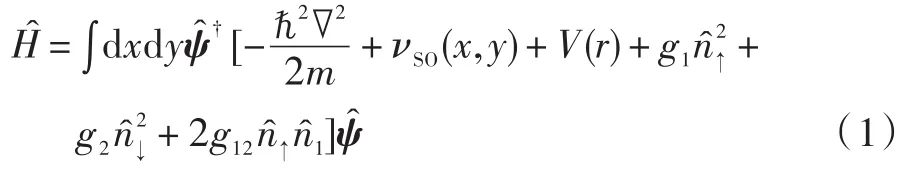
式中：V(z)为z方向（轴方向）的外势，为了简化计算，假设此方向约束极强而将系统外势近似为x⁃y平面内的二维约束势，可表达为：

采用平均场的方法做近似处理，经过推算得知Gross⁃Pitaevskii能量函数为：

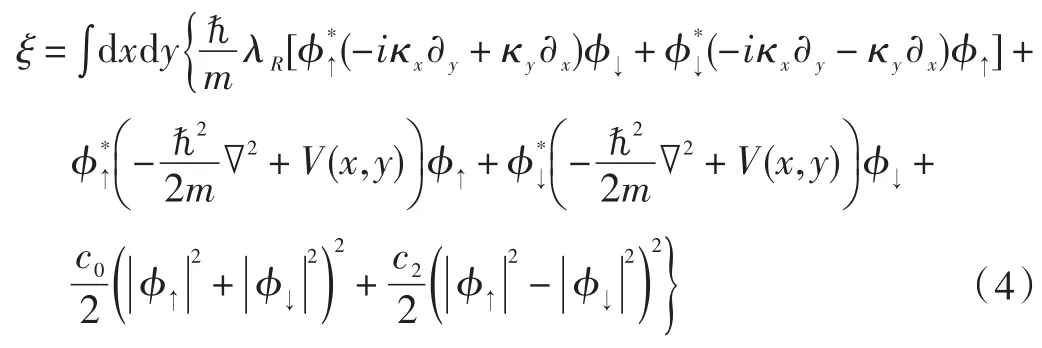
式中：c0=g+g12，c2=g-g12。为了研究系统参数对基态结构的影响，本文采用虚时演化和中心差分相结合的数值方法来求解SOC作用下的玻色爱因斯坦凝聚体的基态。

2 研究结果

在本文研究中，赝自旋向上和向下的原子初始波函数均取为高斯函数。引入自旋轨道耦合，将大大扩大系统调控参数空间的范围，为了简便起见，固定种内原子相互作用强度为g=g11=g12=15，和种间原子相互作用强度g12=g21=75，研究不同的自旋轨道耦合强度对系统基态的影响。

首先研究仅有y方向自旋轨道耦合，并且其强度逐渐增大时，凝聚体的基态密度和基态相的变化。图1为相互作用强度g=15,g12=75，x方向无自旋轨道耦合(κx=0)，y方向自旋轨道耦合强度κy=0,0.5,1.0,1.5,2.0（对应于图(a)～图(e)）时，赝自旋为-1/2的自旋轨道耦合凝聚体的基态密度相分布图。

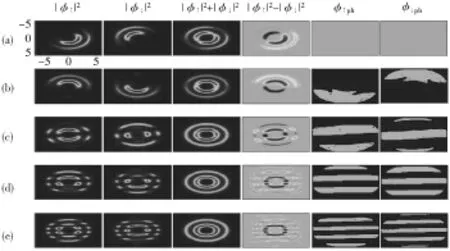
图1 赝自旋-1/2的自旋轨道耦合凝聚体的基态密度相分布图（一）

由图1（a）知，当系统没有自旋轨道耦合时，因系统参数g20区域，而自旋向下的原子堆积于y<0区域；两种原子的相位图中分别形成了上、下两块，呈现出较弱的驻波相分布。当κy=1.0时（见图1(c)），系统自旋向上和自旋向下的原子基态密度分布均开始出现角相分离，随着κy继续增大到1.5和2.0，系统基态密度分布角相分离更加明显，分离出的块状越来越多，但这些基态密度角向分离不均匀，与文献[15]提供的各向同性自旋轨道耦合作用BEC产生的基态密度均匀分布不同；再进一步观察原子基态相位图，惊奇地发现，这些角相分离在基态相密度分布图上呈现出块状分布，但是它的相位图却证实这些基态密度也仅仅是驻波相，理解为只有y方向自旋轨道耦合，并不能产生涡旋，只能产生条状驻波分布，但是由于双环势阱强力约束作用，这些条状基态密度被双环切成平行于x轴的块状分布。y方向自旋轨道耦合强度越大，条状驻波基态密度越细，被双环势阱切成点状越细越多，从图1（c）～图1（e）对比可以看出。

选取y方向自旋轨道耦合强度κy=2.0，x方向自旋轨道耦合强度从κx=0开始增加到κx=2.0，自旋轨道耦合逐渐从各向异性变换到各相同性。图2为相互作用强度g=15,g12=75，y方向自旋轨道耦合强度为κy=2.0，x方向自旋轨道耦合强度κx=0,0.5,1.0,1.5,2.0（对应于图2(a)～(e)）时，赝自旋-1/2的自旋轨道耦合凝聚体的基态密度相分布图。

图2 赝自旋-1/2的自旋轨道耦合凝聚体的基态密度相分布图（二）

图2（a）与图1（e）相同，此处不再赘述。由图2（b）可知，尽管x方向上加入了较小的自旋轨道耦合κx=0.5，这一强度不足以在基态密度分布上引起明显改变，但是从图2（b）第五、六两列相位图可以看出，在相位图上发生了明显的改变，相位显示基态不再是纯粹的驻波分布，而是呈现出一些涡旋分布。随着x方向自旋轨道耦合强度的增加，涡旋越来越明显；当κx=2.0时，自旋向上和向下原子的基态密度的块状分布在角向方向均匀分布，从图2（e）最后两列图，可知系统基态出现了均匀的涡旋结构。再来看径向方向基态密度的分布，因x方向自旋轨道耦合的引入并加强，原子间相互作用进一步得到增强，所以越来越多原子获得更多能量从内环跳至外环，因此，外环的原子越来越多，基态密度越来越大。

3 结论

本文采用虚时演化和中心差分数值法，研究了共心双环势阱中自旋轨道耦合玻色爱因斯坦凝聚体的基态结构问题，研究发现：只有一个方向有自旋轨道耦合时，共心双环势阱中凝聚体的基态密度呈现出不均匀的角相分离分布，其相位图显示其基态只是条状驻波态；不论这个方向上的自旋轨道耦合强度怎么增大，系统基态结构始终是驻波态不会产生涡旋态；只有在另一个方向引入自旋轨道耦合后，系统基态才可出现均匀的角相分离分布并产生逐渐均匀的涡旋态；随着均匀自旋轨道耦合的引入和加强，原子基态密度分布还将出现径向分离。

[1]GRISHKEVICH S，SAENZ A.Theoretical description of two ul⁃tracold atoms in a single site of a three⁃dimensional optical lat⁃tice using realistic interatomic interaction potentials[J].Physi⁃cal Review A，2009，80（1）：3403⁃3421.

[2]JUZELIUNAS G，RUSECKAS J.Non⁃abelian gauge potentials for ultracold atoms with degenerate dark states[J].Physical Re⁃view Letters，2005，95（1）：404⁃411.

[3]AICHHORN M，HOHENADLER M，TAHAN C，et al.Quan⁃tum fluctuations，temperature，and detuning effects in solid⁃light systems[J].Physical Review Letters，2008，100（21）：6401⁃6405.

[4]LIN Y J，COMPTON R L，PERRY A R，et al.Bose⁃Einstein condensate in a uniform light⁃induced vector potential[J].Physi⁃cal Review Letters，2009，102（13）：401⁃409.

[5]WANG Chun⁃ji，GAO Chao，JIAN Chao⁃ming，et al.Spin⁃or⁃bit coupled spinor Bose⁃Einstein condensates[J].Physical Re⁃view Letters，2010，105（16）：403⁃406.

[6]XU Xiao⁃qiang，HAN Jung⁃hoon.Spin⁃orbit coupled Bose⁃Ein⁃stein condensate under rotation[J].Physical Review Letters，2011，107（20）：401⁃411.

[7]LIN Y J，COMPTON R L，JIMENEZ G K，et al.Synthetic magnetic fields for ultracold neutral atoms[J].Nature，2009，462（81）：628⁃632.

[8]DIAZ B J，GUILLEUMAS M，LEWENSTEIN M，et al.Joseph⁃son oscillations in binary mixtures of F=1 spinor Bose⁃Einstein condensates[J].Physical Review A，80（23）：616⁃619.

[9]JI A C，LIU W M，SONG J L，et al.Dynamical creation of fractionalized vortices and vortex lattices[J].Physical Review Letters，2008，101（1）：402⁃407.

[10]ZHAI Hui.Spin⁃orbit coupled quantum gases[J].International Journal of Modern Physics B，2012，26（1）：723⁃728.

[11]HU H，RAMACHANDHRAN B，PU H，et al.Spin⁃orbit cou⁃pled weakly interacting Bose⁃Einstein condensates in harmonic traps[J].Physical Review Letters，2012，108（1）：402⁃406.

[12]SINHA S，NATH R，SANTOS L.Trapped two⁃dimensional condensates with synthetic spin⁃orbit coupling[J].Physical Review Letters，2011，107（27）：401⁃405.

[13]HU Hui，LIU Xia⁃ji.Critical temperature of a Rashba spin⁃or⁃bit⁃coupled Bose gas in a harmonic trap[J].Physical Review A，2012，85（1）：3619⁃3623.

[14]XU X Q，HAN J H.Spin⁃orbit coupled Bose⁃Einstein conden⁃sate under rotation[J].Physical Review Letters，2011，107（20）：401⁃403.

[15]ZHANG Xiao⁃fei，DONG Rui⁃fang，LIU Tao，et al.Spin⁃orbit⁃coupled Bose⁃Einstein condensates confined in concentrically coupled annular traps[J].Physical Review A，2012，86（6）：3628⁃3631.

[16]ZHANG Xiao⁃fei，GAO Ri⁃sheng，WANG Xin，et al.Bose⁃Einstein condensates in concentrically coupled annular traps with spin⁃orbit coupling and rotation[J].Physics Letter A，2013，377（16）：1109⁃1113.

[17]ZHANG Xiao⁃fei，LI Biao，ZHANG Shou⁃gang.Rotating spin⁃orbit coupled Bose⁃Einstein condensates in concentrically cou⁃pled annular traps[J].Laser Physics，2013，23（10）：5501⁃5504.

[18]陈光平.囚禁于简谐势+四次势阱中两组分旋转玻色爱因斯坦凝聚体[J].四川文理学院学报，2014（5）：30⁃33.

Ground state study of spin⁃orbit⁃coupled Bose⁃Einstein condensates in concentrical dual⁃ring potential well

CHEN Guang⁃ping
（School of Physics and Mech⁃Electronic Engineering，Sichuan University of Art and Science，Dazhou 635000，China）

The ground state structure of spin⁃orbit⁃coupled Bose⁃Einstein condensates in concentrical dual⁃ring potential well is studied，with changing of the spin⁃orbit⁃coupled，multiple ground state structures are appearing in the coupled system.If the spin⁃orbit⁃coupled is added increasingly only in one direction，inhomogeneous distribution of the azimuthal phase separation is appeared in the ground state density，however it is still the stating wave from the phase graph showing.The other spin⁃orbit⁃coupled strength is added increasingly in vertical direction until the same with the original direction，when the isotropy of spin⁃orbit⁃coupled is shaped，homogeneous distribution of the azimuthal phase separation is appeared gradually in the ground state density.Investigation from phase diagram shows that a large number of vortexes in ground state system are generated by the func⁃tion of isotropy spin⁃orbit⁃coupled.

spin⁃orbit⁃coupled；Bose⁃Einstein condensate；concentrical dual⁃ring potential well；ground state

TN201⁃34

A

1004⁃373X（2015）09⁃0135⁃03

陈光平（1981—），男，四川遂宁人，硕士，讲师。主要研究方向为复杂网络、冷原子。

2014⁃11⁃21

四川省科技厅应用基础重点资助项目（2011JY0063）；四川省教育厅成果培育项目（12ZZ021）；四川省教育厅重点项目（12ZA148；12ZB313）