基于反射对称性的极化SAR舰船目标CFAR检测

牛敏，王肖洋，高贵

（1.国防科学技术大学电子科学与工程学院，湖南长沙410073；2.电子信息系统复杂电磁环境效应国家重点实验室，河南洛阳471000）

基于反射对称性的极化SAR舰船目标CFAR检测

牛敏1，王肖洋2，高贵1

（1.国防科学技术大学电子科学与工程学院，湖南长沙410073；2.电子信息系统复杂电磁环境效应国家重点实验室，河南洛阳471000）

反射对称性是极化散射中十分重要的一种性质。反射对称性检测量刻画了共极化通道和交叉极化通道间的相关性，在极化合成孔径雷达（PolSAR）目标检测中有重要应用。在复Wishart分布的基础上，结合乘积模型，推导出反射对称性检测量统计模型服从K分布，利用实测数据证实该模型对杂波数据具有很好的拟合效果。最后基于K分布模型，用恒虚警率（CFAR）方法进行了舰船目标的检测，实验结果验证了该方法的有效性。

反射对称性；舰船目标检测；恒虚警率；极化合成孔径雷达

0 引言

合成孔径雷达（Synthetic Aperture Radar，SAR）具有独特的大范围、全天候、全天时的对地监视能力。利用SAR进行舰船目标检测，在海洋监视和海上救助方面具有十分关键的作用。随着极化SAR（Polarization Synthetic Aperture Radar，PolSAR）系统的快速发展，利用极化数据中丰富的极化信息进行舰船目标检测为SAR舰船目标检测开辟了新思路。

人造舰船和自然海洋表面具有不同的极化散射机理，基于这些极化散射差异有可能在极化SAR图像上把舰船目标从海洋中分离出来。Cameron于1996年提出了相干目标分解（Cameron Target Decomposition，CTD）理论[1]。1999年，Ringrose利用SIR⁃C的全极化数据，首次将Cameron分解方法应用于舰船目标检测[2]。2000年，加拿大的Touzi等利用极化熵方法对Convair⁃580的极化数据在不同入射角下进行了舰船检测研究[3]，实验结果证明入射角小于60°时，极化熵可增强目标与背景的对比度，但是不同的海况对该方法的影响较大。2001年，意大利学者Sciotti针对SIR⁃C全极化SAR数据提出了中心化法和非中心化法舰船检测方法[4]，该类方法检测效果较好，但运算时间较长。

1981年Van de首次提出了散射体及与其所对称的响应散射体的极化散射矩阵形式[5]。1992年S.V.Nghiem首次研究了极化SAR遥感的反射对称性问题[6]，2012年Nunziata与Migliaccio基于极化SAR数据中金属目标和海洋的反射对称性差异，首次利用极化协方差矩阵中的共极化（HH，VV）和交叉极化通道（HV）之间的相关性构建了一种新的检测量——反射对称检测量[7]，用于观测海洋中人造金属目标，该方法在理论上表现出较好的检测性能，利用反射对称性构造反射对称检测量进行舰船目标检测已经成为近几年极化SAR舰船目标检测的研究热点。然而在已有文献中该检测量在应用于目标检测时都是根据经验选取检测阈值，当SAR成像系统、海洋背景等条件发生变化时经验阈值往往发生变化，不具有很好的适应性，造成了基于反射对称检测量的检测方法在实际应用中困难重重，迫切需要研究相应的自适应检测方法。这其中，恒虚警率（Constant False Alarm Rate，CFAR）检测是雷达目标检测领域的经典和常用方法，具有广泛的应用前景，其首要和关键问题是研究相应检测量的杂波统计模型。但遗憾的是目前还没有文献给出基于极化协方差矩阵的反射对称性检测量的杂波统计模型，这也制约了CFAR检测在基于反射对称性舰船目标检测中的应用。

本文基于多变量复高斯统计分布理论，从复Wishart分布出发，结合乘积模型推导了反射对称检测量的统计分布，并采用对数累计量方法给出了参数估计方法，实测数据实验表明推导的理论分布能较好地拟合检测量分布直方图。最后采用CFAR检测，在不同的数据源、不同虚警率下对反射对称性检测和极化交叉熵检测的性能进行了对比，实验证明反射对称性检测量具有更优良的检测性能。

1 基于极化协方差矩阵的反射对称性检测量

在实际的遥感应用中，不存在完全的确定性散射体，因此为了处理统计散射效应和分析局部散射体，通常引入极化协方差矩阵，它由lexicographic基散射矢量导出，描述了散射体的不确定性散射过程[8⁃9]。利用lexicographic基表示的散射矢量直接包含了散射矩阵的复幅度信息，与系统的测量值直接对应，能够很好地解释物理散射机制。海面舰船目标由于其金属属性与海杂波之间的幅度对比度十分强，因此对海面目标进行极化检测可以强调利用幅度信息。因此，文献[5，10]在进行极化舰船检测时均是从极化协方差矩阵出发构造反射对称性检测量。

极化协方差矩阵表达形式如下：

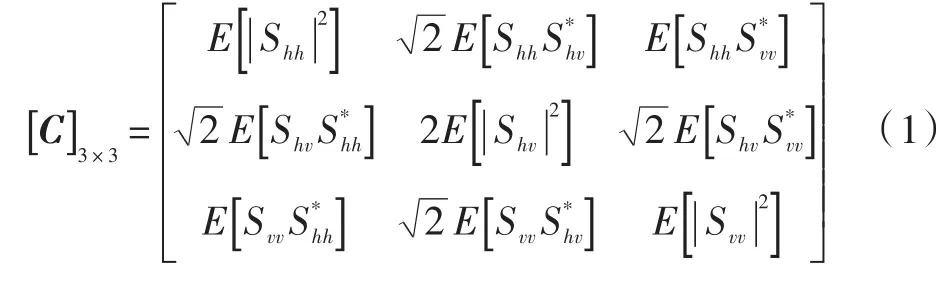
式中：E[·]表示随机散射介质各向同性下的空间统计平均；|·|和∗分别代表模和复共轭。

当极化SAR图像满足反射对称性条件时，S.V.Ng⁃hiem等人得出了一个重要的结论[5⁃6]，即极化协方差矩阵中的共极化和交叉极化通道之间的相关性消失，对应的散射系数为0，即，并构造了极化舰船目标反射对称性检测量：

表示共极化通道与交叉极化通道之间相关性的模。海平面满足反射对称性，所以R趋于0。舰船目标不满足对称反射性，所以R值较自由海面情况下会明显大于0。理论上，反射对称检测量同样可以构造为，但是研究表明，舰船目标在HH和HV极化通道中较为明显，而尾迹等海洋特征则在VV通道中较为明显，因此文中只对的统计分布进行研究[11⁃13]。

2 基于极化协方差矩阵的反射对称性检测量的统计建模

要获得式（2）的检测量的统计分布，首先要重新构造散射向量：

向量u的采样协方差矩阵可以表示如下：

令A=nZ，则有矩阵A服从复Wishart分布[14]：

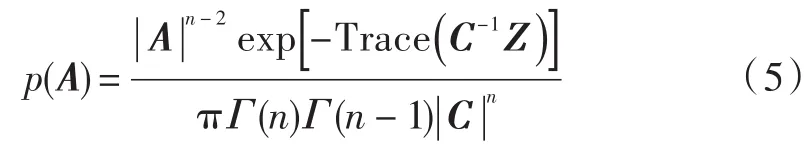
式中Γ(·)表示Gamma函数。

为了便于推导检测量R的统计分布，可以将式（4）给出的检测量进行归一化，归一化后的反射对称检测量可以表示如下：

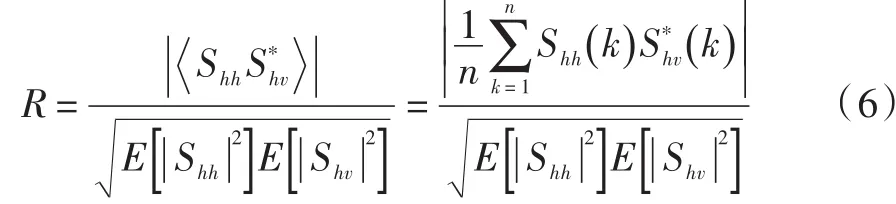
根据文献[15]可知，归一化检测量R的分布可从Wishart分布出发推导而来，有以下表达形式：

乘积模型是SAR图像建模中的常用模型，对复杂纹理的SAR图像有很好的建模能力[18]，其理论模型表示如下：

式中：I表示图像测量值；X表示地物纹理模型；Y为斑点噪声分量。

对于海面区域而言，海面不断起伏，长波之上伴随有许多短波毛刺，可以引入乘积模型来更好地描述海面SAR数据的起伏。引入乘性纹理分量后，归一化检测量R可重新表示为：

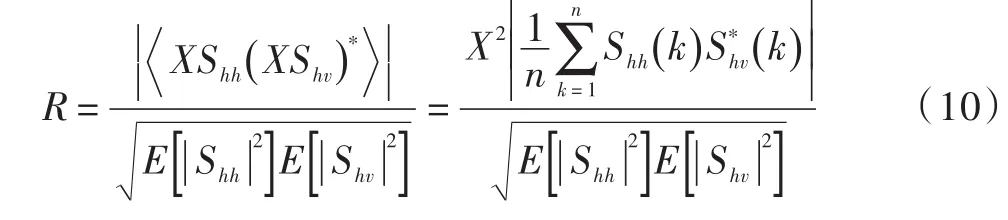
式中：α表示形状参数，与被测区域均匀度有关；λ表示尺度参数。

以乘积模型作为前提，以均匀区域下的扩展Gamma分布作为基础，结合方根Gamma分布，归一化检测量R服从如下分布：

在求得相关系数ρ之后，参数α0可以认为是常数，将α0λ看成一个整体，γ=α0λ，则式（13）即是常见的K分布：

设定理论虚警率Pfa计算检测门限T：

3 参数估计

K分布的参数估计方法常见的有最大似然估计（Maximum Likelihood，ML）、矩估计。ML估计方法是最优估计方法，但是通过对数似然函数很难得到形状参数和尺度参数。广泛采用的是基于矩估计的K分布参数估计法，其特点是形式简单、估计方便，但是该方法却存在诸多不足，突出表现为要单独估计有效视数n，而有效视数n的精度极大地影响了后续形状参数和尺度参数的估计精度，甚至使K分布失效。

文献[19]给出了一种对数累计量参数估计方法，该方法把有效视数n，同形状参数α、尺度参数γ一样视为待估计参数。而且基于对数累计量的参数估计方法，相当于对SAR图像数据做了对数变换后进行参数估计，有效缩小了低阶样本对数累计量的变化范围，也就是说不论杂波均匀度如何，都不会出现K分布失效的问题。因此本文也采用对数累计量方法进行K分布参数估计。

根据对数累计量方法得到的K分布参数估计表达式如下：

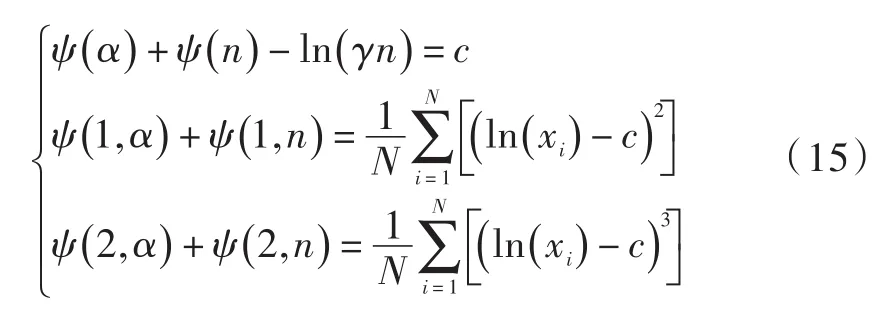
4 基于反射对称性的舰船目标CFAR检测流程

检测流程主要分为三步：

（2）估计分布参数，建立精准的理论统计模型；

（3）执行CFAR检测输出二值化检测结果图。

检测流程如图1所示。

图1 检测流程图

5 实验结果及分析

实验采用同一SAR平台，不同地区、不同分辨率、不同波段、不同海况下的极化数据充分验证K分布对反射对称检测量直方图的良好拟合性能以及反射对称检测方法的有效性。数据来源为美国NASA的AIR⁃SAR极化数据，日本东京湾极化数据和我国台湾高雄地区极化数据，数据示意图（Pauli基合成图）如图2所示。东京湾海域C波段水平极化（HH）数据如图2（a）所示，距离向和方位向理论分辨率为5 m×3 m，高雄港L波段水平极化数据如图2（b）所示，距离向和方位向理论分辨率为2.8 m×5 m。

图2 HH通道SAR示意图

5.1 检测量统计分布拟合

在水平极化（HH）、垂直极化（VV）和交叉极化（HV）通道数据中的相同位置割取一块海杂波切片，如图2中1号框标定区域所示，验证K分布对反射对称检测量直方图的拟合性能。首先按照式（8）对检测量进行归一化处理，并统计归一化后的检测量的直方图，然后根据文中第3节所提参数估计方法，对参数n，α，γ进行估计，拟合结果如图3所示。

图3 K分布对反射对称检测量直方图的拟合

东京湾区域和高雄港区域的参数γ，α，n的估计值分别如图3所示。拟合精度评价准则采用柯尔莫哥洛夫⁃斯摩洛夫（Kolmogorov⁃Smirnov，K⁃S）检验法，该检验方法利用观测数据的累积分布函数和已知模型分布函数FX(x)来计算两者幅度差值的上确界，即：

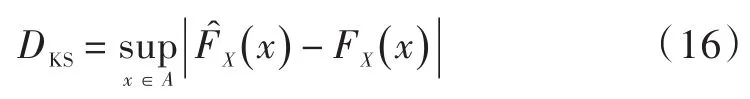
式中：A为观测数据的取值范围，统计量DKS值较小时，表明FX(x)和具有较好的匹配程度。

图3（a）和图3（b）对应的K⁃S检验统计量值的大小分别为0.090 9和0.150 3。观察图3，并分析K⁃S检验统计量DKS的大小可知，K分布对归一化后的反射对称检测量R具有良好的拟合效果。

5.2 舰船目标检测结果及检测性能分析

为了充分证明基于反射对称检测量的舰船目标CFAR检测的有效性，在实验中与文献[20]提出的极化交叉熵检测方法进行比较。极化熵描述了目标散射机理的随机变化，是极化目标分解理论中一种十分有效的目标检测方法。极化交叉熵方法是对极化熵的改进，基于目标和杂波相干矩阵的特征值分解提取识别特征，相比极化熵，能更进一步提高目标和杂波的对比度。

图2（a）中东京湾2号区域包含9个真实舰船目标，HH极化和HV极化数据示意图如图4（a）和图4（b）所示（图4中椭圆圈标定区域，通过多个极化通道幅度信息综合判读认为这些区域含有舰船目标）。图2（b）中高雄港2号区域包含24个真实舰船目标，HH极化和HV极化数据示意图如图4（c）和图4（d）所示。

图4 2号目标区域水平极化和交叉极化示意图

图5，图6给出了反射对称检测方法和极化交叉熵方法对东京湾和高雄港海域的检测结果。椭圆圈标定区域表示被成功检测的船只，箭头标定区域表示没有被检测到的船只（漏检），矩形框标定区域表示虚警。

从图5和图6的对比结果来看，在设定相同的理论虚警率下，反射对称性检测结果背景干净，目标完全被成功检测，整体检测结果显示虚警率很低（矩形框所标定），检测结果中目标结构信息保持较完整，充分反映了人造金属物体与海面的反射对称性差异。而极化交叉熵方法检测后目标部分丢失，如图6（c）和图6（d）所示，而且目标结构信息保持不完整，如图5（c）和图5（d）所示。

图5 东京湾海域检测结果对比

图6 高雄港海域检测结果对比

另外，在高海况下，极化交叉熵检测结果中虚警显著增多，整体检测性能下降明显；而反射对称性检测方法检测性能无明显变化，也说明了该方法对海况的变化有较好的适应性。分析其原因，极化交叉熵方法是假定目标和杂波有着不同的散射机理，反映了相邻分辨单元极化散射的随机性，因此目标和杂波之间的极化熵值可区分，但是如果杂波呈现非布拉格散射特性（高海况时），那么这个假设并不是完全成立的，这也正是为什么海况复杂后极化交叉熵检测结果明显下降的原因。相反，反射对称性方法和杂波、目标的后向散射机理无明显关系，主要反映了人造反射物体与自然反射物体在散射对称性上的区别。结果对比如表1所示。

表1 反射对称性和极化交叉熵检测结果对比

6 结语

本文基于极化SAR数据反射对称性原理，在复Wishart分布的基础上，结合乘积模型，推导出反射对称检测量服从K分布模型，并利用不同地区、不同波段的实测数据进行了实验验证。实验结果表明K分布能够很好地对实测区域的反射对称检测量进行拟合。同时，基于K分布的CFAR舰船检测结果表明，该检测方法相比文献[20]提出的极化交叉熵检测方法能够更好地实现对舰船目标的检测，且具有虚警率低的优点。

[1]CAMERON W L，YOUSSEF N N，LEUNG L L.Simulated po⁃larimetric signatures of primitive geometrical shapes[J].IEEE Transactions on Geoscience and Remote Sensing，1996，34（3）：793⁃803.

[2]RINGROSE R，HARRIS N.Ship detection using polarimetric SAR data[C]//Proceedings of Committee on Earth Observation Satellites.Toulouse：SAR Workshop，1999，450：687⁃691.

[3]TOUZI R，CHARBONNEAU F，HAWKINS R K，et al.Ship⁃sea contrast optimization when using polarimetric SARs[C]// IEEE 2001 International Conference on Geoscience and Re⁃mote Sensing Symposium.Sydney：IEEE，2001，1：426⁃428.

[4]SCIOTTI M，PASTINA D，LOMBARDO P.Polarimetric detec⁃tors of extended targets for ship detection in SAR images[C]// IEEE 2001 International Conference on Geoscience and Re⁃mote Sensing Symposium.Sydney：IEEE，2001，7：3132⁃3134.

[5]VAN DE HULST H C.Light scattering by small particles[M]. New York：John Willey&Sons，1981.

[6]NGHIEM S V，YUEH S H，KWOK R，et al.Symmetry proper⁃ties in polarimetric remote sensing[J].Radio Science，1992，27（5）：693⁃711.

[7]NUNZIATA F，MIGLIACCIO M，BROWN C E.Reflection symmetry for polarimetric observation of man⁃made metallic tar⁃gets at sea[J].IEEE Journal of Oceanic Engineering，2012，37（3）：384⁃394.

[8]王超，张红，陈曦，等.全极化合成孔径雷达图像处理[M].北京：科学出版社，2008.

[9]WANG Na，SHI Gong⁃tao，LIU Li，et al.Polarimetric SAR target detection using the reflection symmetry[J].IEEE Geoscience and Remote Sensing Letters，2012，9（6）：1104⁃1108.

[10]VELOTTO D，NUNZIATA F，MIGLIACCIO M，et al.Dual⁃polarimetric TerraSAR⁃X SAR data for target at sea observa⁃tion[J].IEEEGeoscienceandRemoteSensingLetters，2013，10（5）：1114⁃1118.

[11]BRUSCH S，LEHNER S，FRITZ T，et al.Ship surveillance with TerraSAR⁃X[J].IEEE Transactions on Geoscience and Remote Sensing，2011，49（3）：1092⁃1103.

[12]LIU C，VACHON P W，GELING G W.Improved ship detec⁃tion with airborne polarimetric SAR Data[J].Canadian Jour⁃nal of Remote Sensing，2005，31（1）：122⁃131.

[13]BECKETT K，THOMPSON A，LUSCOMBE A，et al.Optimi⁃zation of RADARSAT⁃2 SAR imagery for vessel detection ap⁃plications[C]//Remote Sensing of the Ocean，Sea Ice，and Large Water Regions.[S.l.]：SPIE 2010，7825：103⁃112.

[14]GOODMAN N R.Statistical analysis based on a certain multi⁃variate complex Gaussian distribution[J].Annals of Mathemati⁃cal Statistics，1963，34（1）：152⁃177.

[15]LEE J S，HOPPEL K W，MANGO S A，et al.Intensity and phase statistics of multi⁃look polarimetric and interferometric SAR imagery[J].IEEE Transactions on Geoscience and Re⁃mote Sensing，1994，32（5）：1017⁃1028.

[16]GRADSHTEYN I S，RYZHIK I M.Table of integrals，series，and products[M].San Diego：CA Academic Press，2007.

[17]时公涛，陈涛，陈东.干涉图幅度统计分布模型族及其参数估计[J].电子学报，2012，40（8）：1544⁃1551.

[18]WARD K D.Compound representation of high resolution sea clutter[J].Electronics Letters，1981，16（17）：561⁃563.

[19]时公涛，赵凌君，桂琳，等.基于Mellin变换的K分布参数估计新方法[J].电子学报，2010，38（9）：2083⁃2089.

[20]CHEN Jiong，CHEN Yi⁃lun，YANG Jian.Ship detection using polarization cross⁃entropy[J].IEEE Geoscience and Remote Sensing Letters，2009，6（4）：723⁃727.

Reflection symmetry based CFAR detection for polarization SAR ship targets

NIU Min1，WANG Xiao⁃yang2，GAO Gui1
（1.College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China；2.State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System，Luoyang 471000，China）

Reflection symmetry is a very importance property in polarization scattering.The correlation between the co⁃pola⁃rization channel and cross⁃polarization channel is described by reflection symmetry detection，it has important application in po⁃larization synthetic aperture radar（PolSAR）target detection.Based on complex Wishart distribution and combined with product model，it is inferred that the statistic model of the reflection symmetry detection quantity obeys K⁃distribution.The measured da⁃ta verified that good fitting effect of the clutter data is achieved by using the proposed model.Ship target detection is implemen⁃ted by the method of constant false alarm rate（CFAR）based on K⁃distribution model，and the experiment results verify the effi⁃ciency of the proposed detection.

reflection symmetry；ship target detection；CFAR；PolSAR

TN957.52⁃34

A

1004⁃373X（2015）09⁃0019⁃06

牛敏（1984—），男，内蒙古包头人，在读硕士研究生。研究方向为极化合成孔径雷达舰船目标检测。

王肖洋（1989—），男，河南漯河人，工学硕士。研究方向为合成孔径雷达地面运动目标检测、软件可重构雷达。

2014⁃12⁃26

高贵（1981—），男，内蒙古人，博士，副教授，硕士生导师，IEEE会员，在IEEE TGRS等国际期刊发表SCI论文22篇。研究领域涉及合成孔径雷达目标检测、模式识别、统计信号处理。