自选式网络调查的统计推断研究

刘 展

（中国人民大学 统计学院，北京 100872）

自选式网络调查的统计推断研究

刘 展

（中国人民大学 统计学院，北京 100872）

［摘 要］

自选式网络调查作为网络调查的形式之一，得到了越来越广泛的应用，但由于其入样概率未知，传统的概率抽样推断理论难以解决自选式网络调查的统计推断问题。为此，给出自选式网络调查总体均值、总量的估计及其性质，并对相应的性质进行推导证明，最后采用倾向得分的方法对估计进行加权调整，以修正之前的估计。

［关键词］

自选式网络调查；倾向得分；加权调整

一、引 言

随着网络的普及及其及时性、客观性、可靠性、低成本性和高效性等特点，越来越多的机构和组织开始采用网络调查。根据调查抽样的方式可将网络调查分为概率抽样的网络调查和非概率抽样的网络调查，非概率抽样的网络调查又可分为娱乐性网络调查、自选式网络调查和志愿固定样本的网络调查，本研究主要讨论自选式网络调查。自选式网络调查就是在各大门户网站上、网上讨论区或专门的调查网站公开发出邀请函，看到此函的上网者可自由选择是否参加调查，调查问卷只是简单地放在网上，回答者正好是上了网、访问了这个网址并决定去参与这个调查的人群；调查研究者并不控制选择的过程，选择概率是未知的，这样的调查称为自选式网络调查（Self-selected Web Survey）。自选式网络调查可能是当今网络调查中最为流行的形式，由于得到权威科研机构的支持而变得合法化。传统的抽样推断理论是基于概率抽样的基本原则从总体中随机抽取样本，总体中每一个单元都有一个非零的入样概率，而且所有的入样概率都是已知的，样本单元入样概率的倒数是其权数，将观测结果与样本单元的权数结合实现对总体目标量的估计。但是，自选式网络调查并没有样本的选择，整个总体可能就是一个样本，其样本从传统意义上讲是非概率的样本，入样概率未知，此时概率抽样的原则无法使用，那么如何实现自选式网络调查的统计推断就成为一个需要解决的问题。

纵观国内外关于网络调查的研究，已有一些研究者从不同的方面进行了探讨。国外的Grand-colas等采用了相同的问卷同时进行了网络和纸质的调查，并比较了回答者的均值、方差、偏度和峰度，发现许多显著的不同，同时采用卡方和回归模型去分析不同调查模式的效果，得出这些不同是由抽样偏差而非模式的不同所引起的。Bethlehem提出了自选式网络调查中总体均值估计的理论框架。Keusch建立了用于解释调查参与行为的理论框架与在线数据收集方法实证研究之间的系统联结，有助于研究者与实践者采用相应的技术提高网络调查的参与率。国内的刘昊探讨了网络调查中非抽样误差的来源，提出了预防非抽样误差的对策。马慧敏阐述了城镇住户网络调查中常见的几类非抽样误差，并对非抽样误差的控制提出了建议。樊茗癑与宗明刚在分析网络调查无回答问题的基础上，运用热卡插补法对网络调查无回答数据进行仿真控制，发现热卡插补法对网络调查无回答问题具有较好的事后补救效果。总之，国内外关于网络调查的研究主要集中在网络与纸质调查的比较、网络调查的参与与回答、非抽样误差等方面，而涉及自选式网络调查的研究非常少，关于自选式网络调查推断问题的研究就更为少见，且仅有的一些研究系统性不足。

本研究针对自选式网络调查进行系统性的探究，给出自选式网络调查总体均值、总量的估计及其性质，并对相应的性质进行推导证明，在此基础上进一步提出可采用倾向得分方法对估计进行加权调整，以提高估计的精度。

二、自选样本的估计

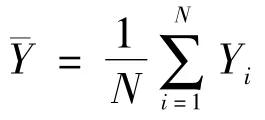
类似地，N＝N－N表示非网络总体U的规模，则N＋N＝N。非网络总体目标变量的均值定义为

为了便于讨论，现假定总体中的每个个体都能上网（U＝U），即目标总体就是网络总体。如果一个自选样本从网络中产生，参与一个自选式网络调查要求回答者能意识到调查的存在（他们必须是正好访问了这个网址或者看到了电子邮件信息，然后参与这项调查），并决定填网上的问卷，这就意味着在网络总体中的每一个单元i都有参与调查（回答）的未知概率p，i＝1，2，…，N。回答的单元可由一系列示性变量来表示，如R，R，…，R，其中第i个示性变量R是假定如果单元i回答（参与）则其值为1，否则其值为0，i＝1，2，…，N。R的期望值p＝E（R）称为单元i的回答概率，因此真正的样本量可表示为

（一）总体均值的估计

一般地，样本均值为

可用样本均值来估计总体均值。

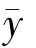
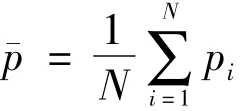
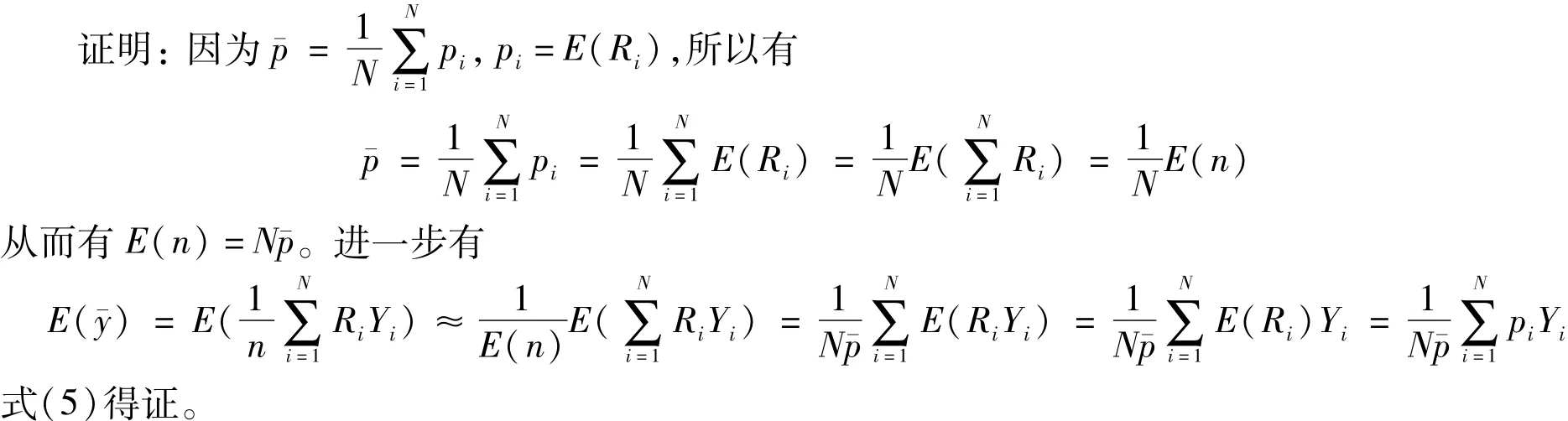
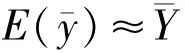
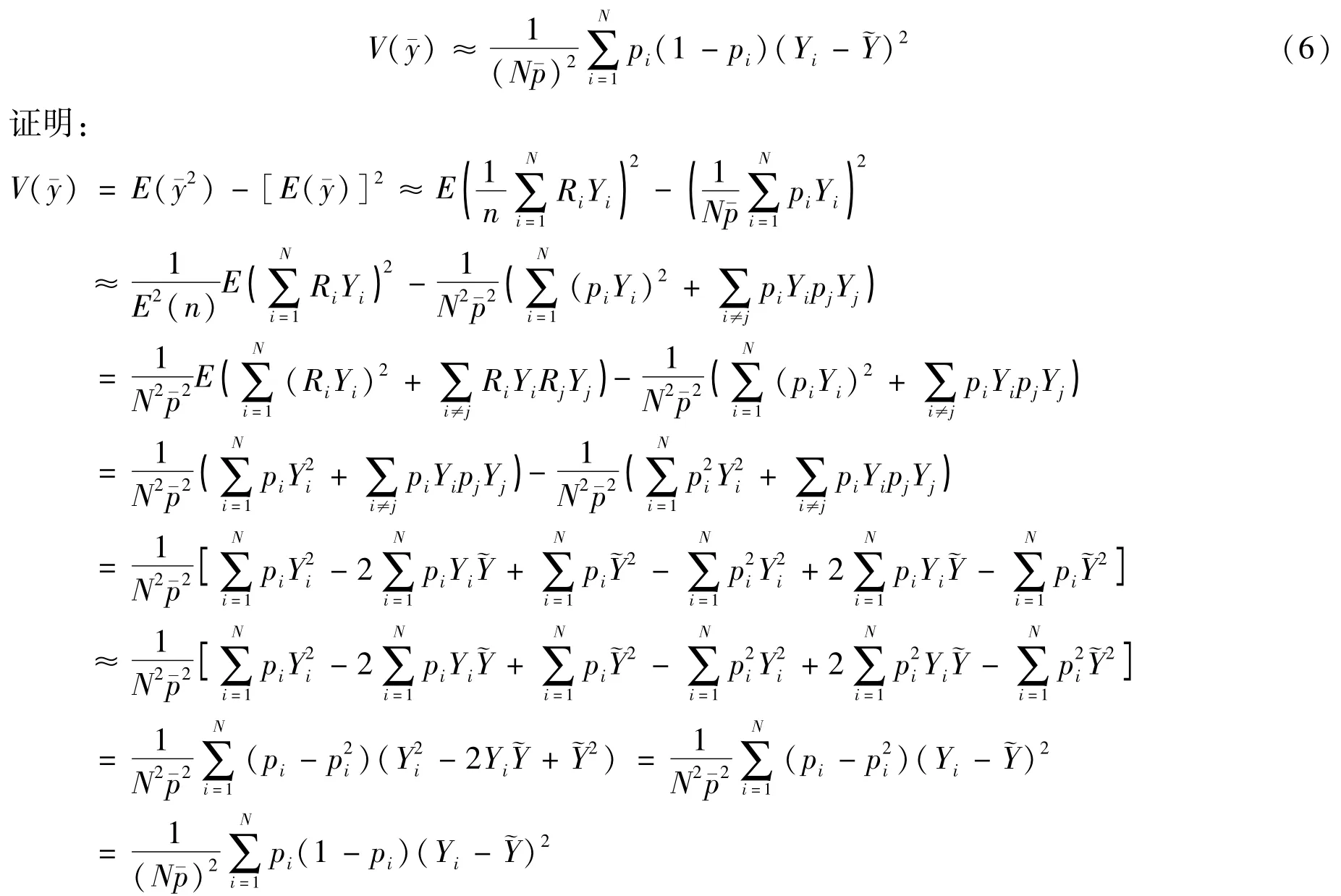
式（6）得证。

需要注意的是，方差的表达式并不包含样本量n（因为并没有确定的样本量），而是期望的样本量N珋p。因此，增加样本量并不会减少方差，即完成网上调查问卷的人增加也不会使方差减少。

性质3：珋y的偏差满足

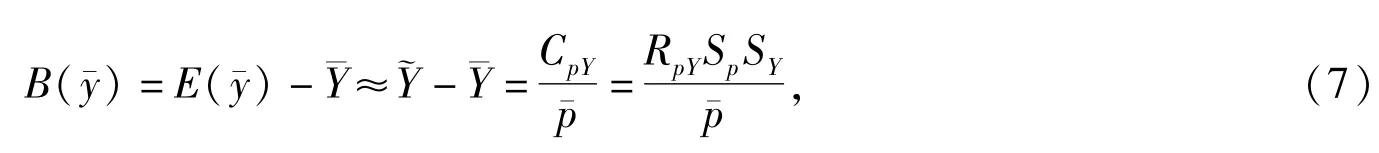
其中，

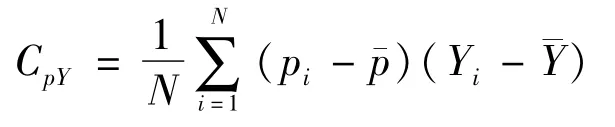
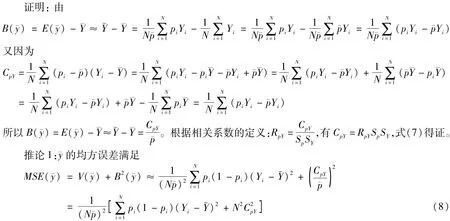
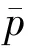
（二）总体总量的估计

当网络调查的目的是要估计总体总量时，则估计总体总量的公式比较简单，即在求均值的基础上乘以总体单元数N。总体总量的估计公式为：

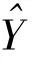
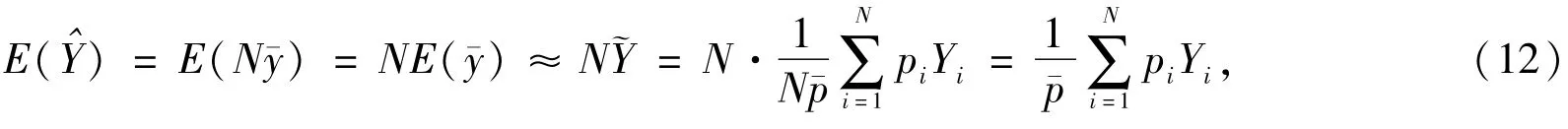
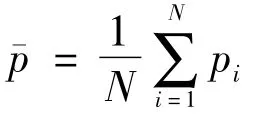
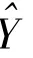
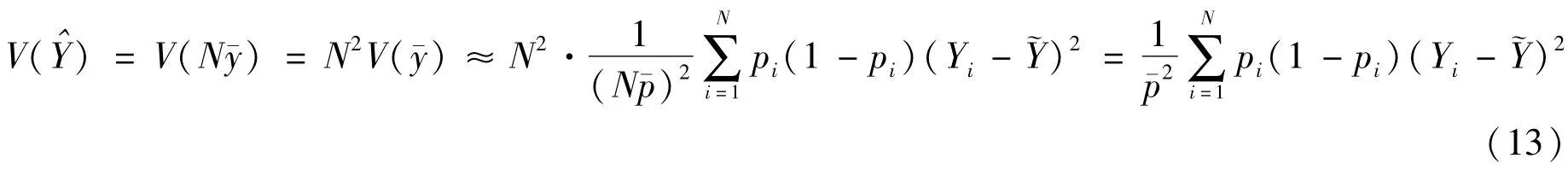
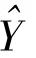
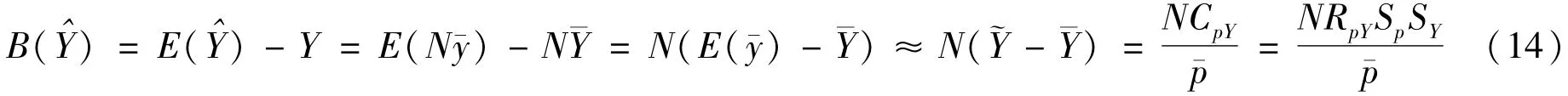
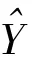
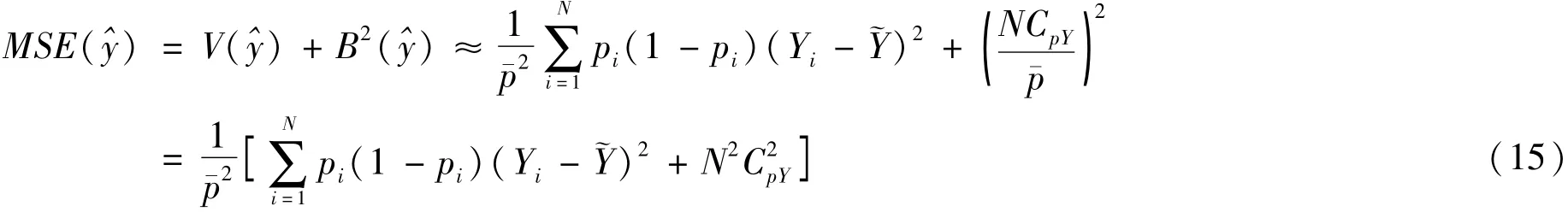
三、倾向得分加权调整

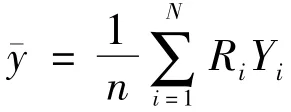
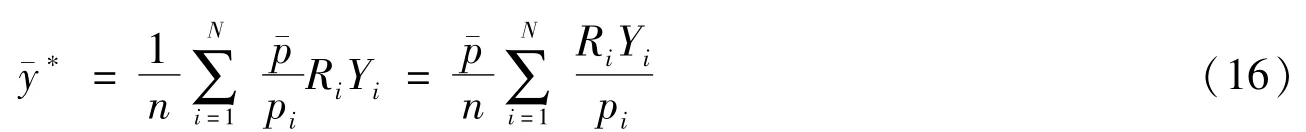
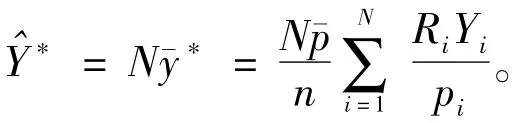
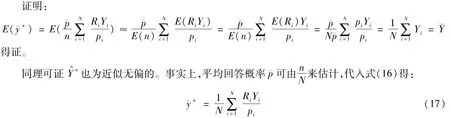
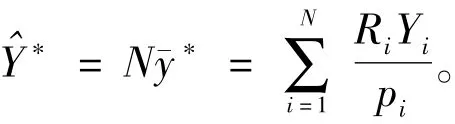
倾向得分方法是一种用于两个人群（总体）之间进行比较的统计方法，本质上，这种方法试图通过同时控制那些被认为比较有影响的全部变量的方式，来对两个人群之间的特征进行比较。在网络调查中，也可视为有两个总体：参与网络调查（回答）的总体和没参与网络调查（无回答）的总体。倾向得分可通过对表示某人是否回答的变量进行建模而得到。常常将指示变量（是否回答即R）作为因变量，单元的辅助变量作为解释变量建立Logistic回归模型，这些辅助变量常常用于测量单元的态度、行为或生活形态，且参与者和未参与者的辅助变量值都是已知的。为了实现这一点，可通过在自选式网络调查中采取一定的措施找到看到网上问卷（通过访问网址、电子邮件等）但未回答单元的联系方式，如IP地址、电子信箱、QQ、微信、电话等，对无回答的总体以联系方式为抽样框实施随机抽样调查，调查内容以态度、行为或生活形态等辅助变量为主，同时对自选式网络调查中的回答单元必须提出同样的问题（可将辅助变量相关问题一并放入网上问卷中），从而拟合Lo-gistic回归模型就可估计回答概率，即倾向得分。倾向得分p（X）是一个具有观察到的特征向量X（辅助变量）的人参与网络调查（回答）的条件概率，即p（X）＝P（R＝1｜X）。

假定具有相同辅助变量X值的所有人都有相同的参与倾向，即倾向得分相同，这属于随机缺失的假定。对每一个单元i，这些辅助变量值的向量表示为X＝（X，X，…，X）′，假设这些值对总体的所有单元都是已知的（包括未回答的单元），且X都经过中心化变换，则第i个单元的倾向得分p（X）可通过建立Logistic回归模型来得到，即

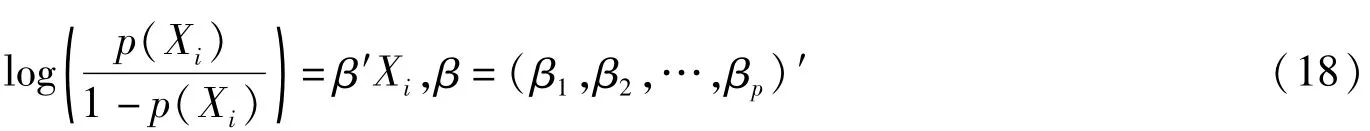
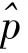
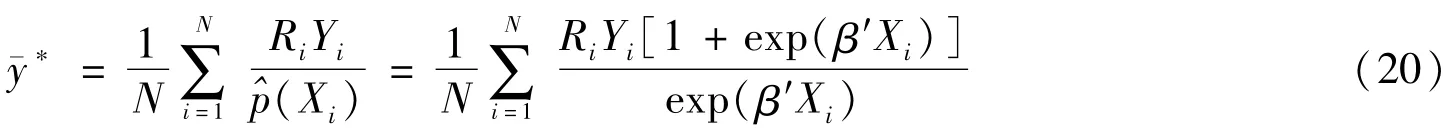
总体总量的估计为：

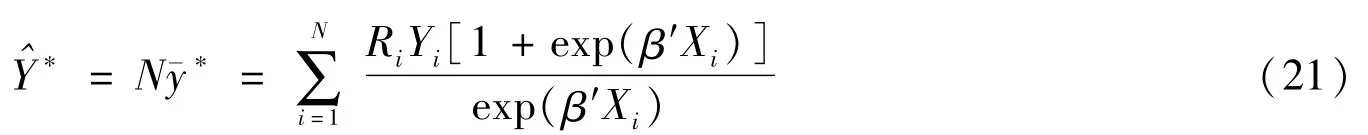
四、结束语

由于自选式网络调查得到的样本为传统意义上的非概率样本，无法采用概率抽样的统计推断理论对自选样本进行统计推断。本文针对自选样本，考虑网络总体，给出自选样本的总体均值、总量的估计，推导证明了估计的性质，并进一步采用倾向得分方法对估计进行加权调整，为网络调查的统计推断提供一定的参考。此外，若目标总体并非网络总体，即还有一些人没有上网但也是调查的对象，此时就会导致覆盖不全的问题，在此种情况下如何进行统计推断，也是值得进一步研究的问题。

［责任编辑 王治国 责任校对 王景周］

【国际法研究】

［基金项目］

中国人民大学科学研究基金资助项目《大数据时代下的样本匹配问题研究》（批准号：15XNH102）。

［作者简介］

刘 展（1981—），女，湖北宜昌人，中国人民大学统计学院博士生，主要从事抽样调查技术与数据分析研究。

［收稿日期］

2015－05－25

［中图分类号］

C811

［文献标识码］

A

［文章编号］

1000－5072（2015）09－0106－06