求常系数线性微分方程解的矩阵方法
2015-03-01赵晓苏钱椿林
赵晓苏,钱椿林
(苏州市职业大学 数理部,江苏 苏州 215104)
求常系数线性微分方程解的矩阵方法
赵晓苏,钱椿林
(苏州市职业大学 数理部,江苏 苏州 215104)
考虑求常系数线性微分方程解的矩阵方法.首先,将常系数线性微分方程化为一阶线性微分方程组,且用矩阵表示;然后,求其矩阵的特征值和特征向量,把矩阵对角化或化简;最后,利用矩阵乘法求得常系数线性微分方程的通解或特解. 其计算方法简单、方便,在实际中很有用.
常系数线性微分方程;矩阵;特征值;特征向量;通解;特解
1 问题的提出
在科学研究和生产实践中往往会碰到某些量之间存在着某种微分关系,其数学表达式为微分方程,例如
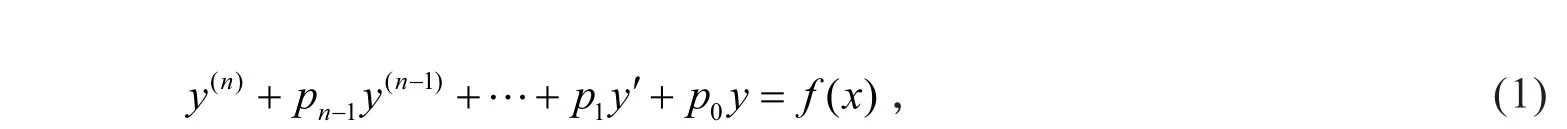
式中:f(x)为已知函数;pi(i=0,1,2,…,n-1)为已知常数;y=y(x)为未知函数.称式(1)为n阶常系数线性微分方程.如果f(x)≠0,称式(1)为n阶非齐次常系数线性微分方程;如果f(x)=0,称式(1) 为n阶齐次常系数线性微分方程,即
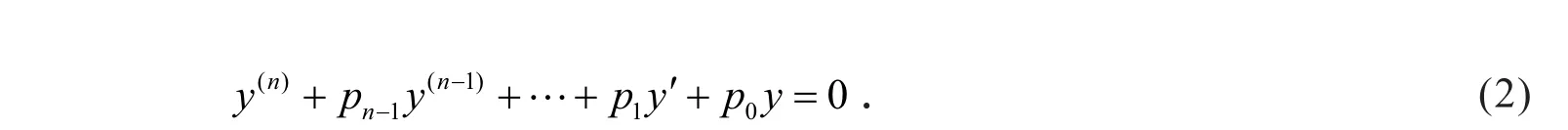
对于n阶非齐次常系数线性微分方程(1)的求解,通常的做法是:讨论非齐次项f(x)的各种类型,利用待定系数法求得一个特解[2-5].对于非齐次项f(x)是一般的情形,用待定系数法显得无能为力.对于一般的非齐次项f(x),利用矩阵方法[1],可以求得其微分方程的一个特解或通解.其计算方法简单、方便,在实际中很有用.本文主要讨论二阶常系数线性微分方程求解的矩阵方法,其方法可以在求任意阶常系数线性微分方程的解中使用.
2 指数矩阵的定义及性质
2) 指数矩阵具有如下性质:
3 问题的解法
求常系数线性微分方程解的矩阵方法的具体步骤如下:
第1步,将常系数线性微分方程(1)化为一阶线性微分方程组,且用矩阵表示.
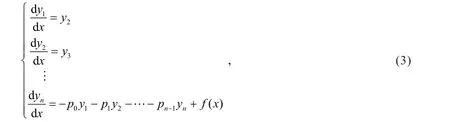
式中y=y1.令,且矩阵
则式(3)可记作

第2步,求A的n个特征值和特征向量.作线性变换Y=PU,其中,P是由A的n个线性无关特征向量组成的n阶可逆方阵,代入式(4),且设D=P-1AP,得
当n=2时,D可以是下列两种简单情形:当λ1≠λ2时
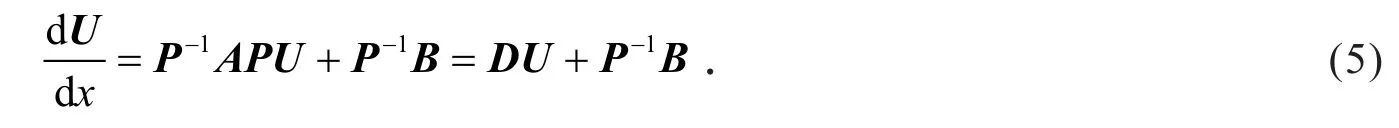
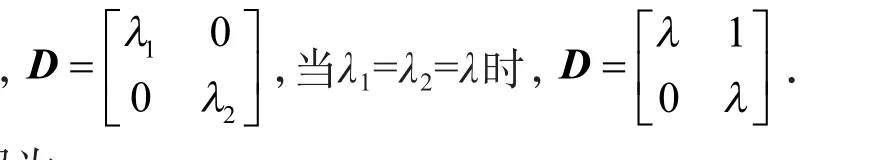
第3步 求得一阶线性微分方程组(5)的特解或通解为

第4步 利用矩阵乘法和式(6)求Y(=PU),取Y的第1行第1列的元素,得到y=y1.
通过具体例子说明用矩阵方法求解常系数线性微分方程的详细计算过程,主要讨论二阶常系数线性微分方程的解的情况.
例1 求微分方程的一个通解.
解第1步,将微分方程化为一阶线性微分方程组,即


第3步,求得一阶线性微分方程组(8)的通解为
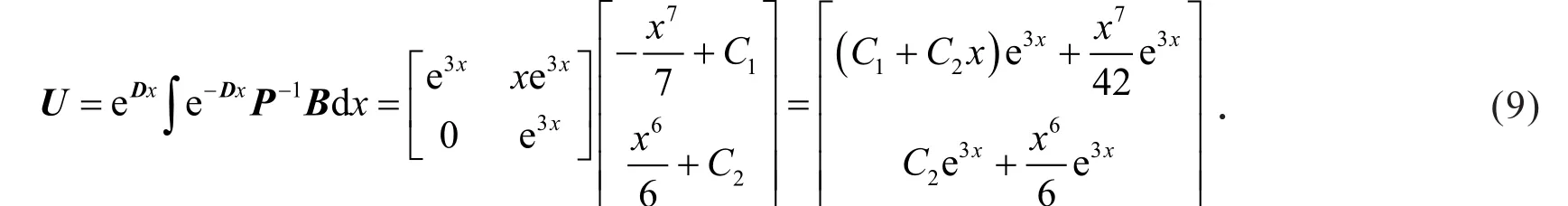
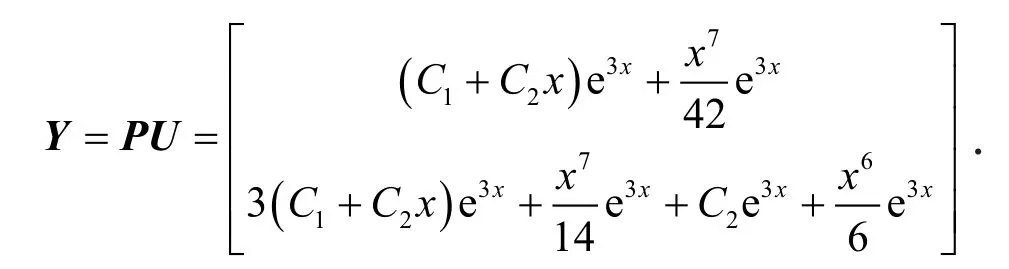
取Y的第1行第1列的元素,得到通解为
例2 求微分方程y′ + y =sec3x的通解.
解第1步,将微分方程化为一阶线性微分方程组,即


第3步,求得一阶线性微分方程组(11)的通解为
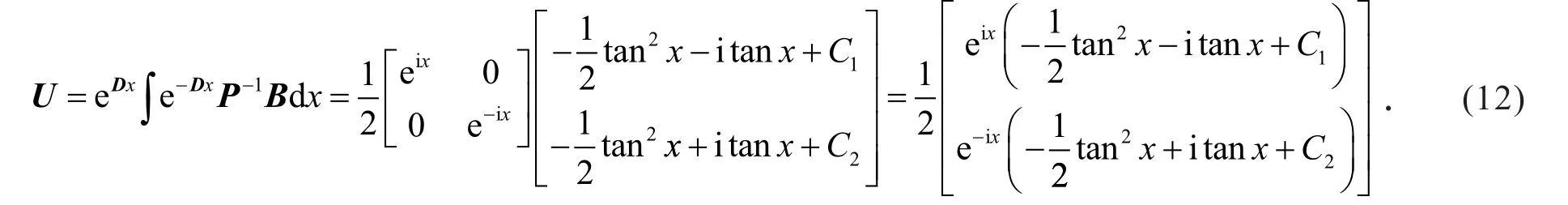
第4步,利用矩阵乘法和式(12)有
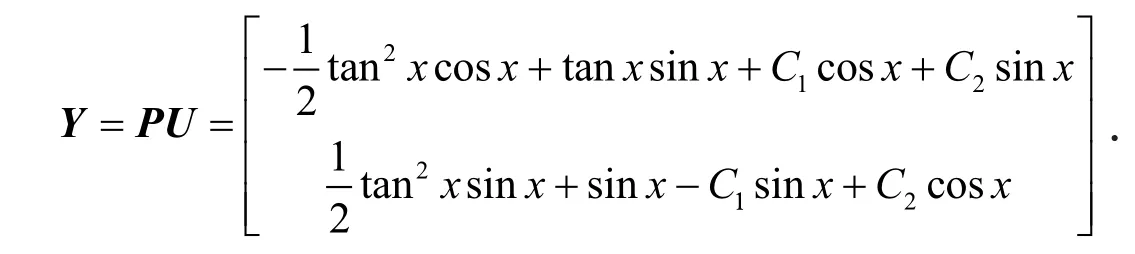
取Y的第1行第1列的元素,得到通解为

例3 求微分方程的一个特解.
解将微分方程化为复数的形式,即

只要考虑微分方程(13)的一个特解的虚部即可
第1步,将微分方程化为一阶线性微分方程组,即


第3步,求得一阶线性微分方程组(15)的特解为
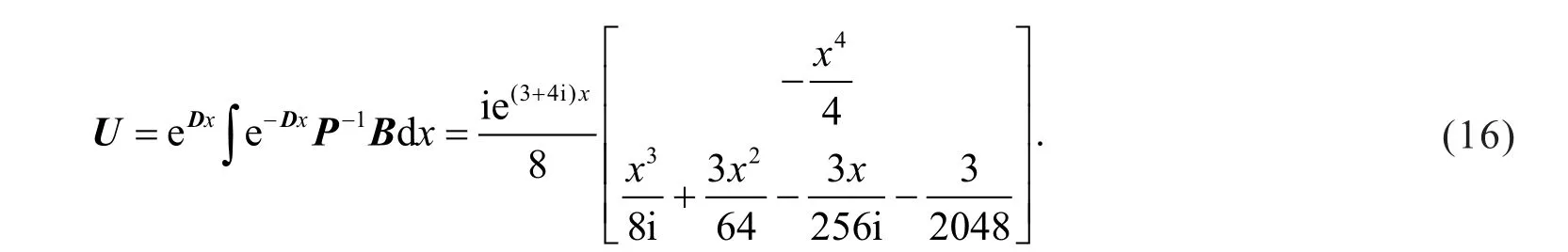
第4步,利用矩阵乘法和式(16)得
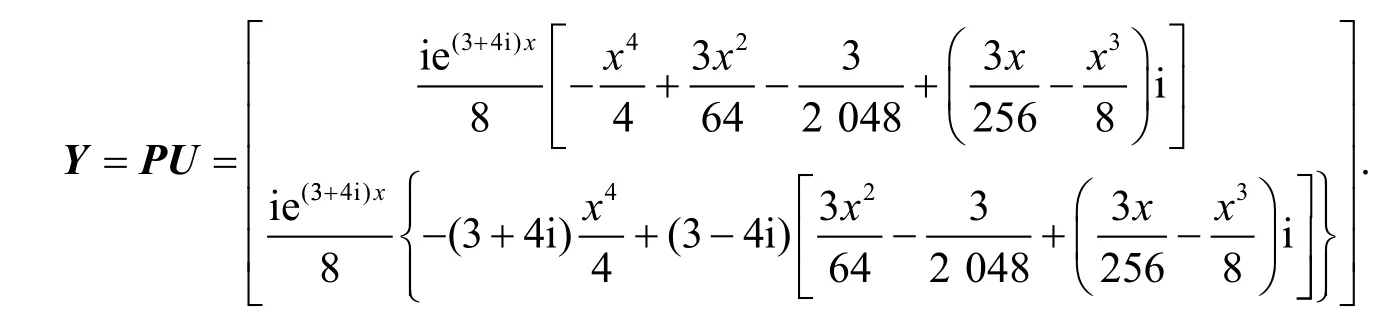
取Y的第1行第1列的元素,得到特解为
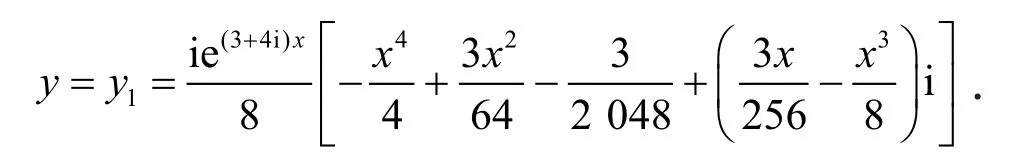
取其解的虚部,得到一个特解为
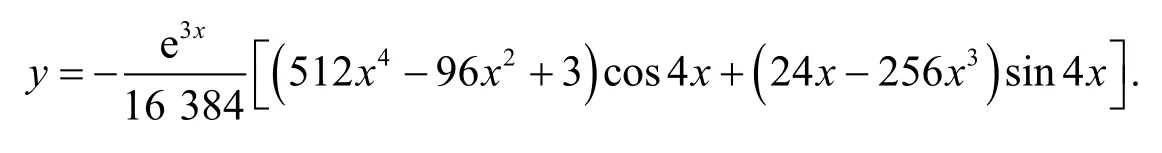
例4 求微分方程
的通解.
解第1步,将微分方程化为一阶线性微分方程组,即


第3步,求得一阶线性微分方程组(18)的通解为
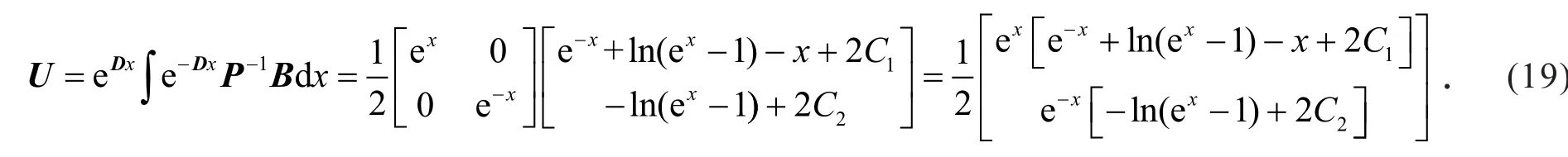
第4步,利用矩阵乘法和式(19)有
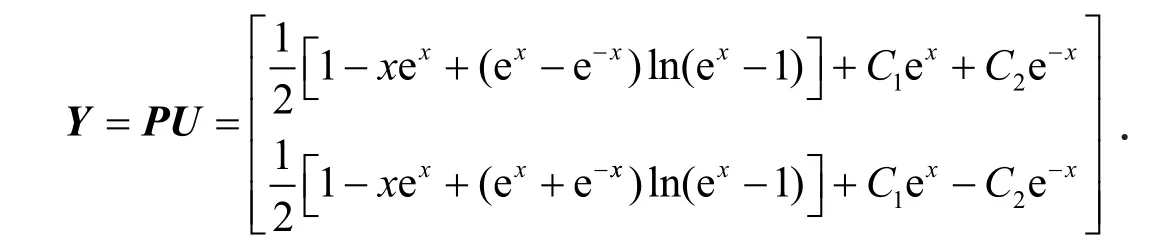
取Y的第1行第1列的元素,得到通解为
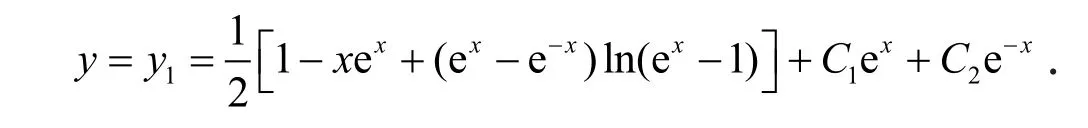
例5 求微分方程的通解.
解第1步,将微分方程化为一阶线性微分方程组,即


第3步,求得一阶线性微分方程组(21)的特解为
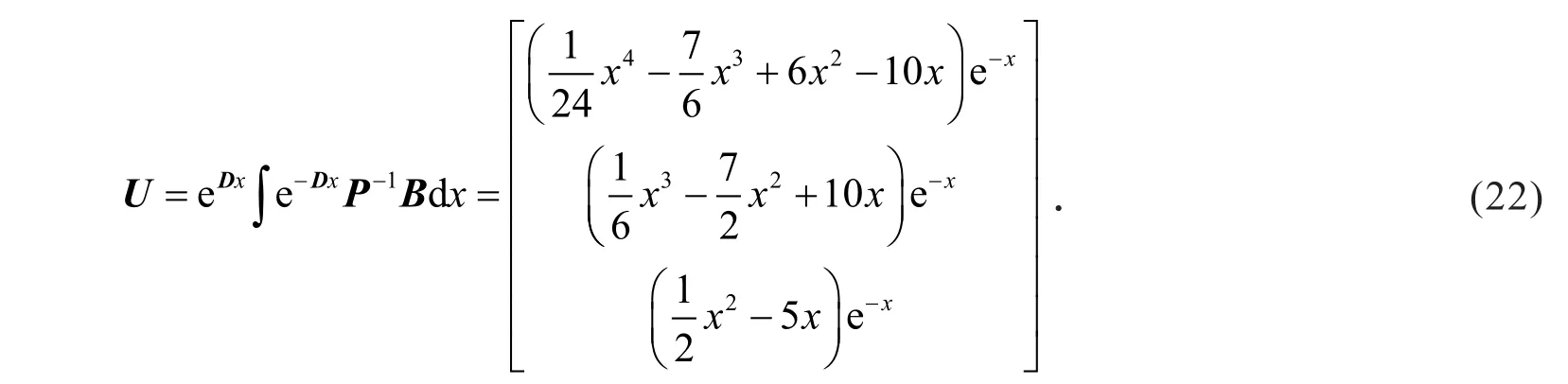
第4步,利用矩阵乘法和式(22),得
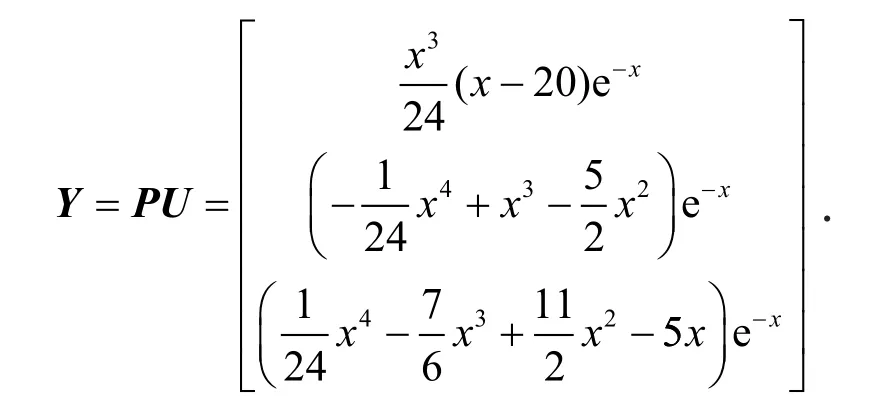
取Y的第1行第1列的元素,得到一个特解为
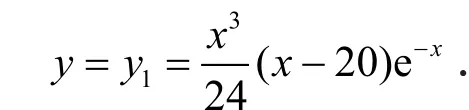
所以通解为
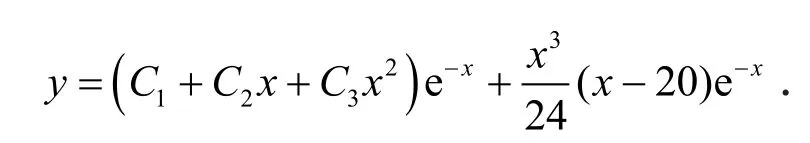
从上面5个例子可以看到,例1、例3和例5是常见非齐次项的微分方程的两种类型,如果利用待定系数法求解,计算量比较大,例2和例4不是常见非齐次项的微分方程的类型,利用待定系数法无法求解,利用矩阵方法计算比较方便.矩阵方法对于一般的非齐次项的常系数线性微分方程都能得到求解,同时给出了一般的非齐次项的常系数线性微分方程求通解的一个公式,即公式(6),因此在实际中很有用.
[1] 钱椿林. 线性代数[M]. 3版.北京:高等教育出版社,2010.
[2] 钱椿林. 高等数学[M]. 3版.北京:电子工业出版社,2010.
[3] 同济大学应用数学系. 高等数学[M]. 5版.北京:高等教育出版社,2004.
[4] 《现代应用数学手册》编委会. 现代应用分析卷[M]. 北京:清华大学出版社,1998.
[5] 《数学手册》编写组. 数学手册[M]. 北京:高等教育出版社,1984.
(责任编辑:沈凤英)
Matrix Method for the Linear Differential Equation with Constant Coeffcients
ZHAO Xiao-su,QIAN Chun-lin
(Department of Mathematics and Physics,Suzhou Vocational University,Suzhou 215104,China)
The paper addresses matrix method for the linear differential equation with constant coeffcients. First of all,the system of the frst order linear differential is the linear differential equation with constant coeffcients transformed into the first order linear differential group,and presented by matrix,and then eigenvalue and eigenvector of the matrix,is obtained while the matrix is transformed into simplified matrix. Finally,the solution of the linear differential equation is achieved using the matrix multiplication. It is found that this method provides an easier and more useful solution to the linear differential equation with constant coeffcients.
linear differential equation with constant coefficients;matrix;eigenvalue;eigenvector;general solution;special solution
O151.26
A
1008-5475(2015)01-0044-06
2014-09-03;
2014-10-02
赵晓苏(1962-),女,江苏苏州人,副教授,主要从事算子特征值估计研究.
