Kantorovich 型 Bernstein-Stancu 算子的点态逼近
2015-03-01董吕修虞旦盛
董吕修,虞旦盛
(杭州师范大学理学院,浙江 杭州 310036)
Kantorovich 型 Bernstein-Stancu 算子的点态逼近
董吕修,虞旦盛
(杭州师范大学理学院,浙江 杭州 310036)
摘要:针对öz 引入的一种 Kantorovich 型 Bernstein-Stancu 算子及其逼近的正定理,文章进一步推广了相关结论, 并建立了点态的逼近正、逆定理.
关键词:Bernstein-Stancu 型算子;点态与整体估计;正、逆定理
0引言

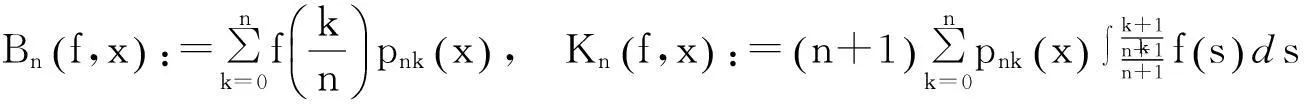
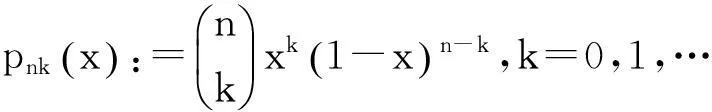
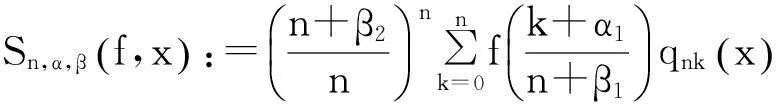
(1)

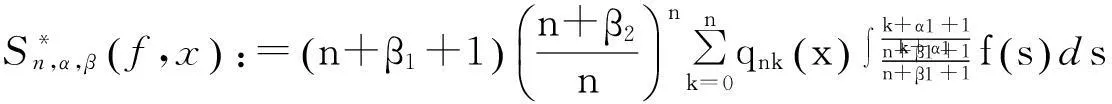


本文的首要目的就是在移动区间An上建立一个包含点态估计与整体估计的正定理. 为陈述本文结果,需要以下概念和记号:
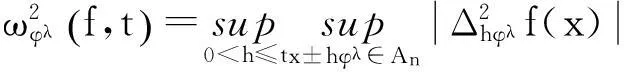
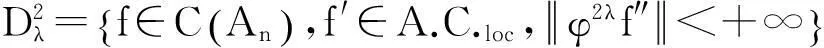
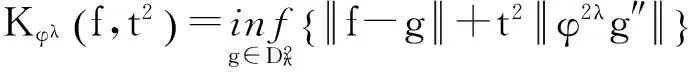
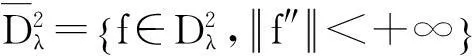
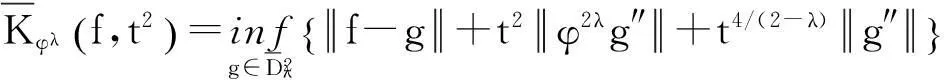
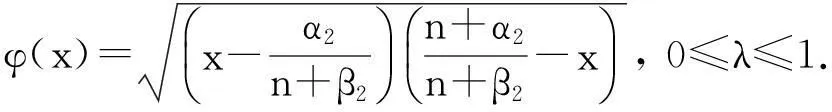

(2)
这里x~y表示存在正常数c使得c-1y≤x≤cy.
本文的结论如下:

贯穿全文,C或者表示一个绝对正常数,或者表示一个依赖于某些参数但不依赖于f,x,n的正常数.它们的值在不同的地方可以不同.
对于逆定理,有
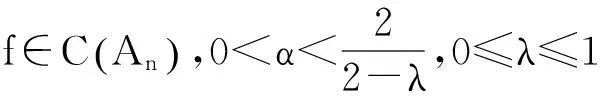
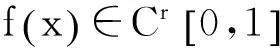
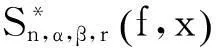
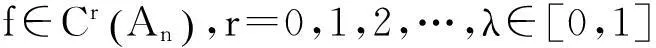
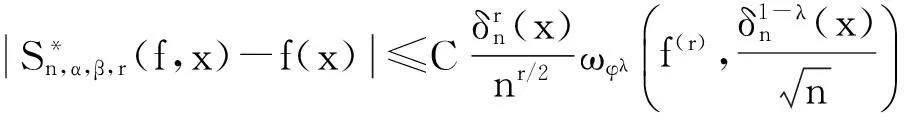
1预备引理
引理1[7]对于任意给定的γ≥0,成立不等式
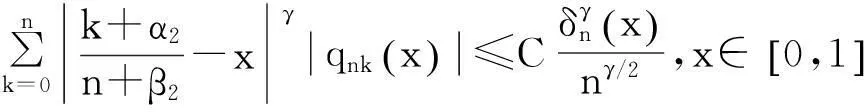
(3)
引理2对于任意的x∈An,有
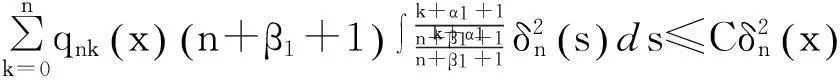
(4)
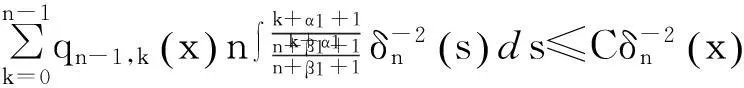
(5)
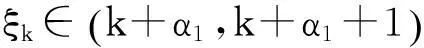
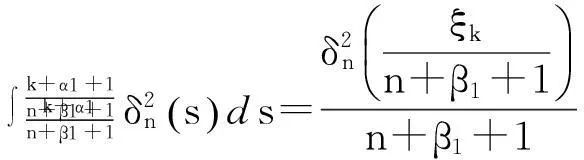
(6)
另一方面,有
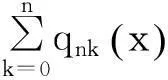
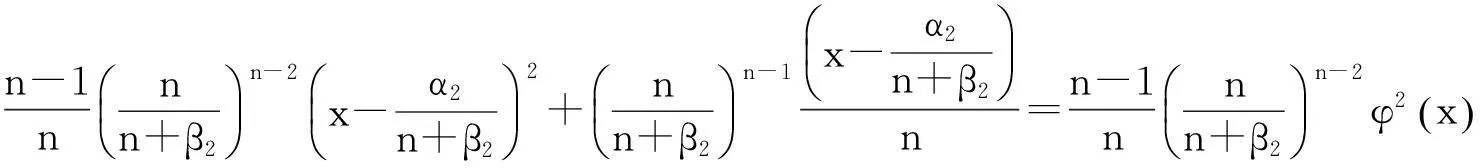
因此,由式(3) 和(6),可以推出
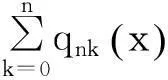

这就证明了式(4).
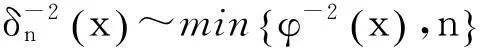
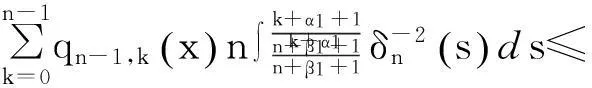
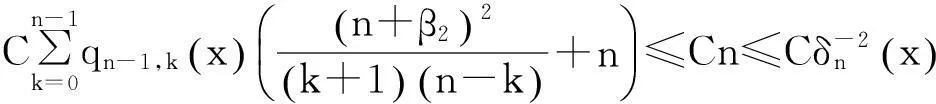
这就证明了式(5).
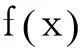

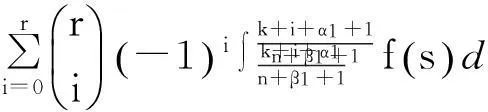
(7)
证明由Leibniz 公式,有

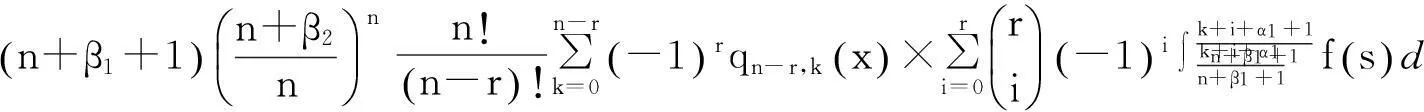
证毕.
令
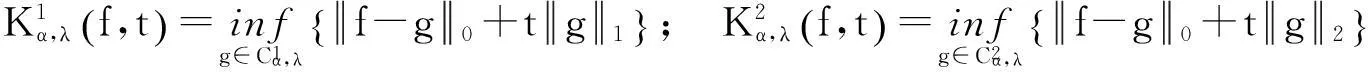
引理4如果 0≤λ≤1,0<α<2,那么
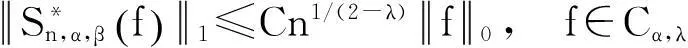
(8)

(9)
证明首先,证明式(8). 考虑以下两种情形.
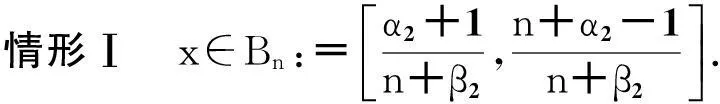
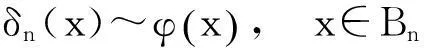
(10)
简单计算可得
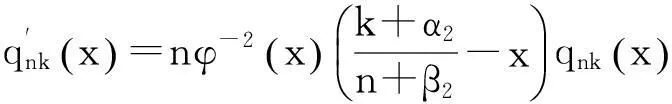
(11)
由式(10),(11) 以及 Hölder 不等式,有
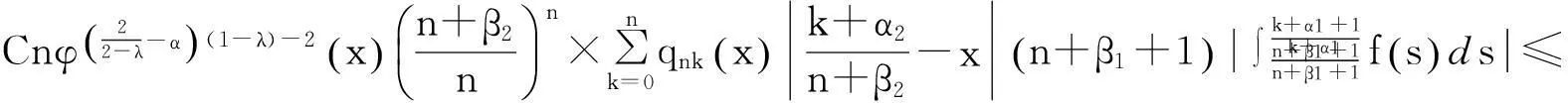
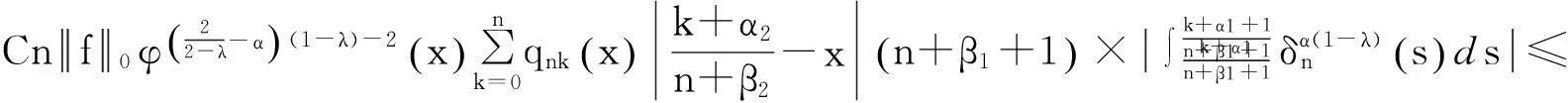
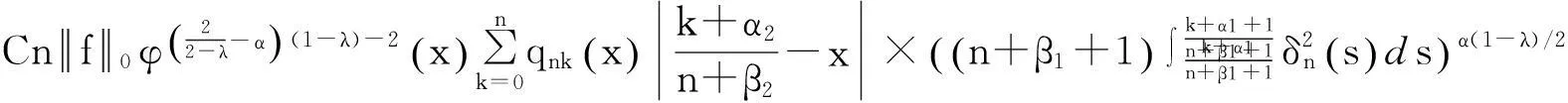
由式(3),(4),(10),并再次利用Hölder不等式,有
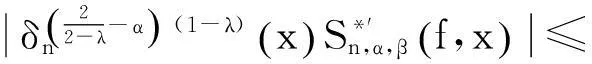
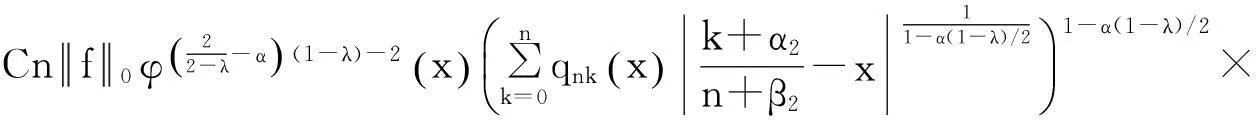
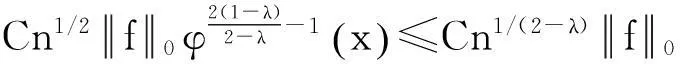
(12)
情形Ⅱ此时,有
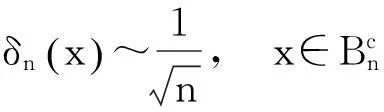
(13)

(14)
由式(3),(13),(14) 以及Hölder不等式,得到

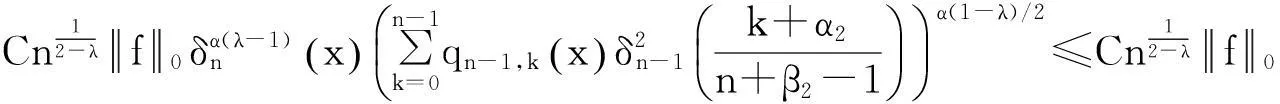
(15)
结合式(12)与(15),式(8)得证.

(16)
由式(16)及Hölder不等式,可得

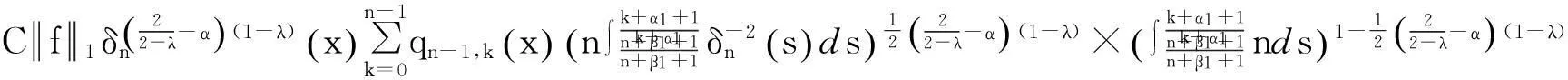
再利用Hölder不等式,有
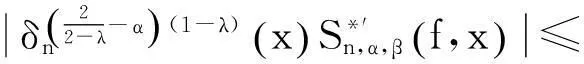
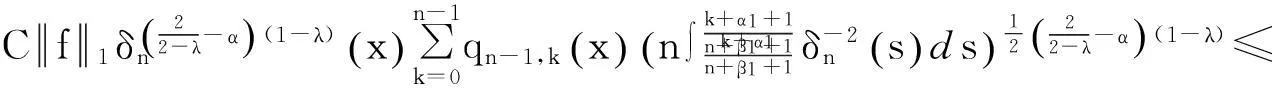
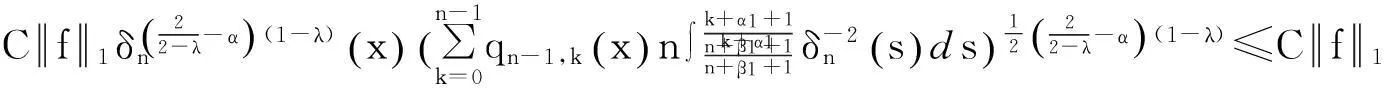
其中在最后一个不等式中利用了式(5).

引理5如果 0≤λ≤1, 0<α<2, 那么
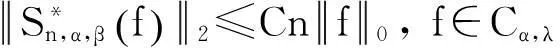
证明证明方法类似于引理 4,在此略去详细过程.
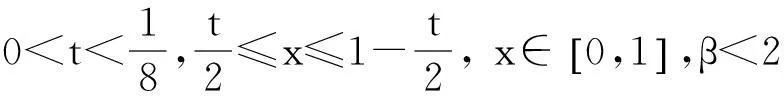

引理8对于每一个m∈N,以下不等式成立:
证明利用积分中值定理,有
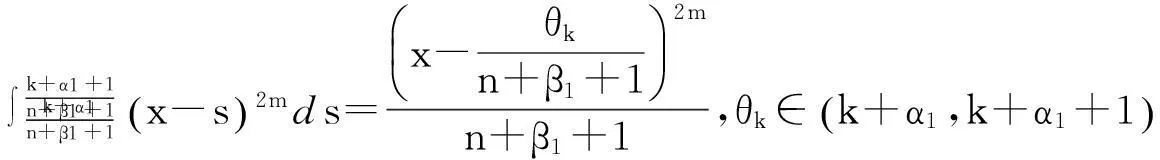
(17)
由式(17)与(3),可以得到
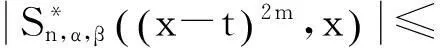
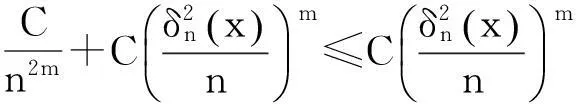
2定理的证明
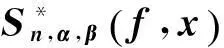
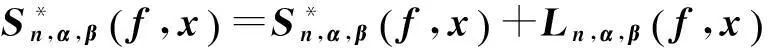
(18)
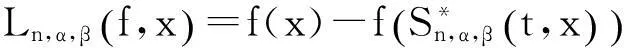
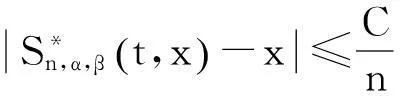
(19)
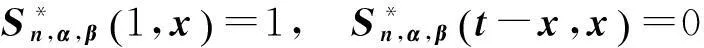
(20)
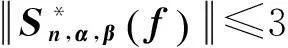
(21)
利用式(19)可以推出
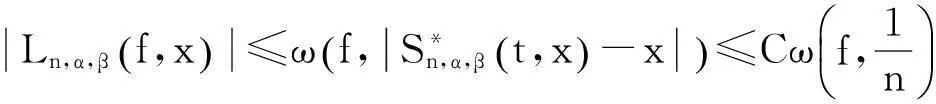
(22)
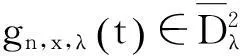

(23)
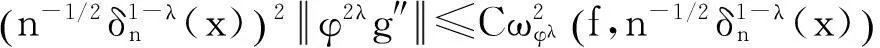
(24)
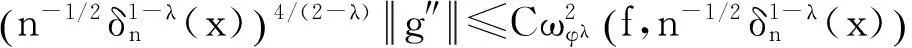
(25)
由式(21)与(23),可得
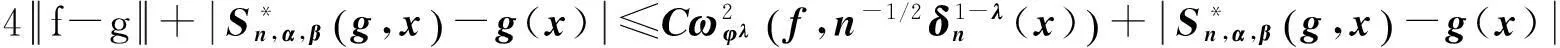
(26)
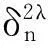
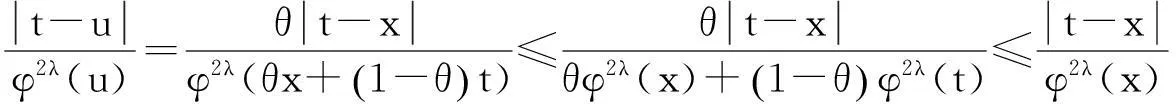
(27)
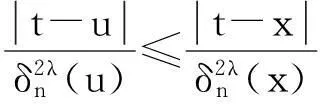
(28)
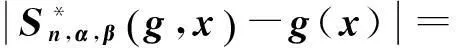
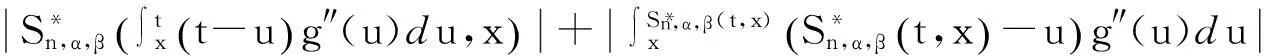
当x∈Bn时,由式(10),(27),(19)以及引理8,有
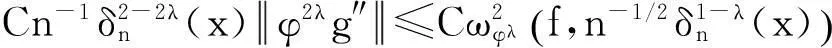
(29)
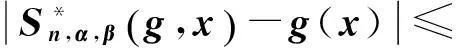

(30)
其中在最后一个不等式中利用了式(24)与(25) .
结合式(18),(22),(26),(29)以及(30),定理1得证.
定理2的证明类似于文献[8]的证明方法,由引理5,6,7,即可完成定理2的证明. 此处省略具体细节.
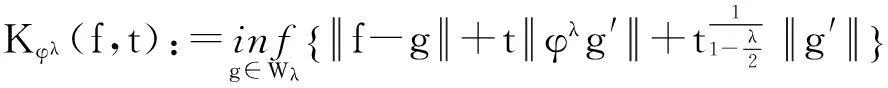
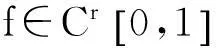

(31)

(32)

(33)
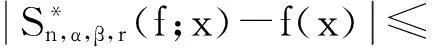

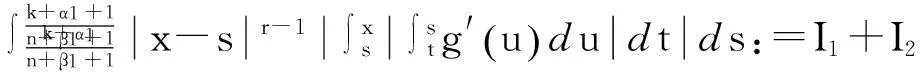
(34)
对于一切x∈An.
由Hölder不等式以及引理8,有

(35)
因此,由式(31),(35)与引理8,可得

(36)
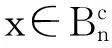
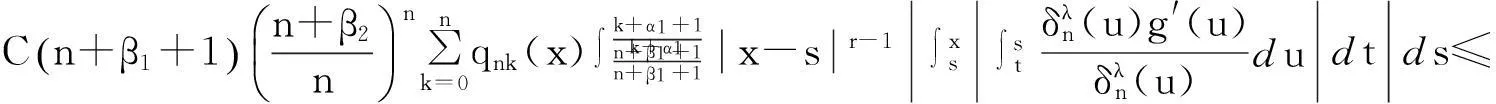
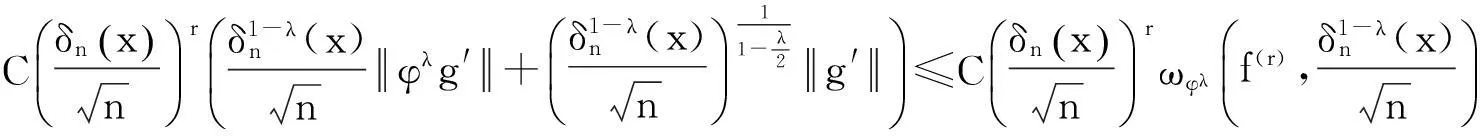
(37)
当x∈Bn时,由式(10),(32),(35)与引理8,可得

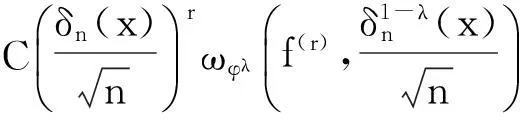
(38)
结合式(34),(36)~(38),定理3得证.
参考文献:
[1] Gadjiev A D, Ghorbanalizaeh A M. Approximation properties of a new type Bernstein-Stancu polynomials of one and two variables[J]. Appl Math Comput,2010,216(3):890-901.
[2] Stancu D D. Approximation of functions by a new class of linear polynomial operators[J]. Rev Roum Math Pure Appl,1968,13(8):1173-1194.
[4] Ditzian Z, Totik V. Moduli of smoothness[M]. New York: Spring-Verlag,1987.
[5] Kirov G, Popova L. A generalization of the linear positive operators[J]. Math Balkanica,1993,7:149-162.
[7] Wang M L, Yu D S, Zhou P. On the approximation by operators of Bernstein-Stancu type[J]. Appl Math Comput,2014,246(1):79-87.
[8] Guo S S, Liu L X, Liu X W. The pointwise estimate for modified Bernstein operators[J]. Stud Sci Math Hung,2001,37(1):69-81.
Pointwise Approximation of Kantorovich Type Bernstein-Stancu Operators
DONG Lyuxiu, YU Dansheng
(School of Science, Hangzhou Normal University, Hangzhou 310036, China)
Abstract:Recently, öz introduced a new type of Kantorovich type Bernstein-Stancu operators, and obtained a direct theorem about approximation. The present paper further generalized öz’s results, and established the direct and converse theorems about pointwise approximation.
Key words:Bernstein-Stancu type operators; pointwise and global estimates; direct and inverse theorems
文章编号:1674-232X(2015)06-0632-09
中图分类号:O174.41MSC2010: 41A25; 41A35
文献标志码:A
doi:10.3969/j.issn.1674-232X.2015.06.013
通信作者:虞旦盛(1976—),男,教授,主要从事函数逼近论研究.E-mail:dsyu_math@163.com
收稿日期:2015-01-09
