一类扰动复Swift-Hohenberg方程的精确孤立子解

龙林园,杨立新,徐衍聪

(1.杭州师范大学理学院,浙江 杭州 310036；2.浙江同济科技职业学院数理学院,浙江 杭州 311231)

一类扰动复Swift-Hohenberg方程的精确孤立子解

龙林园1,杨立新2,徐衍聪1

(1.杭州师范大学理学院,浙江 杭州 310036；2.浙江同济科技职业学院数理学院,浙江 杭州 311231)

摘要：利用Painlevé分析、Hirota多元线性法和直接拟设技巧，研究了一维带有耗散项的五次复Swift-Hohenberg方程的解析解.找到了方程的精确解并证明方程系数之间存在着某种关系.得到了包括特殊类型的孤波解、暗孤子解和以雅可比椭圆函数形式表示的周期解等，为光学的进一步研究提供了一系列孤子解.

关键词：孤立子;Painlevé分析;Hirota多元线性法;Swift-Hohenberg方程;直接拟设法

0引言

Swift-Hohenberg方程首先由Swift等[1]提出，主要用于描述局部结构和现代物理学的各种斑图形成现象[2-3],包括Taylor-Couette 流中的Rayleigh-Benard 问题[4]、大规模流和螺旋芯的不稳定性[5]及一些化学反应[6]. 研究的方程看上去复杂，但实际上，斑图空间是由一定数量有序或混乱的简单的局部结构组合在一起所形成的空间.众所周知，Swift-Hohenberg方程服从横向局部结构和相域的存在性[7].这些相关的结构可以视为亮、暗孤子.因此，这些简单的局部结构及其稳定性，在研究任何斑图形成的系统时能引起学者的浓厚兴趣.考虑到斑图直观的特性，可以将问题分成几个步骤.首先，应当掌握最基本的固定对象(局部结构).然后，必须分析其稳定性.最后，应该研究它们之间的相互作用和组合结构.此外，为了更多的稳定局部结构的研究，应该从最简单的情况开始，即(1+1)维结构.按照这个顺序逐步进行，可以防止在试图一步解释一个复杂的内部结构时出现任何可能的混淆.

在许多方面，Swift-Hohenberg方程的局部结构类似于先前研究的复Ginzburg-Landau方程(CGLE).回顾一些经典的五次CGLE的解析解[8-11],S-H 方程[12]与CGLE的主要区别在于它涉及衍射项.在描述一个实际物理问题的详细特征时，后者显得尤为重要.在三次(1+1)维方程的例子中，解析解描述了所有可能的亮孤子和暗孤子解.但是五次方程中，CGLE的解析解仅表示很小一部分的孤子解，并且其中还不包含稳定的孤子解[11].

众所周知，除了一些例外，CGLE通常只有孤立解[11,13]，即对任意特定的方程参数，它的解是奇异的.更一般地，孤立解的存在性是耗散系统的一个基本特征，该特征具有定性的物理基础[14].Swift-Hohenberg方程模型的耗散系统与CGLE相似，并且预计它也将有此特征.事实上，初步的数值模拟支持了这一猜想.在物理问题中，五阶非线性等同甚至超过三阶[15]的重要性，因为它决定了局部解的稳定性.笔者将分析(1+1)维亮孤子和暗孤子，并先暂时不考虑它们的稳定性和它们之间的相互作用问题.本文研究了含耗散项的五次Swift-Hohenberg方程，并且利用Painlevé和Hirota多元线性方法得到新的精确解.此方法是Berloff-Howard法[16]的修改和延伸，并最早由Nozaki等[17]提出.除此之外，将通过直接拟设法来确认所得的解是成立的.在这里得到的解可作为进一步研究的基础.笔者研究的一维五次含有耗散项的复Swift-Hohenberg方程为：

iut+βuxx+γuxxxx+μ|u|2u+ν|u|4u+ε|ux|2u=iδu,

(1)

方程中的系数β=β1+iβ2，γ=γ1+iγ2，μ=μ1+iμ2，ν=ν1+iν2和ε=ε1+iε2为复数，δ为实数.

参数的实际意义取决于具体的物理问题.在激光光学系统的问题中，t表示传播距离或腔的往返次数(作为一个连续变量)，x表示延迟时间，β1表示二阶色散，γ1表示四阶衍射，μ2表示非线性增益(若μ2为负数，则表示双光子吸收)，δ则表示联合线性增益和耗损.带限增益则由β2(抛物型的光谱形状)，γ2(4阶校正)和ε|ux|2u(耗散项)表示.

本文余下部分组织结构如下：首先，回顾本文将使用的方法和分析程序；随后，对带耗散项的CQSH方程进行Painlevé分析，并得到它在特殊情况下的精确解；最后,总结出结论.因为没有必要的参数很小，所以不受扰动机制的限制.

1方法论

1.1　Painlevé分析和Hirota多元线性法

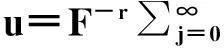
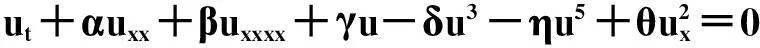
(2)

并说明如何通过Painlevé检验和Hirota多元线性法，得到含耗散项的不可积偏微分方程的精确解.把变换截断在常数项之前，

u=u0F-r+u1F-r+1+…+um-1F-1.

(3)

对首项指数的分析得 r=1.将展式(3)代入RQSH方程(2)中，并令F最高阶项的系数为0，可得u0的关于F的表达式，并且有

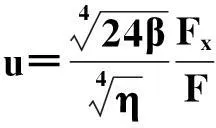
(4)

将变换(4)代入式(2)可得一个关于F的四次方程：

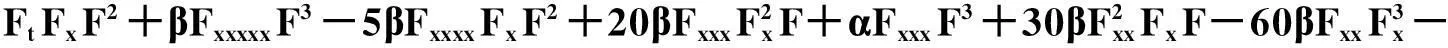
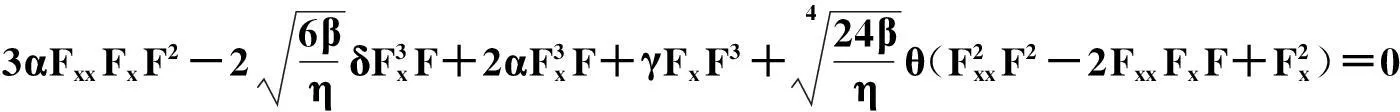
(5)

然后，将F=1+e2kx+2ωt代入四次线性方程(5)中，合并同类项并使含不同幂e项的系数为零，便能够得到4个代数方程，但该方程组没有解. 现在，做另外一个不同的假设变换：

(6)

然后，将变换(6)代入方程(5)中，能够得到一个关于F和G的五次线性方程：

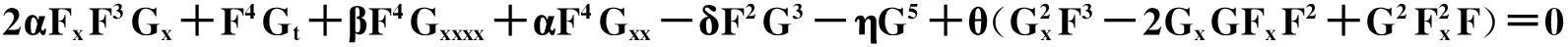
(7)

如果将 F=1+e2kx+2ωt，G=ne2kx+2ωt+2mekx+ωt+n代入方程(7)中，合并同类项并使含不同幂e项的系数为零，能够得到单孤子解：

u=msech(kx)+n,

(8)

其中，

如果将F=1+e2kx+2ωt，G=(n+m)e2kx+2ωt+n-m代入方程(7)中，合并同类项并使含不同幂e项的系数为零，能够得到扭结解：

u=mtanh(kx)+n,

(9)

其中，

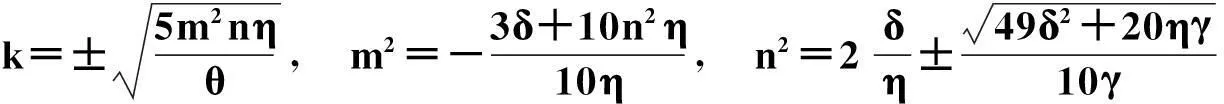
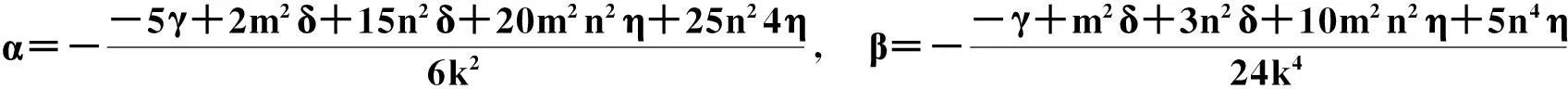
1.2　直接拟设法

许多非线性微分方程的解可以通过双曲函数表示.这一事实促使了一种直接的方法，它的出发点是作出一个合适的拟设，使偏微分方程可表示为一个关于双曲正切tanh函数和双曲正割sech函数的多项式.当找不到合适的拟设时，这种方法就失去了意义，所以它不像Hirota法一样具有一般性.但这种方法比Hirota方法更简单，更易获得周期解(椭圆函数的形式).利用此方法得到方程(3)的椭圆解如下：

1.2.1Jacobi cn函数

u=mcn(kx,q)+n,

(10)

其中，

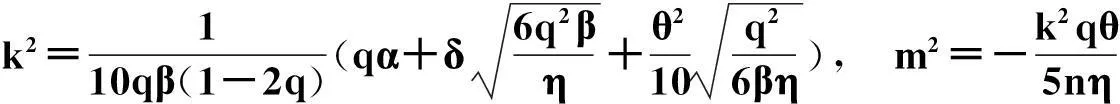
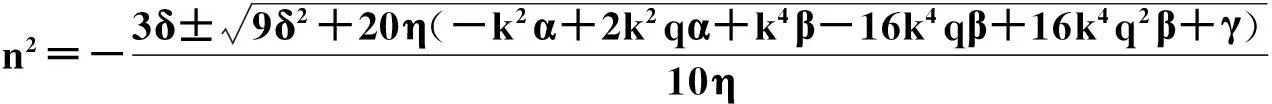
1.2.2Jacobi sn函数

u=msn(kx,q)+n,

(11)

其中，

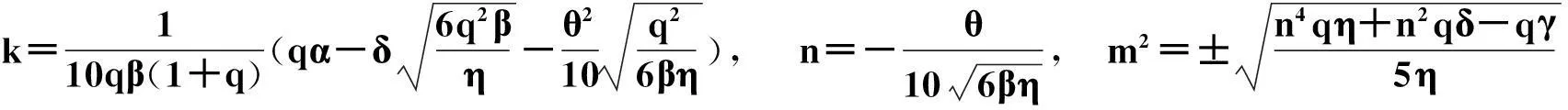
1.2.3Jacobi dn函数

u=mdn(kx,q)+n,

(12)

其中，

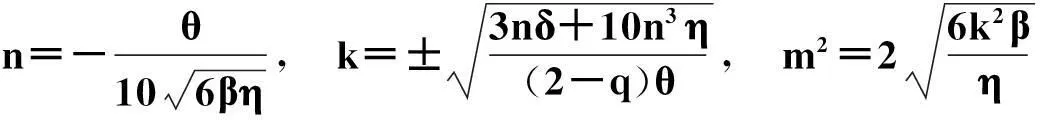
2复S-H方程的Painlevé分析

五次复Swift-Hohenberg方程首先改写为如下方程：

iut+(β1+iβ2)uxx+(γ1+iγ2)uxxxx+(μ1+iμ2)|u|2u+(ν1+iν2)|u|4u=iδu,

(13)

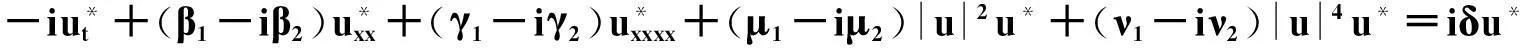
(14)

u和u*的展开形式为：

u=(u0F-1-iα+u1F-iα+…)exp(iKx+iΩt),

(15)

(16)

并且，可以采取以下相关变量变换：

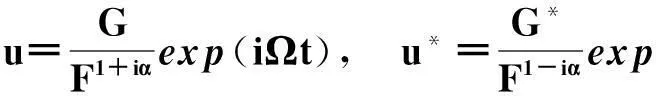
(17)

3含有耗散项的五次复S-H方程的精确解

这里讨论的含有耗散项的五次复S-H方程的形式为：

iut+(f+2id)uxx+iduxxxx+(b2-ib1)|u|2u+(-c2+ic1)|u|4u+

(m2-im1)|ux|2u=(-a2+i(a1-d))u,

(18)

然后将变换(17)代入方程(18)中，得：

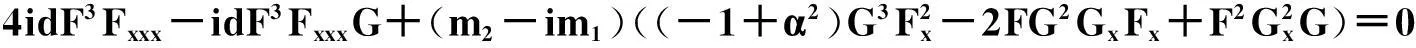
(19)

把F，G和G*写成exp(kx+ωt)的多项式形式，并将这些函数代入方程(19)中，可得如下精确解(也能通过直接拟设法得到相同的解)：

3.1　亮孤子

u=gsech(kx)eiΩt,

(20)

这里，

且方程系数满足的限制关系是：

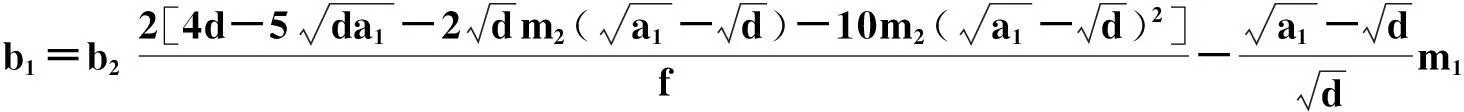
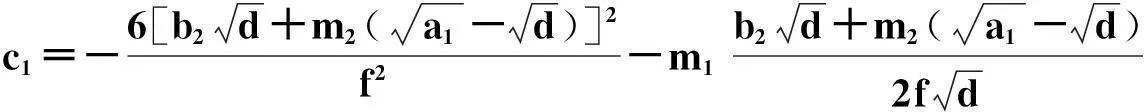
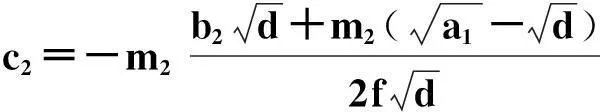
3.2　暗孤子

u=gtanh(kx)eiΩt,

(21)

这里，

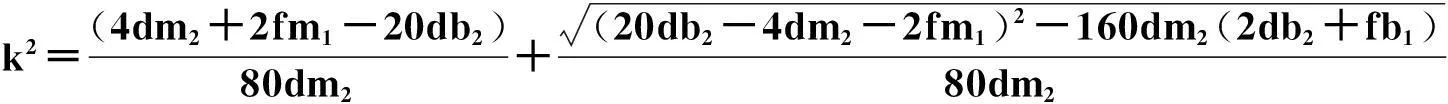
且方程系数满足的限制关系是：

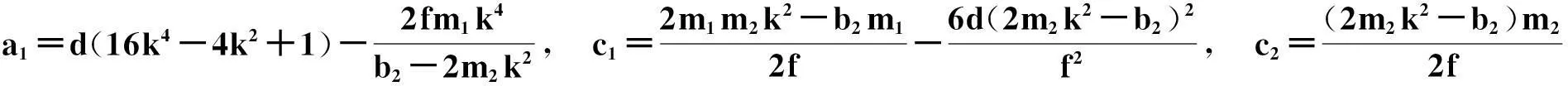
3.3　啁啾亮孤子

u=gsech(kx)e-iαlog(sech(kx))eiΩt,

(22)

这里，

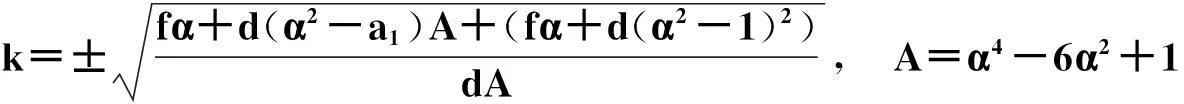
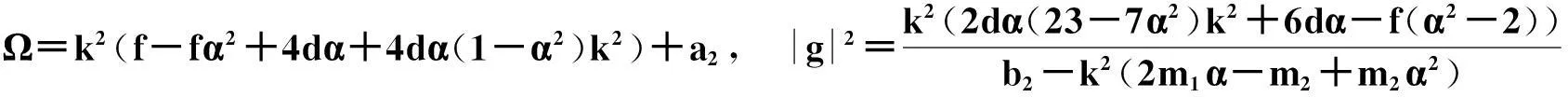
且方程系数满足的限制关系是：

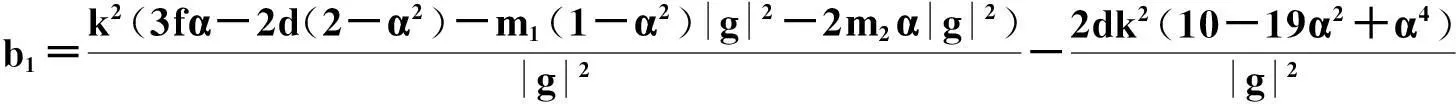
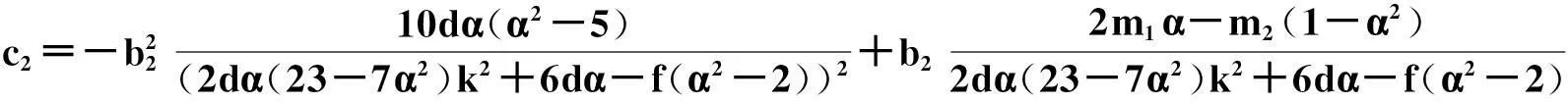
3.4　啁啾暗孤子

u=gtanh(kx)e-iαlog(sech(kx))eiΩt,

(23)

这里，

A=-2b1(5α(8+α2)-α(16-15α2)m1+(16-15α2)m2)-2b2(20-25α2-16-15α2m1-α(16-15α2)m2),

B=b1(2f+6dα-fα2-(8dα-6fα2)m1+(8d-6fα)m2)+b2(4d-3fα-2dα2-(8d-6fα)m1-(8dα-6fα2)m2),

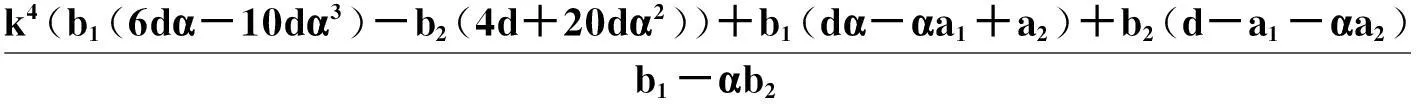
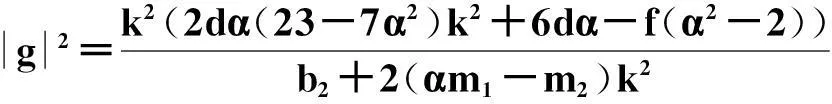
且方程系数满足的限制关系是：

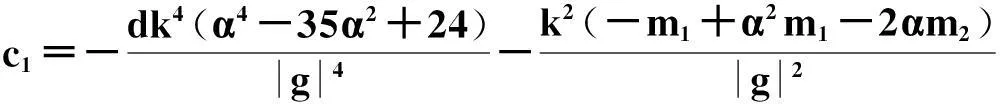
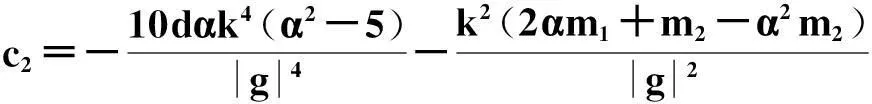
方程的椭圆函数解如下：

3.4.1 雅可比cn函数解

u=gcn(kx,m)eiΩt,

(24)

其中，

A=-24mc2(m1-mm1)-(c1m2-c2m1)(16m2-16m+1),

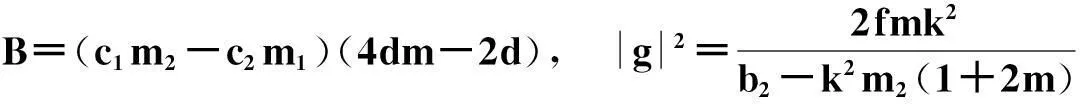
且方程系数满足的限制关系是：

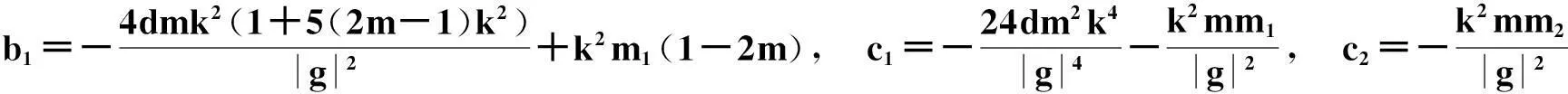
3.4.2雅可比sn函数解

u=gsn(kx,m)eiΩt,

(25)

其中,

A=-24mc2m1+(c2m1-c1m2)(m2+14m+1),

B=-2d(c2m1-c1m2)(1+m),

且方程系数满足的限制关系是：

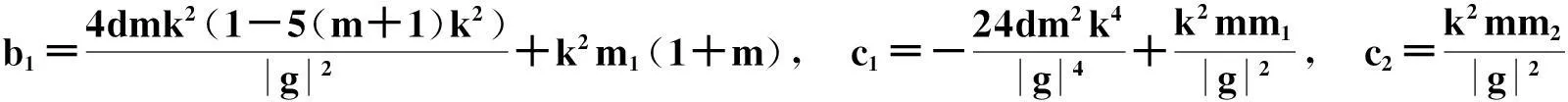
3.4.3雅可比dn函数解

u=gdn(kx,m)eiΩt,

(26)

其中，

A=-24c2m1(1-m)+(c2m1-c1m2)(m2-16m+16),

B=2d(c2m1-c1m2)(2-m),

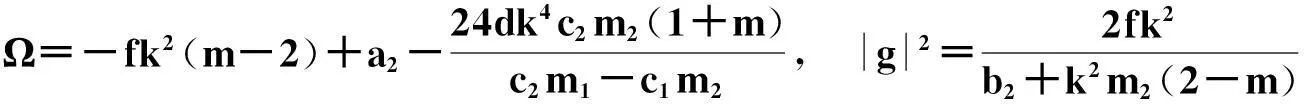
且方程系数满足的限制关系是：

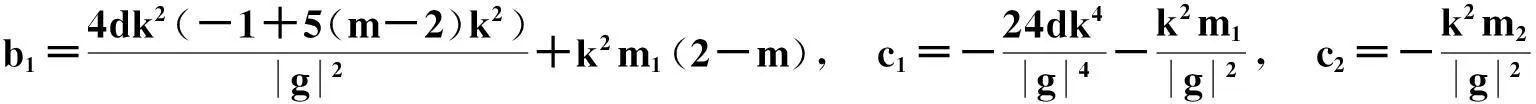
4结论

通过Painlevé分析，利用Hirota多元线性法和直接拟设技巧得到了推广的Swift-Hohenberg 方程的诸多精确解，同时也证明了方程系数之间存在的相互限制关系.然而，这些雅可比椭圆函数形式的解，仅仅代表了所研究方程可能存在的部分周期解和局部解.值得一提的是，本文得到的很多解是孤立子解和周期解，它们构成一系列解族且其参数具有一般性.笔者同时也希望这些解能够为后续的研究提供一定的理论基础.

参考文献:

[1] Swift J B, Hohenberg P C. Hydrodynamic fluctuations at the convective instability[J]. Physics Review A,1977,15(1):319-328.

[2] Cross M C, Hohenberg P C. Pattern formation outside of equilibrium[J]. Rev Mod Phys,1993,65(3):851-1112.

[3] Buceta J, Lindenberg K, Parrpndo J M R. Stationary and oscillatory spatial patterns induced by global periodic switching[J]. Phys Rev Lett,2002,88:024103.

[4] Hohenberg P C, Swift J B. Effects of additive noise at the onset of Rayleigh-Bénard convection[J]. Phys Rev A,1992,46(8):4773-4785.

[5] Aranson I, Assenheimer M, Steinberg V,etal. Large-scale flow and spiral core instability in Rayleigh-Bénard convection[J]. Physical Review E,1997,55(5):4877-4880.

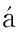
[7] Snchez-Morcillo V J, Staliunas K. Stability of localized structures in the Swift-Hohenberg equation[J]. Physical Review E,1999,60(5):6153-6156.

[8] Pereira N R, Stenflo L. Nonlinear Schrödinger equation including growth and dumpling[J]. Phys Fluids,1977,20:1733-1734.

[9] Saarloos W, Hohenberg P C. Fronts, pulses, sources and sinks in generalized complex Ginzburg-Landau equations[J]. Physica D:Nonlinear Phenomena,1992,56(4):303-367.

[10] Bekki N, Nozaki K. Formations of spatial patterns and holes in the generalized Ginzburg-Landau equation[J]. Phys Lett A,1985,110(3):133-135.

[11] Akhmediev N N, Ankiewicz A. Solitons: nonlinear pulses and beams[M]. London: Chapman & Hall,1997.

[12] Sakaguchi H, Brand H R. Localized patterns for the quintic complex Swift-Hohenberg equation[J]. Physca D： Nonlinear Phenomena,1998,117(1):95-105.

[13] Akhmediev N, Boardman A D, Sukhorukov A P. Soliton-driwen photonics[M].Dordrecht:Kluwer Academic Publishers,2001:371-395.

[14] Akhmediev N, Ankiewicz A, Trillo S,etal. Spatial solitons[M]. Berlin: Springer,2001：311-313.

[15] Moores J D. On the Ginzburg-Landau laser mode-locking model with fifth-order saturable absorber term[J]. Optics Commun,1993,96(1):65-70.

[16] Berloff N G, Howard L N. Solitary and periodic solutions of nonlinear nonintegrable equations[J]. Stud Appl Math,1997,99(1):1-24.

[17] Nozaki K, Bekki N. Exact solutions of the generalized Ginzburg-Landau equation[J]. J Phys Soc Jpn,1984,53(5):1581-1582.

[18] Ablowitz M J, Clarkson P A. Solitons, nonlinear evolution equations and inverse scattering[M]. Cambridge: Cambridge University Press,1991.

Exact Soliton Solutions for the Dimensional Complex Quintic

Swift-Hohenberg Equation with a Dissipative Term

LONG Linyuan1, YANG Lixin2, XU Yancong1

(1.School of Science, Hangzhou Normal University, Hangzhou 310036,China;

2.College of Science, Zhejiang Tongji Vacational College of Science and Technology, Hangzhou 311231,China)

Abstract:Analytic solutions for the dimensional quintic complex Swift-Hohenberg equation with a dissipative term are investigated by using Painlevé analysis,the Hirota multi-linear method and a direct ansatz technique. This paer finds exact solutions exist to the equation and proves that there is certain relation among the coefficients. The set of solutions consist of particular types of solitary wave solutions, dark soliton solutions and periodic solutions in terms of elliptic Jacobi functions are obtainde. In fact,these muliti-parameter families of solutions can act as a seeding set of solutions which can be very useful in optical studies.

Key words:soliton; Painlevé analysis; Hirota multi-linear method; Swift-Hohenberg equation; direct ansatz method

文章编号:1674-232X(2015)06-0625-07

中图分类号:O175.4MSC2010: 39A20

文献标志码:A

doi:10.3969/j.issn.1674-232X.2015.06.012

通信作者：徐衍聪(1970—)，男，副教授，博士，主要从事微分方程与动力系统研究.E-mail：yancongx@163.com

基金项目：浙江省自然科学基金项目(LY13A010020);杭州师范大学科研基金项目(HNUEYT2013).

收稿日期：2015-01-25