横向流中细长圆柱的热弹性颤振*

李云东 杨翊仁

(1.西南交通大学力学与工程学院 成都 610031)(2.四川理工学院理学院，自贡 643000)

引言

管束振动是当流体流过换热器的管阵时，流体力、惯性力、和弹性力联合作用下动力失稳而发生的自激振动.动力失稳将引起管的毁坏，管大幅度的振动可能会引起管与管之间的碰撞以及管与折流板之间的磨损［1］.在一定流速下，如果流体给管子的能量大于管子阻力消耗的能量，管子的振幅突然增大，即发生了一般所说的流弹性振动.在流弹性失稳后，随着流速增加，结构运动的幅度增大，系统非线性影响变得重要.Weaver［2］指出非线性是换热器管阵结构的固有性质，主要来自于管与松散支撑 的 折 流 板 的 碰 撞.Paidoussis和Li［3］、Chen etal［4］、Cai和Chen［5］、de Bedout［6］、王琳［7］都研究过管阵中管子带有结构强非线性的横向流致振动，复杂的动力学行为可能出现，尤且是可能出现混沌运动.以上研究均未考虑热效应的影响，实际上换能器中的管阵，将经历严酷的热环境.

本文是在Paidoussis和Li［3］研究的基础上，继续考虑管的非线性响应问题.以圆柱阵中一根典型单柱为研究对象，首先建立了考虑热效应的圆柱的动力学方程，然后应用Galerkin方法离散运动方程，首先分析了热载荷对系统临界流速的影响，采用数值方法研究了随着横向流速的变化，系统出现的非线性动力学现象，包括混沌和周期窗口在内的各种复杂响应.

1 动力学方程

本文为了分析方便，把管当作圆柱来处理，横向流作用下的圆柱阵中，取一根弹性圆柱，其两端固支，中间受到折流板的约束的圆柱模型，如图1所示.圆柱排外部遭受横向流，流体速度和密度为U和ρ，圆柱直径为D，圆柱长度为l.

在模型中，考虑振动圆柱中间受到折流板的约束，模拟为圆柱中间作用有非线性弹簧，其弹簧约束考虑为立方非线性弹簧，弹簧约束力与圆柱振动位移关系为:

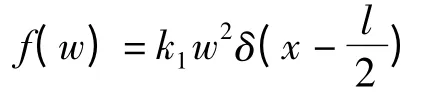
其中:k1为刚度，δ为Dirac delta函数

Mx是圆柱的弯矩;w为圆柱横向振动的变形;c是结构的黏性阻力系数;m是每单位长度圆柱质量;F是横向流作用在圆柱上的流体力.

圆柱横向位移导致圆柱轴向伸长而引起的附加力

其中:σ是应力，A是圆柱的横截面.

根据Wickert的弹性梁简化模型，应变位移关系为:

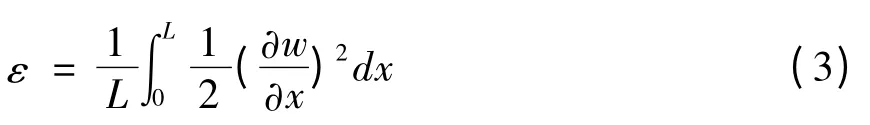
设材料为完全弹性材料，考虑温度的影响，有:

其中:E是弹性模量，αT是热膨胀系数，ΔT=TT0，T0:初始温度，T:升高温度.

把(3)代入(4)得到沿x轴变化的附加轴力为:

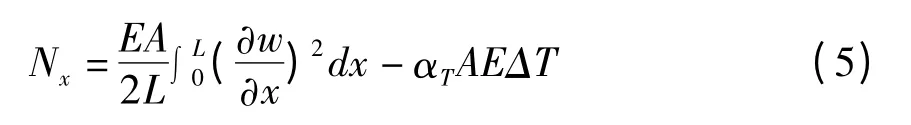
弯矩Mx:

其中:I截面惯性矩.

把(5)(6)代入(1)，有:

流体力F是圆柱运动位移函数，文献［3］［7］给出了“准稳态”模型来表示，Price和Paidoussis［8］展示了运用此模型的得到的管阵稳定性结果与实验数据具有较好的一致性.

图1 (a)横向流中的圆柱阵(b)中间约束的弹性圆柱Fig.1 (a)Array of cylinders in cross flow(b)A single elastic cylinder with intermediate constraints

其中:

CL和CD是圆柱阵中圆柱的升力和阻力系数，Cma是流体附加在圆柱上的附加质量系数，U是来流速度，D是圆柱直径，ρ是流体密度，Δt是时间延迟来自于圆柱运动和流体力之间的耦合作用时有滞后效应.

引入无量纲参数:

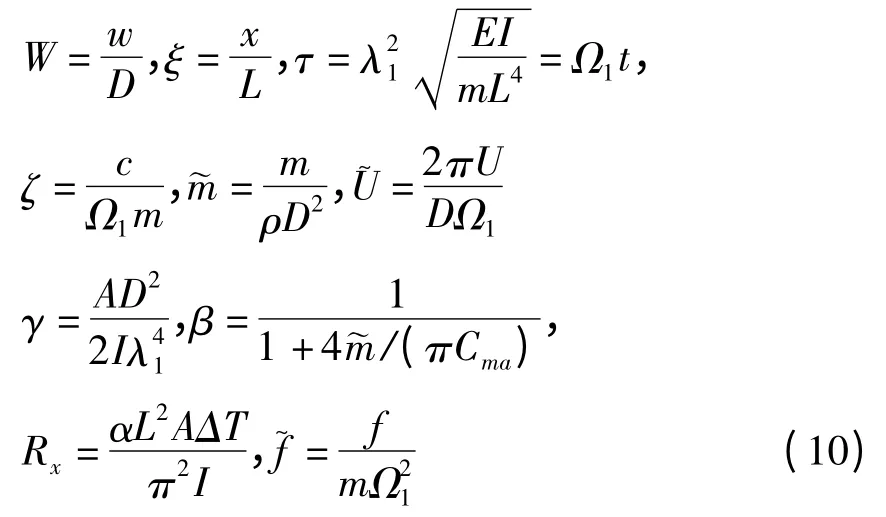
把无量纲量(10)代入方程(7)得到无量纲的运动方程为

2 运动方程离散

采用Galekin方法对方程(11)进行离散，满足固支边界条件的圆柱位移函数取为:

其中:

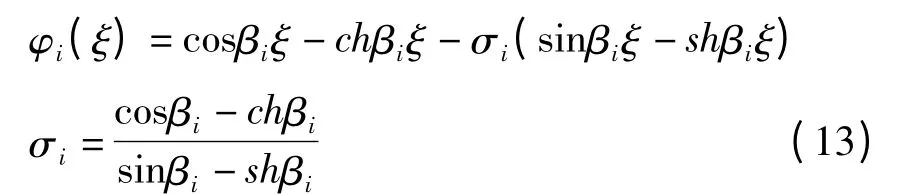
为固支梁的振型函数.

［9］，得固支梁的前五阶特征根为

由此算得:

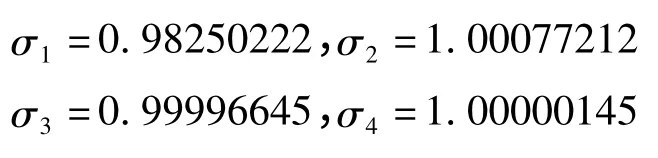
将式(12)代入方程(11)，利用振型函数的正交性，并在［0，1］区间内积分，可得微分方程:

式中

本文所用参数取值如下［2］:

3 线性系统稳定性分析

由式(17)方程的系数可以得到，对于方程(16)的线性部分奇数阶模态和偶数阶模态是解耦.一般地，系统首先是发生低阶模态失稳，为了方便计算，本文截取前1，3阶模态进行分析，由式(16)，且令

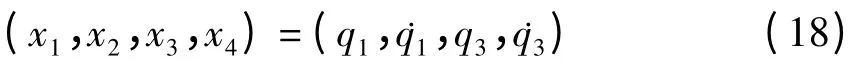
可得:

很显然式(19)有一个平衡点(0，0，0，0)，在平衡点附近，线性化方程(19)，得:

其中:

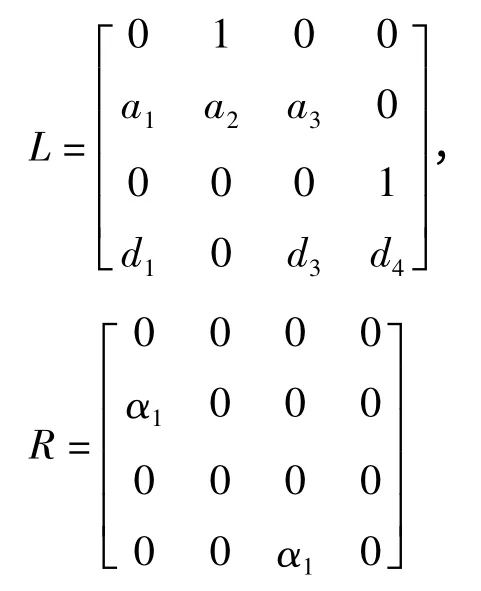
这里各参数为:

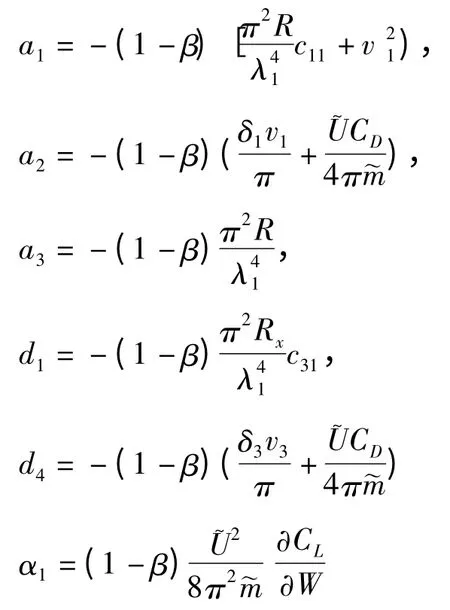
设方程(20)的解为

把上式代入(20)得，特征方程为:

设λ=σ+iω，当σ＜0时，平衡态是渐进稳定的，当σ＞0时，平衡态是不稳定的.当σ=0，系统的特征值有一对纯须根，一般地，这时候系统会出现颤振.把代入(22)，并且分离方程的实部和虚部，可以得到:

为虚部的方程.

为实部的方程.

通过求解方程(23)(24)，可以得到系统发生HOPF分岔的临界速度和对应的无量纲频率，如表1.接下来，作者将给出在不同热载荷作用下的临界速度.

表1 随温度升高无量纲临界速度和频率Table 1 Dimensionless critical velocity and frequency with increasing temperature

从表1可以看出，随着热载荷的增加，系统发生颤振的临界速度在不断降低.在实际工程应用中，管阵作为能量交换设备，我们应该考虑热环境的影响，系统实际发生失稳的临界速度应该比没有考虑热载荷计算出来的临界速度要小.

4 数值分析及结果

一般地，线性稳定性分析是用来预测参数值接近稳定边界的行为.然而无法预测参数值远离稳定性边界以后的系统响应情况.在这节里我们将采用数值算法，研究参数值远离稳定性边界后的动力学行为.采用龙格-库塔算法对运动控制常微分方程(16)进行计算，初始条件取为由方程(16)可以看到，在非线性项里，奇数阶模态和偶数阶模态不再解耦，所以我们取固支梁的前五阶模态进行数值计算.

取温度Rx=1，γ=300，k=104，采用分岔图和相图描述圆柱位置ξ=0.5处的响应.当位置在ξ=0.5处的响应到达稳态时，速度为零时，记录此时的位移，便得到了位移随流速变化的分岔图，如图2所示.从分岔图可以看出，系统经历了稳定状态，周期运动状态，拟周期运动状态，最后是周期1运动变为混沌运动.

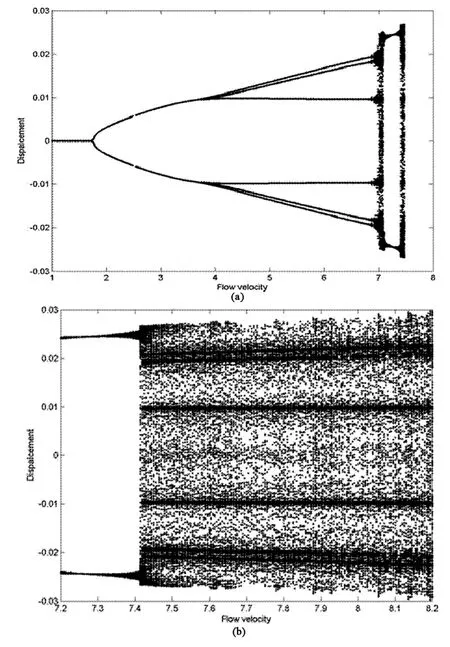
图2 ξ=0.5处流速参数区域分岔图(a)0≤U≤7.2(b)7.2≤U≤8.2Fig.2 Bifurcation diagram of the parameter of fluid speed atξ=0.5(a)0≤U≤7.2(b)7.2≤U≤8.2

从图2中看到，随着横向流速的不断增加，系统呈现非常复杂的非线性动力学现象.当流速U＜1.562时，系统呈现为稳态运动;当流速1.562＜U＜3.83时，系统发生极限环运动;流速在3.83＜U＜6.85时，系统呈现为周期3运动;流速在6.85＜U＜7.18时，系统发生短暂时的拟周期运动;流速在7.18＜U＜7.42时，系统又呈现极限环运动，当U＞7.42以后，系统出现混沌运动.

下面我们将以相图更加清楚地描述了系统的运动过程.图3(a)为U=1.9(U＞Ucr=1.562)时的情况，系统发生极限环振动.当U=5.5时，系统出现周期3运动(图(b))，时，系统发生拟周期运动，U=7.3时，出现周期1运动，U=8.0时，系统呈现混沌运动相图.

图3 各流速下系统的相轨迹图Fig.3 Phase portraits of system with various velocity

5 结论

本文考虑横向流圆柱阵中单弹性细长圆柱体，在定常温度下，圆柱的热弹性颤振问题.基于横向弯曲振动引起轴力变化的以及圆柱振动与折流板发生碰撞，建立了温度效应下弹性圆柱横向流致振动的动力学方程.研究了系统的分岔，并采用数值方法研究了系统的非线性响应，得到了一些结论:

(1)线性颤振分析得到了颤振临界度随温度变化的关系，温度升高降低了系统的稳定性.

(2)随着横向流速增加，系统经历了稳态运动和极限环运动、拟周期运动，然后再次发生周期运动，最后进入混沌运动.

参考文献

1 Paidoussis M P，Price SJ，Langre E de.Fluid structure interaction cross-flow-induced instability.New-York:Cambridgeuniversity press，First published，2011

2 Weaver D S，Fttzpatrick J A.A review of cross-flow induced vibrations in heat exchanger tubes arrays.Journal of Fluids and Structures，1988，2:73～93

3 Paidoussis M P，Li G X.Cross-flow induced chaotic vibrations of heat-exchanger tubes impacting on loose supports.Journal Sound of Vibration，1992，152:305～326

4 Chen S H，Chen S S.Chaotic vibration in fluid-stiffnesscontrolled instability of a tube row in crossflow.Journal of Applied Mechanics，1996，63:487～492

5 Cai Y，Chen S S.Chaotic vibration of nonlinear supported tubes in cross flow.Journal of Pressure Vessel Technology，1993，115:128～134

6 De Langer E，Hadj-sadok C，Beaufils B.Non-linear vibrations induced by fluidelastic forces in tube bundles.In proceedings International Symposium on Flow-induced Vibration of Cylinder Array.New York:ASME，1992:107～134

7 王琳.横向流引起含松动支撑细长圆柱体的失稳与非线性振动.第十二届全国非线性振动暨第九届全国非线性动力学和运动稳定性学术会议论文集.镇江:江苏大学出版社，2009(Wang L.Cross-flow-induced instability and non-linear vibrations of slender cylinder subjected to loose support.In:The Twelfth National nonlinear vibration＆the Ninth National Conference on nonlinear dynamics and stability of motion，Zhenjiang:Jiangshu University Press，2009(in Chinese))

8 Price SJ，Paidoussis M P.A single-flexible-cylinder analysis for the fluidelastic instability of an array of flexible cylinders in cross flow.Journal of Fluids Engineering，1986，108:193～199

9 倪振华.振动力学.西安:西安交通大学出版社，1989(Ni Z H.Mechanism of vibration.XiAn:Xian Jiaotong University Press，1989(in Chinese))