时变耦合神经振子集群刺激依赖性相响应同步*

盛祝梅 焦贤发

(合肥工业大学数学学院，合肥 230009)

引言

耦合神经元集群同步振荡活动是表达脑皮层内部及皮层之间信息通讯及信息整合的功能信号，例如视觉捆绑［1］、工作记忆［2］等.神经同步振荡活动除了在实现正常的脑功能中起了关键性作用外，与异常的神经疾患也有密切的联系，例如帕金森氏症、癫痫［3］等.神经同步振荡活动的产生与转迁的研究无论在电生理还是理论神经科学研究方面都是研究热点问题.根据单个神经元活动的电生理特性及皮层神经元执行认知任务时的同步振荡行为，将单个神经元模拟成神经振子、皮层神经元网络模拟成神经振子网络［4］，研究大脑皮层神经元集群活动的动力学机制.Kuramoto［5］和Tass［6］等在耦合神经振子群模型中将耦合参数设定为固定不变的常数，研究神经振子群的同步或非同步化行为.有些学者将噪声作为一种特殊的外部驱动力，或者考虑不同形式的噪声(白色噪声、乘性噪声)，来研究耦合神经振子群活动的动力学行为［7-12］.但他们在考虑外部干扰的时候，并没有考虑到大脑中神经元集群活动的自然特性，例如突触在分泌电化学神经递质时刺激相邻神经元放电，改变了相邻神经元间的连接程度，调节突触耦合强度［13，20-22］.长时程增强(long–term potentiation，LTP)是突触传递功能可塑性的重要表现形式，是研究学习与记忆的重要机制，同时也是影响长时程记忆(long–term memory，LTM)形成的重要因素之一［14］.在刺激作用下，LTP的形成影响神经元之间的耦合强度，从而影响神经元的突触学习效率.因此，考虑耦合强度的变化能够更加真实反应神经元集群活动的同步动力学行为.

相响应曲线(PRC)反映了重复放电的神经元受到外部刺激时，刺激如何影响峰电位的发放时间［15］，且被认为是研究神经系统同步活动动力学机制一个重要而有效的方法［16-18］.因此，本文基于神经元突触可塑性，研究耦合强度随时间变化，神经振子群刺激依赖性的同步振荡活动的动力学行为.

1 数学模型

考虑外部刺激作用下，N个全局耦合神经振子组成的神经元振子群的随机演化模型［7、19］.

其中i=1，2，…，N，N＞1.θi和θj分别为神经振子i和j的相位，w是神经元振子的自然频率，F(t)是外部谐波刺激，本文取F(t)=I sin(ct)，I是刺激强度，c是刺激频率，sinθi是相位敏感函数.K表示神经振子之间的突触耦合强度，Ken、Eward等在模型研究中将耦合强度设定为固定不变的常数［7、19］.然而，大脑皮层神经网络在信息处理过程中神经元之间的耦合强度是不断变化的，因此我们假设耦合强度的时间演化模型为

τ为耦合强度的衰减常数，D为学习效果，t1，t2，…，tk为突触前神经元峰电位周期发放时间序列.

为了研究神经振子集群的同步振荡活动，我们引入描述神经振子集群活动的序参数

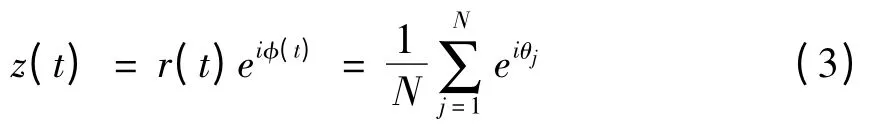
r(t)和φ(t)分别表示随时间变化的平均场幅值和平均场相位，r(t)描述神经振子群的同步化强度，0≤r(t)≤1，r(t)越大表明同步化程度越强;当神经振子的相位均相同，即神经振子群完全相位同步时，r(t)=1;当神经振子处完全不相干活动时，r(t)=0.

当组成神经振子集群的振子数N充分大时，可用概率密度函数f(w，θ，t)描述神经振子集群的状态，即t时刻振子相位和自然频率分别落入区间［θ，θ+dθ］、［w，w+dw］的概率为f(w，θ，t)dθdw.于是，描述神经振子群整体活动行为的序参数可表示为

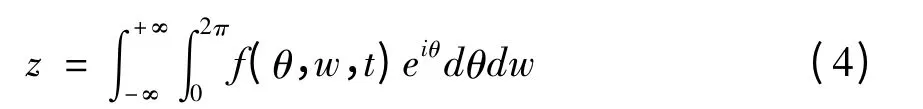
f的演化方程为［8］:

v(w，θ，t)是N→∞时对应方程(1)在圆周上的速度场，

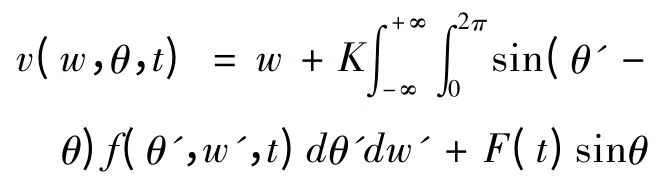
由于

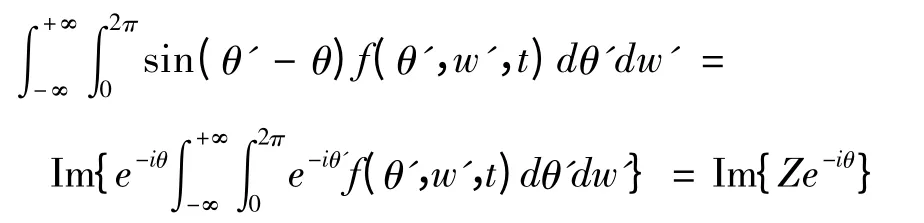
其中 表示复数的虚数部分.由此，(5)式可转化为

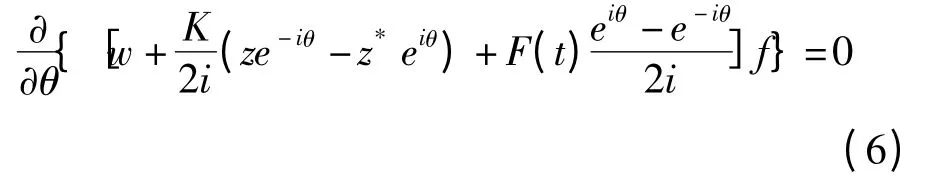
为解方程(6)，利用Ott-Antonsen假设［19］:

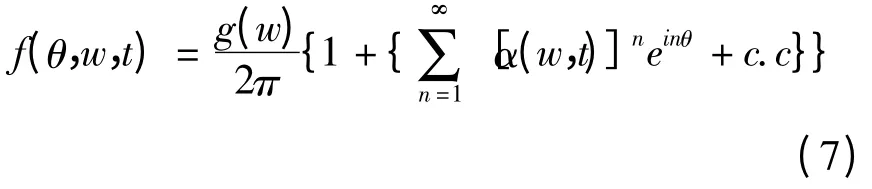
c.c表示共轭部分，将上式代入(4)式，得到

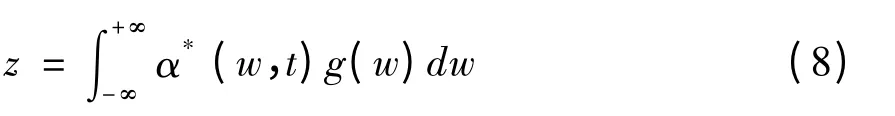
将(7)、(8)式代入方程(6)，得到关于α(w，t)的演化方程

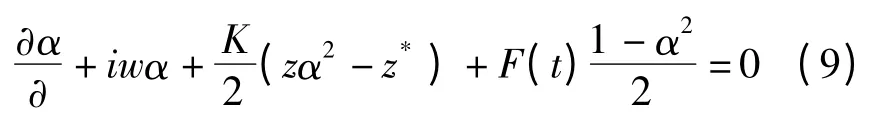
将z(t)=r(t)eiφ(t)代入方程(10)，进一步得到关于序参数的幅值r(t)和相位φ(t)的演化方程:

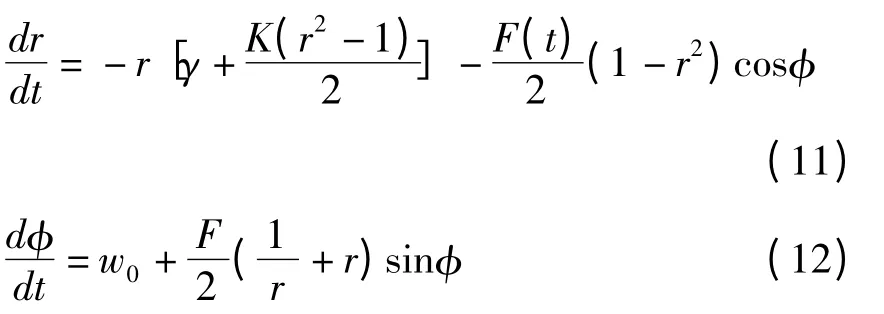
2 数值分析

图1表明神经振子之间时变耦合的突触学习效果.在没有突触输入的情况下(D=0)，突触耦合强度随时间的演化渐渐趋向于零;当接受突前神经元峰电位输入时，突前神经元神经发放时间序列取为周期发放时间序列，通过数值分析我们发现突触耦合强度明显加强.

为了研究刺激对神经振子集群活动的影响，本文考虑相同的初始条件下，不同的刺激强度和刺激频率对神经振子集群同步活动的影响.内部参数设定为γ=0.1，w0=1.5，τ=0.005，用四阶龙格-库塔法求出方程(11)、(12)的数值解.

图2呈现出在不同刺激频率条件下序参数的幅值随时间的演化.在适当强度的刺激下，低频刺激会使神经振子集群产生完全相位同步行为.然而，随着刺激频率的增加，神经振子集群进入同步周期振荡活动.高频刺激可神经振子集群进入高频同步振荡，并且同步程度也越高.这表明神经振子群对高频刺激具有快速的响应能力，刺激频率是由神经振子群的同步振荡活动的频率编码.

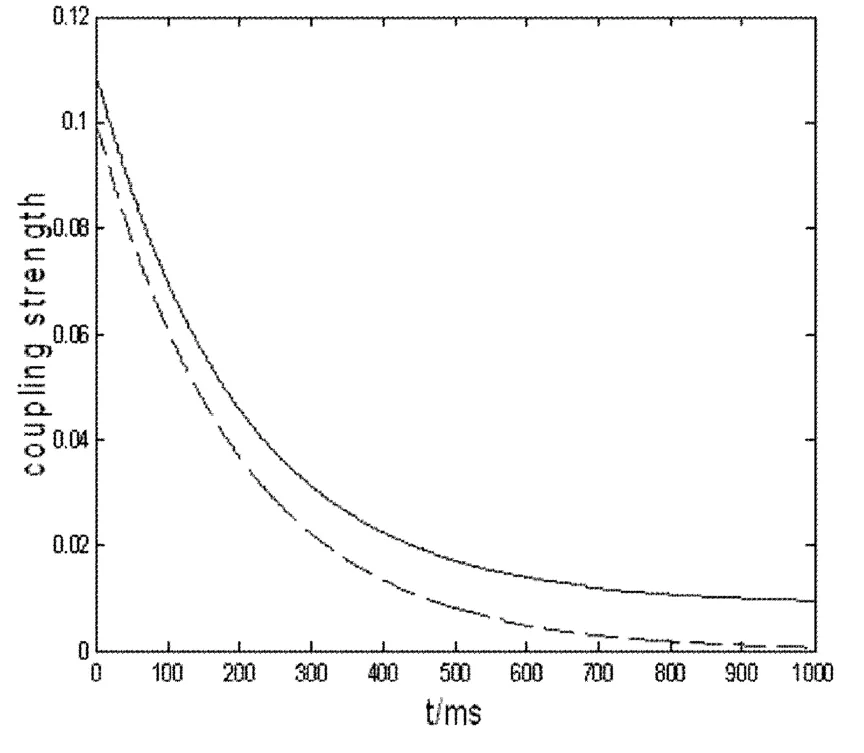
图1 神经振子之间的耦合强度随时间演化参数:τ=0.005，D=0(虚线)，D=0.001(实线)Fig.1 The evolution of coupling strength between neuronal oscillators with respect to time.Parameters:τ=0.005，D=0(dashed line)，D=0.001(solid line)

图2 在不同刺激频率条件下，序参数幅值随时间演化参数:I=5，γ=0.1，w0=1.5，τ=0.005，D=0.001Fig.2 The evolution of the amplitude of the order parameter with respect to time in the presence of stimulation with different frequency.Parameters:I=5，γ=0.1，w0=1.5，τ=0.005，D=0.001

图3呈现了在不同刺激强度及刺激条件下，序参数的幅值随时间的演化.在低频弱刺激下，神经振子群的相位同步响应比较弱;但随着刺激强度的增加，神经元振子群进入完全相位同步活动状态，并且强刺激会使神经元振子群更快速进入相位同步活动(图3(a))，这表明在弱频刺激下，刺激强度可由神经振子集群进入完全相位同步活动的响应时间编码.在高频刺激下，弱刺激只能使神经振子群产生微弱的同步周期振荡;但随着刺激强度的增加，相位同步周期振荡活动更明显，刺激越强同步程度越大，而振荡的频率不随刺激强度的同步而改变(图3(b))，这表明在高频刺激下刺激强度由相位同步程度编码.

图3 在不同刺激强度条件下，序参数幅值随时间的演化参数:γ=0.1，w0=1.5，τ=0.005，D=0.001;(a)c=0.01，(b)c=0.1Fig.3 The evolution of the order parameter with respect to time in the presence of stimulation with different intensity.Parameters:γ=0.1，w0=1.5，τ=0.005，D=0.001;(a)c=0.01，(b)c=0.1

3 小结

Ken等研究了噪声导致的耦合振子群的相位同步，同步转迁依赖于噪声强度，噪声越大会导致同步转迁的耦合强度的阈值变小［7］.与Ken等研究工作不同，本文考虑到耦合强度的变化，利用神经振子相位响应曲线建立神经振子集群在外刺激作用情况下的相位响应动力学模型，此模型更加真实反应神经元集群活动的同步动力学行为.数值分析结果表明外刺激对神经振子群同步活动的影响依赖于刺激强度和刺激频率.神经振子群对低频弱刺激的响应十分微弱;然而，随着刺激的增加，神经振子集群以近完全相位同步的方式对刺激作出响应，刺激越强响应时间越快.高频刺激能够使神经振子群产生同步振荡行为，刺激强度决定了同步程度，刺激越强同步程度越高;刺激频率决定了同步振荡的频率，刺激频率越高同步振荡频率也越高.刺激频率信息是由神经振子群的同步振荡活动的频率编码，刺激强度信息由相位同步程度编码.

1 Sompolinsky H，Golomb D，Kleinfeld D.Cooperative dynamics in visual processing.Physical Review A，1991，43:6990～7011

2 Wolfgang K.Memory processes，brain oscillations and EEG synchronization. International Journal Psychohysiology，1996，24:61～100

3 Lehnertz K.Non-linear time series analysis of intracranial EEG recordings in patients with epilepsy an overview.International Journal Psychophysiology，1999，34:45～52

4 Jiao X F，Wang R B.Synchronization in neuronal popuatlion with the variable coupling strength in the presence of external stimulus.Applied Physics Letters，2006，88:203901

5 Kuramoto Y.Collective synchronization of pulse-coupled oscillators and excitable units.Physica D，1991，50:15～30

6 Peter T.Resetting biological oscillators a stochastic approach.Journal of Biological Physics，1996，22:27～64

7 Ken H N，Hiroshi K.Noised-induced synchronization of a large population of globally coupled nonidentical oscillators.Physical Review E，2010，81:065202

8 Lauren M C，Steven H S.Stability diagram for the forced kuramoto modle.Chaos，18:043128

9 Bidhan C B.Influence of noise on the synchronization of the stochastic Kuramoto model.Physical Review E，2007，76:056210

10 Jiao X F，Wang R B.Synchronous firing patterns of neuronal population with excitatory and inhibitory connections.International Journal of Non-Linear Mechanics，2010，45:647～651

11 Arne W，Thomas M，and Jens C C.The phase response of the cortical slow oscillation.Cognitive Neurodynamics，2012，6:367～375

12 王青云，陆启韶.兴奋性化学突触耦合的神经元同步，动力学与控制学报，2008，6(1):35～39(Wang Q Y，Lu QS.Synchronization of coupled neurons excitory chemical synapse.Journal of Dynamics and Control，2008，6(1):35～39(in Chinese))

13 Cumin D，Unsworth CP.Generalising the Kuramoto model for the study of neuronal synchronization in the brain.Physica D，2007，226:181～196

14 韩太真，突触可塑性与长时程增强现象的研究进展.西安交通大学学报(医学版)，2005，26:305～315(Han T Z.Progress in research of synaptic plasticity and longterm potentiation.Journal of Xi’an Jiaotong University(Medical Sciences)，2005，26:305～315(in Chinese))

15 Boris S G，Ermentrout G B.Alex D R.Phase-response curves give the responses of neurons to transient inputs.Journal of Neurophysiology，2005，94:1623～1635

16 Roy M S，Ermentrout G B，John A.W.Phase-response curves and synchronized neural networks.Philosophical Transaction of the Royal Society B，2010，365:2407～2422

17 Roberto F G，Bard Ermentrout G，Nathaniel N U，Efficient estimation of phase-resetting curves in real neurons and its significance for neural-network modeling.Physical Review Letters，2005，94:158101

18 Yasuhiro T，Masahiko T，et al.Layer and frequency dependencies of phase response properties of pyramidal neurons in rat motor cortex.European Journal of Neuroscience，2007，25:3429～3441

19 Eward O，Thomas M A.Low dimensional behavior of large systems of globally coupled oscillators.Chaos，2008，18:037113

20 Petkoski S，Stefanovska A.Kuramoto model with timevarying parameters.Physical Review E，2012，86:046212

21 Cooke S F，Bliss T V P.Plasticity in the human central nervous system.Brain，2006，129:1659～1673

22 Yuri M，Borys L，et al.Multistability in the Kuramoto model with synaptic plasticity.Physical Review E，2007，75:066207