关于HTR球床堆叠密度统计方法的研究及应用

于福江，谢 菲，孙喜明（清华大学核能与新能源技术研究院，先进核能技术协同创新中心，先进反应堆工程与安全教育部重点实验室，北京 100084）

关于HTR球床堆叠密度统计方法的研究及应用

于福江，谢 菲，孙喜明＊
（清华大学核能与新能源技术研究院，先进核能技术协同创新中心，先进反应堆工程与安全教育部重点实验室，北京 100084）

摘要：球床式高温气冷堆是目前中国自主研发的主要堆型，对于球床内的球体随机堆叠密度分布的统计分析是高温气冷堆物理－热工计算和安全分析的重要问题之一。针对这一问题，提出了一种新的堆叠密度分布的统计方法。通过与传统格子填充法计算结构和实验值进行对比，验证了该方法的高效性和准确性，同时帮助传统格子填充法找出最佳的单元尺度，并尝试利用该方法对实验中多次观察到的边界效应进行分析。

关键词：高温气冷堆；堆叠密度；格子填充法

球体随机堆叠密度对于球床式高温气冷堆（HTR）［1－3］有着重要意义，反应堆物理－热工计算及安全分析均依赖于对堆芯内部球体随机堆叠密度的准确统计。球体随机堆叠密度［4－5］的分析是高温气冷堆研究的难题之一。由于高温气冷堆球床的燃料球处于随机堆叠状态，对其堆叠密度分布进行实验测量十分困难，且越靠近球床中心，往往误差越大。因此，数值模拟就成为对大量球体随机堆叠进行分析的主要方法。

目前，针对堆芯球床内燃料球分布的计算方法已有许多相关的研究，Chris等［4］和Heikki等［5］的研究表明，堆芯内的堆叠密度对于反应堆中子通量和热工方面的研究有着重要意义。一些关于堆叠对加速器驱动次临界系统（ADS）堆型的影响可在Garcíaa等［6］的工作中找到，关于超高温气冷堆（VHTR）中堆叠密度与传热系数的关系的相关研究由Abdulmohsina等［7］在其工作中给出，另外还有一些研究［8］分析堆叠密度与强制对流特性的关系。鉴于堆叠密度对反应堆计算分析的重要性，针对于该问题已有许多相关的实验探究。在van Antwerpena等［9］和de Klerk［10］的研究中总结了大量关于底部和近壁面附近空隙率变化的测量。针对HTR－10，Yang等［11－12］也给出了其堆叠密度的实验和数值分析。

目前对于球体随机堆叠问题的数值模拟，主要采用离散单元法（DEM）［13－14］，现已有一些研究实现其在球床堆内堆叠问题的动态计算［15］和加速计算［16］。然而DEM仅能提供压力容器内燃料球球心的分布数据，无法直接得出对工程有实际意义的堆叠密度，故而对DEM结果的再处理势在必行。如何高效、准确地计算并分析堆叠密度仍是一有待解决的问题。传统的手段是利用立方体单元逼近球体填充区域（简称“格子填充法”），本工作将利用数值积分法来实现这一任务，同时通过对格子填充法和数值积分法的对比，验证数值积分法的可行性与准确性，找出传统格子填充法对于工程计算最有意义的格子尺度，并通过对高温气冷堆压力容器近边界附近的堆叠密度的分析，给出广泛存在的有限单元堆叠边界效应合理的解释。

1　堆叠密度的统计方法

1．1 格子填充法

格子填充法源于早期的3D图形渲染技术，即利用一定数量的单元格子可逼近整个3D曲面。通过对3D几何体填充的格子总数的统计，可得出其体积的近似结果。

对于HTR的整体圆柱状堆芯，以间距h分别从径向和轴向对其进行分割，从而得到一个个高度和厚度均为h的圆环柱体，再将圆环柱体外壁以h为间距分割成一个个小单元，这样的单元即为所需要的单元格子，如图1所示。

对于实现格子填充法，有两种不同的实现算法：第1种是基于球体的统计方式，第2种是基于格子的统计方式。前者将遍历每个球体，并根据球心位置查找周围与其相交的格子总数。根据这一方式，逐一分析所有球体。如图2a所示，灰色格子是与某个球体相交的格子。后者对于基于格子的统计方式，将尝试固定每个格子，并根据格子的位置来确定周围是否有与其相交的球体。对于判定格子与球体是否相交，可采用格子的中心点作为参考，如果格子中心点在球体内部，则认为格子被球体填充，如图2b所示。对于格子的填充状态，可利用下式加以确定：

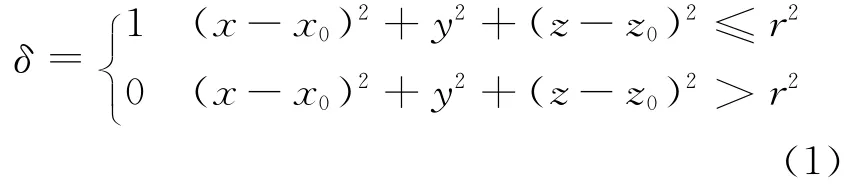
其中：x0为燃料球球心与轴线的轴向距离；z0为燃料球球心与底面的轴向距离；x、y、z为给定格子的取样点坐标。δ＝1代表格子被填充，δ＝0代表格子未被填充。

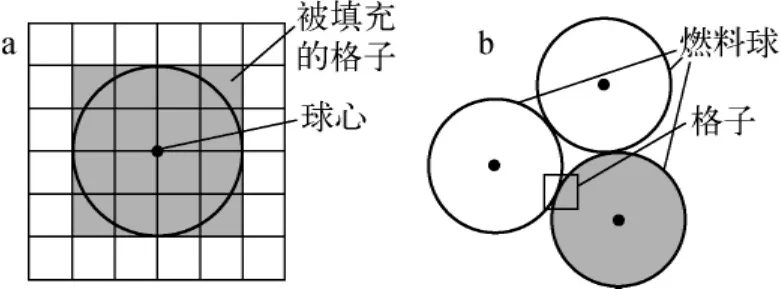
图2 基于球体（a）和格子（b）的方式Fig．2 Sphere－based（a）and lattice－based（b）ways

基于球体的统计方式，其优点是实现过程较为简单，而且整个过程只需将所有球体循环分析1次，即可完成整体的堆叠密度分析，但在整个计算过程中，为防止重复填充现象发生，必须保存所有格子的填充状态，从而带来更多的内存消耗。而基于格子的统计方式，其优点是对格子进行1次性遍历，但存在大量的重复计算。本文采用基于球体的方式来实现格子填充法。

1．2 数值积分法

格子填充法往往并不能得出高精度的结果，尤其在格子尺度不够小的情况下。由于格子尺度的缩小意味着格子数量的增加，这会带来计算量呈3次方增长，巨大的内存和CPU消耗是该方法的一显著问题。

相较于利用格子填充的近似逼近思想，利用数值积分法更易实现对堆叠密度的精确分析。在数值积分法中，将不再需要对图1中划分的单元环柱进一步分割为格子，因为单元环柱本身就是该方法的基本单元，从而大幅简化单元结构、缩小储存量。同时，燃料球与给定单元的相交体积将被精确计算，如图3所示。

欲精确计算燃料球与给定单元的相交体积，需给出相交体积的三重积分表达式。为提高计算精度，需推导三重积分表达式中的径向截面积分，从而使计算体积的三重积分转化为针对轴向高度的定积分。对于该积分表达式的形式，存在4种基函数，对应于不同相交状况的表达式可认为是上述4种基函数定积分的叠加。各基函数的表达式如下：

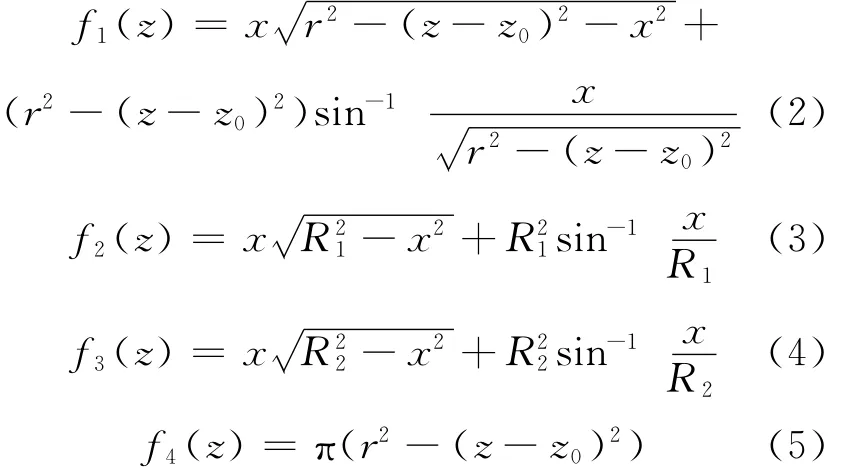
其中：z为被积函数中的变量；x为一个由球心与单元位置关系决定的变量，可通过具体的相交情况进一步确定；R1、R2分别为给定圆环的内半径和外半径；r为燃料球半径；z0为球心轴向坐标。

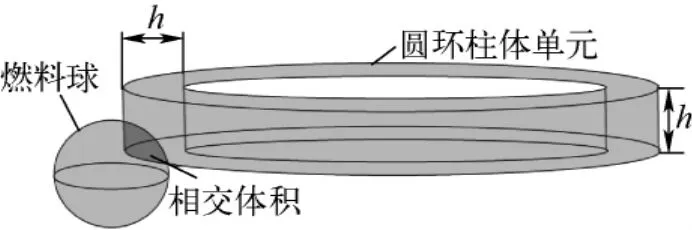
图3 应用数值积分法统计的堆叠体积Fig．3 Packing volume calculated by numerical integral method

具体的计算过程描述如下：

1）对于不同的相交情况，首先需分析燃料球与圆环单元的径向及轴向位置关系，从而确定该相交情况所需的基函数；

2）依照径向位置关系，将基函数表达式中的x代换为具体数值，并将其叠加得出体积定积分中被积函数的表达式；

3）通过燃料球与圆环单元的轴向位置关系确定积分上下限，并通过数值积分方法，如辛普森积分，完成积分计算。

现以图4中的相交模型为例，展示数值积分法的一般步骤。

首先，根据圆环与燃料球的相交情况，将其积分表达式分为za－zb、zb－zc、zc－zd3段。其中，za－zb段与zc－zd段类似，可用同一函数表达。

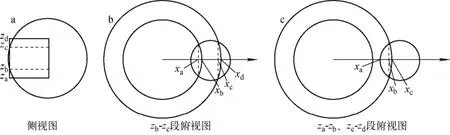
图4　 数值积分法应用举例Fig．4 Example for numerical integral method

根据分析可得，图4a中各参数表达式为：

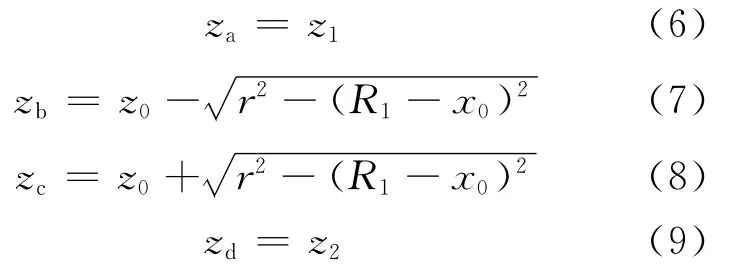
其中，z1、z2分别为圆环柱上、下底面与底面的轴向距离。

对于图4b中的参数，通过分析，可确定其表达式为：

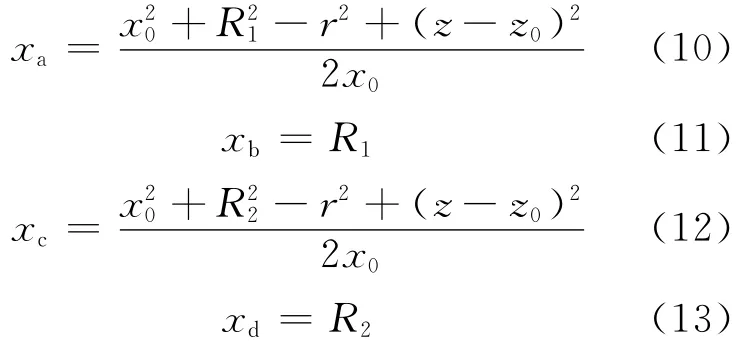
对于图4c中的参数，通过分析，可确定其表达式为：

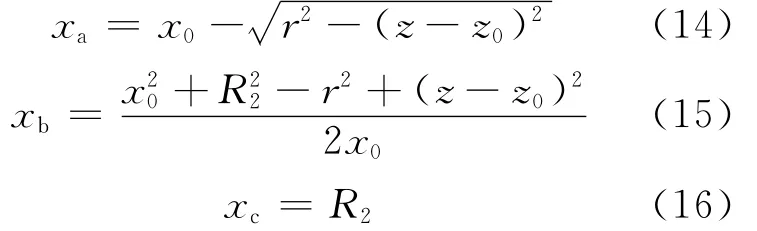
从而，各段体积的表达式为：

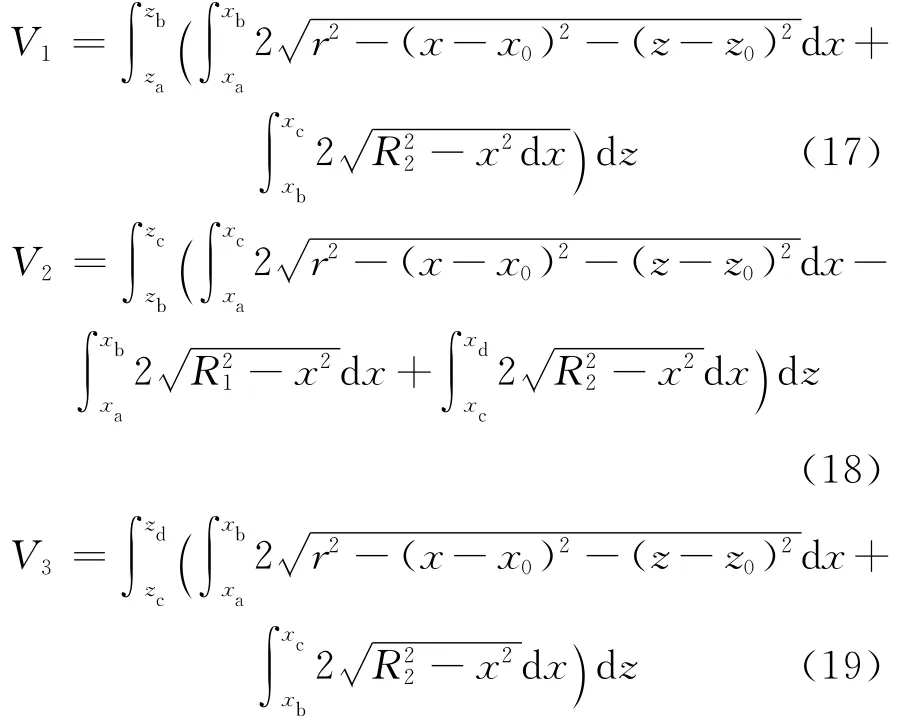
通过对体积积分表达式进行符号运算并化简，可发现其表达式可分解为4种与z相关的函数，亦即上文提到的4种基函数。因而，上述体积积分表达式最终可化简为：

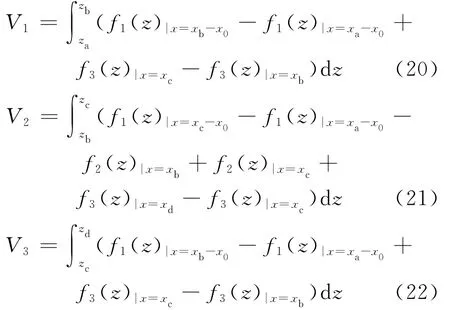
上述表达式已无法再通过符号积分的方式进行化简求解，故而利用辛普森数值积分的方式对其求解，并将V1、V2、V3累加，即可得出该燃料球在选定圆环柱单元中的堆叠体积。

由上述分析，可看出数值积分法的实现过程需要冗长的数学公式推导。与此同时，由于燃料球与单元的相对位置关系复杂，分别讨论各相交模型对应的体积积分表达式亦颇为繁琐，图5仅示出了大量相交情况中的一部分。在不同的相交情况下，积分的上、下限与表达函数均存在差异。虽然数值积分法的实现过程颇为繁琐，但数值积分法能大幅削减计算量，并得出更为精确的结果。

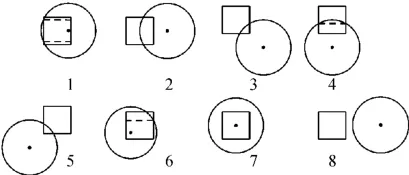
图5　 球体与单元的相交情况Fig．5 Different intersected conditionsfor sphere and element

2　利用数值积分法分析球床堆堆叠密度

2．1 数值实验参数

为检验数值积分法的效果，应用该方法对HTR－10堆芯球床进行球体随机堆叠密度统计分析。HTR－10的相关参数［17］列于表1。图6 为HTR－10堆芯的几何形状参数。

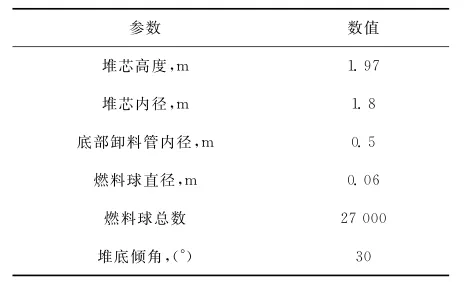
表1　 HTR－10的相关参数Table 1 Parameter of HTR－10

球床内球体随机堆叠的数据由带重力动态加载的DEM（DPPM）计算得到［18］，为避开球床上下边界的影响，选取z＝1．6～1．66m之间的区域进行分析。分别将该区域沿径向以间距h＝d／6、d／3、d／2、1d进行分割，并分析堆叠密度沿径向的变化。其中，d为球体直径。

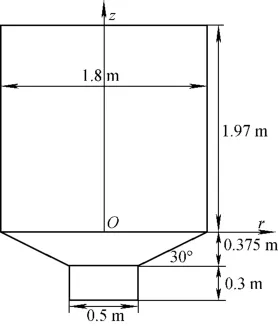
图6　 HTR－10堆芯的几何形状参数Fig．6 Geometric parameter of HTR－10

2．2 数值实验结果

根据以上参数，利用数值积分法和格子填充法对堆芯径向堆叠密度分布进行分析，并与实验测量结果进行对比。实验测量结果来自于德国模块堆HTR－MODUL［19］。图7为统计结果。

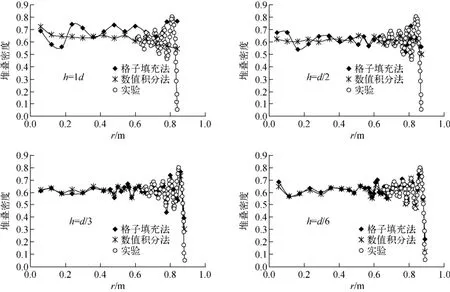
图7　 统计结果Fig．7 Statistic result

2．3 结果分析

从图7可看出，数值积分法与格子填充法能与实验契合，其中h＝d／6时，几乎与实验值完全符合。但h较大时，数值积分法仍能给出对应间距内实验值的平均结果，而格子填充法在单元间距小于d／3时已不再适用，单元间距的扩大大幅削弱了格子逼近过程的精度。同时数值积分法能更为准确地描绘堆叠密度沿径向的分布，而格子填充法则相对有更大的波动。

由图7还可看出，随h的减小，即网格尺度的缩小，堆芯内球体堆叠密度的分布在径向上的波动变得越来越明显。h＝1d时，几乎捕捉不到任何波动，径向分布的波动完全被淹没。而h缩小为d／2、d／3后，波动逐渐变得越来越明显。h＝d／6时，格子填充法可精确匹配实验值，包括在实验中测量到的壁面附近堆叠密度震荡现象。

为更精确地契合实验结果，推荐格子填充法选取d／6作为单元间距，而数据积分法采取d／3作为单元间距。同时，更小的单元间距将会带来更高精度的结果，但也会消耗更多的内存和CPU。

3　利用数值积分法分析离散单元填充中的边界效应

3．1 数值实验

在有限体积离散单元填充问题中，常常可在边界附近观察到堆叠密度的大幅震荡现象，目前的一些实验与数值研究［19－21］均已证明了这一点。本节将利用上述的格子填充法来捕捉壁面附近的边界效应，并给出其对应的理论解释。

数值实验的数据仍采用由DEM针对1．97m高温气冷堆所生成的燃料球球心分布数据。为尝试分析边界对堆叠密度所产生的影响，将分别针对底角为0°、15°、30°、45°和60°的情况，在高度z＝d／2处进行分析，其他相关设计参数均与表1提供的数据相同。本次圆环柱体单元所采用的间距将采取单元间距h＝d／6，并利用数值积分法对其进行分析。图8为不同底角的堆叠密度分布。由图8可看出，在5种不同底角的压力容器中，15°、30°、45°和60°情况下，堆叠密度分布极为相似，而底角为0°的情况下，其堆叠密度分布在0．25～0．9m之间则显得大为不同。

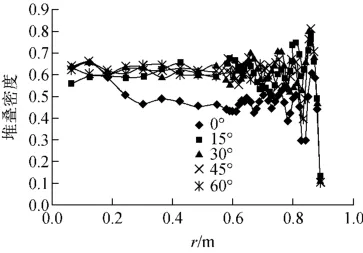
图8　 不同底角的堆叠密度分布Fig．8 Packing density distribution with different bottom angles

3．2 边界效应分析

边界效应的产生主要归因于边界附近空间的局限性与堆叠单元体体积的有限性。基于这两点因素，在有限体积单元堆叠问题中，常会在壁面附近产生堆叠密度的大幅震荡。

在单元体堆叠较为紧密的情况下，靠近壁面附近的空间会变得极为狭小，而有限单元体不能像连续介质一样在任意大小空间填充，因而在边界附近会产生一部分无法被堆叠的空隙，这对应于近边界堆叠密度震荡中的波谷。与此同时，由于边界的存在，在近边界的一层，有限单元体的堆叠会变得更加规律，而这对应于近边界堆叠密度震荡中的波峰。对边界效应的几何解释示于图9。

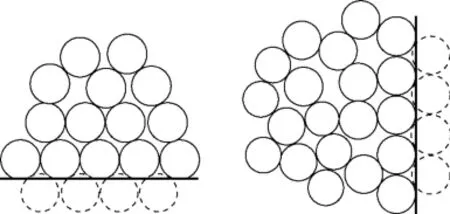
图9　 对边界效应的几何解释Fig．9 Geometric explanation for wall boundary effect

在壁面附近的有限单元体堆叠过程中，边界效应的空隙作用与规律作用交替出现，从而产生壁面附近的大幅震荡。而随堆叠向芯部的延伸，分布将变得越来越不规律，故而震荡沿径向逐渐减弱。

这种边界效应可用来解释底角为0°时的堆叠密度与15°、30°、45°和60°时所产生的差异。由于底角为0°时，压力容器底面对堆叠分布产生了截断作用，故而形成边界效应，在0°底角分布中表现为相对较低的堆叠密度。而由于在0～0．25m之间压力容器下部所存在的排泄管打破了压力容器底面对堆叠的截断，故而边界效应消除，5种不同底角下的分布趋于相同。

这种边界效应所造成的影响在图7中也有所体现。

4　结论

本文介绍了新的堆叠密度统计方法——数值积分法的原理及特性，并分析了其优缺点。通过计算高温气冷堆球床堆叠问题，在与实验结果的比照下，验证了数值积分法的准确性和高效性，并为格子填充法找出了最佳单元间距。同时，通过对球床堆底部堆叠密度的计算，尝试解释了离散单元堆叠问题中的边界效应。根据以上分析，可得出如下结论。

1）数值积分法可用来分析离散单元体堆叠问题，同时相较于传统的格子填充法，其精度更高，单元间距更大，而计算量需求更小。但相对而言，所需要的数学分析更为复杂。

2）通过与实验对比，得出格子填充法的最佳单元间距，亦即格子尺度，为d／6。同时，随格子尺度的减小，其结果更为精确，壁面附近的波动更为明显。

3）边界对于有限单元体堆叠问题存在正、负两种效应。在两种效应的作用下，近壁面往往可捕捉到堆叠密度的大幅振荡，而这种振荡随着向芯部的延伸而逐渐减弱。在有限单元体堆叠问题，例如球床燃料球堆叠，边界效应应予以考虑与重视，其对于堆芯安全可能造成一定影响。

参考文献：

［1］ 吴宗鑫，张作义．先进核能系统和高温气冷堆［M］．北京：清华大学出版社，2004．

［2］ 吴宗鑫，张作义．世界核电发展趋势与高温气冷堆［J］．核科学与工程，2000，20（3）：211－219．WU Zongxin，ZHANG Zuoyi．World development of nuclear power system and high temperature gas－cooled reactor［J］．Chinese Journal of Nuclear Science and Engineering，2000，20（3）：211－219（in Chinese）．

［3］ 刘俊杰，王敏稚，张征明，等．10MW高温气冷实验堆的堆体结构特点［J］．核动力工程，2001，22（1）：53－56．LIU Junjie，WANG Minzhi，ZHANG Zhengming，et al．Features of reactor structure design for 10 MW High Temperature Gas－cooled Reactor［J］．Nuclear Power Engineering，2001，22（1）：53－56（in Chinese）．

［4］ CHRIS H R，GARY S G，JAMES W L，et al．Analysis of granular flow in a pebble－bed nuclear reactor［J］．Phys Rev E，2006，74：021306．

［5］ HEIKKI S，JOUNI R，PAYMAN J，et al．Methods for modeling the packing of fuel elements in pebble bed reactors［J］．Nuclear Engineering and Design，2014，273：24－32．

［6］ GARCÍAA L，PÉREZA J，GARCÍAA C，et al．Calculation of the packing fraction in a pebble－bed ADS and redesigning of the transmutation advanced device for sustainable energy applications（TADSEA）［J］．Nuclear Engineering and Design，2012，253：142－152．

［7］ ABDULMOHSINA R S，AL－DAHHAN M H．Characteristics of convective heat transport in a packed pebble－bed reactor［J］．Nuclear Engineering and Design，2015，284：143－152．

［8］ BU S S，YANG J，ZHOU M，et al．On contact point modifications for forced convective heat transfer analysis in a structured packed bed of spheres［J］．Nuclear Engineering and Design，2014，270：21－33．

［9］ van ANTWERPENA W，du TOITB CG，ROUSSEAU P G．A review of correlations to model the packing structure and effective thermal conductivity in packed beds of mono－sized spherical particles［J］．Nuclear Engineering and Design，2010，240：1 803－1 818．

［10］de KLERK A．Voidage variation in packed beds at small column to particle diameter ratio［J］．AIChE Journal，2003，49：2 022－2 029．

［11］YANG X T，HU W P，JIANG S Y，et al．Mechanism analysis of quasi－static dense pebble flow in pebble bed reactor using phenomenological approach［J］．Nuclear Engineering and De－sign，2012，250：247－259．

［12］YANG Xingtuan，GUI Nan，TU Jiyuan，et al．3DDEM simulation and analysis of void fraction distribution in a pebble bed high temperature reactor［J］．Nuclear Engineering and Design，2014，270：404－411．

［13］KLOOSTERMAN J L，OUGOUAG A M．Spatial effects in dancoff factor calculations for PEBBLE－BED HTRs［C］∥Mathematics and Computation，Supercomputing，Reactor Physics and Nuclear and Biological Applications．Avignon，France：［s．n．］，2005．

［14］LI Yanheng，JI Wei．A collective dynamics－based method for initial pebble packing in pebble flow simulations［C］∥Proceedings of International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering（M＆C 2011）．［S．l．］：［s．n．］，2011．

［15］LI Yanheng，JI Wei．A collective dynamics－based method for initial pebble packing in pebble flow simulations［J］．Nuclear Engineering and Design， 2012，250：229－236．

［16］LI Yanheng，JI Wei．Acceleration of coupled granular flow and fluid flow simulations in pebble bed energy systems［J］．Nuclear Engineering and Design，2013，258：275－283．

［17］WU Z X，LIN D C，ZHONG D X．The design features of the HTR－10［J］．Nuclear Engineering and Design，2002，218：25－32．

［18］MUNJIZA A．The combined finite－discrete element method［M］．Hoboken：Wiley，2004．

［19］JAVIER B A．Estudio de lechos fluidizados de esferas aplicados a reactores nucleares HTR［M］．Spain：Universidad de Zaragoza，2011．

［20］HEIKKI S，JOUNI R，PAYMAN J，et al．Discrete element modeling of pebble packing in pebble bed reactors［J］．Nuclear Engineering and Design，2014，273：24－32．

［21］JOSHUA J C．Pebble bed pebble motion：Simulation and applications［C］．USA：Idaho State University，2010．

Research and Application of Packing Density for Pebble Bed in HTR

YU Fu－jiang，XIE Fei，SUN Xi－ming＊
（Institute of Nuclear and New Energy Technology，Collaborative Innovation Center
of Advanced Nuclear Energy Technology，Key Laboratory of Advanced Reactor Engineering and Safety of Ministry of Education，Tsinghua University，Beijing100084，China）

Abstract：The pebble bed high temperature gas－cooled reactor is one of the major types of reactors developed by Chinese nuclear technology．The statistical analysis for packing density in the pebble bed is an important issue of physical－thermal calculation and safety analysis．Aimed to this problem，a new kind of method was set up to solve this problem．Compared with the traditional lattice－fill method and the experiment，its efficiency and accuracy were verified，while helping to find out the best length of unit in the traditional lattice－fill method．This method was used to analyze the boundary effects observed by experiments．

Key words：high temperature gas－cooled reactor；packing density；lattice－fill method

作者简介：于福江（1989—），男，黑龙江哈尔滨人，硕士研究生，核科学与工程专业＊通信作者：孙喜明，E－mail：xmsun＠tsinghua．edu．cn

基金项目：国家科技重大专项资助项目（ZX06901）

收稿日期：2015－03－09；修回日期：2015－04－08

doi：10．7538／yzk．2015．49．08．1452

文章编号：1000－6931（2015）08－1452－08

文献标志码：A

中图分类号：TG172