基于Riccati方程和不等式方法的H∞控制
2015-03-01谷晓沛李树多
谷晓沛,李树多
(鞍山师范学院 教育科学与技术学院,辽宁 鞍山 114007)
基于Riccati方程和不等式方法的H∞控制
谷晓沛,李树多
(鞍山师范学院 教育科学与技术学院,辽宁 鞍山 114007)
研究了基于Riccati方程和Riccati不等式方法的H∞次优控制,比较了两种方法得到的次优值大小关系,得出一些相关的结论.
H∞控制;Riccati方程;Riccati不等式
代数Riccati方程(简写ARE)在控制系统综合方面起着重要作用,在H2和H∞最优控制理论中扮演着中心角色,下面介绍ARE的有关内容.
设A、Q和R为n×n矩阵且Q和R为对称阵,则称矩阵方程
ATX+XA+XRX+Q=0
(1)
为一个代数Riccati方程.与Riccati方程相关联的一个2n×2n矩阵
(2)
称为Hamilton矩阵.
用dom(Ric)表示Riccati方程的定义域,X=Ric(H)表示X是与H相关的Riccati方程的解.
引理1[1]设H∈dom(Ric)及X=Ric(H),则
(i)X是实对称的;
(ii)X满足Riccati方程ATX+XA+XRX+Q=0;
(iii)A+RX是稳定的.
引理2[1]设H在虚轴上无特征值,R或是半正定的,或是半负定的,则H∈dom(Ric)当且仅当(A,R)是可镇定的.
引理3[1]设H具有形式
则H∈dom(Ric),当且仅当(A,B)是可镇定的以及在虚轴上无不可观的模态.
给定一个Riccati方程,存在许多可能的解,所有解中我们感兴趣的是那些实的、对称的并且是镇定的解,同时也对另外一族解感兴趣,称为极值(最大或最小)解.本节讨论极值解与镇定解之间的关系.
若考虑Riccati方程(1),若X+≥X对方程(1)的所有Hermit解X成立,则X+称为(1)的一个最大解;若X-≤X对方程(1)的所有Hermit解X成立,则X-称为(1)的一个最小解.显然,最大和最小解若存在则必是唯一的.
式(1)的左侧是一个二次型矩阵,定义它为Q(X),则
Q(X)=ATX+XA+XRX+Q.
引理4[1]设R≥0并设存在一个Hermit阵X=XT,使得Q(x)≤0.
(i) 若(A,R)是可镇定的,则Riccati方程(1)存在唯一的最小解X-,进而,对所有使得Q(x)≤0的X,有X-≤X及σ(A+RX-)⊂C-.
(ii) 若(-A,R)是可镇定的,则Riccati方程(1)存在唯一的最大解X+,进而,对所有使得Q(x)≤0的X,有X+≥X及σ(A+RX+)⊂C+.
1 H∞反馈控制
给定线性时不变(LTI)系统状态方程
(3)
其中,x∈Rnp是系统状态变量,u∈Rnu是控制输入,ω∈Rnω是外部输入,y∈Rny是测量输出,z∈Rnz是固定输出.
考虑输出反馈控制器
(4)
其中,ζ∈Rnk是控制变量,闭环系统可描述为:
(5)
状态变量xcl=(xT,ζT)T,传递函数矩阵为
Ccl=(Cz+DzDkCDzCk),Dcl=Dzω+DzDkDω.
1.1 状态反馈
(6)

和
Ps=Ric(H∞)≥0.
进一步,如果这些条件满足,那么u=Fx是一个次优控制器,其中,F=-BTPs.
1.2 输出反馈
(7)
引理6 给定常数γ>0,假设
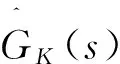

ρ(PsSs)<γ2.
而且,当这些条件成立时,设计控制器
其中,
从引理6可以看出,在H∞次优控制中,控制器的设计依赖于两个Riccati方程的解.下面来研究方程的可解性问题.这里以状态反馈为例.
1.3 方程
考虑方程
(8)
注意到与方程(8)相关的Hamilton矩阵是
(9)

本节重点在基于Riccati方程和Riccati不等式方法的H∞次优控制值比较,因此不妨设X∞=Ric(H∞),则X∞满足Riccati方程
(10)
方程(10)左乘-X∞-1,右乘X∞-1,得到
(11)
P1=Ric(H∞(γ1))≥0,P2=Ric(H∞(γ2))≥0,P1>P2,
那么
γopt<γ1(P1)<γ2(P2),
其中,γ1(P1),γ2(P2)是指由P1,P2设计控制器得到闭环系统的传递函数范数的次优值.
证明 因为P1=Ric(H∞(γ1))≥0,P2=Ric(H∞(γ2))≥0,P1>P2,
(12)
(13)
式(12)减去式(13),得
若当
由此可见,P是关于γ的减函数,因此γ(P+)是所有可能解设计控制器得到闭环系统函数传递函数范数的最小值.
1.4 不等式
考虑系统(6),状态反馈H∞次优控制特征.
引理7[2]γ是次优值的充要条件是存在P>0,使得
(14)
如果P>0满足(14),那么F=-BTP使得γ(F)<γ.
定理2 系统(-ATC)T是可镇定的,那么下列3个陈述等价:
(15)
定理2的证明与定理1的证明过程类似,此处略.
定理3 假设定理2条件成立,那么式(15)的解唯一,最大镇定解P+>0具有性质
定理3的证明与定理1的证明过程相似,此处证明略.
进一步,存在序列Pj∈Sn使得
收敛到P+(j→+∞)并且γ(Pj)→γ(P+).
对于
具有类似的结果,得到关于输出反馈H∞控制结果,这里不再具体陈述.
[1] 周克敏.鲁棒与最优控制[M].北京:国防工业出版社,2006.
[2]CScher.ThesolutionsetofthealgebraicRiccatiequationandthealgebraicRiccatiInequality[J].LinearAlgebra,1991,53:99-122.
[3]GZames.Feedbackandoptimalsensitivity:Modelreferencetransformations,multiplicativeseminormsandapproximateinverses[J].IEEETransactiononAutomaticControl,1981,26:301-320.
GU Xiaopei,LI Shuduo
(SchoolofEducationalScienceandTechnology,AnshanNormalUniversity,AnshanLiaoning114007,China)
(责任编辑:张冬冬)
Based on Riccati equation and inequality methodH∞control
In this paper,we give suboptimal control method based on Riccati equation and Riccati inequality,and compare the relationship between the two methods to get the suboptimal value,and some related conclusions are obtained. Key wordsH∞control;Riccatiequation;Riccatiinequality
2015-08-13
谷晓沛(1974-),女,辽宁鞍山人,鞍山师范学院教育科学与技术学院教师,博士生.
O231.1
A
1008-2441(2015)06-0007-05
