双稳态施密特触发电路在OU噪声驱动下的逻辑随机共振

平明珠,曾宪庭,张 雷

(中国计量学院 信息工程学院,浙江 杭州 310018)

双稳态施密特触发电路在OU噪声驱动下的逻辑随机共振

平明珠,曾宪庭,张 雷

(中国计量学院 信息工程学院,浙江 杭州 310018)

噪声能够帮助非线性系统产生反常的有序行为的现象吸引了人们的广泛关注.我们以一个双稳态的施密特触发电路作为模型系统,用OU(Ornstein-Uhlenbeck)噪声驱动,利用噪声进行逻辑计算,实现了逻辑门的模拟运算.同时研究了噪声强度、噪声相关时间下的逻辑随机共振,并且探讨了系统的弛豫性质对逻辑随机共振的影响.结果表明,色噪声驱动下的双稳态系统中的逻辑随机共振现象同样存在.

OU噪声;逻辑随机共振;非线性系统;双稳态

噪声对非线性系统的影响中,最重要的是随机共振.即,适量的噪声能够有效地增强非线性系统的输出响应.受到随机共振能够使得非线性系统的输出响应增强的启发,研究者将随机共振理论用于逻辑计算.随着芯片制造技术纳米尺度化的趋势,无处不在的噪声对计算设备性能的影响会变得越来越严重,譬如精度、速度和能耗方面的影响[1-2].最近Murali等人[3]通过调节双稳态系统的阈值改变其势阱的对称性,发现了设备噪声和非线性系统之间的相互作用,即逻辑随机共振现象[4].逻辑随机共振的实验模型是由线性电阻、线性电容和COMS元件组成的非线性电子电路[5].Guerra等人[6]指出,逻辑随机共振也可以在一些纳米级的系统中存在,纳米逻辑门的设计具有极大的潜力.Zamora-Munt[7]等人将随机共振逻辑门应用在垂直腔面发射激光器(VCSEL)上.Fierens[8]等人提出了一个环形的施密特触发器,实现了一个噪声支持的异步存储设备.

在以往的研究中,通常假定噪声的相关时间远远小于系统的内在时间尺度,因此噪声被认为是与强度相关的高斯白噪声[9],这是一种近似理想的模型.实际上,尽管大量的色噪声广泛地存在于现实场景中,然而,色噪声的相关时间和系统的弛豫性质对于在电子计算设备性能上的影响从未被探讨过,专注于色噪声的逻辑随机共振的问题是非常重要的[10].基于此,研究双稳态施密特触发电路在OU(Ornseein-Uhlenbeck)噪声驱动下的逻辑随机共振现象,通过改变噪声强度和相关时间来探讨逻辑随机共振现象,以及电子弛豫性质对逻辑随机共振的影响十分有必要.本文以逻辑输出的成功率作为逻辑随机共振的测度,着重研究了色噪声的逻辑随机共振问题,验证了在双稳态系统中色噪声驱动的逻辑随机共振也存在.

1 双稳态施密特触发电路模型

施密特触发器存在正向阈值电压与负向阈值电压,有两个稳定状态,属于典型的双稳态系统.基于此,我们利用施密特触发器设计了随机共振的逻辑计算实验平台.图1表示的是基于施密特触发器的逻辑门设计原理图.

图1 由输入信号和噪声驱动的施密特触发器示意图Figure 1 Schematic diagram of the Schmitt trigger driven by input signal and noise

简单的施密特触发器可以由一个运算放大器和一对精选的电阻组成.电路中的运算放大器作为一个比较器.

(1)

如果V+-V->0,输出Vout为正,反之为负.在该电路中,当阈值电压V+-V-=0时,即理想状态下,施密特触发器两个状态之间的切换时间为0,可以表示为

(2)

其中，y=Vou/Vmt,z=(V+-V-)/Vm.不失一般性,忽略系统的滞后性质,逻辑输入和噪声驱动的理想化施密特触发电路的模型为:

y=sign(γy-I(t)-x);
x=σ′ξ(t).

(3)

其中:σ′=Vn/Vm,是规格化的噪声强度;ξ(t)是均值为0方差为1的高斯白噪声;定义I(t)=I1(t)+I2(t)+ε,I1(t)和I2(t)是两个随机切换的方波;ε是添加的偏置信号,改变双稳态系统的对称性,从而实现了逻辑随机共振现象;噪声x(t)是噪声强度为σ′的高斯白噪声ξ(t)的统一表示.由于正向反馈电压的一部γ=R1/(R1+R2)会加入回路,因此施密特触发器的输出通常带有一定的滞后性.理想的施密特触发器两稳态切换时间为0,这需要无穷大的能量来实现,在现实的场景中不存在.鉴于这个原因,x(t)将被建模为一个具有有限相关时间τc的色噪声,如果系统的切换时间比τc大,那么就舍弃原双稳态模型,使用二维连续函数代替.为了避免白噪声的能量无限大,同时让噪声强度更加接近真实,施密特触发电路的动态方程可以表示为一个如下的二维系统:

(4)

2 基于施密特触发电路的逻辑随机共振实验

McNamara等人已用上述方程探讨过双稳态系统中的经典随机共振[4].本文也将用这个模型来研究逻辑随机共振.不失一般性,当二次方波I1(t)和I2(t)的电平值为0.2时,逻辑输入为1,当电平值为-0.2时,逻辑输入为0.I1(t)和I2(t)只有4种不同的输入组合,即(I1,I2)∶(0,0),(0,1),(1,0)和(1,1).鉴于(0,1)和(1,0),I1(t)与I2(t)的和有相同的值,所以4个逻辑输入组合可以简化成3个.输入I(t)=I1(t)+I2(t)编码为三方波,值-0.4相当于输入设置为(0,0),值0相当于输入设置为(0,1)/(1,0),值0.4相当于输入设置为(1,1)[3,7].系统的逻辑输出由系统的输入状态决定,当双稳态系统处于其中一个势阱(x+)时,系统的逻辑输出可以被认为是0,位于另一个势阱时(x-),系统的逻辑输出被认为是1;反之亦可.观察发现,逻辑输出总保持三个逻辑0和一个逻辑1,或者三个逻辑1和一个逻辑0.根据亚阈值随机共振,在噪声的帮助下,总能通过调节双稳态系统的势阱深度,改变系统的对称性.在3级非周期信号的驱动下,使逻辑输入集中的3个逻辑输入集合偏向一个势阱,另一个逻辑输入集偏向另一个势阱.根据这种方式,可以模拟出任意的逻辑门.如基本的逻辑关系真值表1和图2.

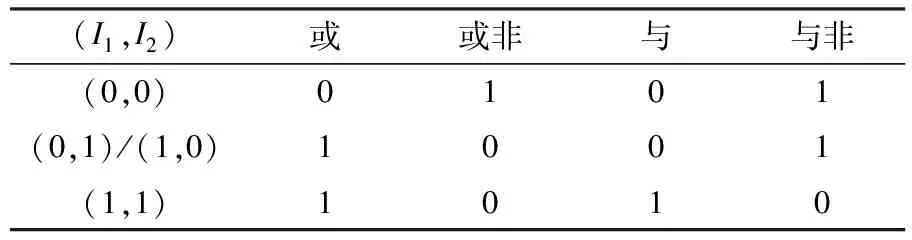
表1 基本逻辑关系真值表

图2 不同噪声强度D的系统输出响应Figure 2 Response of the system of different noise intensity of D

而逻辑系统的可靠性可以按如下方式获得:通过计算机产生模拟值,每次输入不同的(I1,I2)逻辑组合来驱动系统,它的输出流通过基本逻辑关系真值表来检验,当且仅当输出的正确率高于一定的比例时,此次逻辑输出视为正确,否则视为失败[8].成功概率P=正确的运行次数/总的运行次数,需要通过超过100 000次以上的数值模拟得到.

3 色噪声的噪声强度对逻辑随机共振的影响

实验以NAND逻辑关系为例,实现双稳态系统的逻辑输出流.输入信号(0,0),(0,1)/(1,0)时的系统逻辑输出状态(x-),结果取逻辑1;输入信号(1,1)时的系统逻辑输出状态(x+),结果取逻辑0.当噪声强度较低时,驱动信号电平较低,难以越过系统阈值,系统并未在两稳态间切换,双稳态系统未能进行任何有效的逻辑计算,如图3.逐步增加噪声,双稳态系统的输出响应才逐步地显现出来.逻辑组合信号能够越过系统阈值进行状态切换,双稳态系统最终能够成功模拟出逻辑门.

图3 逻辑输出成功率与噪声强度D(X轴,单位V)和偏置系数ε的关系图Figure 3 Density map of P(logic) as a function noise intensity D and input bias ε

可以通过调节非线性系统的偏差参数来获得不同的逻辑门.图4显示出系统的逻辑输出成功输出率对于噪声强度D和系统偏置系数ε的函数关系谱.其中,x轴表示噪声强度(单位V),y轴表示偏差参数.给定的噪声相关时间τc=5,A=10 000,β=100,N=320 000和γ=0.4.从函数关系谱中,可知当D不在最佳值时可以通过调节偏置系数ε来使得系统获得最佳逻辑输出性能.

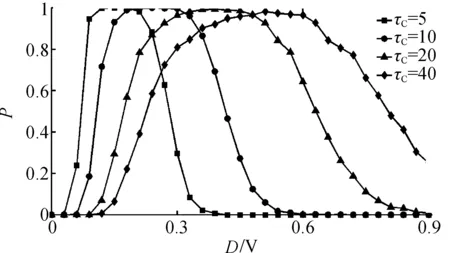
图4 不同的噪声相关时间下成功率P对于噪声强度D的曲线Figure 4 Success probability P(logic) versus noise intensity D at different correlation time τc

4 色噪声的相关时间对逻辑随机共振的影响

各类色噪声广泛地存在于电路或纳米器件中.色噪声不可避免地对逻辑门器件产生影响.所以研究色噪声驱动的逻辑随机共振现象是本文的一个重点,着重对指数相关的Ornstein-Uhlenbeck(OU)噪声驱动的非线性系统的逻辑计算性能进行了分析.

在OU噪声的驱动下,我们首先研究了噪声强度D对逻辑随机共振的影响.图5描绘了噪声强度为D,不同相关时间τc时成功率P的曲线.从该曲线我们可以看到,曲线成反向U型,P随着噪声强度的增加先上升,后下降.给定τc=5和τc=10,在一定范围强度的色噪声的驱动下,系统的逻辑输出表现出噪声平台效应,即在适当的噪声强度范围下,成功率P保持在近似为1的水平.说明系统的逻辑输出在合理的扩大噪声强度范围内可以精确获得.当τc增加时,峰值会降低,最佳噪声范围后移,反向U型曲线变得更宽,在强噪声的驱动下,使τc=20和τc=40时,我们发现峰值性能衰减到100%以下.事实上,仍然存在一个峰值,但是下降了一些,并且不完全平,在适当相关时间的色噪声下仍然可以获得准确的逻辑输出.结合基本逻辑随机共振原理,从以上的实验结果可以证明OU噪声驱动的施密特触发电路可以诱导逻辑随机共振现象.

图5 不同的噪声强度下成功率P对于噪声相关时间的曲线Figure 5 Success probability P(logic) versus correlation time τc at different noise intensity D

此外,我们还研究了噪声的相关时间τc对逻辑随机共振的影响.图6描绘了4种不同的噪声强度下,噪声相关时间对于P影响.可以看出,给定噪声强度,P对于相关时间τc是不单调的函数,这是一个显著的随机共振现象.当噪声强度增加时,反向U型曲线变得更宽,相关时间的最佳范围变宽,峰值性能降低.结果显示,想获得所需逻辑计算成功率有时可以通过调节相关时间来改善,而不仅仅是调节噪声强度D.在设计方面,低的相关时间往往效果更好.图7是通过数值模拟计算出的成功率对于噪声强度D和噪声相关时间τc的面积图.该图显示,对逻辑随机共振的效果影响可以通过两种方式:一是改变噪声强度D;二是改变噪声相关时间τc.

图6 逻辑输出成功率P对噪声强度D(x轴)和相关时间τc(y轴)的函数关系谱图Figure 6 Density map of P(logic) as a function noise intensity D and correlation time τc

5 系统的弛豫性质对逻辑随机共振的影响

通常情况下,当输入进行切换时,系统需要一个时间从原稳定输出状态切换到新稳定输出状态,我们称这个时间段为系统弛豫时间.在这个弛豫时间段内,所采样的逻辑输出通常是不稳定的.在弛豫时间段之后,系统才达到新的稳定状态,才能进行有效的采样.

在实际的施密特触发电路中,系统从一个状态到另一个状态,系统的弛豫率为一个恒定的时间指数1/β[8].我们在施密特触发电路的模型上研究了系统的弛豫率对逻辑随机共振的影响,如图7.可以看出,在给定噪声相关时间τc=50,不同系统弛豫率的情况下描绘了成功率P对于噪声强度D的函数,P先增加,然后当噪声强度达到某一值时,P下降.结果表明,在不同的弛豫率下,逻辑随机共振现象仍然存在.当β上升时,反向U型曲线变得清晰,最佳性能上升,曲线的最佳平稳状态明显增强.事实上,由于弛豫率的存在,系统对新的输入作出响应通常需要时间,过了一个反应时间,逻辑输出采样才是正确的.因此当β增加时,逻辑随机共振的性能增加.

图7 五种不同的弛豫率β下P对于噪声强度D的曲线Figure 7 Success probability P(logic) versus noise intensity D at different relaxation rate β

6 结 语

本文用双稳态施密特触发电路建模二维连续系统,研究了色噪声的逻辑随机共振问题.实验结果显示噪声强度与噪声的相关时间都是诱导逻辑随机共振的重要因素.逻辑随机共振成功率随着噪声强度改变而改变,过大或者过小都会导致共振效果不佳.同样,逻辑随机共振成功率与噪声相关时间函数曲线成反向U型,并且存在峰值平台效应.另外也探讨了电子弛豫性质对逻辑随机共振的影响,结果显示逻辑随机共振的性能在弛豫率β增强时能有效地增强.

[1] XU Yong, JIN Xiaoqin, ZHANG Huiqing. The availability of logical operation induced by dic-hotomousnoise for a nonlinear bistable system[J].Journal of Statistical Physics,2013,152(4):753-768.[2] WANG Nan, SONG Aiguo. Logical stochastic resonance in bistable system under alphast ablenoise[J].European Physical Journal B,2014,87(5):117-118.

[3] MURALI K, KAHAR V, SINHA S. Enhanced logical stochastic resonance under periodic forcing[J].Communications in Nonlinear Science and Numerical Simulation,2014,19(8):2866-2873.

[4] MCNAMARA B, WIESENFELD K. Theory of stochastic resonance[J].Physical Review A,1989,39(9):4854-4860.

[5] WANG Nan, SONG Aiguo. Set-Reset latch logical operation induced by colored noise[J].Physics Letters A,2014,378(22):1588-1592.

[6] GUERRA D N, BULSARA A R, DITTO W L, et al. A noise-assisted reprogrammable nanomechanical logic gate[J].Nano Letters,2010,10(4):1168-1171.

[7] ZAMORA-MUNT J, MASOLLER C. Generation of optical pulse in VCSELs below the static threshould using asymmetric current modulation[J].Optlcs Express,2008,16(22):17848.

[8] RAMON J, CROONENBORGHS T, GENERALIZED D. Ordering-search for learning directed probabilistic logical models[J].Machine Learing,2008,70(2):169-188.

[9] SHARMA A, KOHAR V, SHRIMACI M D. Realizing logic gates with time-delayed synthetic genetic networks[J].Noninear Dynamics,2014,76(1):431-439.

[10] 张雷,宋爱国.基于随机共振的逻辑计算理论回顾与展望[J].仪器仪表学报,2011,32(10):10-15. ZHANG Lei, SONG Aiguo. Review and prospect of logic computation basic on stochastic resonance[J].China Journal of Scientific Instrument,2011,32(10):10-15.

Logical stochastic resonance in quasi-static Schmitt trigger circuits driven by the Ornstein-Uhlenbeck process

PING Mingzhu, ZENG Xianting, ZHANG Lei

(College of Information Engineering,China Jiliang University,Hangzhou 310018, China)

It has become increasingly clear that noise can play a constructive role in helping nonlinear dynamical systems to produce counterintuitive ordered behavior. We used the noise to drive computing, in which the realization of the logic gate was demonstrated in a quasi-static Schmitt trigger circuit by cycling various combinations of two logic inputs driven by Ornstein-Uhlenbeck noise. Two major kinds of logical stochastic resonance effects were presented by changing the noise intensity, as well as by changing the correlation time respectively, and the effect of the electronics relaxation rate on the LSR was also discussed. The study provides an example that LER can exist robustly in the quasi-static system in the presence of colored noise.

Ornstein-Uhlenbeck noise; logic stochastic resonance; nonlinear dynamical systems; quasi-static system

1004-1540(2015)03-0295-05

10.3969/j.issn.1004-1540.2015.03.009

2015-04-14 《中国计量学院学报》网址：zgjl.cbpt.cnki.net

国家自然科学基金资助项目(No.61203237),中国博士后科学基金资助项目(No.2011M500836),浙江省自然科学基金资助项目(No.LQ12F03016).

平明珠(1991- )，女，安徽省滁州人，硕士研究生，主要研究方向为随机共振.E-mail：2940716696@qq.com 通讯联系人：张 雷，男，副教授．E-mail：810992774@qq.com

TP391

A