EMD与JADE相结合的算法及验证

2015-02-27郭天太吕晨焕

中国计量大学学报 2015年3期

关键词：断齿变速器分量

吴超,赵军,郭天太,吕晨焕

(中国计量学院计量测试工程学院,浙江杭州 310018)

EMD与JADE相结合的算法及验证

吴超,赵军,郭天太,吕晨焕

(中国计量学院计量测试工程学院,浙江杭州 310018)

针对汽车变速器齿轮在长时间高强度工作状态下易产生故障的问题,提出了一种基于经验模式分解(EMD)和盲源分离算法中的特征矩阵联合近似对角化法(JADE)相结合的汽车变速器齿轮故障诊断算法.首先,将振动信号进行EMD分解,再根据互相关准则对分解后的本征模分量进行重构,构造虚拟噪声信号,并以此作为JADE的输入矩阵;然后,采用JADE算法分离得到能清晰反映齿轮状态的特征信号.最后将该方法应用于汽车变速器齿轮故障诊断中,仿真和实测分析结果均表明该方法有效可行.

经验模式分解;互相关准则;特征矩阵联合近似对角化法;齿轮故障诊断

齿轮对于旋转机械设备来说是必不可少的,它能够起到部件与部件之间的连接作用并且能够传递机械动力.其工作状况健康与否关系着整个机器的运转质量,但由于齿轮长期处在恶劣的工作环境中,在大量背景噪声下故障信号表现微弱.所以,怎样从强噪声信号中分离出其有效特征信号,是判断齿轮健康与否的关键.

近年来,在微弱信号提取的研究上,唐贵基等利用谐波小波在频域连续分布且具有严格的盒形谱特性,实现了对微弱信号的频域提取[1];陈彦龙等在阈值处理基础上,结合离散余弦变换重构信号,提取出了微弱故障信息[2];朱世欣等提出了一种基于奇异值分解和经验模态分解的微弱信号提取方法[3];针对特征信号难以提取问题,周昊等提出了一种基于粒子群优化的盲源分离算法[4].

盲源分离算法最早是由法国学者Jutten和Herault提出的[5].当时还不能实现两个以上的混叠源信号分离,在非线性函数的选取上也比较随意,缺乏理论依据.在此基础上,Comon全面分析了关于瞬时混叠信号的盲源分离问题,明确了独立分量分析的概念,得到一类基于特征分解的独立分量分析方法[6].如今,有许多行之有效的盲源分离算法,如JADE、Infomax(一个基于最大信息判据的盲源分离算法程序)、快速ICA算法等.其中,JADE算法鲁棒性好,且通常可获得较稳定的源估计结果[7-9].但JADE算法同其他盲源分离算法一样,为达到分离出真实噪声信号的目的,一般需要构造虚拟噪声.然而,JADE算法只能消除原始信号中与虚拟噪声相匹配的真实噪声成分,由于真实噪声信号是未知的,构造与其相匹配的虚拟噪声很难,如果构造的虚拟噪声与真实噪声匹配度不高,消噪效果就会不理想.目前,只能用试配方法来构造虚拟噪声.而EMD能够将原始信号分解成多个本征模分量,每个本征模分量与原始信号的相关性各不相同,与原始信号相关性小的本征模分量与真实噪声信号的相关性可能就大,所以想到可以用与原始信号相关性小的本征模分量的和来构造JADE算法所需的虚拟噪声.基于上述思想,我们提出了一种基于经验模式分解(EMD)和特征矩阵联合近似对角化法(JADE)的汽车变速器齿轮故障诊断算法，并且通过仿真及实测信号分析,证明了其有效性.

1 基于EMD-JADE理论模型的建立

1.1 EMD的基本原理

EMD的主要思想是把一个时间序列的信号分解为不同尺度的本征模分量(intrinsic mode function,IMF),它最早由美国学者Huang于1998年提出[10].任何一个IMF都要满足下面两个条件:

1)时域图上,极值点与过零点个数之差的绝对值不大于1.

2)局部极大值点和局部极小值点分别形成的包络线的均值为0.

EMD分解的具体步骤如下:

1)把信号记为x(t),让其上包络线及下包络线的局部均值组成序列m(t).

2)令h1(t)=x(t)-m(t),若h1(t)满足IMF条件,则其为第一个IMF分量;反之将h1(t)作为原始数据重复步骤(a)和(b)k次,h1k(t)=h1(k-1)(t)-m1k(t),使h1k(t)满足IMF条件获得第一个IMF,记作c1(t)=h1k(t).

3)从x(t)中减去c1(t),得到残差

r1(t)=x(t)-c1(t).

(1)

将r1(t)作为原始数据重复上面步骤,提取x(t)的下一个分量c2(t).剩下的分量可以用相同的步骤提取,直到rn(t)变成单调函数,循环结束,提取到n个IMF分量.最终信号x(t)可以表示为

(2)

EMD分解的主要缺点在于存在模态混叠现象,当出现模态混叠时,不同的物理过程会表现在同一个IMF分量上,以致严重影响EMD的分解效果[11].

1.2 JADE的基本原理

JADE算法是由法国人Cardoso提出的一种建立在“四阶累积量矩阵对角化”概念基础上的独立分解改进算法.JADE算法的具体步骤如下.

步骤1:对观测信号进行球化处理.

对于N个不同的源信号经过一个未知满秩的M×N的混合矩阵A,得到M个观测信号,如下式:

x(t)=[x1(t),x2(t),…,xM(t)]T.

(3)

式(4)为矩阵转化等式

z(t)=Wx(t)=WAs(t)=Us(t).

(4)

式(4)中:W—球化矩阵,其估计值可通过观测信号的自相关矩阵的特征值分解得到[12];U—一酉矩阵.从而,一个M×N混合矩阵A的确定问题转变为一个N×N酉矩阵U的确定问题.

步骤2:计算式(4)中Z的四阶累积量.

对于任意N×N矩阵M,其四阶累积量矩阵V定义为

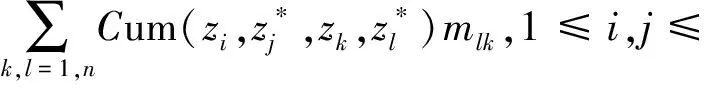
(5)

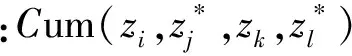
步骤3:优化步骤,联合对角化Z的四阶累积量,得到酉矩阵U.

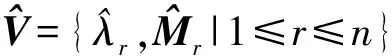
(6)

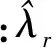
(7)

1.3 EMD-JADE理论模型

为得到能够清晰反映有效特征的信号,在EMD、JADE基本原理的研究基础上,通过互相关准则[13]筛选IMF分量构造虚拟噪声作为JADE的输入矩阵,建立EMD-JADE理论模型.具体步骤如图1.

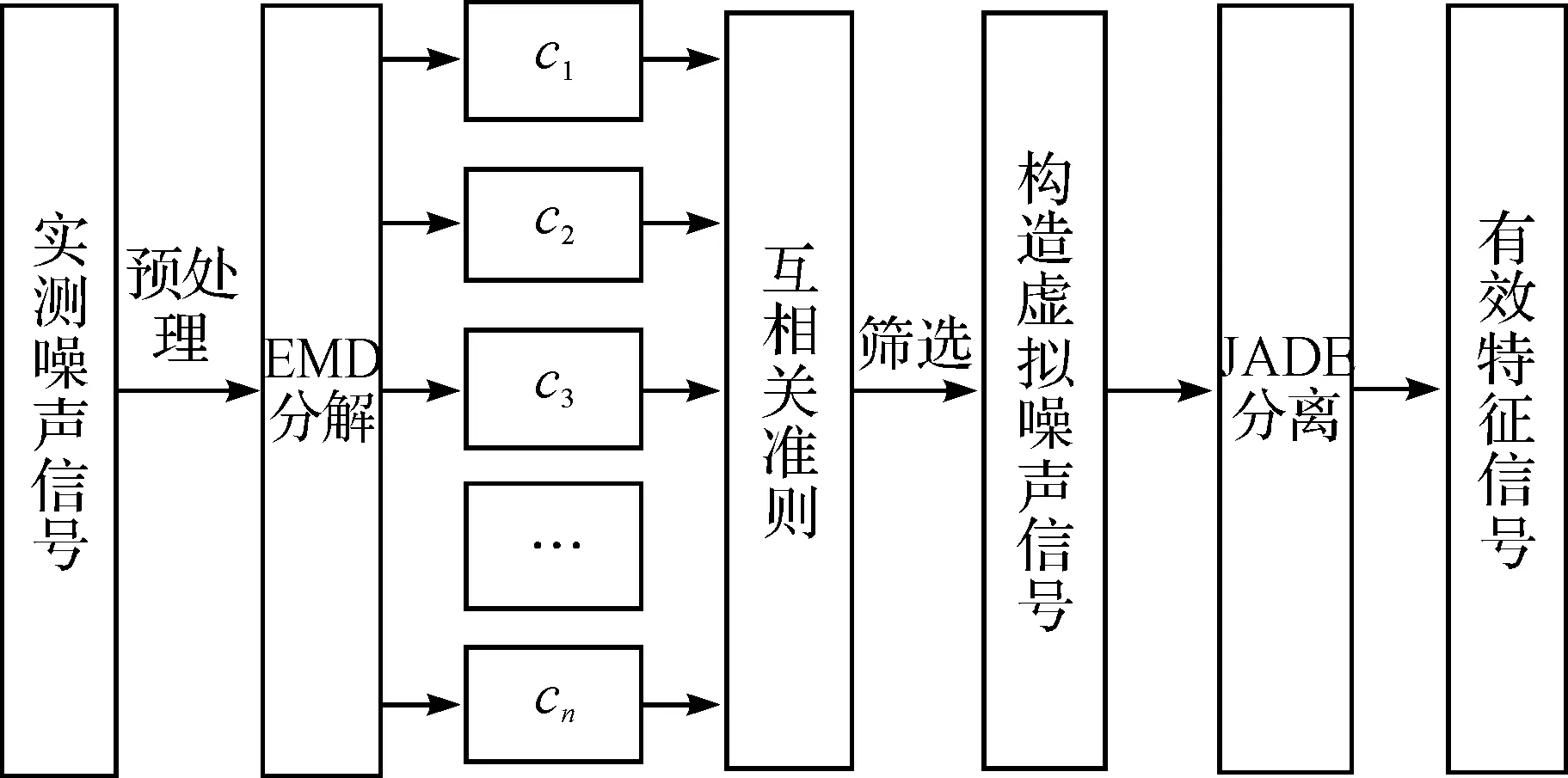
图1 EMD-JADE算法Figure 1 Algorithm of EMD-JADE

2 算法典型信号仿真应用

用仿真实验验证EMD-JADE算法的降噪效果,仿真信号表达式如下式:

s(t)=0.3cos(60πt+0.5sin(30πt))+0.2sin(240πt).

(8)

仿真信号的时频图如图2.采样频率fs=3 000 Hz,采集的数据长度为N=1 000.

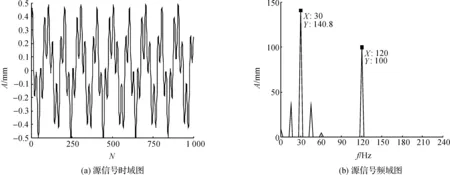
图2 源信号时频图Figure 2 Time-frequency diagram of source signal

让该信号受到一个高斯白噪声N(t)的干扰,记加入噪声后的信号为SN(t),即加噪信号,相应的时频图如图3.由图3可知,不论从时域图还是频域图上已经找不到原来仿真信号的突出特征.

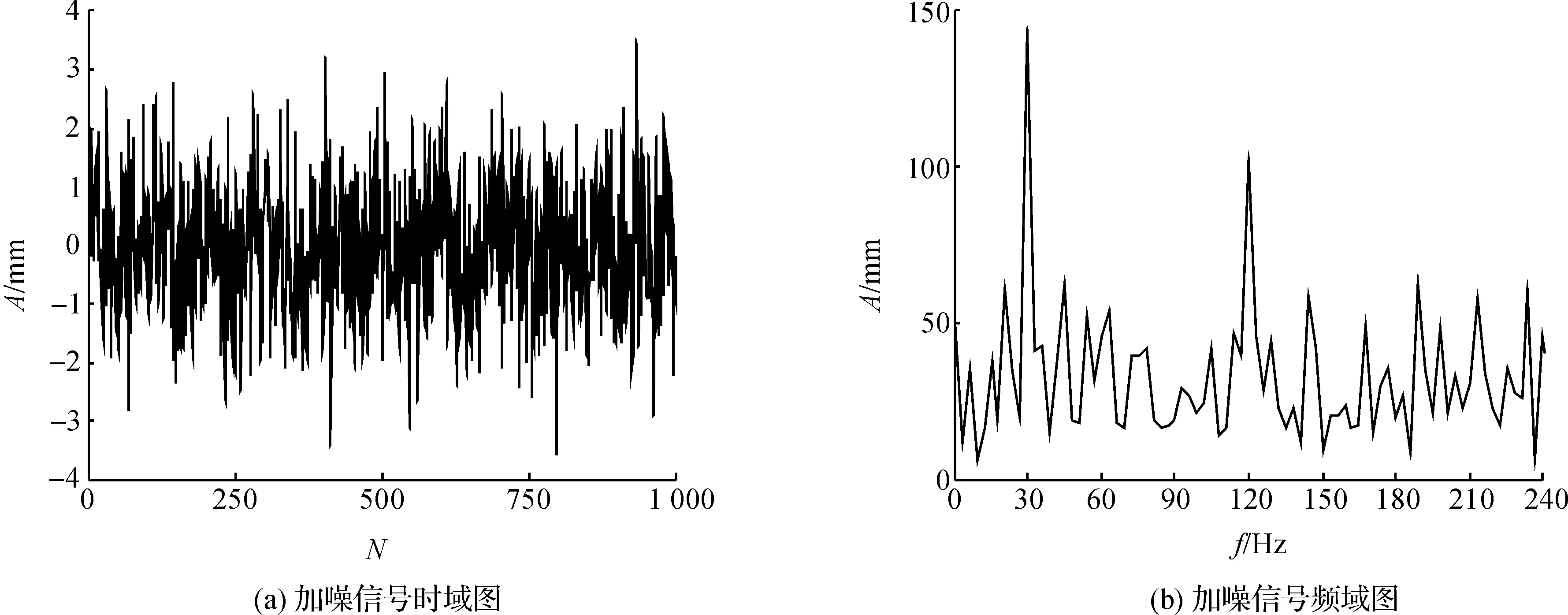
图3 加入噪声后的信号时频图Figure 3 Time-frequency diagram of signal with added noise

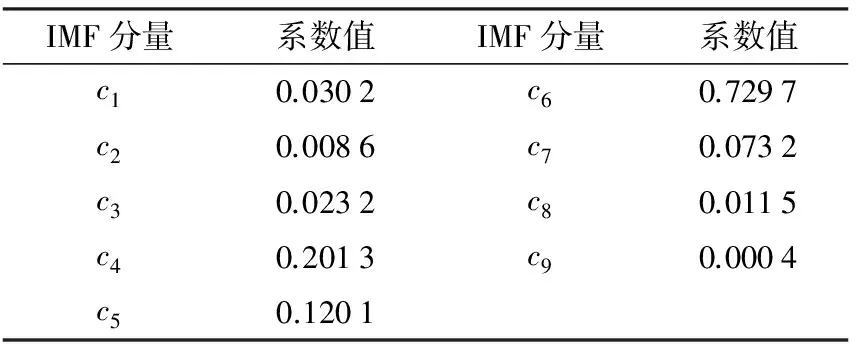
为消除噪声影响,突显源信号,采用EMD-JADE算法,构造合适的虚拟噪声是其关键所在.由于真实噪声信号未知,如果继续采用试配方法来构造虚拟噪声,当构造的虚拟噪声与真实噪声不匹配时,消噪效果不明显.在此,先对加噪信号进行EMD分解,得到相应的IMF分量,然后根据互相关准则计算各IMF分量与源信号的互相关系数,各系数值如表1.

由表1中的互相关系数可以发现c4、c5、c6与源信号的互相关系数较大,最接近真实的仿真信号,剩下的与源信号互相关系数较小的IMF分量就有可能保留了真实噪声成分.JADE消噪能够消除加噪信号中与虚拟噪声信号相匹配的真实噪

表1 IMF分量与源信号的互相关系数

Table 1 Mutual correlation coefficients of IMF components and source signal

IMF分量系数值IMF分量系数值c10．0302c60．7297c20．0086c70．0732c30．0232c80．0115c40．2013c90．0004c50．1201

声成分,所以将除c4、c5、c6外余下的ci叠加,构造虚拟噪声n1(t),得到输入矩阵X=[SN(t);n1(t)],再采用JADE进行消噪,分离信号的时频域图如图4.

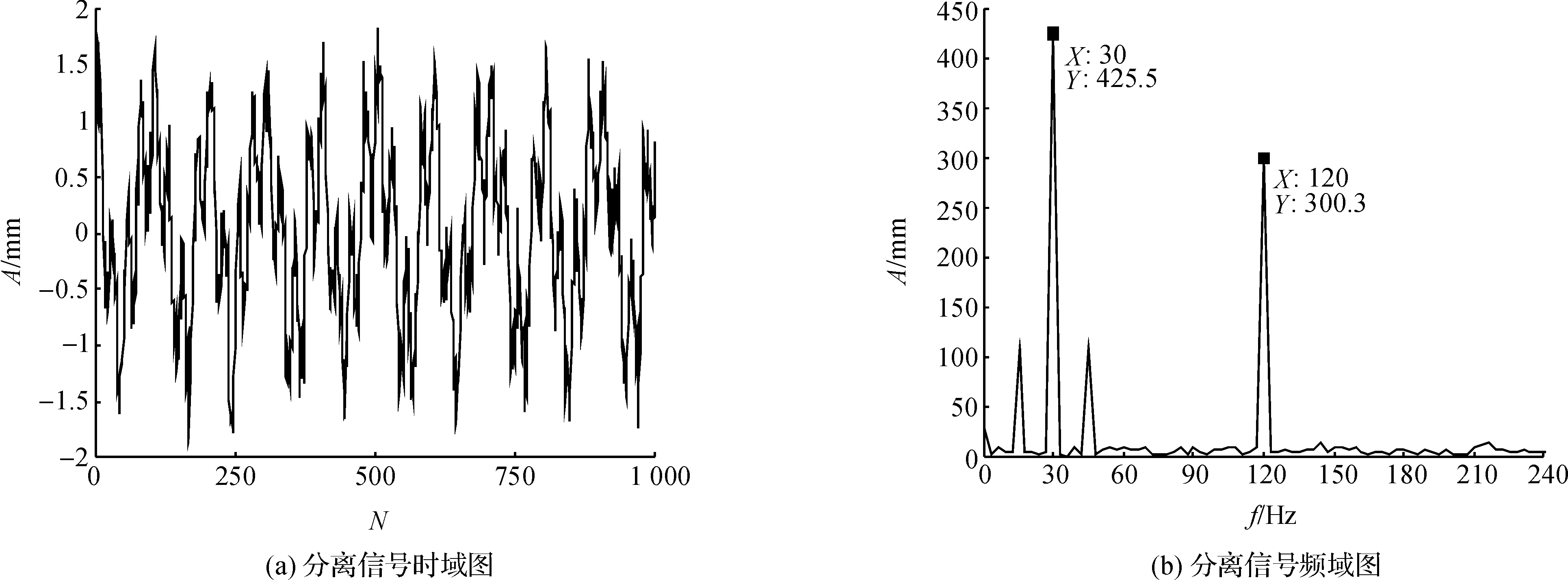
图4 分离信号时频图Figure 4 Time-frequency diagram of separated signal

对比分析图3与图4得出,用上述思想构造虚拟噪声的消噪效果非常好,分离信号能够完全突显出原仿真信号的特征信息.因而,证明了EMD-JADE算法拥有强大的信噪分离能力.

3 算法的实际信号应用

为验证EMD-JADE算法在实测信号分析中的有效性,搭建了齿轮实验平台并采集实际信号进行研究分析.

3.1 齿轮实验平台

实验在如图5的汽车变速器振动分析台架上进行.

图5 变速器振动分析台Figure 5 Vibration analysis platform of transmission

实验用某型汽车变速器为手动全同步换档横置前驱机械式变速器,有5个前进档和1个倒档,Ⅰ轴为主动轴,Ⅱ轴为从动轴,结构简图如图6.实验通过变频电机模拟汽车变速器总成的动力输入,能够在不同条件下进行模拟实验,传感器选用PCB-356A33型压电式三向加速度传感器,数据采集卡为研华PCI-1714UL型,每通道信号初始采样频率为80 kHz.

图6 变速器结构简图Figure 6 Structure diagram of transmission

3.2 实测信号分析

存在断齿故障的变速器产生的振动信号最主要特征是:如果某对齿轮副中某个齿轮存在断齿故障,信号频谱图中会出现以故障齿轮副的啮合频率及其谐波作为载波频率,固定故障齿轮的转轴轴频及其倍频作为调制频率的啮合频率调制,调制边频带形状宽且幅值高.

为模拟断齿这种齿轮常见的失效形式,本实验用电动磨具在变速器Ⅱ轴2档齿轮上仿制了一个断齿故障,2档齿轮为图6中“*”所在位置,断齿故障如图7.利用上述的实验平台,采集电机转速为900 r/min及变速器在2档位置的正常及断齿故障振动加速度信号,开机预热时间为10 min,台架振动通过减振装置保证.变速器Ⅰ、Ⅱ轴2档齿轮齿数分别为Z1=21、Z2=43.在上述转速下,计算得到变速器2档齿轮副理论啮合频率fz=315 Hz,Ⅱ轴理论轴频fr=7.32 Hz.

图7 不同角度断齿故障展示Figure 7 Display of broken teeth fault from different angles

本实验对实际采集的振动信号前131072个数据量进行分析,得到正常振动信号及断齿故障信号的时域图及功率谱如图8.由图8(c)和(d),信号信息杂乱,根本无法判断变速器齿轮的真实状态.接着将图8(c)的采集信号进行EMD分解,得到17个IMF分量.最后,根据互相关准则得到所有IMF与所采集信号的互相关系数,具体系数值见表2.

从表2中的互相关系数值来看,c1～c9保留了原始信号中较多的状态特征,所以,将余下的IMF分量求和,构造虚拟噪声信号n2(t),作为JADE的输入矩阵,经过EMD-JADE降噪后的信号功率谱如图9(a)所示,图9为不同算法的降噪效果对比结果.图9(b)为互相关系数值最大的c4的功率谱,在图中完全看不到有用的故障特

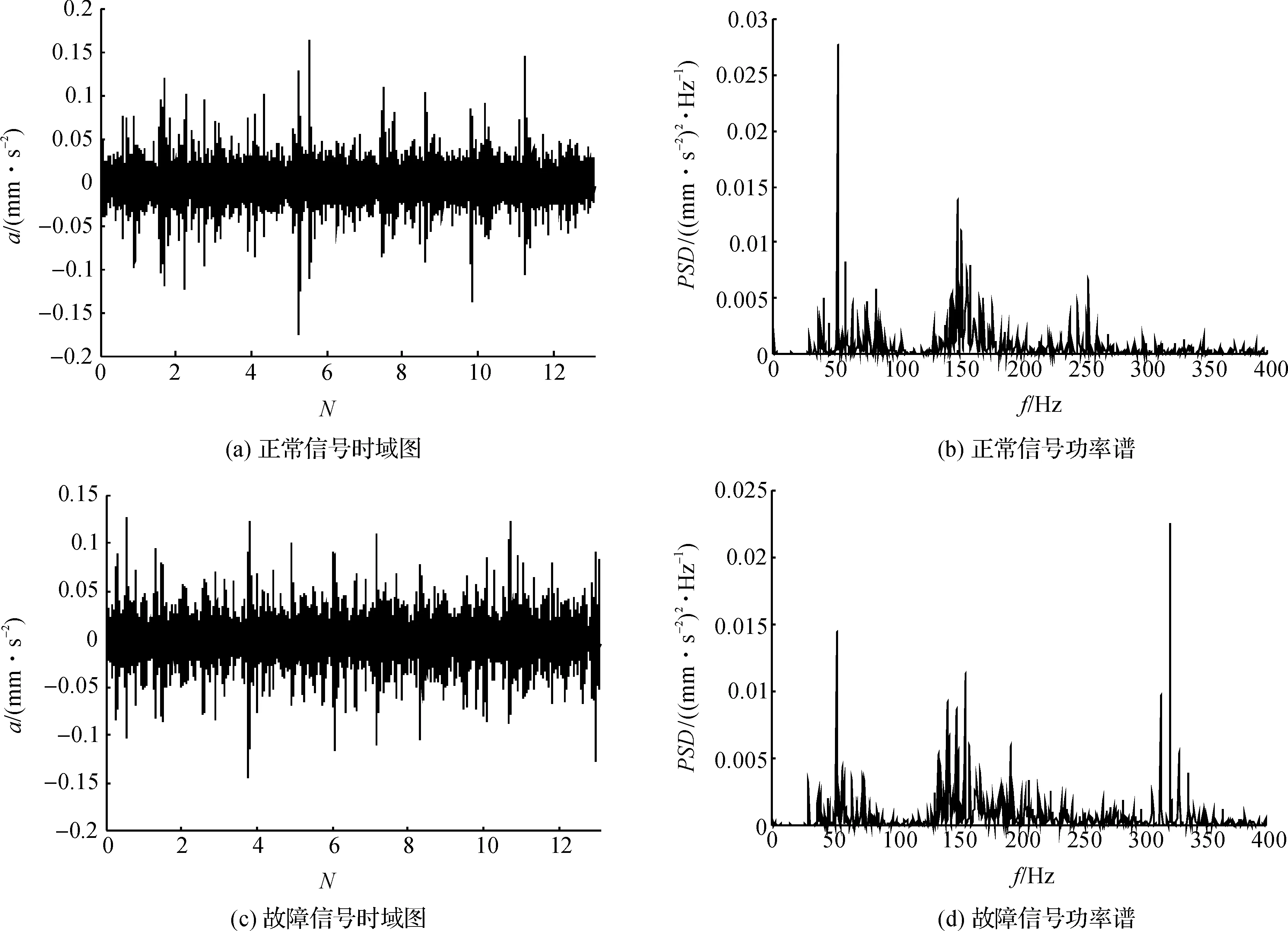
图8 原始信号时域图及功率谱Figure 8 Time-domain plot and power spectrum of original signal

Table 2 Mutual correlation coefficients of IMF components and original signal

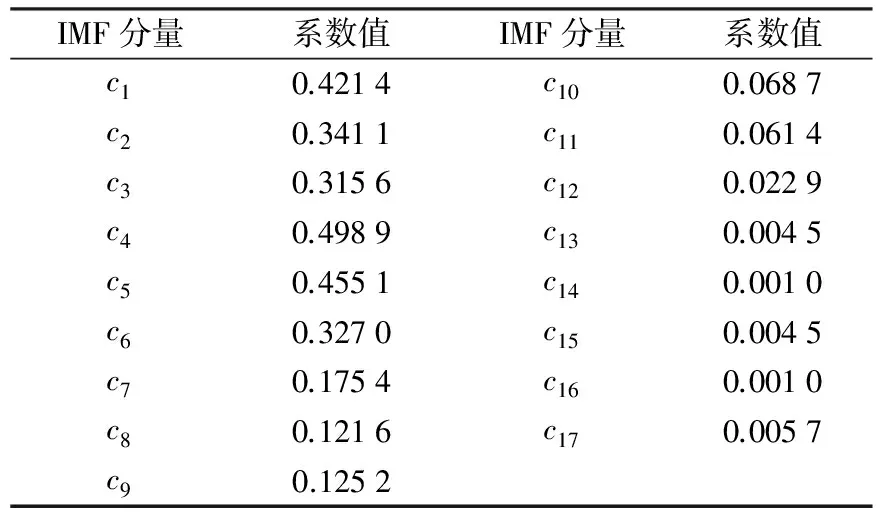
IMF分量系数值IMF分量系数值c10．4214c100．0687c20．3411c110．0614c30．3156c120．0229c40．4989c130．0045c50．4551c140．0010c60．3270c150．0045c70．1754c160．0010c80．1216c170．0057c90．1252

征信息.然后,观察每个IMF分量的功率谱,结果发现只有在c8的功率谱中能够找到接近理论啮合频率fz=315 Hz的特征频率315.9 Hz,但调制边频带不明显,如图9(c).虽然跟图8(b)相比有了一定的消噪效果,但还是不能就此判断齿轮故障的存在.如果在中加入c8,重新构造一个虚拟噪声n3(t)作为JADE输入矩阵,分离后的功率谱如图9(d).对比图9(a)可见,真实噪声成分没有得到很好的消除.

而在图9(a)的功率谱中可以明显看到调制边频带的存在,其中fz=315.2 Hz(理论值315 Hz);fz+fr值为322.6 Hz,得到fr=7.4 Hz(理论值7.32 Hz);从图9(a)中还可以得到fz-fr=308.5 Hz,fz+2fr=329.3 Hz,fz+3fr=337.2 Hz,fz+6fr=358 Hz,fz+7fr=365.3 Hz.从中计算得到的fr值均接近理论值7.32 Hz.

如果变速器存在断齿故障,外界载荷以及转速的变化都会影响调制边频带的分布状况,所以出现边频带的幅值高于啮合频率的幅值现象也正常[14].

至此,根据变速器发生断齿时的振动信号特征结合图9(a)判断,在Ⅰ轴转速为900 r/min时,变速器2档齿轮副存在故障,且故障齿轮所在轴为Ⅱ轴(依据调制频率fr判断).这一结果与本实验模拟的断齿故障位置相符合,从而证明EMD-JADE算法适用于汽车变速器的齿轮故障诊断.并且,通过图9(a)与图9(b)、图9(c)的对比,证明该算法相对于传统的EMD分解有着明显的优势;通过图9(a)与图9(d)的对比,证明了EMD-JADE算法在构造盲源分离算法虚拟噪声时的优势.

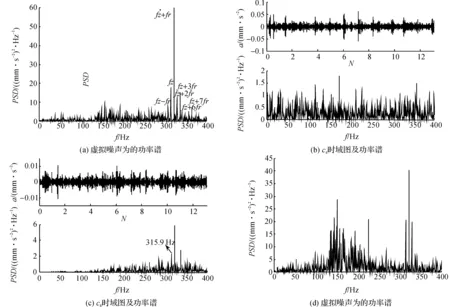
图9 不同算法的对比Figure 9 Comparison of different methods

4 结语

本文在JADE算法的基础上结合EMD分解和互相关准则,得到一种EMD-JADE算法,通过跟EMD降噪效果对比,证明了EMD-JADE算法降噪效果优于传统的EMD算法,能够有效避免EMD有时因为发生模态混叠而造成降噪效果不佳的状况;EMD-JADE算法重点解决了JADE算法只能用试配方法来构造虚拟噪声去匹配真实噪声用来降噪的问题,仿真及实测信号分析结果证明了EMD-JADE算法适用于汽车变速器的齿轮故障诊断.

[1] 唐贵基,叶进生,胡爱军.基于谐波小波包的微弱信号的频域提取[J].现代电子技术,2009,296(9):156-159. TANG Guiji, YE Jinsheng, HU Aijun. Extracting weak signal in the frequency domain based on the harmonic wavelet packets[J].Modern Electronic Technology,2009,296(9):156-159.

[2] 陈彦龙,张培林,吴定海,等.基于DCT的微弱信号提取和识别[J].噪声与振动控制,2012(1):133-136. CHEN Yanlong, ZHANG Peilin, WU Dinghai, et al. Weak signal extraction and recognition based on DCT[J].Noise and Vibration Control,2012(1):133-136.

[3] 朱世欣,谯自健,杨智刚.基于SVD-EMD的有效微弱信号

提取算法[J].测控技术,2014,33(11):60-62.

ZHU Shixin, QIAO Zijian, YANG Zhigang. Effective weak signalextraction algorithm based on SVD-EMD[J].Mesurement & Control Technology,2014,33(11):60-62.

[4] 周昊,陈长征,周勃,等.大型风力机主轴承故障信号提取方法[J].沈阳工业大学学报,2015,37(1):22-27. ZHOU Hao, CHEN Changzhen, ZHOU Bo, et al. Lord bearing fault signal extraction method of large wind machine[J].Journal of Shenyang University of Technology,2015,37(1):22-27.

[5] JUTTEN C, HERAULT J. Blind separation of sources[J].Signal Processing,1991,24(1):1-29.

[6] COMON P. Independent component analysis, a new concept?[J].Signal Processing,1994,36(3):287-314.

[7] CARDOSO J F, SOULOUMIAC A. Blind beamforming for non-Gaussian signals[J].Radar and Signal Processing, IEEE Proceedings F,1993,140(6):362-370.

[8] CARDOSO J F, SOULOUMIAC A. An efficient technique for blind separation of complex sources[C]//Proceedings, IEEE SP Workshop on High-Order Stat. USA :Lake Tahoe,1993:275-279.

[9] CARDOSO J F. High-order contrasts for independent component analysis[J].Neural Computation,1999,11(1):157-192.

[10] 肖瑛,殷福亮.解相关EMD:消除模态混叠的新方法[J].振动与冲击,2015,34(4):25-29. XIAO Yin, YIN Fuliang. Decorrelation EMD: a new method of eliminating modal aliasing[J].Journal of Vibration and Shock,2015,34(4):25-29.

[11] 胡爱军,孙敬敬,向玲.经验模态分解中的模态混叠问题[J].振动、测试与诊断,2011,31(4):429-434. HU Aijun, SUN Jingjing, XIANG Ling. Modal aliasing problem of empirical mode decomposition[J].Journal of Vibration, Mesurement & Diagnosis,2011,31(4):429-434.

[12] 褚福磊,彭志科,冯志鹏,等.机械故障诊断中的现代信号处理方法[M].北京:科学出版社,2009:184.

[13] PENG Z K, PETER W T, CHU F L. A comparison study of improved hilbert-huang transform and wavelet transform: application to fault diagnosis for rolling bearing[J].Mechanical Systems and Signal Processing,2005,19(5):974-988.

[14] 李欣鑫,丁康,李巍华.转速和载荷对变速器特征频率和调制边带影响的试验研究[J].振动与冲击,2006,25(增刊):512-514. LI Xinxin, DING Kang, LI Weihua. Experimental study about the influence of speed and load on the transmission characteristics frequency and the modulation sideband[J].Journal of Vibration and Shock,2006,25(suppl):512-514.

The algorithm of EMD combined with JADE and validation

WU Chao, ZHAO Jun, GUO Tiantai, LYU Chenhuan

(College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China)

Since automotive transmission gears in tough work condition were prone to failure, a method based on the combination of empirical mode decomposition (EMD) and joint approximate diagonalization eigen-decomposition (JADE) of blind source separation algorithms was put forward for gear fault diagnosis in auto transmission. First, the vibration signal was decomposed with EMD, then the intrinsic mode function was restructured according to the rule of cross-correlation, and a virtual noise signal was constructed, which was then taken as the input matrix of JADE. Then, feature signals were obtained by using the JADE algorithm, which could clearly reflect the state of the gear. Lastly, the method was applied to gear fault diagnosis in auto transmission. The simulation and experimental analysis results show that it is feasible and effective.

empirical mode decomposition; rule of cross-correlation; joint approximate diagonalization eigen-decomposition; gear fault diagnosis