消像差Offner成像光谱仪的研究进展
2015-02-26韩姗,黄元申,李柏承等
消像差Offner成像光谱仪的研究进展
韩姗,黄元申*,李柏承,张大伟,倪争技
(上海理工大学 上海市现代光学系统重点实验室, 上海 200093)
摘要:为了获得消像差Offner成像光谱仪,以三镜系统为基础综述了Offner成像光谱仪的各种消像差方法,介绍了由两块不同曲率半径凹面镜与凸面光栅构成的Offner成像光谱仪和狭缝与刻槽成不同方向的Offner成像光谱仪的消像差方法,并得到面内结构及正交结构两种成像光谱仪结构,其中正交结构在消像差方面更具优势,为获得高质量Offner成像光谱仪提供了理论基础。
关键词:光学设计;消像差结构;像差理论;Offner成像光谱仪;凸面光栅
*通讯联系人。E-mail:hyshyq@sina.com
引言
成像光谱仪是20世纪80年代以来以光谱遥感成像技术为基础发展起来的一种能同时获取物体空间和光谱信息的光学遥感仪器,具有图谱合一性。广泛应用在卫星遥感技术、林业、农业、地质、医药、军事、海洋、地质勘探、生产制造、色度学、生态学等相关领域[1-7]。而在各类型成像光谱仪中,Offner成像光谱仪因其完美的光学特性,受到了更为广泛的关注。
Offner成像光谱仪是建立在全反射式Offner两镜同心成像系统之上的,将该系统中的凸球面镜换成凸球面光栅,就得到Offner成像光谱仪结构[8]。应用Offner成像系统的成像光谱仪与原有的采用平面光栅或凹面光栅结构的成像光谱仪相比,具有明显的优点[9]。这些优点包括以下几方面:(1)具有完善成像能力,例如,一个微型Offner结构的设计方案可以使畸变小于一个像素的0.1%,而在原有的成像光谱仪中,如采用凹面光栅的Dyson结构成像光谱仪,在相同情况下能够取得的最小畸变至少是它的几十倍;(2)它的光谱性能大大超过其它类型的光谱仪,具有高的光谱和空间分辨率;(3)因为它应用的是球面反射光学元件,并采用同心结构,使得对其设计更为简单,使它很容易做成小型化和轻型化的仪器,适合空间技术的发展需要。
为获得高成像质量Offner成像光谱仪,2006年,PRIETO-BLANCO[10]等人提出了一种基于子午和弧矢聚焦曲线的简单设计方法,该方法在三元件同心和罗兰圆配置的条件下,将子午和弧矢聚焦曲线在某一中心波长下相切,使设计方法简单、迅速。随后,2007年LUCKE[11]提出了一种平面外色散的Offner光谱仪。对于一个短狭缝系统可以使色散在所谓最佳成像面(best imaging circle,BIC)附近得到好像质的光谱像。PRIETO-BLANCO[12]对这种系统进行了深入研究。在一个正交结构中,即入缝和出缝在两个互相垂直的平面内,可以实现消像散结果,获得较好的成像质量。由此看出,对于消像差Offner系统的设计具有非常重要的研究意义。
1Offner成像光谱仪光学结构
THEVENON首先提出Offner两镜同心成像系统,随后FISHER,CHRISP和MOUROULIS等人又分别对此型分光系统进行了不同的设计[13-15],使其在相关领域得到了发展。1987年KWO[16]等人提出了基于Offner成像系统的光栅成像光谱仪,这种设计在消除第3级像差方面取得了理想的效果,但要消除第5级像散则需要通过使用像差矫正光栅或者将光栅略微倾斜的方法,这就会使系统失去原有的对称性,带来彗差。
1999年CHRISP等人针对此缺点进行了改进,将大凹球面镜分成两个小凹球面镜,重新获得同心结构并采用罗兰圆配置,使得光谱成像系统更具小型化和轻量化。图1为Offner成像光谱仪结构示意图,包括一个点光源S,两个球面反射镜M1和M2,一个凸面光栅G,一个像点I。其中M1,M2和G拥有同一个球心C,即为三同心光学系统。M1,M2,G在顶点处的法线与S点共平面,光栅G的刻线方向垂直于该平面。 为方便描述,在示意图中只画出了入射主光线(波长为λ)SO1经M1反射到达O点,主光线O1O经G衍射后的M2级光到达O2点,衍射主光线OO2经m2的反射光线最后到达像平面上的I点。距离SO1,O1O,OO2,O2I以及主光线SO1,O1O,OO2的入射角、光栅G的衍射角,称为Offner成像光谱仪的结构参量。

图1 Offner成像光谱仪结构
2Offner成像光谱仪的像差理论
现有的对Offner成像光谱仪进行成像质量分析的方法主要有解析点列图理论、单光栅像差理论及应用光程函数的计算方法。1983年CHRISP[17]提出的波像差理论是第1个针对多元件光学系统的像差理论,后经LÜ[18]发展使之适应平面对称的多元件光学系统。GOTO[19]等人把这种分析方法引入光栅光学系统。以此为基础,NAMIOKA[20-21]等人建立了解析点列图理论。2006年,PRIETO-BLANCO[10]应用单光栅理论对Offner成像光谱仪的像差理论进行了分析,随后又采用类似凹面光栅几何理论[22]的方法,即通过建立任意光线的光程函数,进行幂级数展开,求解子午和弧矢聚集曲线方程的方法,得到了Offner成像光谱仪的像差理论的又一种解析方式。
2.1 应用解析点列图理论
应用解析点列图理论进行系统像差分析[23]首先要利用光线追迹方法得到系统的数值模型, 然后运用级数展开方法, 建立起系统的3 阶解析模型,该模型给出了系统像差系数并可用于计算系统点列图的解析表达式。
对给定的Offner成像光谱仪结构,进行光线追迹,并对其建立解析模型,得到像平面上点I(0,Y,Z)的解析表达式[23]如下式所示:

上式是Offner成像光谱仪的解析模型,也是用于生成系统点列图的解析表达式,其中模型参量Eijk和Fijk(其中i,j,k分别对应式中的0,1,2)是系统的像差系数,是系统参量的函数,w1和l1分别表示的是物点在M1上投射点的(y,z)坐标。可通过该解析模型生成的系统点列图,较准确地分析系统的成像质量。
正如虚宁寺管委会的李副主任所说:“对于我们而言,构建和谐社会的大目标,就要从人与人之间互相关怀的点滴开始做起。”
2.2 单光栅像差理论
PRIETO-BLANCO等人于2006年提出了基于单光栅像差理论的解析方法,因为通过对光栅衍射特性的分析可以类推到Offner成像光谱仪结构中。又因为由凹面镜出射的光,再经凸面光栅衍射后的情况,可以等同于由凹面镜反射后的光,在凸面光栅上成虚像,再把此虚像当成实物点经一凹面光栅后进行衍射的情形,因此,通过描绘凹面光栅衍射过程,就可以将相关理论应用到凸面光栅。因此,对于Offner成像光谱仪像差理论的分析,大都应用的是此理论。
2.2.1子午弧矢聚焦曲线相交该方法是基于单光栅像差理论,由PRIETO-BLANCO等人于2006年提出的[10],在保证罗兰圆配置的条件下,使子午和弧矢聚焦曲线在某一波长处相交或相切,来消除中心波长的像散。
像散产生的原因为子午像点与弧矢像点之间存在的距离,因此,要想获得零像散点,就要求这个距离值为0,即通过计算所对应的物像位置关系,就可以来得到消像散像。图2为成像光谱仪简化结构图,Is和Im分别表示的是物点所成的弧矢像点和子午像点,C为系统的公共球心。通过像散点的物理含义(即Is与Im之间的距离),可以将其表示为:

式中,φm′和φs′分别为子午与弧矢像与系统x轴所成夹角。因此,当满足φs′=φm′时,I(IsIm)就为0,即得到消像散点。然而,与上式对应的只有某一特定波长λ,此时,子午像与弧矢像相交。另外一种设计就是使子午像与弧矢像在λ处相切,来达到消像差的目的。

图2 成像光谱仪简化结构图
2.2.2凹面光栅衍射理论由于凹面光栅的衍射理论,完全可以应用到凸面光栅理论中来,因此,PRIETO-BLANCO等人于2009年应用波动光学原理对凹面光栅的成像特点进行了详尽的分析[24]。该研究过程中得到的表达式更为简单,便于设计,能更好地应用到Offner成像光谱仪的研究工作中。图3是该理论的原理图。图中,A为点光源,其对应的极坐标为(r0,θ0,α0),B为点光源A所成的像,其衍射级次为m,B的坐标为(r1,θ1,α1)。其中,r0,r1分别表示物点A与像点B距离光栅顶点的距离,θ0和θ1分别是参考光线的入射角和衍射角,而α0和α1是入射平面和衍射平面与x-z平面所成的角度。
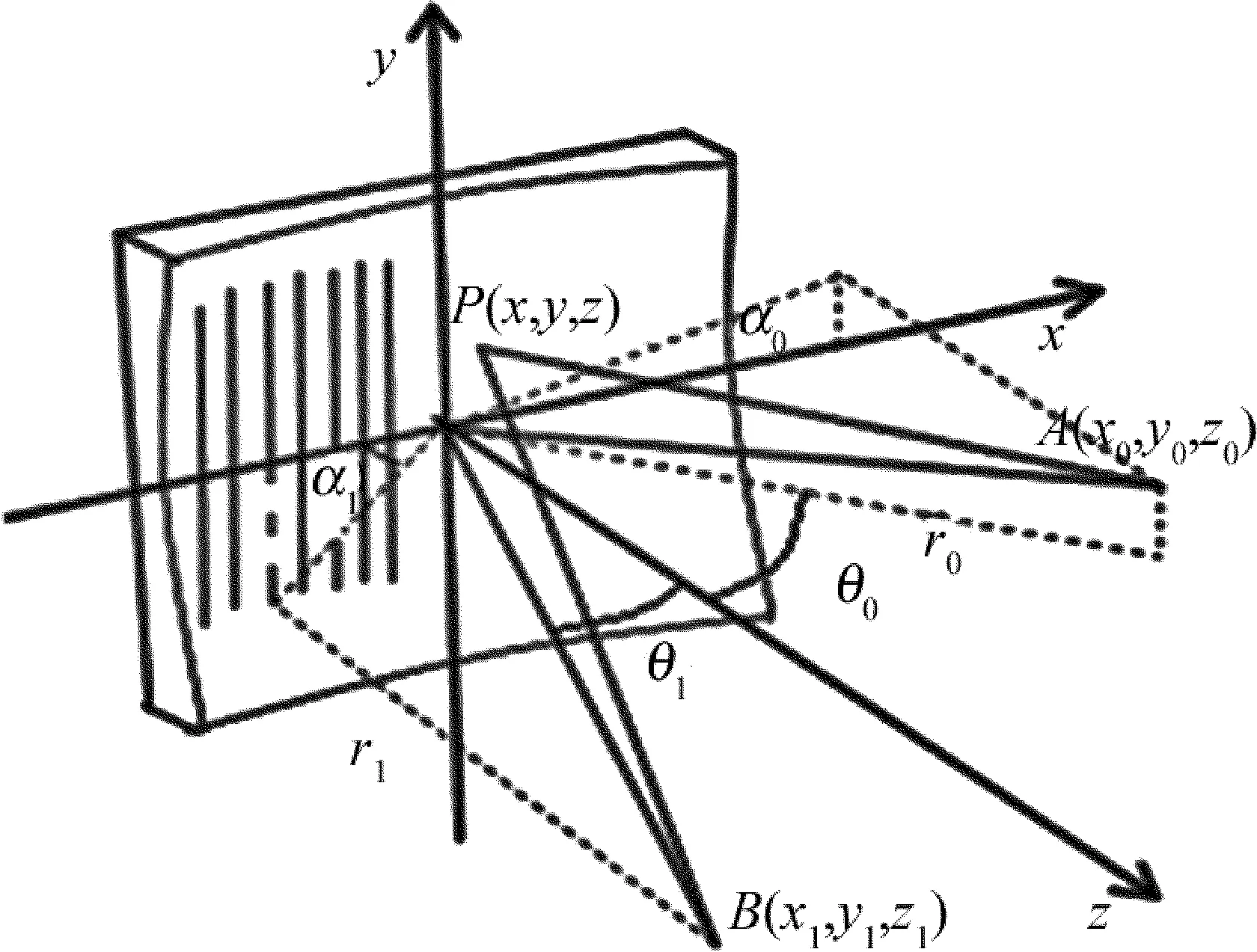
图3 凹面光栅衍射原理图
首先,根据凹面光栅成像理论,定义光程函数为从A点到B点的光程(与光栅的交点为P)加上由光栅周期结构所决定的相位变化。即:

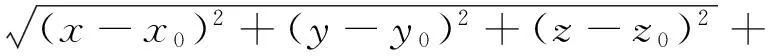

式中,d表示光栅常数。对J进行泰勒级数展开,以及根据费马原理可以得到:


进一步求解J的2阶导数,并通过代数计算,得到消像散成像条件,如下式所示:



r0sin2θ1=r1sin2θ0=

再由已知条件得出:


这样,就可以由(6)式、(7)式得出物像距离关系为:



2.3 基于光程函数分析方法
2010年,GONZEZ等人针对Offner成像光谱仪结构,应用光程函数(lightpathfunction,LPF)解析的方法对该结构进行了分析[25]。通过对LPF的计算可以对任意物像位置的成像特点进行研究,并且可以避开由衍射光栅产生的中间像点所带来的复杂的解析过程。LPF的级数展开式决定了成像光谱的像差大小,因此可以以此来获得消像差的光谱仪结构。
图4即为Offner成像光谱仪结构图,这里光程定义为经光栅衍射之前的光程L以及经光栅衍射之后的光程L′再加上光栅的刻线函数,因此可以得出:
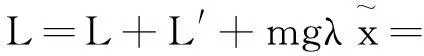

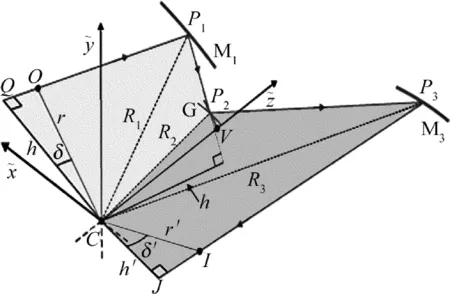
图4 LPF理论原理图

3两种结构介绍
针对第2节中对Offner成像光谱仪像差理论的分析,可以得出存在两种特殊的结构,使成像光谱仪具有好的成像质量,下面,就对这两种结构在消像差方面贡献叙述如下。
3.1 面内结构
如第2.2.2节中所述,当α1=α0=0时,对应的是面内结构,其结构参量符合以下两等式:


其中与(13)式对应的是子午成像面,与(14)式对应的是弧矢成像面,在0级衍射或镜面反射的情况下,(14)式可以叙述为系统的物点、反射镜的曲率中心、及弧矢像点处于同一直线上。
对于面内结构的应用,一般采用的是罗兰圆设计[14],即入射狭缝的中心位于第一凹面反射镜的罗兰圆上。由理论计算可知,此时,在不考虑入射波长的情况下,物点O所成的子午像也位于该罗兰圆上,并且,此时子午像具有无彗差的特点。根据(13)式还可以计算出:如果物点与光栅顶点的距离r0=Rcosθ0,那么相应的像距(像点到光栅顶点的距离)r1=Rcosθ1。而物点O对应的弧矢像点就不在此罗兰圆上,这就使得子午像面的像散成为主要像差。
3.2 正交结构



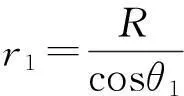
由第2.2.2节中叙述可知,正交结构还可以使在特定波长λq条件下,入射狭缝的中点O所成的像具有无像散的特点。其基本思想是得到从凸面镜出射的两虚像点位置,然后,这两个像点经光栅再次成像在垂直平面上,由此获得的像点通过三镜(M3)再成像的特性同一镜(M1)的情况相同,因此,最后两像点在I点处重合。也可以说,存在一物点O的位置,可以使物点到一镜的距离等于从最终像点I到三镜的距离。只要找到该物点的位置就可以对Offner成像光谱仪进行设计了。
通过上述讨论可以发现,正交结构的Offner成像光谱仪在消像差方面更具有优势,该结构在利用同心结构无彗差特性的同时,找到了一物像点的对应位置,使得所成像点具有无像散的特点,这对于消像差Offner成像光谱仪的设计提供了帮助。
4总结与展望
随着空间技术的发展,具有高成像质量的光谱仪器越来越受到人们的关注,对其研究也逐渐深入。通过解析点列图理论、单光栅像差理论及光程函数分析方法对Offner成像光谱仪像差理论进行分析,得到两种结构,可以在一定程度上减小像差,即面内结构及正交结构,可为Offner成像光谱仪的设计提供帮助。但目前,对消像差Offner成像光谱仪的优化设计,大多是对等间距刻线的凸面光栅,并在特定波长下,采用点光源代替的方法进行讨论的,而且主要消除的像差是像散项,并没有对其它像差进行讨论。因此,针对不同刻线分布的凸面光栅Offner成像光谱仪的成像特点分析,以及对减小Offner成像光谱仪其余像差的优化设计以提高其成像质量,将是未来的研究趋势。
参考文献
[1]ZHU Sh B, JI Y Q, GONG G B,etal. Optical design of prism-grating-prism imaging spectrometers[J]. Acta Photonica Sinica, 2009, 38(9): 2270-2273(in Chinese).
[2]GAT N.Imaging spectroscopy using tunable filter: a review.Proceedings of the SPIE,2000,4056:50-64.
[3]XIE H B,ZHU X Ch, LI E Y,etal. An emitting optical system design for laser panorama detection[J]. Laser Technology,2013, 37(2): 191-194(in Chinese).
[4]HUANG Y Sh,CHEN J B.Fourier analysis of Offner imaging spectrometer composed of a convex grating[J].Optical Instruments,2007,29(6): 40-43(in Chinese).
[5]TONG Y J,WU G,ZHOU Q,etal. Design method of offner-type imaging spectrometer[J].Acta Optica Sinica,2010,30(4): 1148-1152(in Chinese).
[6]HUANG Y Sh, NI Zh J, ZHUANG S L. Research of the conentric optical system of grating spectrometers[J]. Optical Instruments,2005,27(6):38-42(in Chinese).
[7]QU W J,XIE H,HU Q G,etal. Optical filtering character -ristics for Gaussian beam passing through of diffractive gratings[J].Laser Technology, 2012,36(4): 540-543(in Chinese).
[8]MERTZ L. Concentric spectrographs [J]. Applied Optics,1977,16(12):3122-3124.
[9]HUANG Y Sh,NI Zh J. Research of the concentric three-reflection optical system[J].Optical Instruments,2005,27(2):42-46(in Chinese).
[10]PRIETO-BLANCO X, MONTERO-ORILLE C, COUCE B,etal.Analytical design of an Offner imaging spectrometer[J].Optics Express,2006, 14(20): 9156-9168.
[11]LUCKE R L.Out-of-plane dispersion in an Offner spectrometer.Optical Engineering,2007,46(7):073004.
[12]PRIETO-BLANCO X, MONTERO-ORILLE C, GONZ.The Offner imaging spectrometer in quadrature[J].Optics Express, 2010,18(12): 12756-12769.
[13]FISHER J, ANTONIADES J. Hyperspectral imaging sensor for the coastal environment.Proceedings of the SPIE,1998, 3482: 179-186.
[14]CHRISP M P. Convex diffraction grating imaging spectrometer: US, 5880834 [P] . 1999-05-09.
[15]MOUROULIS P. Compact infrared spectrometers[J].Proceedings of the SPIE,2009,7298:729803.
[16]KWO D, LAWRENCE G, CHRISP M. Design of a grating spectrometer from a 1∶1 Offner mirror system[J].Proceedings of the SPIE,1987,818: 275-279.
[17]CHRISP M P. Aberrations of holographic toroidal grating systems[J]. Applied Optics,1983,22(10):1508-1518.
[18]LÜ L J. Aberration theory of plane symmetric grating systems[J].Synchrotron Radiation,2008,15(4):399-410.
[19]GOTO K, KUROSAKI T. Canonical formation for the geometrical optics of concave gratings[J].Journal of the Optical Society of America,1993,A10(3):452- 465.
[20]NAMIOKA T, KOIKE M, CONTENT D. Geometric theory of the ellipsoidal grating[J].Applied Optics,1994, 33(31): 7261- 7274.
[21]MASUI S, NAMIOKA T.Geometric aberration theory of double element opticalsystems[J]. Journal of the Optical Society of America,1999,A16(9):2253-2268.
[22]PRIETOB-LANCO X, GONZEZ H, de la FUENTE R.Off-plane anastigmatic imaging in Offner spectrometer[J]. Journal of the Optical Society of America,2011,A28(11):2232-2239.
[23]LIU H G,WU G, LING Q,etal. Modelling of Offner imaging spectrometers and aberration analysis[J].Acta Optica Sinica,2011, 31(3):0322001.
[24]PRIETO-BLANCO X,MONTERO-ORILLE C, GONZImaging with classical spherical diffraction grating : the quadrature configuration[J]. Journal of the Optical Society of America,2009,A26(11):2400-2409.
Progress of Offner imaging spectrometers for eliminating aberration
HANShan,HUANGYuanshen,LIBaicheng,ZHANGDawei,NIZhengji
(Shanghai Key Laboratory of Modern Optical System, University of Shanghai for Science and Technology, Shanghai 200093, China )
Abstract:Research background and optical structure of an Offner imaging spectrometer were introduced. Aberration of the Offner imaging spectrometer was analyzed by analytical point row graph theory, single grating aberration theory and light path function analysis method respectively. Two special structures (surface inner structure and orthogonal structure) were put forward, which can allow imaging spectrometer with better image quality. It is the research trend to improve the image quality of an imaging spectrometer in the future.
Key words:optical design; eliminating aberration structure; aberration theory; Offner imaging spectrometer; convex grating
收稿日期:2013-12-04;收到修改稿日期:2013-12-16
作者简介:韩姗(1989-),女,硕士研究生,主要从事凸面衍射光栅的研究。
基金项目:国家自然科学基金资助项目(61205156;11105149);国家重大科学仪器设备开发专项资助项目(2011YQ15004002;2011YQ15004004);上海市教委曙光资助项目(11SG44);上海市科技委科研计划资助项目(11DZ2290301);上海市研究生创新基金资助项目(JWCXSL1302)
中图分类号:TH744.1
文献标志码:A
doi:10.7510/jgjs.issn.1001-3806.2015.01.007
文章编号:1001-3806(2015)01-0033-06
