非线性囚禁离子振动模式互关联函数的研究
2015-03-18王中结
王中结,方 旭
(安徽师范大学物理与电子信息学院,芜湖241000)
引 言
近年来,激光束操控囚禁离子的研究已成为非常活跃的研究领域。囚禁离子系统不仅在工程的量子态方面是非常重要的[1-2],而且在诸如量子隐形传态和量子计算中有重要的应用价值[3-5]。在Lamb-Dicke极限下,囚禁离子与经典驻波光场的相互作用通常是由类似于腔量子电动力学的Jaynes-Cummings(J-C)模型描述。在J-C模型基础上,为制备各种非经典状态,人们提出了许多方案,例如Fock态的制备[6]、纠缠态的制备[7]、压缩相干态的制备[8]、纠缠态的制备[9]、激发薛定谔猫态的制备[10]、簇态的制备[11]等。但是,在远离 Lamb-Dicke极限下,囚禁离子与经典驻波光场的相互作用必须由非线性J-C模型来描述。近来,在非线性J-C模型基础上,人们提出了制备非线性相干态的方法[12],并对二能级囚禁离子的量子动力学进行了研究[13-15],如参考文献[13]中,作者研究了二能级囚禁离子的非线性J-C模型,分析了非线性对离子布居数的影响。然而,在关于囚禁离子的非线性J-C模型的研究中,人们大多集中考虑二能级囚禁离子与驻波激光束的相互作用。
本文中研究了单个三能级2维囚禁离子与经典驻波激光场的相互作用,得到了这个非线性J-C模型的严格解,数值分析了2维囚禁离子的振动运动之间的交叉关联效应。结果表明,非线性参量对交叉关联效应有明显地影响。
1 模型及其演化算符
考虑囚禁在一个2维简谐势阱中单个三能级离子,与两束分别沿x和y方向的驻波激光场相互作用,一束激光场的频率为 ωlaser,1,另一束频率为ωlaser,2。囚禁离子由两个基态和一个激发态组成,基态和〉的能量分别为 ω1和 ω2,激发态的能量为 ω3,如图1所示。
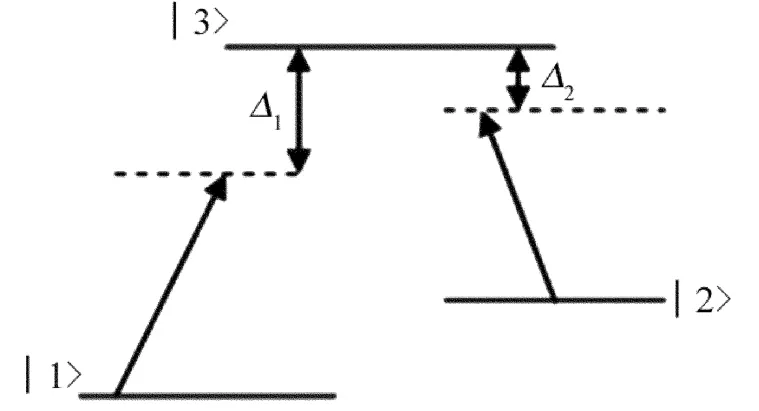
Fig.1 Level scheme of the trapped ion interacting with two standing wave laser fields
随着应用的旋转波近似,系统的哈密顿量为(令=1):

式中,ai(a+i)(i=1,2)表示囚禁离子沿x和y方向的质心振动运动的湮灭(产生)算符,νi是囚禁频率,φi(i=1,2)是驻波激光场的相位(沿x和y方向),gi是耦合常数,ηi=ki是Lamb-Dick参量,m是囚禁离子的质量,ki是驻波激光场的波数。
在下面的计算中,假定 g1=g2=g,φ1=φ2=φ。在相互作用图像中,相互作用哈密顿可表示为:

式中,Δ1= ω3- ω1- ωlaser,1,Δ1= ω3- ω2- ωlaser,2。为计算方便起见,令 Δ1=ν1,Δ2=ν2。应用下列公式:

其中,

容易证明Aj和A+j算符满足下列的对易关系:

式中,δij=1(i=j),δij=0(i≠j)。应当指出哈密顿量(4)式描述了一个三能级2维囚禁离子与两束经典驻波激光场相互作用的非线性模型,并对任意值的Lamb-Dicke参量η1和η2都有效。
在原子态表象中,推导由哈密顿(4)式确定的演化算符UI=e-iHit的矩阵元,结果如下:
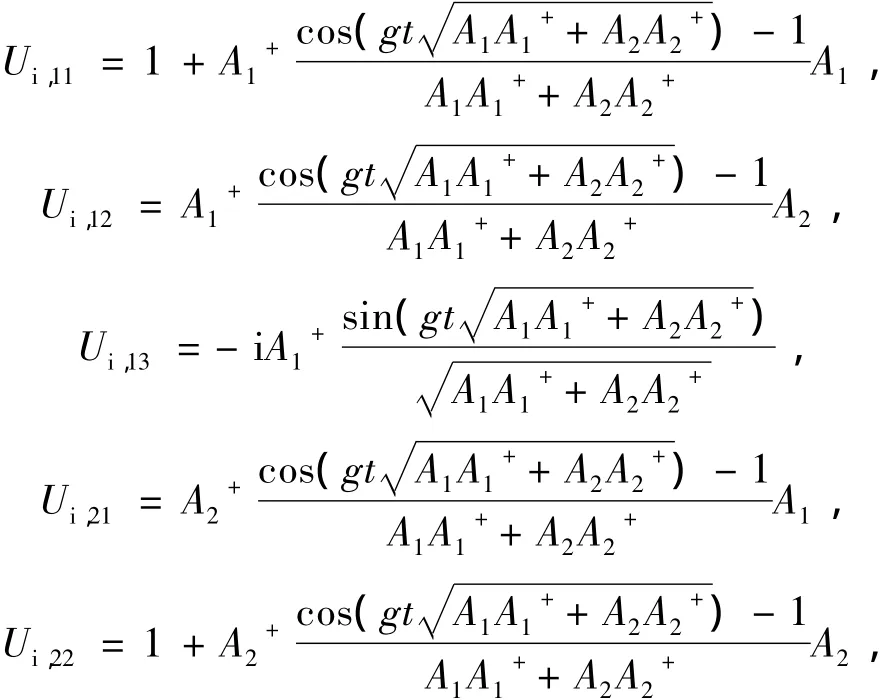
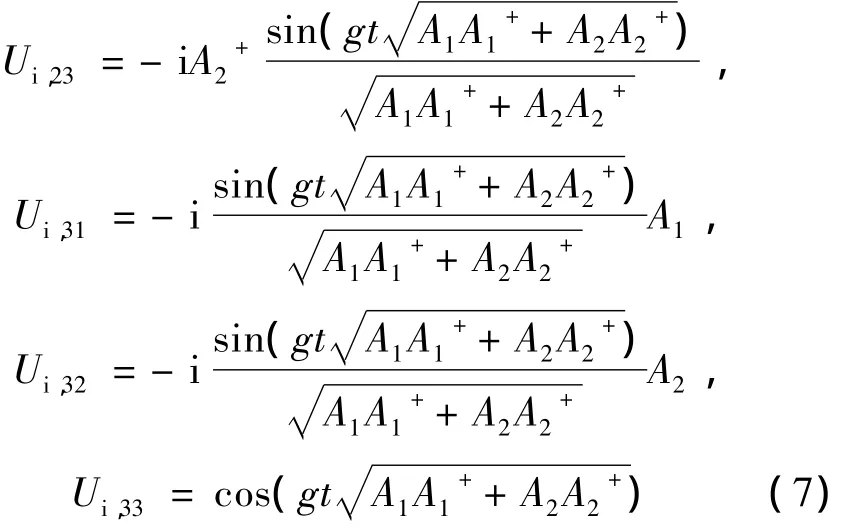
2 二模交叉关联效应
在这一节中,研究囚禁离子的沿x和y方向的振动运动之间的交叉关联效应。归一化的二模交叉关联函数定义如下:

如果Ga1a2<1,就说模式a1和模式a2是反关联的,如果 Ga1a2>1,就说两者是关联的,即囚禁离子的振动运动具有非经典的性质。为了数值计算交叉关联函数,首先假定囚禁离子初始处在激发态3〉,沿x和y方向的质心振动运动分别处在相干态

式中,Fn为算符a1和a2的本征值。应用(7)式,容易计算囚禁离子任意时刻t的态矢为:

应用(10)式,可以计算(8)式各力学量的期望值为:


Fig.2 Cross-correlation function Ga1a2versus dimensionless time τ=gt with initial average quantum number α 2=1.0,φ = π/2 and various parameters η1,η2
将(11)式代入(8)式,可得交叉关联函数Ga1a2随时间的变化。定义无量纲时间τ=gt,画出Ga1a2在不同的Lamb-Dicke参量条件下随无量纲时间的变化曲线,如图2所示。从图2中可以看出,在初始平均量子数=1.0情形下,交叉关联函数Ga1a2在某些时段对于任意的Lamb-Dicke参量都小于1,这表明模式a1和a2之间存在反关联。这种反关联效应容易受Lamb-Dicke参量η1和η2的影响。随着η1和η2的增大,反关联效应得到增强。然而,进一步增大η1和η2,反关联效应反而减弱。这说明Lamb-Dicke参量对反关联效应的影响是复杂的。另一方面,交叉关联函数Ga1a2在某些时段对于任意的Lamb-Dicke参量都大于1,这表明模式a1和a2之间存在关联,即存在非经典效应。Lamb-Dicke参量对这种关联效应有明显的影响。图2表明,Lamb-Dicke参量η1和η2越大,两模间的关联效应越强。作者进一步研究了初始平均量子数对关联效应的影响,如图3和图4所示。发现随着初始平均量子数的增大,反关联效应将减弱直至消失。
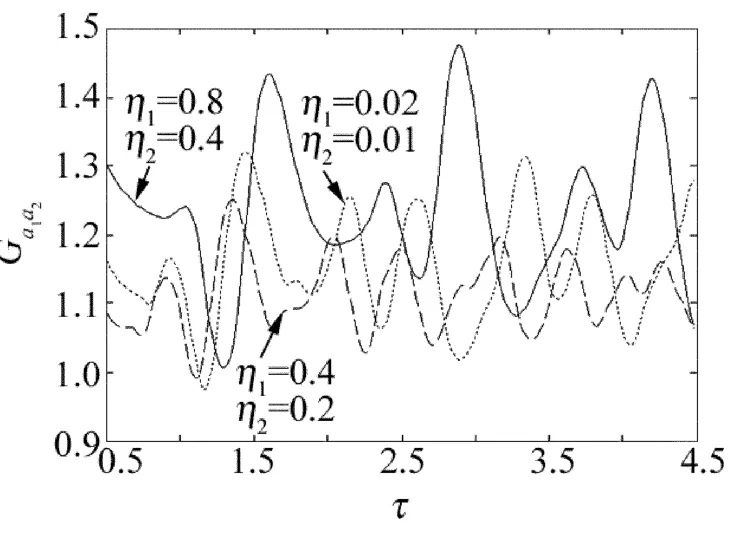
Fig.3 Cross-correlation function Ga1a2versus dimensionless time τ=gt with initial average quantum number =2.0,φ = π/2 and various parameters η1,η2
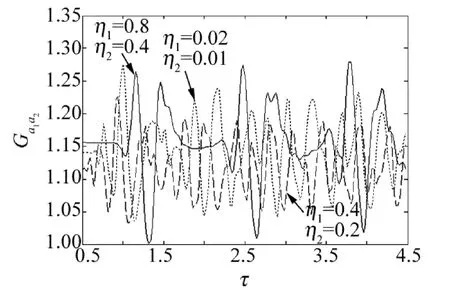
Fig.4 Cross-correlation function Ga1a2versus dimensionless time τ=gt with the initial average quantum number =5.0,φ = π/2 and the various parameters η1,η2
3 讨论
下面提出一个可能的实验构型[16]。将一个40Ca+置于一个强射频的Pauli势阱中,离子在势阱中沿 x和 y方向的振荡频率取为 ν1=ν2≈70.3MHz,并由沿x和y方向的驻波激光场驱动。离子采用受激Raman激光冷却技术。离子的两个能级基态2S1/2和亚稳态2D5/2(寿命约1s)分别记为和,另一个能级2P1/2记为。这里,给出一个测量离子振动模式的交叉关联函数的方法。用一束与x轴成45°的方向传输的经典行波光场将囚禁离子从基态激发到高激发态,系统哈密顿为:
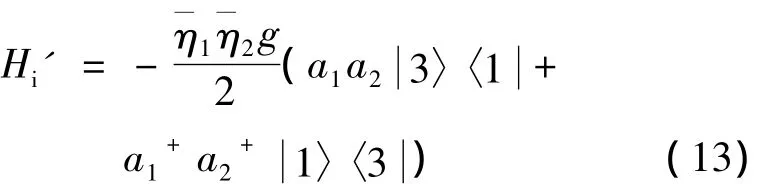
可以看出,离子从基态跃迁到高激发态的几率的时间导数正比于〈a+1a+2a1a2〉,即正比于二模交叉关联函数[17]。至此,利用荧光光谱技术可以测量离子振动模式的交叉关联函数,参见参考文献[18]。
4 结论
研究了一个2维三能级囚禁离子与两束经典驻波激光场的相互作用的非线性J-C模型。求出了这个非线性J-C模型的严格解。分析了囚禁离子的两个振动模式之间的交叉关联函数。数值计算结果表明:Lamb-Dicke参量(表征非线性效应,这个参量越大,非线性越强)对交叉关联有明显地影响;当初始平均量子数较小时,反关联效应随Lamb-Dicke参量的增大先是也增大然后减弱,但是关联效应却随Lamb-Dicke参量的增大一直增强;随着初始平均量子数的增大,反关联效应会减弱直至消失。
[1] LEIBFRIED D,BLATT R,MONROE C,et al.Quantum dynamics of single trapped ions[J].Reviews of Modern Physics,2003,75(1):281-354.
[2] ROOS C,ZEIGER T,ROHDE H,et al.Quantum state engineering on an optical transition and decoherence in a Paul trap[J].Physics Review Letters,1999,83(23):4713.
[3] BARRETT M D,CHIAVERINI J,SCHAETZ T,et al.Deterministic quantum teleportation of atomic qubits[J].Nature,2004,429(6993):737-739.
[4] GARCIA-RIPOLL J J,ZOLLER P,CIRAC J I.Speed optimized two-qubit gates with laser coherent control techniques for ion trap quantum computing[J].Physics Review Letters,2003,91(15):157901-157904.
[5] DUAN L M.Scaling ion trap quantum computation through fast quantum gates[J].Physics Review Letters,2004,93(10):100502-100505.
[6] CIRAC J I,BLATT R,ZOLLER P.Nonclassical states of motion in a three-dimensional ion trap by adiabatic passage[J].Physics Review,1994,A49(5):R3174.
[7] KIRCHMAIR G,BENHELM J,ZAHRINGER F,et al.Deterministic entanglement of ions in thermal states of motion[J].New Journal of Physics,2009,11(2):023002-023022.
[8] WANG Zh J.Preparation of squeezed state and entanglement state between vibrational motion of trapped ion and light[J].Communications in Theoretical Physics,2010,54(6):1109-1110.
[9] ZHENG Sh B.Genereation of multi-mode excited coherent states for N trapped ions in strong-excitation regime[J].Communications in Theoretical Physics,2005,43(3):523.
[10] WANG Zh J,ZHANG X D,LI C.Properties and generation of photon-added Schrödinger cat states[J].Communications in Theoretical Physics,2012,57(3):459-462.
[11] WUNDERLICH H,WUNDERLICH C,SINGER K,et al.Twodimensional cluster-state preparation with linear ion traps[J].Physics Review,2009,A79(5):052324-052334.
[12] de MATOS FILHO R L,VOGEL W.Nonlinear coherent states[J].Physics Review,1996,A54(5):4560-4563.
[13] WANG Zh Q,DUAN Ch K,AN G L,Nonlinear jaynes-cummings model of a trapped ion and the evolution of the ion population inversion[J].Acat Physica Sinica,2006,55(7):3438-3442(in Chinese).
[14] YU W J,WANG J S,LIANG B L.Quantum properties of twolevel atoms interacting with nonlinear coherent states[J].Acta Physica Sinica,2012,61(6):060301(in Chinese).
[15] LI C,WANG Zh J.Amplitude-squeezed effects in nonlinear trapped model[J].Journal of Atomic and Molecular Physics,2013,30(3):435-440(in Chinese).
[16] HAFFNER H,GULDE S,RIEBE M,et al.Precision measurement and compensation of optical stark shifts for an ion-trap quantum processor[J].Physics Review Letters,2003,90(14):143602-143607.
[17] GUO G C.Quantum optics[M].Beijing:Higher Education Press,1990:76-87(in Chinese).
[18] WALTHER H.Spectroscopy of single trapped ions and applications to frequency standards and cavity quantum electrodynamics[J].Laser Physics,1999,9(1):225-233.
