布尔型贝叶斯网络参数学习

吴永广，周兴旺

(空军航空大学基础部，长春 130022)

随着互联网技术发展，大数据时代的4V特性:Volume(大量)、Velocity(高速)、Variety(多样)、Value(价值)，对海量数据处理的能力提出了更高的要求。贝叶斯网络理论的发展适应了大数据特性，它以灵活的推理能力和知识表达能力受到了学者的广泛认可。贝叶斯网络理论在人工智能、数据挖掘、统计决策、医疗诊断、专家系统、军事评估等领域［1－2］发挥重要作用。关于贝叶斯网络学习的理论和方法也不断被提出和改进来满足实际的需要:从静态贝叶斯网络发展到了动态贝叶斯网络，实时动态地分析处理数据能力不断改善［3］;从专家知识表示发展到了智能化学习算法［4］，对于知识表达也更加客观合理;从推理算法到贝叶斯分类算法也呈现了多样性的发展趋势［5］。摆脱专家知识的主观性，基于数据知识驱动下的贝叶斯网络参数学习算法将对数据挖掘、人工智能发展具有重大意义。

1 参数学习研究现状

贝叶斯网络学习算法分为结构学习和参数学习两步骤。专家构建网络模型或者结构学习是参数学习的前提和基础。参数学习依据学习的样本数据划分为完整数据下和不完整数据下的贝叶斯网络参数学习。最大似然估计算法［6］作为统计学的经典算法，它是具有理论性的点估计法，为参数学习算法奠定了基础。贝叶斯估计算法［7］以狄利克雷分布作为先验概率，这样参数θ的后验概率也服从狄利克雷分布，它将先验知识和样本数据统一起来，以共轭先验分布为前提，随着样本数据的增加而逐渐减少对先验知识的依赖。Lauriten［8］提出的基于EM算法下的可以应用于数据缺失情况下的贝叶斯网络的参数学习，它通过不断修正初始估计参数值θ来最大化似然函数或者后验概率，寻找最优参数。面向大规模数据集的贝叶斯网络参数学习算法［9］通过改进E步骤试图通过更新部分数据块的期望值来降低EM算法的计算量，同时提高计算精度。这些传统的参数学习算法都是以狄利克雷、高斯分布描述参数的分布律，且变量的参数服从同一分布，它对参数学习过于理想化，应用中的贝叶斯网络的节点分布律难以同实际相结合，制约了其在应用中的价值。

2 布尔型贝叶斯参数学习算法

布尔型网络结构下的参数学习方法在处理数据方法上有了很大改进，二进制的随机变量能够进行逻辑运算，方便了数据处理。考虑到指示变量对算法复杂度影响，引入连接树(Junction Tree)算法［10］对布尔型网络函数分解，使数据处理更加易于实现，提高了效率。通过引用布尔型网络函数，利用最大似然估计最优化参数的方法将为参数学习及其实际应用提供有力的理论支撑。

2.1 布尔型网络

网络的拓扑结构研究广泛，其中布尔型网络是指一类具有二值(True，False)节点集组成的贝叶斯网络，它继承了网络分析处理的能力，且易于计算机实现。从化学，生物，到经济计算机科学，基于布尔网络的网络应用程序可以在许多领域发现其价值［11］。Darwiche教授对布尔型贝叶斯网络推理也有深入研究，通过引入证据变量的方法对于处理布尔型贝叶斯网络具有很好的效果［12－13］。在他们研究的基础上，本文提出了针对布尔型贝叶斯网络的参数学习。

定义一个布尔型函数

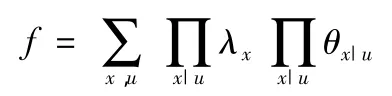
证据变量λx:对于贝叶斯网络参数X，变量λx代表事件发生的状态，为布尔型变量。引入证据变量，使证据事件同变量的状态结合，能够很好地通过线性函数表达式进行分析处理。

参数变量θx|u:对于任意的父节点u及其子节点x，以θx|u表示网络参数在父节点状态发生时的条件概率。当父节点不存在时，θx|u表示节点概率值。

如图1所示，当X和U为布尔型变量，以节点A为父节点，B和C为子节点的贝叶斯网络线性表达式为

证据事件e发生时，线性多项式f的函数值以fe表示。证据事件通过λx影响函数的取值。当变量x与证据事件e一致时，证据变量取值为1;如果变量x与证据事件对立时，证据变量取值为0;当变量x同证据事件e不存在相互影响的关系时，则证据变量以未知参数λx形式存在。

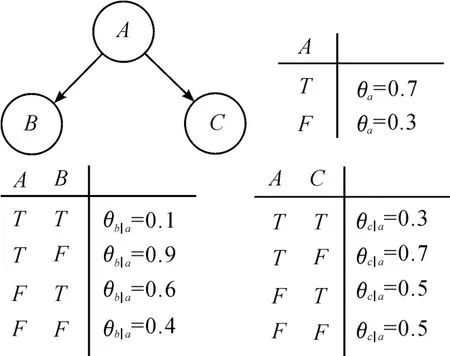
图1 布尔型网络概率表

对函数作偏微分计算

证据变量的微分特性［12］

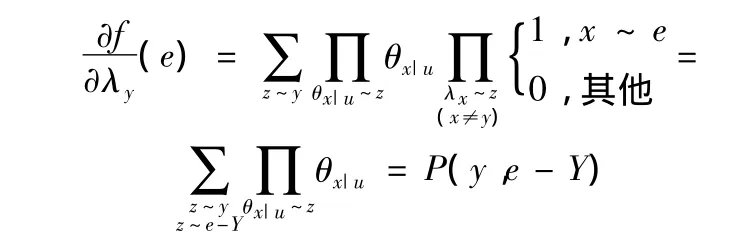
证据运算具有逻辑运算的特点，它对于处理变量关系的运算和性质有重要作用。当证据变量e实例化为b，变量x取值为时，e－X表示为时，证据变量表述为

这样，变量的概率同变量的偏微分成了互相转化的函数关系，对于计算节点联合概率，分析变量概率特性有重要作用，同时也使复杂数据处理过程变得简单化。

参数变量的微分特性，描述了节点变量的父子节点和证据的联合概率同参数变量偏微分值的等价关系，是离散变量的另一重要性质［12］

在证据e作为学习样本数据时，使得观察证据e、父节点u和子节点x的联合概率分布最大化，参数变量θx|u则为参数变量的最大似然估计。

2.2 基于连接树的网络分解

贝叶斯网络学习是一个NP-Hard难题，节点数量上升对算法性能有很大影响。为了简化算法，PL-EM算法就是对数据样本进行并行性划分来提高EM算法的效率［14］。基于人工鱼群算法的参数学习算法［15］通过人工鱼的觅食、聚群和追尾行为进行搜索，以调整人工鱼随机移动速度的方法提高了算法的收敛性能和速度。目前基于贝叶斯网络的推理研究人员提出了多种精确和近似推理算法，其中连接树(Junction Tree)算法在贝叶斯网络精确推理算法中具有计算速度快、应用广泛的特点。它能够将一个复杂的网络进行合理地分解，简化运算。

首先将贝叶斯网络进行去向处理，使网络有向图变成对应的摩尔图，实现道义化，再将道义化后的无向图转化为一个有弦图，就可以生成一棵连接树，最后根据连接树的特性及算法进行推理。

通过引入势(Potentials)函数理论［16］可以证明连接树分解算法的合理性。一组变量X上的势定义为一个函数，每个变量对应的值x称为它的实例。势函数能够将实例映射为一个非零实数，用φx表示。势可以构成向量或矩阵，也可以实现边缘化并进行乘法算法:

1)假设有一组变量Y，它的势为φy;另外有一组变量X，X⊆Y，则

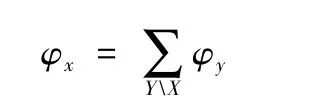
2)给定两组变量X和Y以及它们的势φx和φy，若X⊆Y，则

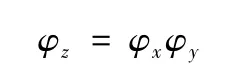
根据势函数理论，节点簇的势可用φx表示，分割集的势可用φy表示。容易证明贝叶斯网络的联合概率分布可以表示为［12］

2.3 基于最大似然估计参数算法

Spiegelhalter于1992年将最大似然估计(maximum likelihood estimation，MLE)方法成功应用于参数学习，以数据集中的变量状态影响参数的取值。最大似然估计方法就是基于实例化参数变量思想，实现最大似然化目标函数。

选取观测数据集 D=(d1，d2，d3，…，dn)，每个观测数据是一个样本点，表示贝叶斯网络中各节点的观测值。参数θs表示待学习的参数变量，以向量形式表示。参数学习是基于贝叶斯网络结构已知的情况下进行(见图2)，以G表示网络结构。最大似然估计在参数学习中应用表述如下

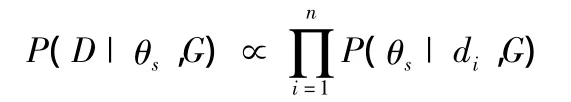
布尔函数是以线性多参数表达式形式存在，在计算过程中引入了n个指示变量，在方便数据处理的同时，也增加了算法的复杂度。根据布尔函数表达式f可知，求积项数目可以表示为O(2n)，求和项数目以指数阶O(2n)上升。当节点数上升时，线性表达函数复杂度以指数形式增加，导致参数θs维度上升，算法的效率在不断下降，甚至参数学习无法收敛到一个最优解。引入连接树算法对于复杂贝叶斯网络的处理意义重大，它合理地分解网络，能够除去不相关的状态变量对参数学习的影响。

图3是图2所对应的连接树，图3中的椭圆代表连接树的节点Ci，节点里的一组变量构成一个节点簇，方框代表节点之间的分割集。该连接树具有以下属性［16］:

1)任意两相邻节点Ci和Cj之间的边Tij对应节点集Ci∩Cj，并称 Tij为 Ci和 Cj之间的分割集。

2)连接树中任意两节点Ci和Cj之间的路径上的每条边和节点对应的变量集都包含Ci∩Cj。

将数据集合D划分为不同的证据集合，按照证据变量取值是否相同进行分类，D=(e1，e2，e3，…en)。连接树分解后的贝叶斯网络以节点簇和分割集为单元进行参数学习。通过比较网络示意图和连接树，可以发现证据集e的数目上升，证据e维度在下降。根据不同证据集合的相关性可知

对于各证据集，证据事件发生的可能性是不相同的，使所有证据发生的可能性都最大化是不合理的。引入线性权重向量 w=(w1，w2，w3，…wn)，wi=nei/ND来描述不同证据在似然函数中的重要性，可以解决证据变量的相关性问题。理想参数θs能够使函数wP(x，u，e)的取值最大化，根据最大似然函数可知，使wP(x，u，e)函数取极大值下的参数˜θs≈θs。

图2 贝叶斯网络

图3 连接树

当数据D以证据形式存在时，P(D)作为一个常量，P(θ)由参数决定，在没有先验知识的情况下，不同参数θ发生概率是未知的，P(θ)假定为一个未知的常量，引入贝叶斯定理

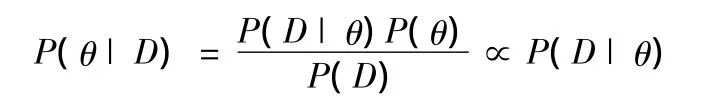
由上式可知

结合公式最优化wP(x，u，e)

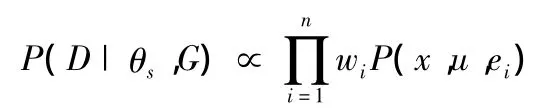
似然函数取对数处理，得到的是参数学习对数似然函数，表示如下

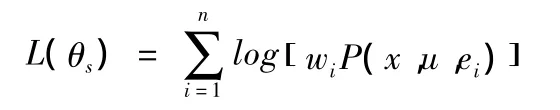
通过计算获取对数似然函数极值，找到满足条件的参数

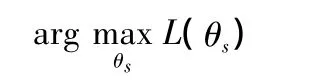
极大似然估计，在统计学中有着重要的应用，它是一种重要的参数学习方法。在离散变量概率学习中，它通过选取合适的似然函数，能够快速有效地实现参数学习。极大似然估计作为一种依赖粗略数学期望的算法，在实际中已广泛应用。在工程应用领域中，有些样本的概率是不得而知的，需要通过若干重复实验的方法获取样本数据，依据这些数据，推理出这些条件概率参数值，极大似然方法就建立在这个基础上的。如果某个参数能够最大化样本数据发生概率，忽略噪声对数据影响，它是基于已获得的数据知识下的最真实值。

3 结论

布尔型贝叶斯网络参数学习算法是基于似然函数估计的方法，引入证据的方法处理数据行之有效，它以优化线性多元函数的方式最优化参数，对于参数学习在应用中推广有很大价值。连接树的算法能够合理分解降低学习未知参数变量的维度，提高似然函数算法的性能。但算法局限于布尔型网络在一定程度下影响其应用范围，下一步将重点使算法推广到多值变量的处理中。

［1］ Julia Flores M，Nicholson A E，Brunskill A，et al.Incorporating expert knowledge when learning Bayesian network structure:a medical case study［J］.Artificial intelligence in medicine，2011，53(3):181 －204.

［2］ Park C Y，Laskey K B，Costa P C G，et al.Multi-Entity Bayesian Networks Learning In Predictive Situation Awareness［C］//Proceedings of the 18th International Command and Control Technology and Research Symposium.［S.l.］:［s.n.］，2013.

［3］ 黄世强，高晓光，任佳.DDBN的无人机决策推理模型参数学习［J］.火力与指挥控制，2013，38(1):26 －29.

［4］ Masegosa A R，Moral S.An interactive approach for Bayesian network learning using domain expert knowledge［J］.International Journal of Approximate Reasoning，2013，54(8):1168－1181.

［5］ Ngai E W T，Hu Y，Wong Y H，et al.The application of data mining techniques in financial fraud detection:A classification framework and an academic review of literature［J］.Decision Support Systems，2011，50(3):559 －569.

［6］ Spiegelhalter D J，Dawid A P，Lauritzen S L，et al.Bayesian analysis in expert systems［J］.Statistical science，1993，8(3):219－247.

［7］ Heckerman D.A tutorial on learning with Bayesian networks［M］.US:Springer Netherlands，1998.

［8］ Lauritzen S L.The EM algorithm for graphical association models with missing data［J］.Computational Statistics ＆Data Analysis，1995，19(2):191 －201.

［9］ 张少中，章锦文，张志勇，等.面向大规模数据集的贝叶斯网络参数学习算法［J］.计算机应用，2006.26(7):1690－1692.

［10］ Jensen F，Jensen F V，Dittmer S L.From influence diagrams to junction trees［C］//Proceedings of the Tenth international conference on Uncertainty in artificial intelligence.Morgan Kaufmann Publishers Inc.，1994:367 －373.

［11］ Shmulevich I，Kauffman S A.Activities and sensitivities in Boolean network models［J］.Physical Review Letters，2004，93(4):048701.

［12］ Darwiche A.A differential approach to inference in Bayesian networks［J］.Journal of the ACM(JACM)，2003，50(3):280－305.

［13］ Van den Broeck G，Darwiche A.On the complexity and approximation of binary evidence in lifted inference［C］//Advances in Neural Information Processing Systems.［S.l.］:［s.n.］，2013:2868 －2876.

［14］俞奎，王浩，姚宏亮，等.并行的贝叶斯网络参数学习算法［J］.小型微型计算机系统，2007，28(11):1972 －1975.

［15］王艳，郭军.基于人工鱼群算法的贝叶斯网络参数学习方法［J］.计算机仿，2011，29(1):185 －188.

［16］史志富，张安.贝叶斯网络理论及其在军事系统中的应用［M］.北京:国防工业出版社，2012:83－97.

(责任编辑蒲 东)