地基雷达探测临近空间高超声速目标优化部署方法*
2015-02-25肖松,谭贤四,王红等
地基雷达探测临近空间高超声速目标优化部署方法*
肖松,谭贤四,王红,汪毅
(空军预警学院,湖北 武汉430019)
摘要:为提高地基雷达对临近空间高超声速目标的探测能力,探讨了一种实用高效的地基雷达优化部署方法,对地基雷达探测临近空间高超声速目标的难点和数学模型进行了分析,提出了地基雷达探测临近空间高超声速目标的部署原则和量化指标,建立了地基雷达优化部署模型,并进行了信息素引导性控制的蚁群算法设计。仿真结果表明,该方法可实现多种程式地基雷达的优化部署,提高了地基雷达优化部署效率和可操作性,为地基雷达探测临近空间高超声速目标的优化部署提供了一种新思路。
关键词:优化部署;地基雷达;临近空间;高超声速;蚁群算法;探测
临近空间高超声速飞行器具有高高空、超高速、高机动和远距离精确打击等特性[1-2],可用于天地往返运输系统及远程精确打击系统[3],这给防空预警系统提出了新的严峻挑战[4]。如何优化部署地基雷达,提高雷达探测此类目标的效能,满足最低保障能力指标和构成最大保障能力探测网络,实现雷达资源优化配置,是当前亟待解决的问题。
针对地基雷达探测常规目标优化部署方法的研究较多[5],但是,针对临近空间高超声速目标的地基雷达优化部署方法还未见报道。文献[6]在充分考虑雷达部署的各种限制条件基础上,采用遗传算法,通过染色体群世代更迭,使部署接近最优(次优)解;文献[7]建立了环形、直线和扇形3种最优部署模型,采用完全枚举法、黄金分割法
和坐标轮换法求出最优解;文献[8]针对防区内分散于不同位置且重要度不同的责任区,基于NSGA-Ⅱ算法进行多目标优化,实现全方位全纵深的雷达部署;文献[9]通过建立目标优化函数和利用结构演变更新青蛙位置,实现组网雷达的优化部署。上述方法都是基于一定原理,对目标进行搜索,通常适用于大量部署方案中的寻优过程,针对性强,而难以满足雷达探测临近空间高超声速目标时,发现距离远、连续稳定跟踪时间长和衔接高度特殊等需求。鉴于此,结合临近空间高超声速目标特性和地基雷达部署原则,拟提出地基雷达探测临近空间高超声速目标的约束条件并建立优化部署数学模型,设计一种基于改进蚁群算法的优化部署方法,为临近空间预警系统中地基雷达优化部署提供理论支撑。
1问题描述
1.1 地基雷达探测临近空间高超声速目标
雷达天线架设高度以及目标飞行高度与雷达直视距离之间的关系如图1所示。
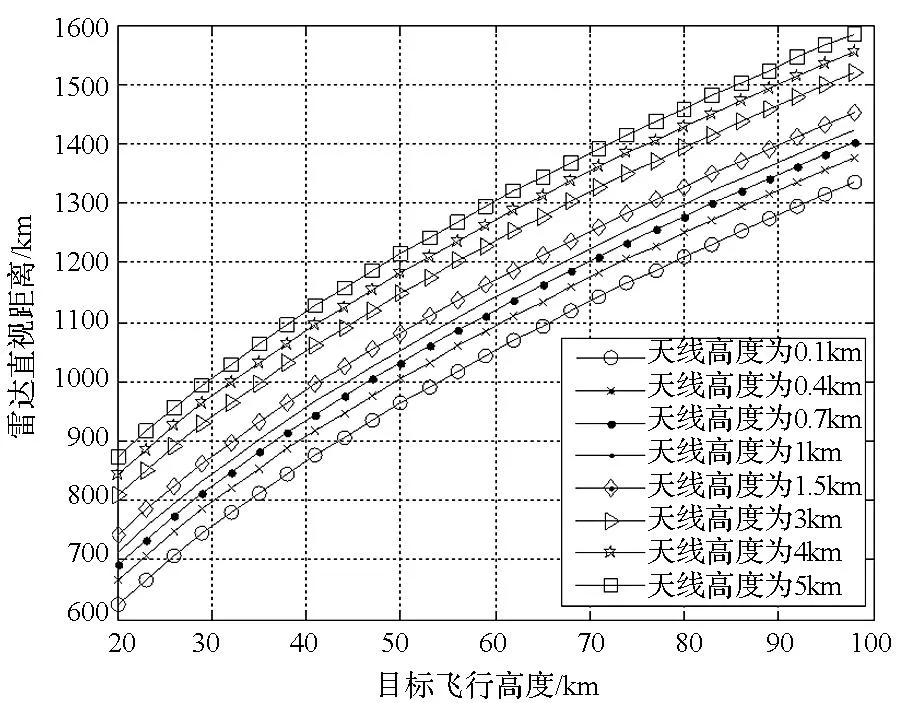
图1 雷达直视距离与目标高度关系Fig.1 Relationship of radar direct-viewdistance and target height
从图1中可以看出,理想情况下,对于飞行高度为20km的目标,地基雷达天线架高为1.0km时,地基雷达直视距离只有约700km。所以,对于飞行距离可以达到几千公里的临近空间高超声速目标,必须采用多部雷达进行组网探测。
另外,临近空间高超声速飞行器在高超声速飞行时,飞行器与大气强烈作用,在飞行器周围会形成等离子体包覆流场[10],而包覆流场会对雷达电磁波产生衰减[11-12]。文献[11]把单位距离的衰减系数公式简化为
(1)
(2)
式中, ρ为反射系数。

(3)
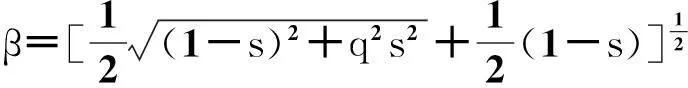
(4)
其中,s为
(5)
式中,p=fp/f为fp相对f的归一化值,q=v/2πf为等离子体碰撞频率的归一化。
总回波功率是由电磁波在空气与等离子体界面上的反射功率加上反射目标回波功率等组成的,假设等离子体参数不变,等离子体厚度为10cm,此时双程衰减为20cm,考虑fp=108~1012Hz,v/2π=107~1011Hz,C波段回波总衰减如图2所示。

(a)回波总衰减(a) Echo total attenuation
由图2可得,C波段条件下,回波总衰减最严重为22dB左右,总衰减大于5dB的范围约为总感兴趣范围的1/16(大致处于高度20~60km,速度8~15Ma的范围)。同理可得P波段条件下,回波总衰减小于8.5dB,总衰减大于2dB的范围约为总感兴趣范围的1/8(大致处于高度20~55km,速度7.6~10.3Ma的范围)。
由于等离子体对电磁波的衰减,使得雷达探测临近空间高超声速目标的难度进一步加大。所以,要通过对指定区域多部雷达装备进行优化部署,充分发挥雷达组网系统对临近空间高超声速目标的探测效能。
1.2 优化部署数学模型
地基雷达优化部署问题的数学模型为
(6)
式中,Fi(X) 为目标函数, fi(x)为约束函数,X=(x1,x2,…,xn)T为n维决策变量空间,Rm为m维解空间。不存在X使得所有子目标函数Fi(X)同时取最大值,即目标函数相互之间是冲突的。
地基雷达探测临近空间高超声速目标优化部署问题可以转化为数学上的多边形对多边形的覆盖问题,用数学语言可以描述如下:针对来袭目标的可能发射地点和攻击对象,确定目标可能经过的区域Q,其面积为S,对于不同类型雷达Ri(i=1,2,…,n,表示不同雷达程式其探测范围可能为圆形、圆环、扇形等),假设第i种程式的雷达对h高度层的覆盖范围为Sih,第j部雷达的中心记为(xij,yij)。该问题转换为求解一种优化方案,使得雷达对多边形的覆盖率α达到某一数值α0,即α≥α0,雷达探测面积重叠率β小于或等于某一数值β0,即β≤β0,同时,使用雷达的数量m(m≥m0)最小,所需雷达的最少值m0为理想值,即区域所需覆盖的面积除以单个平台覆盖面积。要使部署方案效益最大,即问题解目标为
(7)
式中,ξh为h高度层的权重,约束条件为α≥α0,β≤β0,(xj,yj)∈Q。在工程应用中,各目标之间常常难以很好兼顾,所以,采用改进的蚁群算法,通过建立多个优化目标和评价指标,力求寻找较为均衡的优化方案,实现对临近空间高超声速目标的有效探测。
2地基雷达探测临近空间高超声速目标优化部署
2.1 量化指标
地基雷达探测临近空间高超声速目标的优化部署指标主要有首次发现距离、衔接高度、探测范围重叠度、责任区覆盖系数和频率重叠系数等。
1)首次发现距离
首次发现距离Ls指雷达网能有效探测到来袭目标时,目标与保护对象之间的最远距离。表达式为
(8)
式中,Lp为雷达网在p高度层对目标的首次发现距离。由于临近空间高超声速目标飞行速度极快,为了能给拦截系统提供更充足的准备时间,要求首次发现距离越远越好,如果没有提出具体要求,Ls应能满足拦截武器在预定拦截窗口实施拦截的要求。
2)威力衔接高度
临近空间高超声速目标能够在临近空间进行跳跃飞行,为了保证雷达网在临近空间各高度层都具有较好的威力衔接,没有具体规定时,应以来袭目标飞行的最低高度来进行约束。衔接高度示意图如图3所示。
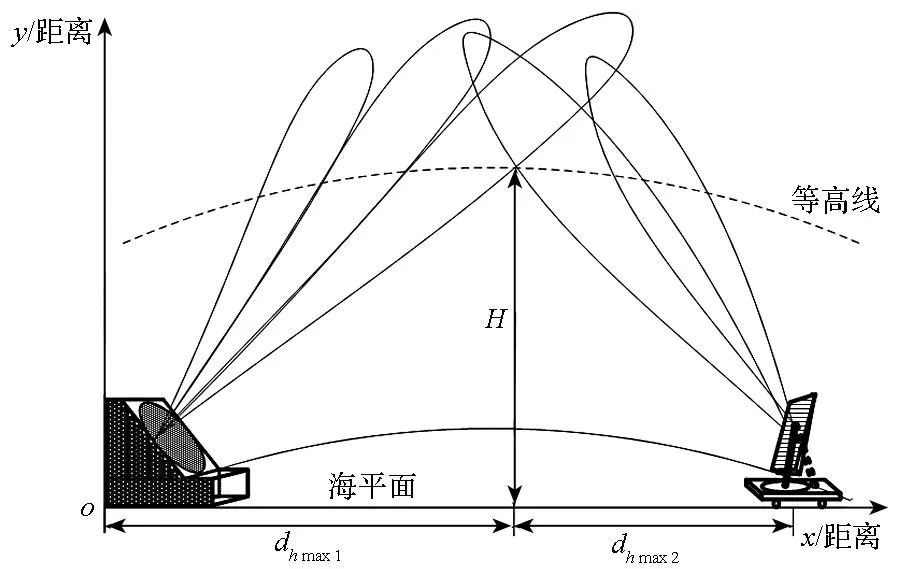
图3 衔接高度示意图Fig.3 Connect height graph
3)探测范围重叠度
相邻雷达探测范围重叠度Ch是指相邻雷达在h高度层上重叠的最大跨度与平均探测距离的比值。重叠度示意图如图4所示。
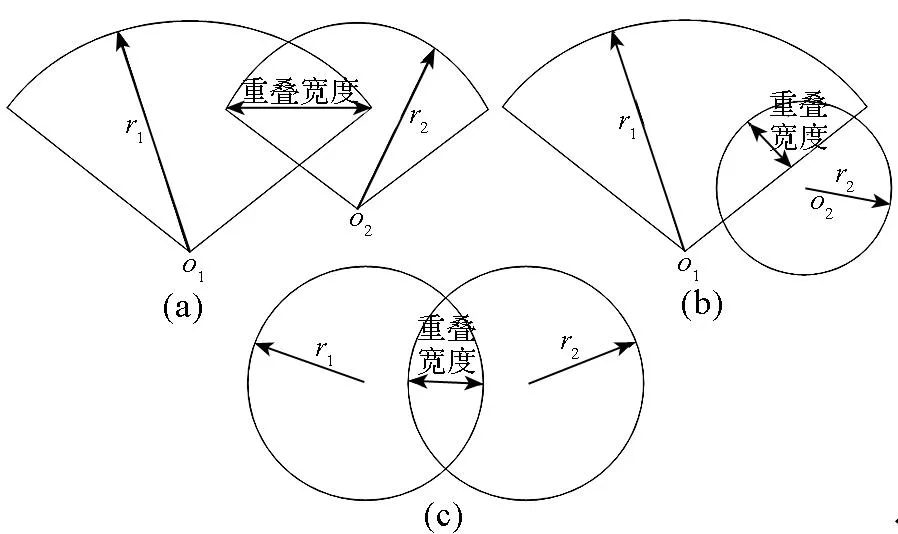
图4 重叠度示意图Fig.4 Graph degree of overlap
则相邻雷达探测范围重叠度可表示为
(9)
式中,r1、r2分别为雷达1和2的探测距离,chmax为h高度层上相邻雷达重叠的最大宽度。相邻雷达在进行任务交接时,需满足3点快速航迹起始的条件,即chmax≥3vT(v为目标速度,T为雷达探测周期)。
4)责任区覆盖系数
责任区覆盖系数ϑ是指雷达网覆盖区域与责任区域面积之比。在战场环境下,可将责任区分为警戒区域、重点区域和核心区域。为了提高雷达网对临近空间高超声速目标的连续探测能力,要求扩大警戒区域,保障重点区域,重点保护核心区域。
(10)
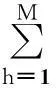
5)频率重叠系数
频率重叠系数φ是指相邻雷达的频域重叠大小和空域重叠大小的关系。为了避免同频干扰,相同频率雷达部署时要保持相对距离,并在雷达网内配置不同频率的雷达。
(11)
式中,Sih∩Sjh为第i部雷达和第j部雷达在第h高度层的探测重叠面积;fih∩fjh为第i部雷达和第j部雷达在第h高度层上频率重叠大小;Sih∪Sjh为第i部雷达和第j部雷达在第h高度层的探测面积总和;fih∪fjh为第i部雷达和第j部雷达在第h高度层上频带宽度总和。
2.2 部署模型
以上量化指标可以作为优化部署方案选取的主要依据,地基雷达探测临近空间高超声速目标优化部署的目标函数可以表示为多个高度层的优化组合函数,即
(12)
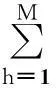
Fs=f(Ls,H,Ch,ϑ,φ,ρ)
(13)
式中,Ls、H、Ch、ϑ、φ和ρ分别为首次发现目标距离、衔接高度、探测范围重叠度、责任区覆盖系数、频率重叠系数和其他约束条件。综合考虑以上因素和雷达网部署原则,以及探测临近空间高超声速目标的特殊需求,优化部署的目标函数为
(14)
式中,ξh为各个高度层优化指数所占比重,Fsh为h高度层上雷达网连续覆盖面积。约束条件为
(15)
式中,L0、H0、C0和ρ0分别为发现目标距离、衔接高度、探测范围重叠度和其他约束条件的常数值,ϑ→1、φ→0分别表示责任区覆盖系数越大越好、频率重叠系数越小越好。另外,还有一些约束条件无法进行数学描述,如气候条件、地形条件,因此,优化部署方案最后还需要根据作战实际情况进行微调。
3基于改进蚁群算法的优化部署算法
3.1 优化部署步骤
根据作战需要、目标特性以及雷达性能等因素,对雷达网进行优化部署,采用固定部署和机动部署相结合的方式,主要分为以下几步:
1)划分防御范围
临近空间高超声速飞行器的发射点所在区域相对固定,根据其作战意图,可以预测其落点区域,如图5所示。

图5 防御区域示意图Fig.5 Defense area graph
在图5中,目标发射区域为以O点为圆心的区域,目标可以在敌国陆地、岛屿或者舰船上发射,保卫目标为P点所在的圆形区域,核心区域为来袭目标最有可能经过的区域(图中顶点为J、C、E、L),重点区域为在目标机动范围内可能攻击周边其他目标的区域(图中顶点为I、B、F、M),防御区域为由于环境、装备误差等,造成对保卫区域预测存在偏差,或者在重点区域附近存在需要保卫的目标,对重点区域进行扩大而形成的防御范围(图中顶点为O、A、G)。
2)预估雷达数目
根据作战需要、防御范围和雷达性能等,确定雷达类型及数量。结合图1和图3,确定相邻雷达威力衔接高度H以及相邻雷达在h高度层上的最大探测距离,得到相邻雷达之间的最大布站距离,并估算完全覆盖防御区域的雷达数量。
3)地基雷达部署的初始化,设置一种部署方案作为初始方案。
4)根据约束条件计算目标函数。
5)调整部署方案,对于高机动雷达,可以根据机动部署原则在优化过程中进行考虑。
6)重复步骤4和步骤5。
7)根据优化函数确定可行的部署方案,并选取最优或次优的部署方案,搜索结束。
通常在得到优化部署方案后,还需要根据实际情况进行人工微调。
3.2 改进蚁群算法
优化算法是雷达网优化部署需要考虑的一个问题,力求节省寻优步骤,快速搜索到最佳方案。改进的蚁群算法将雷达优化部署问题转换为蚁群网络,通过对初始化信息素和每次搜索结束后的信息素进行优化,提高蚁群搜索效率。改进蚁群算法流程图如图6所示。

图6 改进蚁群算法流程图Fig.6 Modified ant colony algorithm flow chart
如图6所示,初始化包括确定防御区域、核心区域范围和雷达相关参数等。搜索路径上的每个点如果满足所有约束条件,则可形成一个部署方案,当m只蚂蚁随机放在n(m≥n)个部署点上时,为了使蚂蚁快速从大量路径中找到较好的路径,k时刻待选部署点的概率P(k)为
P(k)=τ[s(k), j(k)]α·φ[s(k), j(k)]β
(16)
式中,τ、φ分别为信息素矩阵和启发因子矩阵,α、β分别为信息素重要程度参数和启发式因子重要程度参数,s(k)、j(k)分别表示k时刻已访问部署点和待访问部署点。
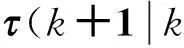
(17)
式中,ε、φ分别为信息素蒸发系数和增加强度系数,λ(k)为k时刻部署点与前一点的距离,ξ为当前部署点在防御区域中重要程度的参数。对处于核心区域的蚂蚁给出启发性的信息素,用以引导蚂蚁选择路径,剔除处于防御区域边缘的蚂蚁,因为,如果雷达中心位于防御区域边缘上,则其一半的探测范围在防御区域之外,对探测资源是一种浪费。另外,蚂蚁每次搜索结束后,对其搜索路径进行分析,比较好的部署方案则留下更多的信息素,减少下一次无效的搜索。
4仿真分析
4.1 仿真环境
假设:来袭临近空间高超声速目标距离保卫目标8000km,巡航段速度近似为匀速v≈15Ma,飞行高度h≈30km,防御区域大小为3500×6000km2,雷达程式、部署数量估算及威力(以30km高度为例)如表1所示。
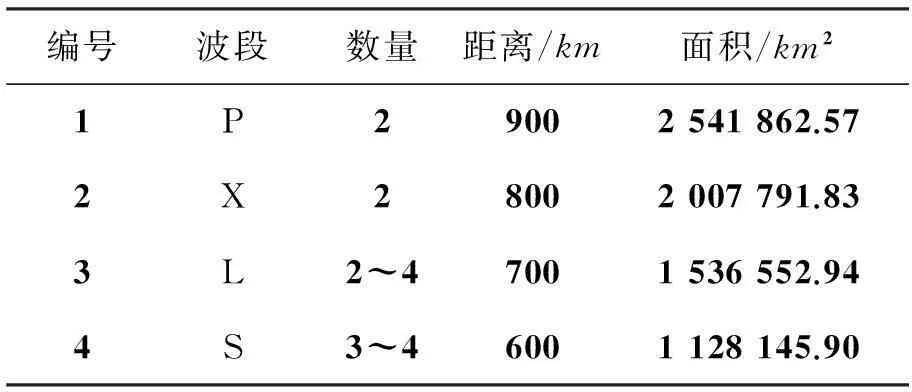
表1 雷达程式、部署数量及威力
在工程实践中,地基雷达存在顶空盲区,但本文探讨的是骨干雷达优化部署方式,其盲区可以通过相应的补盲雷达来弥补,而雷达探测临近空间目标不受地物反射干扰,气候环境相对较稳定,且防御区域远离敌方发射区域,难以实施干扰,故这里假设雷达探测区域近似为圆形。
4.2 结果分析
不同迭代次数寻优结果如图7所示(由于篇幅原因,图中横纵坐标的真实比例难以很好显示)。

(a)第20次寻优结果(a)The 20th. optimizing result
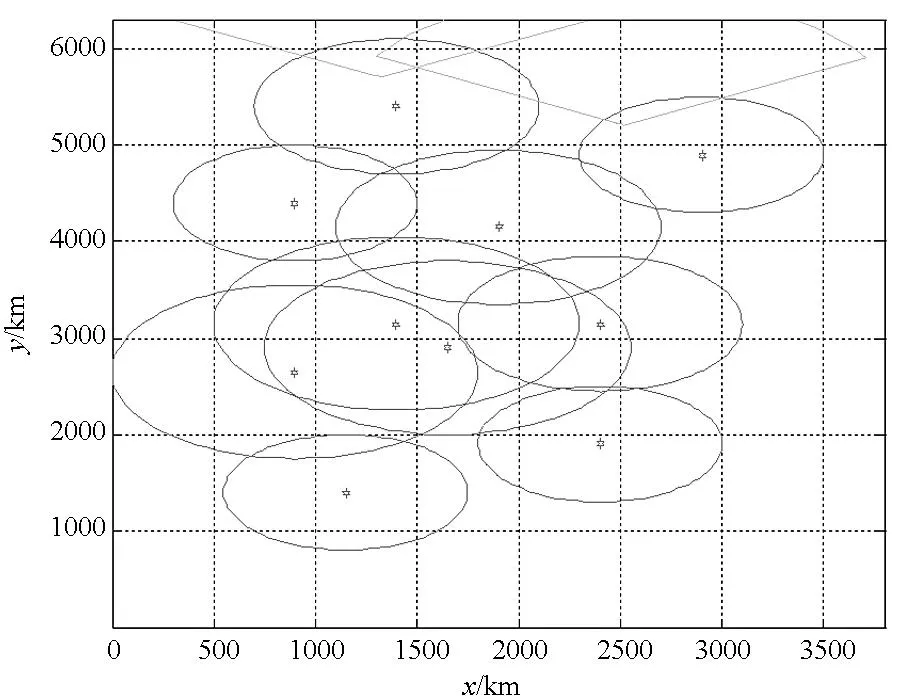
(b) 第40次寻优结果(b)The 40th. optimizing result
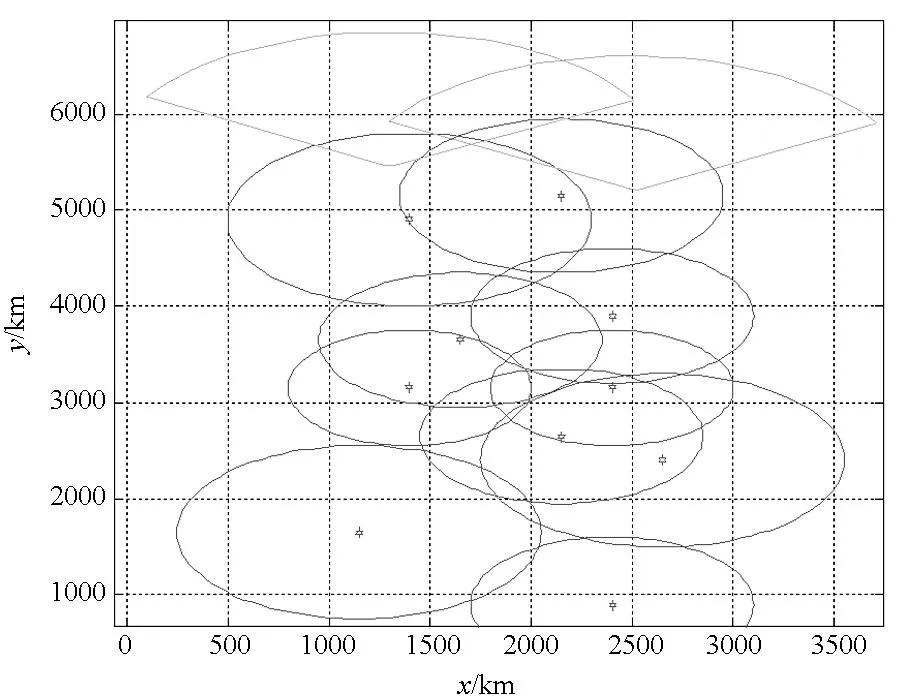
(c) 第60次寻优结果(c)The 60th. optimizing result图7 不同迭代次数仿真结果Fig.7 Simulation results of different iteration frequency
从图7可以看出,优化部署是蚁群根据约束条件,不断寻找和判断最佳部署点的过程,寻优路线及长度如图8所示。

图8 寻优路线及长度Fig.8 Optimizing path and length
图8中,左图为蚂蚁在一次寻优过程中历经的路线,右图为各次最佳寻优路线长度和寻优路线平均长度。从图中可以看出,随着迭代次数的增加,最佳寻优路线长度在不断减小,说明通过信息素的引导作用,蚁群在不断接近最优解。量化指标在计算过程中的变化情况如图9所示。

(a) 平均探测范围重叠度和首次发现距离(a) Overlap degree of average detection rangeand first find distance
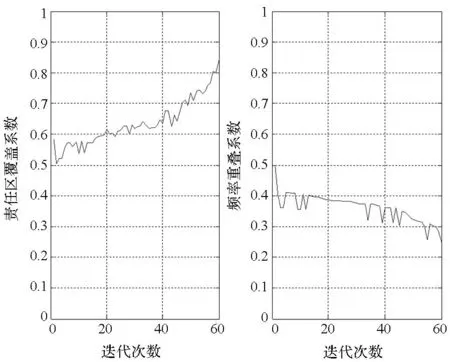
(b) 责任区覆盖系数和频率重叠系数(b) Obligation area covering factor and frequencyoverlap factor图9 量化指标变化情况Fig.9 Variation of quantize index
从仿真结果来看,随着迭代次数的增加,平均探测范围重叠度和频率重叠系数在逐渐减小,首次发现距离和责任区覆盖系数在逐渐增大。当迭代次数超过5时,责任区覆盖系数增大明显,首次发现距离和频率重叠系数接近平均值,这说明通过信息素的有效引导,大大缩小了蚁群搜索寻优的解空间,提高了优化部署的实施效率。
5结论
针对地基雷达探测临近空间高超声速目标的优化部署问题,提出地基雷达量化指标,建立优化部署模型,并改进蚁群算法中信息素的引导性。通过仿真得出以下结论:
1)新方法针对性强,能够实现多种程式地基雷达探测临近空间高超声速目标的优化部署,为地基雷达优化部署提供了一种新思路。
2)通过对信息素进行引导性的控制,能够有效提高蚁群算法的寻优速度,减少无效搜索次数。
临近空间高超声速目标与常规目标同时存在时,如何对地基雷达以及异源传感器进行优化部署,将是下一步的研究重点。
参考文献(References)
[1]Xu Y F, Jiang B, Gao Z F, et al. Fault tolerant control for near space vehicle: a survey and some new results[J]. Journal of Systems Engineering and Electronics, 2011, 22(1):88-94.
[2]Huang W, Ma L, Wang Z G, et al. A parametric study on the aerodynamic characteristics of a hypersonic wave rider vehicle[J]. Acta Astronautica, 2011, 69(3-4):135-140.
[3]曾开春,向锦武. 高超声速飞行器飞行动力学特性不确定分析[J]. 航空学报, 2013, 34(4): 798-808.
ZENG Kaichun, XIANG Jinwu. Uncertainly analysis of flight dynamic characteristics for hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(4):798-808. (in Chinese)
[4]肖松,谭贤四,王红,等. 临近空间高超声速目标断续点迹航迹起始方法[J].华中科技大学学报(自然科学版), 2014, 42(3):52-57.
XIAO Song, TAN Xiansi, WANG Hong, et al. Feasible track initiation method for near space hypersonic target[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014, 42(3):52-57. (in Chinese)
[5]马梁,王雪松,李永祯,等. 雷达部署对进动目标微多普勒频率的可测性分析[J].国防科技大学学报, 2011, 33(2):54-59.
MA Liang, WANG Xuesong, LI Yongzhen, et al. Influence of radar location on the measurability of micro-doppler detecting for precession target[J]. Journal of National University of Defense Technology, 2011, 33(2):54-59. (in Chinese)
[6]张远,方青,曲成华.基于遗传算法的组网雷达优化部署[J].雷达科学与技术, 2014, 12(1):76-80.
ZHANG Yuan, FANG Qing, QU Chenghua. Optimal deployment of netting radars based on genetic algorithms[J]. Radar Science and Technology, 2014, 12(1):76-80. (in Chinese)
[7]Gao S. Optimal deployment problems of radar network[J]. Research Journal of Applied Sciences, Engineering and Technology, 2013, 6(10): 1879-1883.
[8]刘彦君,黄金才,王江. 有源干扰条件下基于NSGA-Ⅱ的雷达网优化部署方法[J]. 指挥控制与仿真, 2014, 36(1):36-40.
LIU Yanjun, HUANG Jincai, WANG Jiang. Optimal deployment of radar network based on NSGA-Ⅱ under active jamming[J]. Command Control & Simulation, 2014, 36(1):36-40. (in Chinese)
[9]Cui Y J, Cha H, Tian B. Cultural shuffled frog leaping algorithm and its applications for the radar network deployment[J]. Applied Mechanics and Materials, 2014, 624:516-519.
[10]乐嘉陵. 再入物理[M]. 北京:国防工业出版社, 2005.
YUE Jialing. Re-entry physical[M].Beijing:National Defense Industry Press, 2005. (in Chinese)
[11]Garg P, Dodiyal A K. Reducing RF blackout during re-entry of the reusable launch vehicle[C]//Aerospace Conference, IEEE, 2009:1-15.
[12]Pippert G F. On the structure of wake turbulence deduced from field radar measurements[C]//AIAA Conference on Physics of Entry into Planetary Atmosphere, 1963:6320446.
Deployment optimization method for ground-based radar to detect near space hypersonic target
XIAOSong,TANXiansi,WANGHong,WANGYi
(Air Force Early Warning Academy, Wuhan 430019, China)
Abstract:In order to improve detection ability of ground-based radar to near space hypersonic target and explore a practical and efficient deployment optimization method, the difficulties and mathematical models of the ground-based radar to detect near space hypersonic target were analyzed and the deployment principle and quantitative indicators of it were put forward. Deployment optimization model of ground-based radar was established and the ant colony algorithm controlled by introductory pheromone was designed. The simulation results show that this method can achieve a variety of programs of ground-based radar deployment optimization, improve the efficiency and operability of the ground-based radar deployment optimization, and provide a new way of thinking for ground-based radar to detect near space hypersonic target.
Key words:deployment optimization; ground-based radar; near space; hypersonic; ant colony algorithm; detection
中图分类号:TN95
文献标志码:A
文章编号:1001-2486(2015)02-121-07
收稿日期:2014-08-11基金项目:国家自然科学基金资助项目(61271451)
作者简介:肖松(1985—),男,湖北武汉人,博士研究生,E-mail:tracyoioi@163.com;谭贤四(通信作者),男,教授,博士,博士生导师, E-mail: tanxs-hust@163.com
doi:10.11887/j.cn.201502023
http://journal.nudt.edu.cn
