一种新的多维IRT模型——高阶IRT模型
2015-02-25潘浩
潘 浩
(辽宁医学院国际教育学院,辽宁 121000)
一种新的多维IRT模型——高阶IRT模型
潘浩
(辽宁医学院国际教育学院,辽宁 121000)
摘要:早期的单维IRT模型忽视了测验多维性的可能,而多维IRT模型对各维度的划分不够明确,不能良好反应各维度能力的内涵。高阶IRT模型承认测验的多维性,以分测验划分维度,同时又将多个维度的能力统一到一个高阶的能力中,能够在了解被试各维度能力的同时,为被试提供整体的能力估计,它能更好地反映实际,并且适应大规模测验的需求。
关键词:高阶IRT;多维IRT;单维IRT
1引言
项目反应理论(IRT)是关于被试潜在特质(能力水平)与其对测验项目反应之间关系的理论(王孝玲,2005)。它能够反映单一被试和单个项目间的关系,提供更精确的测量指标,解决了CTT样本和测验的相互依赖的问题。项目反应理论(IRT)发展至今,依据基本假设的不同主要有单维IRT模型和多维IRT模型两种。
2常见的IRT模型
2.1单维IRT
单维性假设是指每个测验只考察一种能力,或者可解释为影响测验表现的只有一种“主导”因素。
第一个IRT模型是Lord在他1952年(Lord,1952)的博士论文中提出的双参正态拱形模型,以正态累积分布的函数形式作为项目的反应函数。其数学表达形式如下:
丹麦学者Rasch(Rasch,1960)提出了Rasch模型,这是最简单的单维IRT模型。其数学表达式如下(转引自Embretson&Reise,2000):
Birnbaum(1968)在Rasch单参逻辑斯蒂模型的基础上,又发展出双参,三参逻辑斯蒂模型。表达式如下:
其中a是项目的区分度,c是曲线的下渐近线位置,代表猜测度。当c值越大,下渐近线越高,猜测度越大。
单维IRT模型简单明了,实现了对被试能力和题目质量的同时估计,但是在实际测验中,常常需要几种能力共同或者有所侧重地完成测验任务,利用单维IRT模型显然不能提供全面的信息。
2.2多维IRT
为了解决单维IRT的局限,Robert和Mark(1982)对多维IRT进行了研究。多维项目反应理论模型是以多维度心理机制为前提,通过引入各维度上的能力和项目参数,来表征被试与项目之间交互作用的一种非线性数学模型。在心理和语言测验中,许多测验的完成实际上需要不止一种能力,多维IRT模型的出现在理论假设上较好地符合了实际(Reckase,1997)。
目前较常见的是补偿性和非补偿性两种模型。所谓补偿,就是在被试完成或作答某一项目时,由多种能力共同产生作用影响被试的反应情况,当所需要的一种能力偏低时,所需要的其他能力的高水平可以弥补。而非补偿性是假设一个问题的解决或者一个项目的完成是由多个能力共同决定的,它们之间是不能相互补偿的,正确反应概率的上限取决于能力结构中最低的那一项(Reckase,1997)。
三参多维补偿性模型
Xij是指被试i在项目j上的得分,θik表示被试i在第k个维度的能力参数向量,αjk是第j个项目在第k个维度的区分度参数向量,bj是第j个项目的难度系数等级。需要说明的是,每个项目每一个维度都有一个区分度参数,但每个项目只有一个项目难度参数,不依维度不同而变化。
三参多维非补偿性模型(Sympson,1978)
其中,m是维度,a,b,c是项目的区分度,难度和猜测度参数。
补偿性模型每个项目有一个难度系数和一个猜测度,在每个维度上有一个区分度参数,完成项目的能力是多个维度能力的和。而非补偿性模型每个项目在每个维度上都有一个区分度参数和一个难度系数,这个模型也可以写成多个单维双参逻辑斯蒂模型的积。
多维IRT解决了单维性假设与测验实际不符的问题,但是完成一个测验或者一张试卷通常需要几种不同的能力,虽然这些能力可能不是完全按照分测验严格区分,但是往往有所侧重。在实际的参数估计中,根据不同维度的能力参数估计值来判断项目所属的分维度,因此常常有分维度包含的项目过少的情况,不足以确保参数估计的精确性。另外,参与测验的被试往往需要一个整体的评价,即对整体能力的一个估计,而传统的单维IRT虽然可以完成整体能力的估计,但完成测验所需能力的多维性假设显然是与单维IRT不符的。因此,无论是传统单维IRT还是多维IRT,都在参数估计上存在一定问题而偏离实际需求。
在这种背景下,Song(2007)在Ahigher-orderitemresponsemodel:Developmentandapplication一书中首次提出了一种高阶IRT模型。高阶IRT模型是以能力的不同层次为前提假设的,即影响被试测验表现的是两个层次的能力,处于高层的是一个整体的高阶能力,而这个高阶能力又是由一组低层次的不同分能力组成的。
3高阶IRT模型内涵
高阶IRT假设测验是一个维度内单维的多维测验,它依照分测验来划分能力维度,每一个分测验测量一个并且只测量一种能力,因此,它所假设的能力结构实际上是一种比较简单的多维测验的能力结构,只是在多种能力之上多了一个高层次的整体能力。

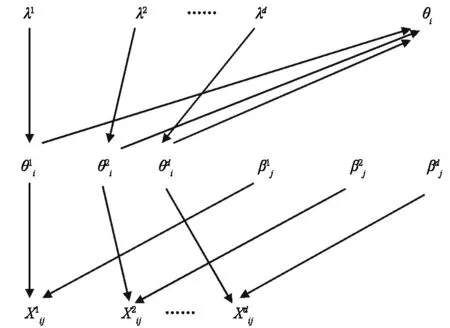
图1 高阶IRT层次结构图
高阶IRT模型所选取的数学形式是三参逻辑斯蒂模型。它的数学表达如下:
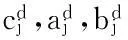
如果用整体能力和相关系数来表示维度能力,简化一下项目参数的表示方法,则变为:
4高阶IRT的研究进展
最初的研究者通过模拟实验,研究了高阶IRT模型和其他IRT模型在参数估计方面的表现。Song(2007)提出了高阶IRT模型,书中详细阐述了从经典测验理论到IRT的发展历程,并利用高阶IRT模型进行了模拟实验。HaoSong使用了贝叶斯等级框架下的MCMC方法,分别采用传统单维IRT和高阶IRT对模拟数据进行了参数估计。HaoSong通过变化不同测验长度,不同维度数,分测验间不同的相关系数进行了对比实验。结果显示,当分测验间相关极低或者不相关时,高阶IRT的估计效果明显好于传统单维IRT,而当分测验间相关较高时,两者估计结果差不多,但高阶IRT更为准确。
delaTorre和Song(2009)采用同样方法对高阶IRT模型与传统IRT模型进行了对比研究。此外,他们又利用了CTB/McGraw-Hill九年级测验的实测数据对两个模型的能力参数估计情况进行了对比分析。结果显示,两个模型在分测验间相关高时在整体能力估计上差异不大,高阶IRT的标准差和测验偏差(bias)更小。当分测验间相关较低时,高阶IRT的估计效果明显更好。Jimmy和YuanHong(2010)利用了同样的方法针对小样本数据进行了模拟和实测数据的估计,结果显示,当样本数量小且维度数较多时,高阶IRT体现出了明显优势,标准误和测验偏差明显更小,证明高阶IRT利用测验内维度间相关信息这一点是对参数估计的一次改进(Hung,Wang,Chen,&Su,2013;Huang&Wang,2013)。
后来的研究者主要利用自编测验,对高阶IRT进行实践检验,并对比几种IRT模型的估计效果。Yang等(Yang,Kuo,&Liao,2011)设计了一个分数乘法的计算机自适应性测验,并利用高阶IRT模型对被试的整体能力和分能力进行了估计,并利用整体能力估计结果对被试进行了整体的评价,利用分能力估计结果对存在的学习障碍进行诊断。Chih-WeiYang等将数学能力分成概念性知识、程序性知识和解决问题的能力三种分能力。结果显示,计算机对于学习障碍的诊断和人工评分对于学习障碍的诊断平均一致性高达97%,而利用高阶IRT模型估计出的分能力和在该能力维度内学习障碍的数量之间呈现高相关,结果证明学习障碍越多,被试的数学能力越差。台湾学者孙长荪(2010),张胜凯(2009),黄子晏(2010),苏启明(2010),张素珍等(2010)通过对自编测验的分析,比较单维、多维和高阶IRT模型,结果表明高阶IRT能提供更多信息,效果更好。
上述研究结果显示,高阶IRT模型较之传统单维IRT模型和多维IRT模型的估计结果更为精确(误差小),且能够同时估计整体能力和分能力,提供较多信息。但是针对实测数据的研究还很少,在实际应用上说服力不强。国外学者采用模拟实验预先设定了项目参数,这对能力的估计会产生一定影响,台湾学者自编的测验项目过少(有的分测验甚至只有三道题),题目质量对估计结果的影响很大。
5小结和展望
高阶IRT模型利用了分维度能力和整体能力的相关,实现了对两个层次能力的同时估计,是对IRT的进一步发展,也是在能力结构假设上的一次新的突破。高阶IRT模型能够提供被试分项和整体能力的估计,是符合大规模测验的实际需求,对心理和教育测量有着实践意义的。
高阶IRT在整分能力关系上采用了线性相关,这是一种简单的相关关系,然而相关关系还可能更加复杂,比如非线性相关。因此,所选取的相关关系是否需要调整还有待进一步证实。另外,高阶IRT模型的一个重要假设是维度内单维,即项目间或分测验间单维,而在实际测量中,项目内或者分测验内是否存在多维情况,将分测验划为单维测验是否过于笼统有待进一步研究。
参考文献
黄子晏.(2010).阶层式试题反应理论之多点计分模探讨.2013-10-15取自http://ndltd.ncl.edu.tw/cgi-bin/gs32/gswev.cgi
苏启明.(2010).高阶层试题反应理论模式延伸与应用.2013-10-15取自http://ndltd.ncl.edu.tw/cgi-bin/gs32/gsweb.cgi
孙长荪.(2010).以NAEP数学评量中数学能力架构进行国小六年级几何测验的编制与分析.研究所硕士论文.国立台中教育大学教育测验统计.
王孝玲.(2005).教育测量(修订版)(p.242).上海:华东师大出版社.
张素珍,李佩瑾,郭伯臣,林佳桦.(2010).应用HIRT于实证资料分析—以国小六年级数学小数的除法单元为例.测验统计年刊(台湾),第十八辑,51-66.
张胜凯.(2010).使用HIRT模式建立国小六年级学童数学推理能力测验.硕士论文.国立台中教育大学教育测验统计研究所.
Birnbaum,A.(1968).Some latent trait models and their use in inferring an examinee’s ability.In F.M.Lord & M.R.Novick(Eds.),Statisticaltheoriesofmentaltestscores(pp.17-20).Reading,MA:Addison-Wesley.
de la Torre,J.,& Song,H.(2009).Simultaneous estimation of overall and domain abilities:A higher-order IRT Model Approach.AppliedPsychologicalMeasurement,33(8),620-639.
de la Torre,J.,& Hong,Y.(2010).Parameter estimation with small sample size a higher-order IRT Model Approach.AppliedPsychologicalMeasurement,34(4),267-285.
Huang,H.Y.,Wang,W.C.,Chen,P.H.,& Su,C.M.(2013).Higher-Order Item Response Models for Hierarchical Latent Traits.AppliedPsychologicalMeasurement,37(8),619-637.
Huang,H.Y.,& Wang,W.C.(2013).Higher order testlet response models for hierarchical latent traits and testlet-based items.EducationalandPsychologicalMeasurement,73(3),491-511.
Lord,F.M.(1952).A theory of test scores.PsychometricMonographs,(7),84.
Rasch,G.(1960).Probabilitymodelsforsomeintelligenceandattainmenttests.Copenhagen:Paedogogiske Institute.
Reckase,M.D.(1997).The past and future of multidimensional item response theory.AppliedPsychologicalMeasurement,21(1),25-36.
Song,H.(2007).A higher-order item response model:Development and application.Unpublished doctoral dissertation.TheStateUniversityofNewJersey,95-107.
Sympson,J.B.(1978).A model for testing with multidimensional items.In D.J.Weiss(Ed.),Proceedingsofthe1977ComputerizedAdaptiveTestingConference.Minneapolis:University of Minnesota.
Yang,C.W.,Kuo,B.C.,& Liao,C.H.(2011).A HO-IRT based diagnostic assessment system with constructed response items.TheTurkishOnlineJournalofEducationalTechnology,10(4),46-51.
A New Multidimensional IRT——Higher-Order IRT Model
Pan Hao
(International Education College,Liaoning Medical University,Liaoning 121000)
Abstract:Item Response Theory(IRT)is a well known theory which can reflect the relationship between latent trait and items.However,both unidimensional IR model and multidimentional IRT model are short at reflecting ability structure precisely and appropriately.The Higher-Order IRT(H-O IRT)model is a multi-unidimensional model that uses in-test collateral information and represents it in the correlational structure of the domains through a higher-order latent trait formulation.H-O IRT model can provide both domain and the whole information,which is better fulfilling the needs of large-scale tests.
Key words:H-O IRT;Multidimensional IRT;Unidimensional IRT
中图分类号:B841.2
文献标识码:A
文章编号:1003-5184(2015)05-0448-04
