探索性因子分析中主轴法下的平行分析



探索性因子分析中主轴法下的平行分析

高石1，杨莉萍1*，白福宝2

(1.南京师范大学心理学院，南京 210097；2.安徽农业大学人文社会科学学院，合肥 230036)

摘要：在探索性因子分析中，决定因子的提取数至关重要。平行分析是确定因子提取数较为常用的方法。目前国内的心理学研究较多使用主成分方法下的平行分析，对主轴方法下的平行分析则鲜有论及。本研究介绍了主轴方法下平行分析的原理，并以具体实例说明了该方法在心理统计中的具体运用，希望藉此解决以传统方法确定因子提取数所存在的问题。

关键词：探索性因子分析；主轴法；平行分析

1以传统方法确定因子提取数存在的问题

因子分析是目前使用最为广泛的多元统计分析方法。它是用少数几个因子来描述许多指标或变量间的联系，在某一事物所蕴含的众多变量中寻找能够描述该事物的几个潜变量(或因子)的统计方法。该方法最早于1904由英国心理学家斯皮尔曼在研究智力结构时提出。其发表的论文《客观决定和测量一般智力》(General Intelligence，Objectively Determined and Measured)被视为因子分析方法诞生的标志。然而，在使用因子分析方法的过程中，确定因子提取的个数一直是个比较棘手但又至关重要的问题。有研究者认为，它可能比因子提取和因子旋转方式的选择更为重要。

目前确定因子提取个数最为常用的方法是特征值大于1准则和Cattell陡阶检验(又称碎石图检验)。这两种方法之所以常用，可能在于它们是SPSS的默认选项。然而这些方法自身存在一定的局限性。对于特征值大于1准则而言，Hayton(2004)提出存在三种批评：首先，运用特征值大于1准则将得到总体相关矩阵的秩(the rank of population correlation matrix)的下限(Guttman，1954)。相关矩阵的秩等同于最小抽取的因子个数。因此，在实际操作中，我们将其视为抽取因子数的标准并不合理。其次，这一准则适用于总体相关矩阵，而在实际操作中，由于抽取的是样本，抽样误差往往会增加矩阵的秩，导致所抽取的因子数过多(Horn，1965)。第三，研究者有时会面临特征值略高或略低于1的情况。在使用这一规则时，常常表现得武断(Fabrigar et al.，1999)。当前在SPSS中，无论使用哪一种因子提取方法，都使用特征值大于1的准则。而有研究者指出，这一准则只适用于主成分分析，在主轴法中是不适用的(Russell，2002)。对于Cattell陡阶检验，因其主观性和武断性，所遭受的批评更多。例如，在特征值之间不存在明显突变(break)时，很难确定适当的因子提取数。

2基于主轴因子法的平行分析原理

在众多确定因子提取数的方法之中，平行分析(Parallel Analysis)是较为理想的方法之一。该方法是由Horn(1965)提出的平行检验方法发展而来。平行分析基于对矩阵特征值的计算与比较，通过比较真实数据矩阵与随机数据矩阵特征值的平均值或第95百分位数来决定因子的取舍(Russell，2002)。比较均值或是第95百分位数的结果通常具有一致性。假如出现不一致，则比较第95百分位数可以避免选取因子数过多(Hayton，2004)。因此，平行分析的关键在于矩阵特征值的计算。

目前探索性因子分析主要采用两种方法：主成分分析法和主轴因子法。在使用这两种方法时，特征值计算所依据的矩阵有所不同，分别为相关矩阵和约相关矩阵。相关矩阵通常表示为R，约相关矩阵通常表示为R*(方便起见，以下直接使用R和R*表示)，由此产生相对应的两组特征值，即R的特征值和R*的特征值(颜铁成，2007)。这里R与R*的区别在于矩阵对角线元素。前者对角线元素均为1，后者的对角线元素则可采用多种方法进行估计，例如最大相关法(max|r|)，参照析因迭代法(iteration by refactoring)，复相关系数的平方(squared multiple correlation，简称SMC)等(王权，1993)。此外，Widaman(1985)提出，可用复相关系数的平方作为初始估计，通过不断迭代，使用最小二乘法来估计矩阵的对角线元素。

主成分分析是依据R的特征值进行，其假定所有观测变量的方差都能为公因子所解释，即公因子方差为1。而主轴因子法则是基于R*的特征值进行的，其假定所有观测变量的方差不一定完全被公因子所解释，公因子方差不一定是1。基本预设不同原本是主成分分析与主轴因子法之间的一个重要区别(孙晓军，周宗奎，2009)。但在实际运用中，无论是采用主成分分析还是主轴因子法，SPSS所给出的特征值都是基于主成分分析法所得到的特征值(颜铁成，2007)。有研究者比较这两组特征值的大小，发现R矩阵的特征值通常要比R*的特征值要大(颜铁成，2007)。因此，在采用主轴因子方法的前提下，根据SPSS所输出的特征值来进行平行分析是不合理的。

主轴法下平行分析的做法应该是：首先对约相关矩阵R*的主对角线元素进行估计，产生真实数据的约相关矩阵R*的估计矩阵，以此计算出对应的特征值。再按照相同过程计算出随机矩阵的约相关矩阵R*的特征值。随机矩阵的被试人数和变量数要求与真实矩阵相同。因为特征值代表了因子所解释的变异，通过比较真实数据的特征值与随机数据的特征值可以决定因子的取舍。当从真实数据中抽取的因子所解释的变异比从模拟的随机数据中抽取的相应因子所解释的变异大时，应保留该因子，否则当舍弃。

以下拟借助一个实例，说明在主轴因子法下应如何正确使用平行分析。

3基于主轴因子法的平行分析实例

3.1工具性软件

实现平行分析的具体方法有很多，例如在SPSS、SAS中通过编写程序语言来实现(Oconnor，2000)，或使用具有平行分析功能的软件Vista(The Visual Statistics System)(Young，2003)等。前者所涉及的软件虽具有较高的普及性，但编写程序语言并非易事。尽管已经有研究者公布了这一实现过程的程序语言，然而对于一般的初学者，仍然很不方便。因此，本研究选择采用第二种方法。Vista是由北卡罗来纳州大学教堂山分校教授Young及其学生历时10年开发的一种可视化统计分析软件。该软件是公开、免费的，可以直接从开发者的网站下载。软件的安装、运行、导入数据、分析数据等一系列操作均在可视化操作界面上完成，易于掌握。

3.2数据来源

本案所使用的数据来自一项对大学生公正感的问卷调查研究。该研究在文献研究的基础上，通过规范的量表编制程序，编制了与大学生公正感有关的特质公正感问卷，来了解大学生公正感的基本情况。该问卷采用自陈方式，共包含24个题项，从“1-非常不符合”到“5-非常符合”，共分五个等级计分。

本案采用分层随机抽样，在福建、浙江和江苏3省的六所大学抽取大学生被试，共发放问卷430份，回收有效问卷409份，回收有效率为95.12%。信度检验表明为，问卷测量的内部一致性系数为0.882，达到显著水平。

3.3统计处理

首先，使用SPSS16.0对数据进行分析，数据的KMO测量值为0.860，处于0.80.9之间，表明适合作因子分析。本研究的主要目的在于提供如何在主轴法下进行平行分析的样本，因而选用主轴法来提取因子和计算特征值。表1是使用Vista对数据进行平行分析得出的结果，同时根据表1结果绘制了图1：

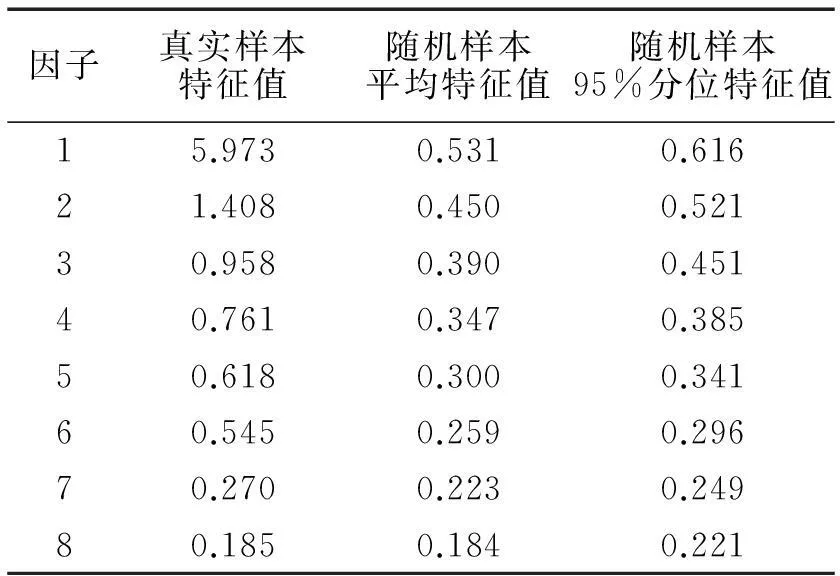
表1　真实样本与随机样本的特征值比较

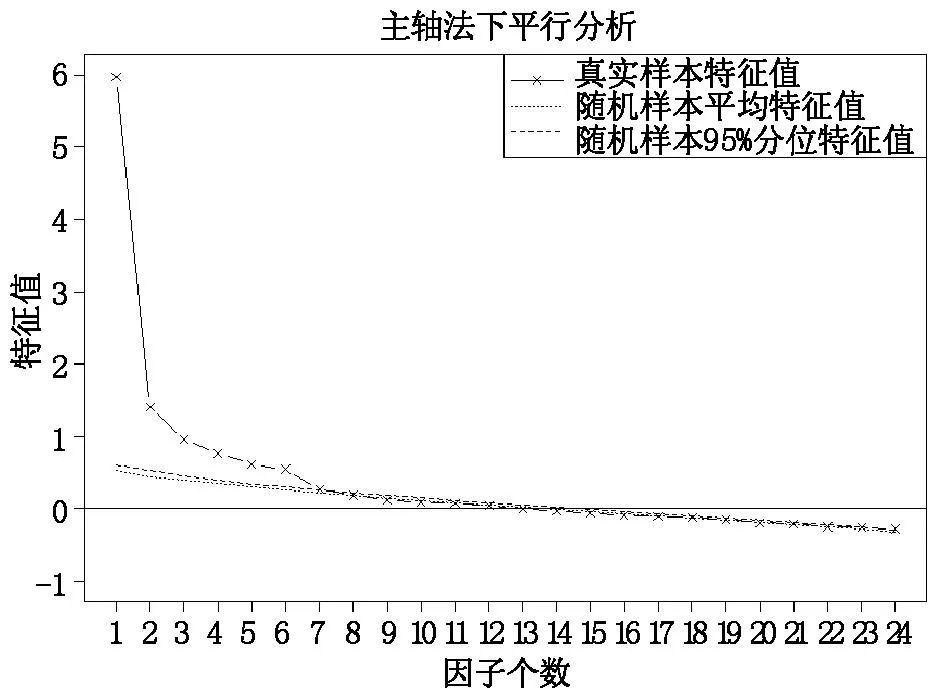
图1　真实数据特征值与随机数据特征值比较

从表1可以看出，真实数据特征值在第八个因子时大于随机数据特征值的平均值，但小于95%分位值。根据前文提到的原则，比较随机数据特征值第95百分位数，保留七个因子。同时应参考这七个因子对方差的累积贡献率以及经旋转后因子的可解释性。如果这七个因子的方差贡献率太低，则可考虑适当多保留一些因子。图1显示，因子数在13以后出现了负值。这是因为当R的对角线元素被小于单位1的数取代后，比如，用变量的公共因素的估计值取代后，从理论上说，矩阵的R的正定和半正定特性将得以保持。但在实际操作中，约相关矩阵R*并没有保持正定和半正定性，此即会有负的特征值出现(王权，1993)。

在此需要说明的是，由于对R*的对角线元素进行估计有多种方法，因此采用不同的估计方法所算出的特征值会略有不同，但并不会对平行分析的结果产生实质性影响。本研究所使用的Vista在对R*对角线元素进行估计时，采用的是前文提到的复相关系数的平方作为估计值，进而计算出特征值。这一方法与前文提到的SPSS程序语言所使用的方法一致(Oconnor，2000)。另外，对于因子个数的保留问题还应参照其他标准，进行综合判断，即在遵守简约性原则与完备性原则的前提下，根据研究者前期的理论建构、自身的专业知识及研究经验综合决定因子的取舍(沐守宽，顾海根，2011)。

致谢：感谢美国西北大学William.Revelle教授，爱荷华州立大学Daniel W.Russell教授以及南京师范大学数学系周宇给予本研究的指导和帮助。

参考文献

沐守宽，顾海根.(2011).探索性因素分析因子抽取方法的比较.心理学探新，31(5)，477-484.

孙晓军，周宗奎.(2005).探索性因素分子分析及其在应用中存在的主要问题.心理科学，28(6)，1440-1442.

王权.(1993).现代因素分析.杭州：杭州大学出版社.

颜铁成.(2007).因素分析中三种特征值大小的比较.统计与决策，4，134.

Fabrigar，L.R.，Wegener，D.T.，MacCallum，R.C.，& Strahan，E.J.(1999).Evaluating the use of exploratory factor analysis in psychological research.PsychologicalMethods，4，272-299.

Guttman，L.(1954).Some necessary conditions for common factor analysis.Psychometrika，19，149-162.

Hayton，J.C.(2004).Factor retention decisions in exploratory factor analysis：A tutorial on parallel analysis.OrganizationalResearchMethods，7(2)，191-205.

Horn，J.L.(1965).A rationale and test for the number of factors in factor analysis.Psychometrika，32，179-185.

Oconnor，B.P.(2000).SPSS and SAS programs for determing the number of components using parallel analysis and Velicer’s MAP test.BehaviorResearchMethods，32(3)，396-402.

Russell，D.W.(2002).In search of underlying dimensions：The use(and abuse)of factor analysis in personality and social psychology bulletin.PersonalityandSocialPsychologyBulletin，28(12)，1629-1646.

Widaman，K.F.，& Herringer，L.G.(1985).Iterative least squares estimates of communality：Initial estimate need not affect stabilized value.Psychometrika，50，469-477.

Young，F.W.(2003).Vista(The Visual Statistics System).[computer software] [on-line].Retrieved from http：//forrest.psych.unc.edu/research/index.html.

The Application of Parallel Analysis Based on(Using)the Principal

Axis Factoring in Exploratory Factor Analysis

Gao Shi1，Yang Liping1，Bai Fubao2

(1.School of Psychology，Nanjing Normal University，Nanjing 210097；

2.School of Humanities & Social Sciences，Anhui Agricultural University，Hefei 230036)

Abstract：The decision of how many factors to retain is a critical issue in exploratory factor analysis.Parallel analysis(PA)is one of the most commonly used methods.Present domestic studies have focused mainly on parallel analysis using principal component factoring(PA-PCF)，but parallel analysis using principal axis factoring(PA-PAF)is rarely found.In this article，the rationale of PA-PAF is introduced and the specific procedure of conducting PA-PAF in exploratory factor analysis by using raw data is presented in order to deal with the challenge of factor retention encountered in traditional methods.

Key words：exploratory factor analysis；principal axis factoring；parallel analysis

中图分类号：B841.2

文献标识码：A

文章编号：1003-5184(2015)05-0471-03

通讯作者：*杨莉萍，E-mail：lpy2908@yahoo.com.cn。