Modelling As-Cast Structure and Macrosegregationin Ingot Casting

Wu M, Kharicha A, Ludwig A

(1． Christian-Doppler Laboratory for Advanced Process Simulation of Solidification & Melting,

University of Leoben, A-8700 Leoben, Austria)

(2．Department of Metallurgy, University of Leoben, A-8700 Leoben, Austria)



Modelling As-Cast Structure and Macrosegregationin Ingot Casting

Wu M1,2, Kharicha A1,2, Ludwig A2

(1． Christian-Doppler Laboratory for Advanced Process Simulation of Solidification & Melting,

University of Leoben, A-8700 Leoben, Austria)

(2．Department of Metallurgy, University of Leoben, A-8700 Leoben, Austria)

Abstract：Since 1960s the formation mechanisms of the as-cast structure and macrosegregation during solidification of steel ingots were systematically studied by Flemings and other researchers, and understanding to this issue was significantly achieved, but there is still no mathematical model which can quantitatively predict them. Reason is due to the complexity of the involved multiphase flow phenomena, e.g. interdendritic flow in the mush, sedimentation of free moving (equiaxed) crystals, etc.All these multiphase flow phenomena are coupled with the solidification thermodynamics and diffusion kinetics, affecting the formation of as-cast structure. The development of multiphase computational fluid mechanics (MCFD) and its application in the study of solidification in last two decades provide a new tool for solving the above problem. This article is going to give a brief review of the progress in this area. Some examples are presented to demonstrate the potential and limitations of this tool for the calculation of the as-cast structure and macrosegregation in ingot castings.

Key words：solidification；ingot；macrosegregation；as-cast structure；numerical modeling CLC number：TG111.4Document code： AArticle ID：1674-3962(2015)09-0640-12

铸锭宏观组织和偏析的数值仿真

1Introduction

Most valuable experimental researches on the as-cast structure and macrosegregation in steel ingots were performed approximately one century ago[1-2]. A series of steel ingots, scaled from a few hundred kilograms up to 172 tons, were poured and sectioned for segregation and structure analyses. Today due to extremely high costs these kinds of experiments are only carried out occasionally and with caution[3-6].Instead, the mathematical (both analytical and numerical) modelling becomes the most efficient tool for this study. Systematic study of the formation mechanisms of macrosegregation by using mathematical model can trace back to 1960s[7]. By now, fundamentals of the macrosegregation are mostly understood[8]: “all types of macrosegregation form within the liquid-solid zone, not in front of it. In most cases, it is the results of slow interdendritic flow, driven by shrinkage, geometry, solid deformation or gravity. In some cases it may be the results of solid movement in the early stage of solidification (i.e.settling).”More about the state-of-the-art knowledge on this topic can be read in some recent review articles[6, 8-11].

Mostly-occurring phenomena during solidification, which concern the formation of as-cast structure and macrosegregation in an ingot casting, are illustrated in Fig.1. Firstly, it is multiphasic by nature. The involved phases interact with each other, and multiphase flow is not avoidable. Secondly, the solidifying phases appear with different crystal morphologies (stationary columnar, moving equiaxed), which affect the interphase interactions, hence to a large extend influence the flow. Thirdly, solidification thermodynamics and diffusion kinetics which occur at the microstructure scale are also fully coupled with the aforementioned multiphase flow. It means that an ideal model for macrosegregation should consider multiphase flow, different crystal morphologies, and span a wide range of length scales. In the last few decades great progresses have been made, and more and more powerful solidification models have been developed at both the macro- and microscopic scales[12-15], but a model covering all fields of physics and spanning all length scales is far from completion.It is still quite challenging to predict macrosegregation in an ingot casting quantitatively.

Fig.1　Schematic illustration of the multiphase phenomena during solidification of a metal casting

The volume average based Eulerian approach is considered to be the most promising method to describe the above issue at the process scale. The reasons lie on the power and flexibility of this approach in dealing with the multiple transport phenomena. All the transport phenomena occurring during solidification, as far as they are able to be properly described with the transport equations, can be included in one model. The number of phases is theoretically limited by the computational capability. A bridge of the physical phenomena occurring at different length scales can be made by the proper description of the corresponding exchange and source terms, which are implemented in the global transport equations by closure laws. Solution methods and tools to that multi-equation system are also available[16]. A drawback of the volume average approach is that the discrete nature (morphology of each individual crystal, size distribution of the solidified crystals or included particles and gas bubbles) of each single phase is neglected. Therefore, the interactions between phases must be approximately based on the averaging theory to characterize the properties of the phases. The major challenges for a particular solidification model lie on the following aspects:① Mathematical descriptions of the source terms and interphase exchange terms based on the hydrodynamics, solidification thermodynamics and diffusion kinetics which occur at the microstructure scale; ②Numerical complexity of the coupled multi-equation system with the increasing number of involved phases; ③ Limitation of the computational capacity.

As an example shown in Fig.1, too many phases are involved in one system: the liquid melt, the solids (columnar and equiaxed are considered as separated phases), the gas bubbles, the pores (might be considered as different phase from the gas bubbles), the non-metallic inclusions or slag. It is not possible to take all the phases into account in one model. Therefore, most solidification models, recently applicable for the calculation of macrosegregation of industry ingots, are limited to 2～3 phases. They are summarized in Table 1.

The most advanced model is the 5-phase dendritic mixed columnar-equiaxed solidification model, but the extreme calculation cost has prevented it from the application for large castings. For the moment, most applications are based on the one-phase mixture solidification model[17-30], or two-phase model considering stationary solid (columnar) or moving solid (equiaxed)[5, 39-47]. In order to consider both columnar and equiaxed phases simultaneously, a model considering at least 3 phases[48-52]must be used. A compromise has to be made between the complexity of the model and the limitation by the computational capacity. In the following section, examples of different macrosegregation phenomena occurred typically in ingot castings are analyzed by the numerical models.

2Modelling examples

2.1Thermosolutal convection-induced macrosegregation

A two-phase columnar (cylindrical morphology) solidification model is used to study the formation of macrosegregation caused by thermosolutal convection. Key features of this model are summarized in Table 1, and details can refer to previous publications[39-47].A benchmark ingot (φ66 mm×170 mm)of Fe-0.34 wt%C alloy is simulated. For this study some further simplifications are made: mould filling is ignored, solidification starts with an initial concentration Fe-0.34 wt%C and an initial temperature of 1785 K; solidification shrinkage is not considered, a Boussinesq approximation is used to treat thermosolutal convection, and the thermal and solutal expansion coefficients of the melt are βT=2×10-4K-1, βc=0.011wt%-1, respectively;2D axis symmetric calculations are carried out.

The predicted solidification sequence and evolution of macrosegregation are shown in Fig.2. The columnar tip front and volume fraction of the columnar phase (fc-isolines)move from the outer region towards the bulk melt region. Due to thermosolutal convection, the ‘hot spot’ in the ingot centre moves upwards and is finally located slightly above the geometrical centre of the casting. During solidification an axis symmetric convection pattern develops. The melt near the mould wall has a higher density due to its lower temperature, and thus sinks downwards, while the hotter melt in the centre rises. One may argue that the solute-enriched, lower density interdendritic melt might rise and thus partially compensate or reverse the above mentioned convection pattern. However, with the given temperature gradient, the thermal buoyancy dominates over the solutal buoyancy. The downward flow near the columnar tip region and the upward flow in the bulk melt are the primary phenomena which lead to the final macrosegregation. Here the macrosegregation is evaluated with a macrosegregation index, being calculated as100×(cmix-c0)/c0, wherecmixis the liquid-solid mixture concentration. The final macrosegregation map (Fig.2e)shows: a small region with negative macrosegregation is found in the upper surface region, particularly in the upper corners (-0.9%). In the lower corners a positive macrosegregation is predicted (+5.9%). A large area of positive macrosegregation (+11.7%) is located in the casting centre.

The macrosegregation mechanism during columnar solidification due to thermosolutal convection can be analysed as follows. With the assumption of stationary solid and no solidification shrinkage, the evolution of the mixture concentration in mushy zone can be expressed as:

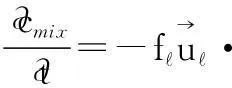
(1)

The evolution of cmixis a function of the scalar product of the flux of the interdendritic melt flow fand the gradient of the liquid concentrationc. If both vectors fandcpoint in the same directions (the angle between the two vectors is smaller than 90°), cmixtends to decrease (∂cmix/∂t<0). As shown in Fig.3, this mechanism acts in the upper corner region of the ingot. Both the melt flow and the liquid concentration gradient have almost the same direction. In the other words, solute-poor melt replaces the solute-rich melt in this region, and thus, leads to a reduction of cmix(or formation of negative segregation). In the opposite situation, if both vectors fandcpoint in the opposite directions (the angle between the two vectors is larger than 90°), cmixtends to increase (∂cmix/∂t>0). As shown in Fig.3, this mechanism acts in the lower corner region of the ingot. In the other words, the melt leaving the region has a relative lower concentration than the melt which will feed the region. It leads to an increase of cmix(or formation of positive segregation). Please notice that Eq.(1) applies only if solidification shrinkage induced flow can be ignored.

Fig.3　Analysis of the formation of macrosegregation in the initial stage. Here only corner regions are investigated. The liquid concentration c is shown by the gray scale with dark for the highest concentration and light for the lowest concentration. The black arrows indicate the direction of the melt flow , whereas the white arrows indicate the direction of the liquid concentration gradient c

The positive macrosegregation in the ingot centre (Fig.2) is formed gradually during solidification. As mentioned above, the interdendritic melt has a higher concentration than the bulk melt. The interdendritic solute-enriched melt is brought out of the mushy zone by the flow, causing cmixin front of or slightly behind the columnar tip front to be enriched gradually. These positively enriched melts are not stationary, they move with the flow, and finally meet in the casting centre and form a large positive segregation zone.

2.2Sedimentation-induced macrosegregation

Here the same benchmark ingot as 2.1 is simulated, but now with the assumption of globular equiaxed solidification. The purpose is to study the formation of macrosegregation by the mechanism of grain sedimentation and sedimentation-induced convection during equiaxed solidification. Key features of the two-phase globular equiaxed solidification model are summarized in Table 1, and details can refer to previous publications[14, 31-38].Further simplifications are: mould filling is ignored;solidification shrinkage is not considered, a Boussinesq approximation is used to treat the buoyancy force for the grain sedimentation, and liquid and solid densities are 7 027 kg·m-3, 7 321 kg·m-3, respectively; 2D axis symmetric calculations are carried out; additionally, a heterogeneous nucleation law is used to model the origin of equiaxed crystals with following parameters:nmax=1×1011m-3,ΔTσ=4K,ΔTN=10K.

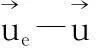
Fig.4　Predicted solidification sequence and formation of macrosegregation induced by grain sedimentation. The volume fraction of equiaxed grains fe is shown in gray-scale (light forfe=0 and dark forfe = 1), and overlaid with the equiaxed velocity e, melt velocity , and the relative velocity . The distribution of cmix is also shown in gray-scale. The macrosegregation index, as calculated as 100×(cmix-c0)/c0, is shown. The final macrosegregation map is almost identical to the one at 67 s

The relative motion between the equiaxed grains and the melt results in the formation of macrosegregation. The evolution of the mixture concentration in mushy zone can be expressed as:

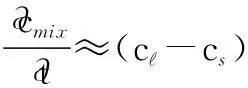
(2)

As shown in Fig.4, in the initial stage the solute-poor grains at the top corner regions sink and solute-enriched melt is drawn into the corners, causing positive segregation, i.e. the mechanism shown in Fig.5a operates. At the bottom corners, the solute-poor grains settle and ‘squeeze’ the solute-enriched melt out of the corners, causing negative segregation, i.e. shown in Fig.5b. However, at the top corners the positive segregation zones are actually not stationary. They move downwards along the wall and then move slowly away from the wall towards the casting centre. This is due to the fact that the positive segregation zones are associated with fluid and thus may move with melt convection. As visible in Fig.4b-c, along the casting top surface the melt flows continuously into the corner and thus develops a local circulation current, causing a motion of the positive segregation region. The positive segregated area, as it moves, becomes wider and wider. The equiaxed grains continue to grow, sink, and eventually leave the enriched melt behind. While sedimentation goes on, the bottom negative segregation zone becomes larger and larger as well. The grains pile-up slowly, creating a relatively large negative segregation zone at the bottom. Due to the coupling of melt flow and grain movement, the cmixfield is slightly modified in the last stage of solidification. However, the primary mechanism responsible for negative segregation at the bottom of the casting is due to mechanism as shown in Fig.5b.

Fig.5　Macrosegregation formation mechanisms (k<1) by grain sedimentation: (a)negative segregation formed by replacing the solute rich melt with solute poor grains, and (b) positive segregation formed by replacing the solute poor grains with solute rich melt

2.3Segregation in a 2.45-ton steel ingot

A three-phase mixed columnar-equiaxed solidification model is used to study the formation of macrosegregation in an industry ingot. Key features of the model are summarized in Table 1, and details can refer to previous publications[48-52].The experimentally measured macrosegregation of a 2.45 ton big-end-up ingot (Fe-0.45 wt%C) was reported[1]. The ingot had a section of square and was cast in a chilled mold. The segregation in this ingot is numerically simulated, as shown in Fig.6. The sulphur print of this ingot is shown in Fig.6a. The measured segregation index (100×(cmix-c0)/c0) map is shown in Fig.6b. Configuration of this ingot, together with necessary boundary and initial conditions used for the calculation, is described in Fig.6c. More details about the simulation configurations are presented elsewhere[52]. 2D axis symmetrical simulations are performed to approximate the solidification behaviour in the square section ingot. The predicted solidification sequence is shown in Fig.7 and the segregation map is shown in Fig.6d.

Fig.6　Configuration of a 2.45-ton industry-scale steel ingot: (a) experimental ingot and (b) experimentally measured segregation [1], (c) simulation settings and (d) simulated macrosegregation in grey scale ( black for the positive segregation and light for the negative segregation) overlapped with isolines. The macrosegregation, both experimental (b) and simulated (d), is shown for the segregation index (100×(cmix-co)/co). Nucleation parameters for equiaxed crystals: nmax=5×109m-3, ΔTσ=2 K,ΔTN=5 K

The global solidification sequence in this 2.45 ton ingot is shown in Fig.7. The sinking of the equiaxed crystals in front of the columnar dendrite tips leads to an accumulation of equiaxed phase in the base region of the ingot. The accumulation of the equiaxed phase in the base region will block the growth of the columnar dendrite tips, i.e. columnar-to-equiaxed transition (CET) occurs there, hence finally to cause a characteristic cone-shape distribution of equiaxed zone being enveloped in the CET line. Relatively strong negative segregation is predicted in the low-bottom equiaxed zone. With the sedimentation of large amount of equiaxed crystals downwards, the solute enriched melt is pushed upwards in the casting centre, hence to cause a positive segregation in the upper region. Some other interesting phenomena occurred in such industry ingot are analysed below.

Firstly, the flow is instable (Fig.7). The melt flow in the bulk region ahead of the columnar dendrite tip front is driven by three mechanisms: the solutal buoyancy driving upwards; the thermal buoyancy driving downwards; and the equiaxed sedimentation which drags the surrounding melt downwards. Generally the two downward driving forces dominate, and the melt flows downwards along the columnar dendrite tip front. This downward flow along the columnar tips will push the melt to rise in the ingot centre. This rising melt will interact with the falling equiaxed crystals and with the downward flow near the columnar tip front, to form many local convection cells. The pattern of melt convection and crystal sedimentation becomes chaotic. These local convection cells are developed or suppressed dynamically, and the flow direction in the cells changes with time as well. The flow instability and the flow chaotic behaviour are dependent on the ingot size (ingot height).

Fig.7　Solidification sequence of the 2.45 ton ingot. The volume fraction of each phase (fe or fc) is shown in gray scale from minimum (bright) to maximum (dark). The left half of each figure shows the evolution of equiaxed volume fraction (fe) together with the equiaxed sedimentation velocity e) in black arrows. The right half of each figure shows the evolution of columnar volume fraction (fc) together with the melt velocity) in black arrows. The columnar dendrite tip position also marked with a black solid line

Secondly, a streak-like segregation pattern (Fig.6d) in the mixed columnar-equiaxed region is predicted. Concrete explanation to this segregation pattern demands more detailed analysis of the flow and sedimentation and their interaction with the solidification, nevertheless a tentative hypothesis is proposed as follows. As the equiaxed crystal can be captured (crystal entrapment) by the growing columnar trunks, the entrapment of the equiaxed crystals will lead to a heterogeneous, i.e. streak-like, phase distribution between the columnar and equiaxed immediately behind the columnar tip front, as seen in Fig.7b-d. The resistance to the interdendritic flow by the columnar trunks and the entrapped equiaxed crystals are different; therefore the flow direction of the melt in this region is slightly diverted by the heterogeneous phase distribution. This diverted-flow can only be visible in the carefully zoomed view. As the macrosegregation is extremely sensitive to the interdendritic flow, it is not surprising that the induced macrosegregation (Fig.6d) takes the similar streak-like pattern of the phase distribution (Fig.7d).

One may notice that this streak-like segregation has a similar contour as the classical A-segregation, but it is still not clear if the classical A-segregation is the same one as the streak-like segregation or originates from such streak-like segregation. According to the mostly-accepted empirical explanation, A-segregation belongs to a kind of channel segregation in large steel ingots, which originates and develops in the stationary dendritic mushy zone. A recent study of the authors[46-47]in a Sn-Pb laboratory casting has found that the channel segregation can originate and develop in a pure columnar solidification, where no equiaxed crystal exists. Therefore, we name the streak-like segregation here as a quasi-A-segregation. To form this quasi-A-segregation, the sedimentation of equiaxed crystals and its interaction with the columnar tip front and melt flow seem to play important role.

Thirdly, the simulation of the 2.45 ton ingot shows an isolated hot spot in the upper part (Fig.7d), which takes much long time to solidify. As the middle part of the ingot is already blocked by the columnar trunks, the solidification of the hot spot behaves like a mini-ingot. Sedimentation of the equiaxed crystals in the mini-ingot will cause a small region of negative segregation, as shown in Fig.6d. This kind phenomenon happens very often in long (small section) ingot casting or in the continuously-cast round billet casting, and it is called as ‘bridging and mini-ingotism’[64]. The experimental result of Fig.6b seems to show that no such ‘bridging and mini-ingotism’ occurs, as no such negative segregation zone is identified. It implies that the heat transfer boundary conditions applied in the current simulation might not be coincident with the reality.

The segregation along the ingot centreline is analysed, and compared with the experiment, as shown in Fig.8. The experiment shows the negative segregation in the lower part and positive segregation in the upper part. The model also shows the same tendency. They agree with each other qualitatively. However, the negative segregation in the lower part is predicted more severe than the experimental result. The overestimation of the negative segregation in the lower part by the model may come from two aspects. One is the assumption of globular equiaxed morphology, which can cause significant overestimation of the sedimentation-induced negative segregation. The real equiaxed crystals are mostly dendritic. The other aspect is the error assumption of the equiaxed nucleation parameters.

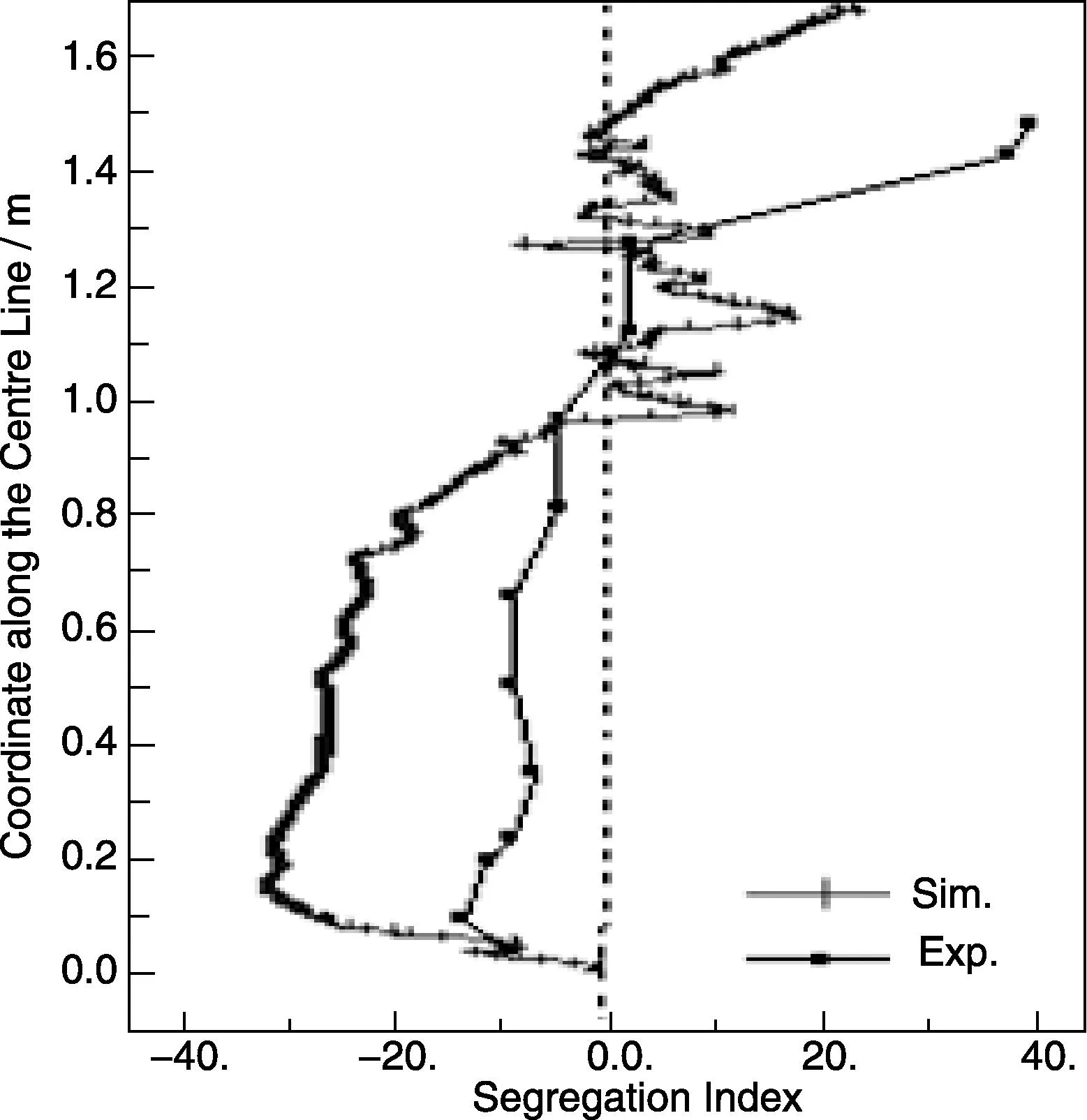
Fig.8　Comparison of the numerically predicted macrosegregation (100×(cmix-co)/co) along the ingot centreline with the experiment[1]. Nucleation parameters for equiaxed:nmax=5×109m-3, ΔTσ=2 K, ΔTN=5 K

2.4Dendritic solidification of an Al-4wt%Cu ingot

Fig.9　An example of the modelling result of an Al-4 wt%Cu ingot with a five-phase mixed columnar-equiaxed solidification model with dendritic morphology: (a) comparison of the measured (spark analysis) macrosegregation (left half) with the calculated one (right half), the casting is poured at 800 ℃, here the segregation index (100×(cmix-co)/co)is shown in grey scale (dark for the most positive and light for the most negative segregation), CET positions are plotted; This numerical simulation result shows satisfactory agreement with the as-cast macrostructure: (b) macrograph and (c) micrograph

The three-phase model used in 2.3 does not consider dendritic morphology. This deficiency has overestimated the cone of the negative segregation at the base of the ingot, like what we see in Fig.6 and 8. In order to consider the dendritic morphology, more phases (or phase regions), i.e. the interdendritic melt, must be separately considered. The interdendritic melt in the equiaxed grain, highly enriched with solute, is entrapped in the crystal envelope, moving likely in the same velocity as the equiaxed grain. A five-phase model was developed by the group of authors to consider the mixed columnar-equiaxed solidification with dendritic morphology[60-63]. The calculation expense is so high as to prevent application in industry ingots. The validity of this model for such a purpose has been verified, but in a laboratory Al-4.0 wt%Cu ingot casting, as shown in Fig.9. A cylindrical casting (φ75 mm×133 mm) was poured and was analysed for both macrostructure and macrosegregation. Some key features of the segregation maps agree with each other: ① the measured concentration index falls in a range between -8.0%～7.8 % compared to a predicted range of -6.5%～9.8 %; ② the upper region of the ingot has negative xmacrosegregation; ③ the equiaxed core of the ingot exhibits an extreme negative macrosegregation;④ the mixed columnar/equiaxed zone at top boundary of the CET line exhibits positive macrosegregation; ⑤ the bottom boundary of CET contains dispersed regions of positive macrosegregation; ⑥ the mixed columnar/equiaxed structure between CET and mold wall is positively segregated and ⑦ several discrete sites of positive and negative macrosegregation exist in the upper part of the ingot.

3Discussions

Based on the review of the last-century research progress in the modelling of macrosegregation, Beckermann has summarized 5 basic phenomena which are worthy increasing research attention[10]:① macrosegregation in presence of grain structure transition (e.g. columnar to equiaxed, namely CET); ② macrosegregation due to movement of solid; ③ macrosegregation in multicomponent alloys, taking into account the formation of multiphases; ④ macrosegregation due to deformation of the solid and mush; ⑤ micro-/macrosegregation in the presence of undercooled, convecting liquid. The modelling examples presented in the current article have demonstrated that by introducing the multiphase computational fluid mechanics (MCFD) the phenomena ① and ② can be well treated. A previous work of the authors[65-66]has shown that the MCFD-based solidification model can be extended to cover multicomponent alloy (phenomenon 3) and to couple the micro- and macrosegregation in the presence of undercooled and convecting liquid (phenomenon 5). Some efforts were done to treat the deforming mushy zone (phenomenon 4), a key phenomenon for understanding the centreline macrosegregation in continuously cast slab casting[43-45]. Potentials and limitations of the MCFD-based solidification models for the as-cast structure and macrosegregation in ingot castings are summarized and discussed as follows.

3.1Model potentials

(1)The typical mixed columnar-equiaxed solidification sequence including the sedimentation of the equiaxed crystals, the growth of the columnar tip front and the formation of the final as-cast structure with CET can be simulated.Accurate solutions to the multiphase flow dynamics and interactions among the melt, equiaxed crystals and growing columnar trunks are very important steps for modelling the typical as-cast structure and segregation pattern.

(2)The most typical segregation, the concentrated positive segregation under hot-top and the cone of negative segregation at the base of the ingot, can be simulated. The simulated cone of negative segregation by equiaxed crystal sedimentation seems to have reproduced the experimental phenomenon, which has been understood by metallurgists[67]: “The heap of equiaxed grains at the base of the ingot has a characteristic cone shape. Because it is composed of dendritic fragments, its average composition is that of rather pure iron, having less solute than the average for the ingot.” Mechanisms for positive segregations under the hot-top in steel ingots are diverse. It is generally agreed that they are caused by the melt convection in the bulk region or the partially solidified and/or re-melted mushy zone. For example, the upper positive segregation is explained by the melt convection in the bulk region, because the light solute-enriched melt rises. According to the recent modelling results, with the sedimentation of a large amount of equiaxed crystals downwards, the relatively positive segregated melt is pushed upwards, instead of ‘rising’ by itself, in the casting centre, hence causing a positive segregation zone in the upper region.

(3)The ability to calculate the columnar-to-equiaxed transition (CET) has been demonstrated. The upper region of the ingot mainly consists of columnar dendrites, whereas a larger amount of equiaxed grains are predicted in the base region. Within the CET enclosed region, only the equiaxed phase exists, while outside of the CET region both columnar and equiaxed phases coexist.

(4)Although the capability of the current models for the interdendritic-flow-induced channel segregation has been shown in previous publications[46-47], it was not clearly shown in the above examples. The modelling result for the channel segregation is extremely sensitive to the grid resolution. Grid size less than 0.1 mm is often required, and this is unrealistic for the large industry ingots on the basis of the current computer resources. One interesting finding by the current MCFD-based solidification model, worth mentioning here, is the streak-like (quasi-A) segregation pattern, which occurs in such large ingots and is strengthened by the columnar-equiaxed interaction at the columnar tip front. The streak-like segregation pattern has some similarity to the classical A-segregation, but it is not clear if the classical A-segregation is the same as or whether it originates from the streak-like segregation. This is still to be verified.

3.2Limitation of the models

The importance of the applied process conditions, e.g. the pouring temperature, pouring method, mould materials and interfacial heat transfer between the ingot and the mould, etc., for the quantitative accuracy of the simulated solidification process and, hence, for the accuracy of the macrosegregation is obvious. It is not discussed here. Following discussions focus on the aspect of numerical models.

The influence of the nucleation event on macrosegregation was addressed in the example of the 2.45-ton ingot. The origin of the equiaxed grains may be due to different mechanisms, e.g. heterogeneous nucleation, and/or fragmentation and detachment of dendrites by re-melting, and/or nucleation formed during pouring by contact with the initial chilling of the mould. The recent models condense all of these phenomena into a single effective nucleation description. Here, a three-parameter heterogeneous nucleation law[14]is applied for the origin of equiaxed crystals. It is only possible to obtain the reliable nucleation parameters experimentally.

No shrinkage cavity and porosity are considered. This deficiency will influence the accuracy of the calculation, especially in the hot-top region. As shrinkage contributes to or influences the interdendritic flow, it will also influence the final distribution of the channel segregation. However, the global segregation pattern, e.g., the concentrated positive segregation in the upper region and the cone of negative segregation at the base of the ingot, will not be significantly influenced by the shrinkage.

No thermal mechanics is considered. The thermal mechanical shrinkage of the solidified outer shell of the ingot will influence the internal flow, but this may not be particularly significant. What is the most important is the deformation of the growing crystals due to the thermal shrinkage or the solid phase transition, which would have great impact on the flow near the end of solidification at the central cone region. The ‘V’ segregation is very much related to this kind of deformation. This ‘V’ segregation is not modelled currently.

One drawback of the MCFD-based solidification models is the high computational demand. An example of 2.45-ton ingot (Section 2.3) took 2 weeks of the calculation on an 8-core cluster (Intel Nehalem Cluster 2.93 GHz,operated in year 2009). The computational expense increases correspondingly with the increasing of ingot size. It means that application of the MCFD-based solidification models still depends on the further development of computational resources.

4Outlook

The future modelling activities for macrosegregation in ingot castings will progress in two directions. One is to further enhance the model capability and accuracy by including more physical phenomena such as formation of cavity and porosity due to solidification shrinkage, thermal mechanical deformation, dendrite fragmentation, etc. Another direction is to further validate and improve the existing multiphase models, and to apply them for the purpose of interpreting engineering phenomena and enhancing fundamental understanding of different segregation mechanisms.

(1)Thanks to the work of the Iron Steel Institute[1], many steel ingots scaled from 600 kg to 172 tons were poured and sectioned for segregation analysis. This work provides most valuable information for the validation of the numerical models. Although many process parameters for those ingots were not well documented and have to be assumed, the capability to reproduce segregation patterns of all (most) those ingots numerically is an important step for the development of macrosegregation models.

(2) Numerical study of casting parameters based on the existing models enhances the knowledge of metallurgists about macrosegregation. Despite the difficulty of quantitatively reproducing the segregation pattern of reality, the influence of the process parameters, such as casting geometry, mould materials, pouring temperature, and other engineering measures on segregation can be described numerically. By performing this kind of parameter study, metallurgists would acquire valuable knowledge for process optimization.

(3) Any segregation mechanism, as proposed from experimental observation, can (should) be verified quantitatively by the mathematical (numerical or analytical) models. The multiphase model can help to explain many well-known segregation phenomena in detail. It may also help to explore the new segregation phenomena, which are caused by the multiphase flow. For example, the question of streak-like segregation (Section 2.3), here referred to as quasi-A-segregation, is raised on the basis of the current modelling exercise. The equiaxed-columnar interaction at the columnar dendrite tip front and its influence on the melt flow seem to induce or enhance this kind of a streak-like macrosegregation.

(4)Some more fundamental issues as Beckermann pointed out[10]have surely impact on the modelling of the as-cast structure and macrosegregation: ① nucleation in a convective environment; ② fragmentation and transport of fragments originating in the mushy zone or at outer surfaces; ③ effects of flow on the growth rates of the dendrite tips, eutectic front, etc.; ④ effects of flow on the evolution of dendrite arm spacings and other microstructural length scale; ⑤ two phase rheology of melt laden with equiaxed grains. Solutions to all those issues rely on not only the efforts of numerical modellers, but also raise some new research topics for scientists in the field of solidification.

References

[1]Iron Steel Institute. Report on the Heterogeneity of Steel Ingots[J].JIronSteelInstitute, 1926,103: 39-151.

[2]Iron E Marburg. Accelerated Solidification in Ingots: Its Influence on Ingot Soundness[J].JMet, 1953,5: 157-172.

[3]Kajikawa K, Suzuki S, Takahashi F,etal. Development of 650-ton-Class Ingot for Turbine Rotor Shaft Forging Application[C]//Proceedingsofthe1stIntConfIngotCasting,RollingandForging,Session-IngotCastingTechnology. Aachen: 2012: 1-6.

[4]Wang J, Fu P, Liu H,etal. Shrinkage Porosity Criteria and Optimized Design of a 100-ton 30Cr2Ni4MoV Forging Ingot[J].MaterDesign, 2012,35: 446-456.

[5]Combeau H, Zaloznik M, Hans S,etal. Prediction of Macrosegregation in Steel Ingot: Influence of the Motion and the Morphology of Equiaxed Grains[J].MetallMaterTrans, 2009,40B: 289-304.

[6]Lesoult G. Macrosegregation in Steel Strands and Ingots: Characterization, Formation and Consequences[J].MaterSciEngA, 2005,413-414: 19-30.

[7]Flemings M C, Nereo G E. Macrosegregation-Part I[J]. TMS-AIME, 1968,239: 1 449-1 461.

[8]Flemings M C. Our Understanding of Macrosegregation: Past and Present[J].ISIJInt, 2000,40: 833-841.

[9]Moore J J , Shah N A. Mechanisms of Formation of A- and V-Segregation in Cast Steel[J].IntMetalsRev, 1983,28: 338-356.

[10]Beckermann C. Modelling of Macrosegregation: Applications and Future Needs[J].IntMaterRev, 2002,47: 243-261.

[11]Pickering E J. Macrosegregation in Steel Ingots: the Applicability of Modelling and Characterisation Techniques[J].ISIJInt, 2013,53: 935-949.

[12]Voller V. A Multi- Scale/Multi-Physics Modeling Framework for Solidification Systems[C]//Proceedingsof5thInternConfonCFDintheProcessIndustries, CSIRO. Melbourne: 2006: 1-4.

[13]Boettinger W J, Coriell S R, Greer A L,etal. Solidification Microstructure: Recent Developments, Future Directions[J].ActaMater, 2000,48: 43-70.

[14]Rappaz M. Modelling of Microstructure Formation in Solidification Processes[J].InternMaterRev, 1989,34: 93-123.

[15]Beckermann C, Viskanta R. Mathematical Modeling of Transport Phenomena during Alloy Solidification[J].ApplMechRev, 1993,46: 1-27.

[16]M. Wu. Eulerian Multiphase Modelling of Solidification Processes, Habilitationsschrift, University of Leoben, 2007.

[17]Bennon W D, Incropera F P. A Continuum Model for Momentum, Heat and Species Transport in Binary Solid-Liquid Phase Change Systems-I. Model Formulation[J].IntJHeatMassTransfer, 1987,30: 2 161-2 170.

[18]Vreeman C J, Krane M J M, Incropera F P. The Effect of Free-Floating Dendrites and Convection on Macrosegragation in Direct Chill Cast Aluminum Alloys-I: Model Development[J].IntJHeatMassTransfer, 2000,43: 677-686.

[19]Voller V R, Prakash C. A Fixed Grid Numerical Modelling Methodology for Convection-Diffusion Mushy Region Phase-Change Problems[J].IntJHeatMassTransfer, 1987,30:1 709-1 719.

[20]Voller V R, Brent A D, Prakash C. The Modelling of Heat, Mass and Solute Transport in Solidification Systems[J].IntJHeatMassTransfer, 1989,32: 1 719-1 731.

[21]Voller V R, Brent A D, Prakash C. Modelling the Mushy Region in a Binary Alloy[J].ApplMathModeling, 1990,14: 320-326.

[22]Voller V R, Swaminathan C R. General Source-Based Method for Solidification Phase Change[J].NumericalHeatTransfer,PartB,1991,19: 175-189.

[23]Prescott P J, Incropera F P. The Effect of Turbulence on Solidification of a Binary Metal Alloy with Electromagnetic Stirring[J].TranspPhenomenainMaterProcManufacturing,ASMEHTD, 1994 ,280 : 59-69.

[24]Prescott P J, Incropera F P. Convective Transport Phenomena and Macrosegregation during Solidification of a Binary Metal Alloy-I: Numerical Predictions[J].JHeatTransfer, 1994,116 : 735-741.

[25]Prescott P J, Incropera F P, Gaskell D R. Convective Transport Phenomena and Macrosegregation during Solidification of a Binary Metal Alloy-II: Experiments and Comparisons with Numerical Predictions[J].JHeatTransfer, 1994,116 : 742-749.

[26]Nadella R, Eskin D, Du Q,etal. Macrosegregation in Direct-Chill Casting of Aluminium Alloys[J].ProgMaterSci, 2008,53:421-480.

[27]Gu J P, Beckermann C. Simulation of Convection and Macrosegregation in a Large Steel Ingot[J].MetallMaterTransA, 1999,33 : 1 357-1 366.

[28]Thomas B G, Malley R O, Stone D. Measurement of Temperature, Solidification, and Microstructure in a Continuous Cast Thin Slab[C]//McWASP-VIII,TMSProceedings. 1998: 1 185-1 199.

[29]Krane M, Incropera F, Gaskell D. Solidification of Ternary Metal Alloys-I. Model Development[J].IntJHeatMassTransfer, 1997,40 : 3 827-3 835.

[30]Schneider M, Beckermann C. Formation of Macrosegregation by Multicomponent Thermosolutal Convection during the Solidification of Steel[J].MetallMaterTransA,1995, 26: 2 373-2 388.

[31]Beckermann C, Viskanta R. Mathematical Modeling of Transport Phenomena during Alloy Solidification[J].ApplMechRev, 1993,46 : 1-27.

[32]Ni J, Beckermann C. A Volume-Averaged Two-Phase Model for Transport Phenomena during Solidification[J].MetallMaterTransB, 1991,22 : 349-361.

[33]Ludwig A, Wu M. Modeling of Globular Equiaxed Solidification with a Two-Phase Approach[J].MetallMaterTransA, 2002,33:3 673-3 683.

[34]Wu M, Ludwig A, Bührig-Polaczek A,etal. Influence of Convection and Grain Movement on Globular Equiaxed Solidification[J].IntJHeatMassTransfer, 2003,46 : 2 819-2 832.

[35]Wu M, Ludwig A, Bührig-Polaczek A. Grain Sedimentation and Melt Convection Phenomena during Globular Equiaxed Solidification[M]// Dieter M.SolidificationandCrystallization, eds. Weinheim: Wiley-VCH Verlag GmbH & Co. KGaA, 2004: 204-212.

[36]Wu M, Ludwig A. Influence of Phase Transport Phenomena on Macrosegregation and Structure Formation during Solidification[J].AdvEngMater, 2003,5 : 62-66.

[37]Wang T, Yao S, Zhang X,etal. Modelling of the Thermo-Solutal Convection, Shrinkage Flow and Grain Movement during Globular Equiaxed Solidification in a Multi-Phase System-I. Three-Phase Flow Model[J].ActaMetallurgicaSinica, 2006,42 :584-590.

[38]Wu M, Ludwig A, Luo J. Numerical Study of the Thermal-Solutal Convection and Grain Sedimentation during Globular Equiaxed Solidification[J].MaterSciForum, 2005,475-479 : 2 725-2 730.

[39]Miyazawa K, Schwerdtfeger K. Macrosegregation in Continuously Cast Steel Slabs-Preliminary Theoretical Investigation on the Effect of Steady-State Bulging[J].ArchEisenhüttenwes, 1981,52 : 415-422.

[40]Kajitani T, Drezet J M, Rappaz M. Numerical Simulation of Deformation-Induced Segregation in Continuous Casting of Steel[J].MetallMaterTransA, 2001,32: 1 479-1 491.

[41]Combeau H, Michel B, Fautrelle Y,etal. Analysis of a Numerical Benchmark for Columnar Solidification of Binary Alloys[M]//IOPConferenceSeriesMaterialsScienceandEngineering.2012.

[42]Wu M, Könözsy L, Ludwig A,etal. On the Formation of Macrosegregation in Steel Ingot Castings[J].SteelResInt, 2008,79 : 637-644.

[43]Mayer F, Wu M, Ludwig A. Study of Centreline Macrosegregation in Steel Continuous Casting with a Two-Phase Volume Averaging Approach[C]. TMS,2009:279-286.

[44]Mayer F, Wu M, Ludwig A. Formation of Centreline Segregation in Continuous Slab Casting of Steel due to Bulging and/or Feeding[J].SteelResInt, 2010,81: 660-667.

[45]Wu M, Domitner J, Ludwig A. Using a Two-Phase Columnar Solidification Model to Study the Principle of Mechanical Soft Reduction in Slab Casting[J].MetallMaterTransA, 2012,43:945-963.

[46]Li J, Wu M, Hao J,etal. Simulation of Channel Segregation Using a Two-Phase Columnar Solidification Model, Part I: Model Description and Verification[J].CompMaterSci, 2012,55: 407-418.

[47]Li J, Wu M, Hao J,etal. Simulation of Channel Segregation Using a Two-Phase Columnar Solidification Model, Part II: Mechanism and Parameter Study[J].CompMaterSci, 2012,55: 419-429.

[48]Wu M, Ludwig A. Study of Spatial Phase Separation during Solidification and Its Impact on the Formation of Macrosegregation [J].MaterSciEngA, 2005,413-414: 192-199.

[49]Wu M, Ludwig A. A 3-Phase Model for Mixed Columnar-Equiaxed Solidification[J].MetallMaterTransA, 2006,37: 1 613-1 631.

[50]Wu M, Ludwig A. Using a Three-Phase Deterministic Model for the Columnar-to-Equiaxed Transition (CET) [J].MetallMaterTransA, 2007,38: 1 465-1 475.

[51]Wu M, Li J, Kharicha A,etal. Using a Three-Phase Mixed Columnar-Equiaxed Solidification Model to Study Macrosegregation in Ingot Castings: Perspectives and Limitations[M]//Proceedingsofthe2013InternationalSymposiumonLiquidMetalProcessingandCasting. John Wiley & Sons, Inc., 2013.

[52]Li J, Wu M, Kharicha A,etal. The Predication of Macrosegregation in a 2.45 ton Steel Ingot with a Mixed Columnar-Equiaxed Three Phases Model[J].IntJHeatandMassTransfer, 2014,72: 668-679.

[53]Rappaz M, Thévoz Ph. Solute Diffusion Model for Equiaxed Dendritic Growth[J].ActaMetall, 1987,35: 1 487-1 497.

[54]Rappaz M, Thévoz Ph. Solute Diffusion Model for Equiaxed Dendritic Growth-Analytical Solution[J].ActaMetall, 1987,35: 2 929-2 933.

[55]Wang C Y, Beckermann C. A Multiphase Solute Diffusion Model for Dendritic Alloy Solidification[J].MetallTransA, 1993,24:2 787-2 802.

[56]Wang C Y, Beckermann C. Equiaxed Dendritic Solidification with Convection: Part 1. Multi-Scale /-Phase Modeling[J].MetallMaterTransA, 1996,27: 2 754-2 783.

[57]Nielsen, Appolaire B, Combeau H,etal. Measurements and Modelling on the Microstructural Morphology during Equiaxed Solidification of Al-Cu Alloys[J].MetallMaterTransA, 2001,32: 2 049-2 060.

[58]Wu M, Ludwig A. Modeling Equiaxed Dendritic Solidification with Melt Convection and Grain Sedimentation, Part I: The Model[J].ActaMater, 2009,57: 5 621-5 631.

[59]Wu M, Ludwig A. Modeling Equiaxed Dendritic Solidification with Melt Convection and Grain Sedimentation, Part II: The Results and Verifications[J].ActaMater, 2009,57: 5 632-5 644.

[60]Wu M, Fjeld A, Ludwig A. Modeling Mixed Columnar-Equiaxed Solidification with Melt Convection and Grain Sedimentation-Part I: Model Description[J].CompMaterSci, 2010,50: 32-42.

[61]Wu M, Fjeld A, Ludwig A. Modeling Mixed Columnar-Equiaxed Solidification with Melt Convection and Grain Sedimentation-Part II: Illustrative Modeling Results and Parameter Studies[J].CompMaterSci, 2010,50: 43-58.

[62]Wu M, Ludwig A. An Idea to Treat the Dendritic Morphology in the Mixed Columnar-Equiaxed Solidification[J].IntJCastMetalsResearch, 2009,22: 323-327.

[63]Ahmadein M, Wu M, Li J,etal. Prediction of the As-Cast Structure of Al-4.0 wt.% Cu Ingots[J].MetallMaterTransA, 2013,44: 2 895-2 903.

[64]Moore J J. Review of Axial Segregation in Continuously Cast Steel[J].IronandSteelSoc, 1984,3: 11-20.

[65]Wu M, Li J, Kharicha A,etal. Modeling Diffusion-Governed Solidification of Ternary Alloy-I: Coupling Solidification Kinetics with Thermodynamics[J].CompMaterSci, 2013,79: 830-840.

[66]Wu M, Li J, Kharicha A,etal. Modeling Diffusion-Governed Solidification of Ternary Alloy-II: Macroscopic Transport Phenomena and Macrosegregation[J].CompMaterSci, 2014,92: 267-285.

[67]Campbell J.Castings[M]. Butterworth Heinemann Ltd., 1991

(编辑惠琼)

Received date：2014-10-09

Corresponding author：Wu M,Born in 1963，Professor，Email: menghuai.wu@unileoben.ac.at

吴孟怀1,2, Kharicha A1,2, Ludwig A2

(1． Christian-Doppler Laboratory for Advanced Process Simulation of Solidification & Melting,

University of Leoben, A-8700 Leoben, Austria)

(2．Department of Metallurgy, University of Leoben, A-8700 Leoben, Austria)

摘要：自1960s Flemings 时代起人们经过半个世纪的努力已对铸锭内铸态组织和宏观偏析形成的物理机理有了定性或半定量的认识，但还是难以对其进行定量预测，主要原因是其与各种多相流现象有关，例如凝固糊状区枝晶间的对流，等轴晶区晶粒沉积等。当然这些多相流现象是与凝固过程热力学和扩散动力学以及宏观铸态组织形成过程相耦合的。近20年多相计算流体动力学的发展及其在凝固领域的应用为解决上述问题提供了有效手段。首先对这方面的进展作一个简要综述，通过具体事例重点展示其在铸锭铸态组织和宏观偏析形成过程动态数值仿真的应用前景，指出目前存在的某些局限性。

关键词：凝固； 铸锭； 宏观偏析；铸态组织； 数值仿真

DOI:10.7502/j.issn.1674-3962.2015.09.02