AZ31镁合金方管挤压成型的数值模拟

孙颖迪，李光振，陈秋荣

(中国科学院上海微系统与信息技术研究所轻合金技术工程中心，上海 200050)



AZ31镁合金方管挤压成型的数值模拟

孙颖迪，李光振，陈秋荣

(中国科学院上海微系统与信息技术研究所轻合金技术工程中心，上海 200050)

摘要：基于AZ31镁合金热压缩真应力-真应变曲线，计算得到了流变应力方程，分析了合金压缩变形后的显微组织，并用HyperXtrude有限元分析软件对AZ31镁合金方管挤压成型进行了数值模拟，最后进行了试验验证。结果表明：AZ31镁合金的流变应力随变形温度的升高而减小，并在350 ℃以上较快达到稳态，易于加工成型；热压缩变形后合金中的孪晶组织随温度的升高有所减少，且晶粒不断长大，在高应变速率时由于动态再结晶不充分，晶界附近形成类似“项链”状的细小晶粒组织；有限元模拟分析发现方管角部金属流速低于中心位置，在HyperStudy中经工作带优化后流速分布均匀，采用优化设计的模具挤压生产出了合格的AZ31镁合金型材。

关键词：AZ31镁合金；热压缩；挤压成型；数值模拟

0引言

图1　AZ31镁合金在不同温度和应变速率下的真应力-真应变曲线Fig.1　True stress-turestrain curves of AZ31 magnesium alloys at different deformation temperatures and strain rates

镁合金作为密度最小的金属结构材料，具有比强度高以及散热性好等优点，被誉为“21世纪最具开发和应用潜力的绿色工程材料”，在航空航天、汽车、通讯与电子工业领域有着广阔的应用前景[1-2]。目前，镁合金的成型多以模铸、压铸以及半固态成型为主，但镁与其它元素在结晶时分布的不均匀性导致镁合金铸件常伴有成分偏析以及力学性能偏低等缺陷，限制了其应用进程。在铸造成型后进行塑性变形能很好地弥补镁合金的上述缺陷，大幅度改善其强度与塑性。其中，挤压成型以其型材的高精度、高性能及低的表面粗糙度等优势被广泛接受；空心型材则以其显著的低耗材性，同时满足了产品轻量化的结构使用要求，相比实心型材具有更明显的技术经济价值。然而，空心镁型材分流模具固有的结构复杂性使试模周期普遍偏长，试模成本较高[3-4]。

数值模拟是依靠计算机并结合有限元等各类算法建立数学模型，模拟解决工程或物理问题的一种方法，它大大减少了昂贵的现场试模成本，提高了工模具设计效率，在材料加工领域的应用日益广阔[5-6]。易杰等[7]用Flow-3D对ADC12铝合金门内板挤压铸造过程进行了有限元分析，对模具温度、浇注温度以及压机速度等工艺参数进行了优化，生产出良好的制件；王冠等[8]根据6063铝合金型材的尺寸超差有限元分析，通过添加阻流块的方式改善了金属流速，优化了模具结构；王春燕等[9]通过Ansys有限元软件对TB8钛合金半球的拉深成形和超塑性气胀成形过程进行模拟，获得了最佳的半球成形工艺。然而，纵观文献报道，目前关于AZ31镁合金挤压成型与模具优化的研究仍相对较少，基于ALE算法的有限元软件HyperXtrude(HX)的应用也较为匮乏。为此，作者基于对AZ31镁合金热压缩行为的分析，构建了流变应力方程，并以典型的镁合金方管为研究对象，利用HX软件对方管的挤出成型过程进行模拟，并通过引入能够表现型材出口处截面速度均匀性的目标函数与HyperStudy模块优化挤压模具工作带尺寸，为后期复杂型材的模具设计提供重要依据。

1试验方法与结果

1.1　试验方法

试验材料为AZ31镁合金，制成φ10 mm×15 mm的圆棒试样，采用Gleeble3500型热力模拟试验机在不同的温度(250，300，350，400，450，500 ℃)下进行应变速率为0.001，0.01，0.1，1，10 s-1的单向热压缩变形试验并记录试样的真应力-真应变曲线。高温压缩后的试样水冷后用300#～1000#砂纸逐级打磨后抛光，并用草酸醋酸溶液腐蚀，用Leica DM2500型光学显微镜观察其显微组织。

1.2　应力-应变曲线与显微组织

由图1可以看到，试样在压缩变形过程中，其流变应力随变形温度的升高而减小。这是由于温度升高，会开启更多的滑移系，使试样的塑性变形能力增强，变形抗力减小，且温度升高后试样内部的动态回复与动态再结晶更容易，故应力的峰值随温度升高而降低。流变应力的变化与试样在变形过程中发生加工硬化与动态再结晶密切相关，变形初始阶段，位错密度增加，加工硬化严重，动态再结晶仅部分发生，因此流变应力迅速上升；当应力达到峰值后，加工硬化与动态再结晶达到平衡，随压缩变形而进行的动态再结晶将更为充分，软化作用加强，应力减至稳态。在350 ℃以上时流变应力能较快达到稳态，此时AZ31镁合金能够稳定变形，且变形抗力较低，材料易于加工成形。

由图2可以发现，在变形温度为250～350 ℃时，试样晶粒内存在大量孪晶组织，如图中箭头所示。随着温度的升高，孪晶组织有所减少，这是由于温度升高后镁合金材料的塑性提高，加工硬化效应减小所致[11]。当温度升至400～500 ℃时，晶粒内的孪晶组织基本消失；同时，随着温度的升高，晶粒尺寸逐渐增大，这是由于温度升高使晶界扩散与晶界迁移能力增强，晶粒容易长大而粗化[12]。

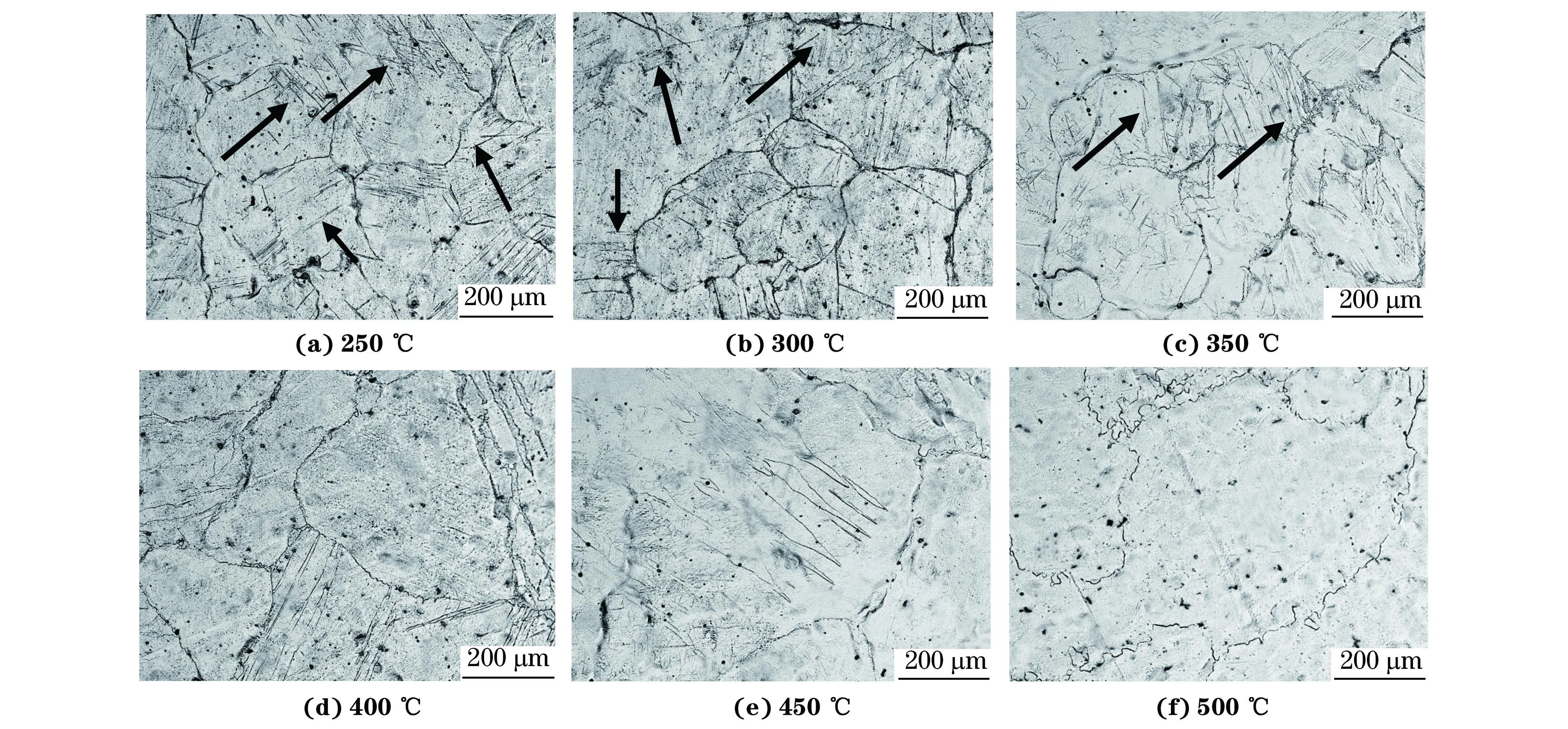
图2　应变速率为0.1 s-1时不同温度压缩变形后试样的显微组织Fig.2　Microstructures of the specimens after compression deformation at different temperatures and strain rate of 0.1 s-1

图3　400 ℃时不同应变速率下压缩变形后试样的显微组织Fig.3　Microstructures of the specimens after compression deformation at the temperature of 400 ℃ and different strain rates

由图3可以看到，在400 ℃下，应变速率对晶粒尺寸有明显影响。由于AZ31镁合金在高温下晶界强度较低，变形首先从晶界处开始，因此会在晶界处产生较大位错密度，从而促使晶界及其附近区域首先发生动态再结晶[13]。当应变速率较低时，镁合金的动态再结晶过程进行较充分，晶粒有足够的时间长大，因此在晶界处观察不到细小晶粒的存在；当应变速率较大时，由于变形时间短，动态再结晶过程进行并不充分，晶粒来不及长大，所以晶界处会出现许多细小的晶粒[14]，如图3(e)所示，当应变速率达到10 s-1时，可以看到在晶界附近形成类似“项链”状组织。

1.3　流变应力方程

金属热加工过程的流变应力方程通常可以表示为[15]：

(1)

由于典型的金属热加工流变曲线中会出现应力峰值和其后稳定的流变阶段，此时状态参量S是应变速率与变形温度的函数，故流变应力方程可表示为：

(2)

Tegart和Sellars基于式(1)提出了双曲线正弦修正的Arrhenius修正关系，能够合理描述合金在整个变形温度与应变速率范围内的塑性变形行为，即：

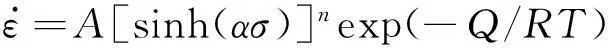
(3)

式中：Q为变形激活能；n为应力指数；R为气体常数，为8.314 J·mol-1·K-1；A和α为与材料有关的常数。

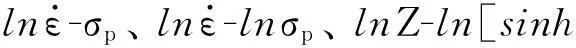
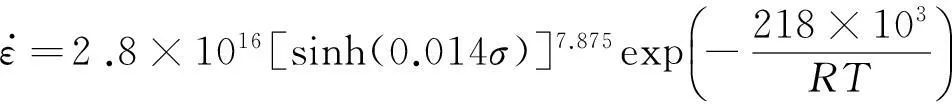
(4)

2有限元建模与模具结构

2.1　方管挤压模具设计

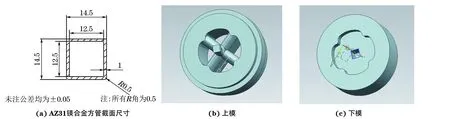
图4　AZ31镁合金方管截面尺寸与模具三维示意Fig.4　Cross-section dimension of AZ31 magnesium alloy square tube(a) and three-dimension graph of the extrusion die:(b) plunger die and (b) bottom die

图5　有限元分析模型Fig.5　Mesh of the finite element model

图4(a)为AZ31镁合金方管截面形状与主要尺寸。由图4(a)可以看到，该型材壁厚仅1 mm，横截面积为54 mm2。图4(b)和(c)分别为上模与下模的三维结构，上模外形尺寸为φ149 mm×66.5 mm，采用四扇形分流孔，下模为φ149 mm×57 mm，焊合室高度为14 mm，分流比为40。为强化金属流动与焊合，将分流桥截面设计为水滴形。2.2有限元模型

将Unigraphics软件中建立的模具三维模型导入到HyperXtrude有限元分析软件，根据方管对称性取1/8模型进行计算，几何清理后划分网格，如图5所示。模型分为坯料、分流孔、焊合室、工作带与出口型材五个部分，其中，工作带与出口型材部分网格采用三棱柱单元，其他各部分网格采用四面体单元，网格最小尺寸约为0.18 mm，网格总量约60 000个。由于坯料部分变形较小，网格单元尺寸从工作带到坯料逐渐增大，既不影响计算精度，又可节省计算时间，提高效率。另外，模拟过程用式(3)流变应力本构方程作为AZ31镁合金的材料变形模型。

在挤压过程中，坯料在挤压筒内壁、分流孔及焊合室模面附近变形剧烈，摩擦条件设为粘着摩擦；在模具工作带部分摩擦条件缓和，设为库仑摩擦，摩擦因数取0.3。模拟中所采用的具体工艺参数见表1。该试验前期模型分析与数值模拟在工作站上求解完成。

表1　挤压工艺参数设置

2.3　方管挤压模拟与模具工作带优化

2.3.1方管挤压模拟结果

对方管挤压模型进行仿真计算，能够得到合金变形过程中温度场、应力应变场以及金属流速场的分布情况。由图6可以看出，挤压温度沿挤压方向逐渐升高。初始阶段，由于接触传热，坯料温度与挤压筒接近，当坯料流入分流孔后由于挤压变形其温度达到470 ℃以上，进入焊合室后温度达到490 ℃，且焊合室内靠近工作带部位的温度明显高于边缘部位的，当坯料进入工作带后温度达到最高，约为500 ℃。

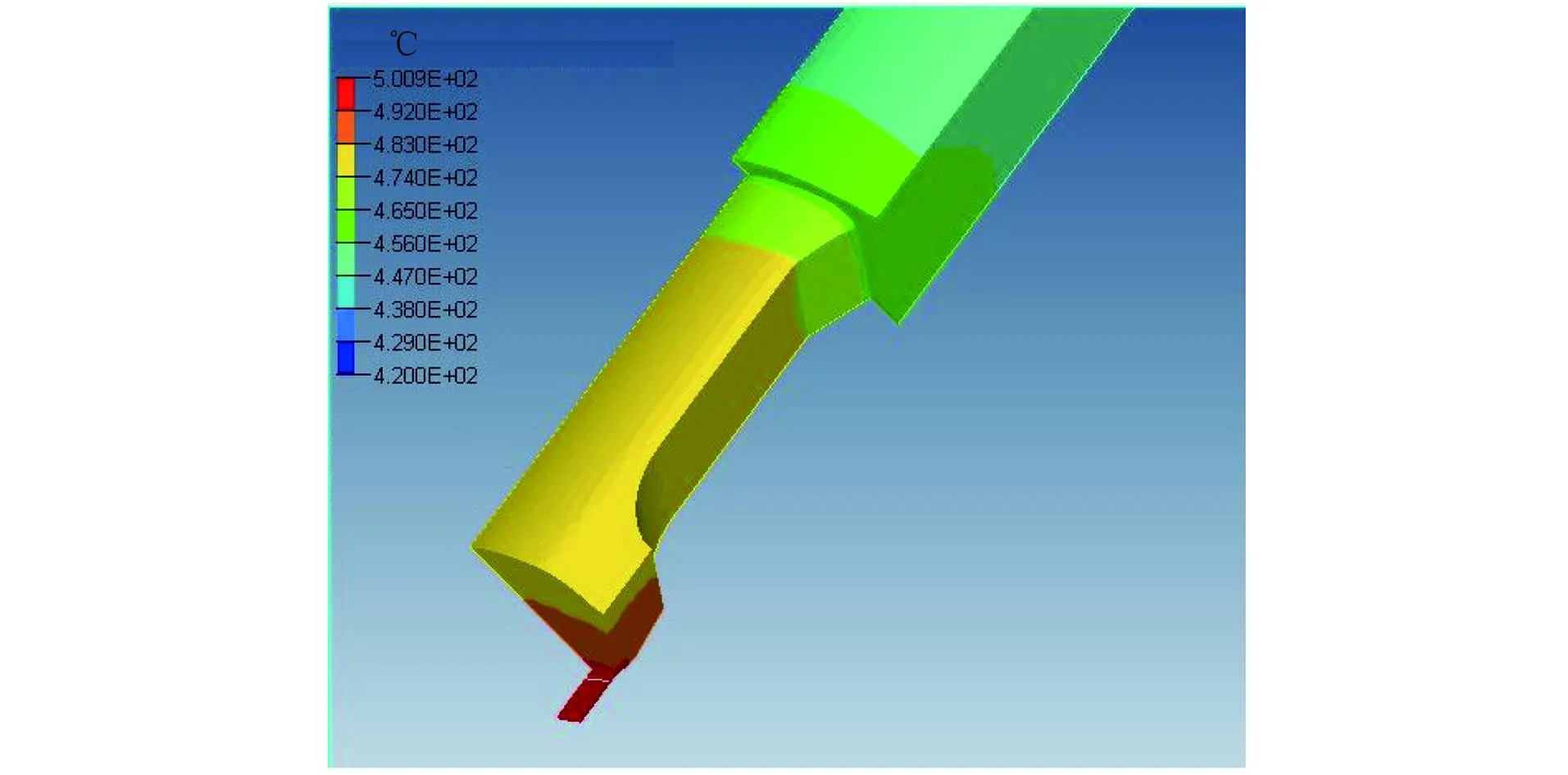
图6　方管的挤压温度分布云图Fig.6　Temperature distribution of the square tube duringextrusion process

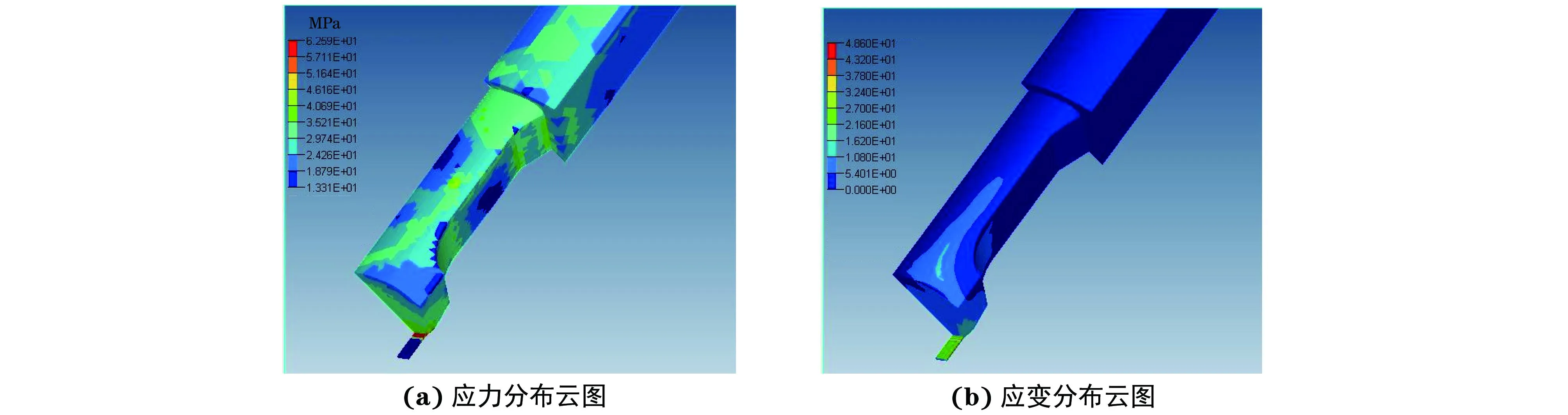
图7　方管的挤压应力与应变分布云图Fig.7　Stress (a) and strain (b) distribution of the square tube during extrusion process

从图7可以看出，坯料在挤压筒内所受压力较小，发生的应变也较小。进入分流孔后，坯料所受的应力有所增大，在焊合室内所受的应力则明显高于其他部位的，并在工作带部位达到最大，约62.59 MPa，说明此处变形剧烈，相应的应变值达到最大，约48.6。由图8可以看出，按表1设置的工艺参数挤压过程中，金属流速较均匀，角部与心部金属存在少量流速差。方管角部的金属流速要低于心部的，这是由于角部距离挤压轴较远所致，可通过工作带优化模块对工作带尺寸进行优化以获得更合理的模具结构。

图8　方管的挤压工作带处金属流速分布云图Fig.8　Velocity distribution in the bearing part of the square tubeduring extrusion process

2.3.2方管挤压模具工作带优化

在HyperStudy模块中，根据型材出口截面金属流速的不均匀性将截取的型材出口截面分为两区，如图9所示，截面金属流速分别为v1和v2。目标函数如式(5)所示，目标值设为1 000。

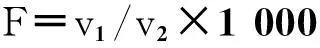
(5)

图9　对应工艺参数设置的截面分区与模具工作带金属流速分布云图Fig.9　The partition of cross-section and velocity distributionof die bearing under the corresponding parameters

设置6条工作带控制线L0～L5，位置如图9所示。其中，贴近型芯位置设计两条控制线L0和L1，且L0=L1。模具工作带初始长度设为2 mm。优化过程中当目标值接近1 000时，可认为截面流速比较均匀，达到了优化目标。迭代结果如表2所示，经过7次迭代，目标值达到1 000。

图10(a)~(d)分别为第1次、第2次、第6次与第7次迭代计算的型材出口速度分布情况。可以看出，当工作带取初始值2 mm时，型材出口截面速度分布在484.87～484.98 mm·s-1范围内，速度分布均方差达到0.21 mm·s-1，金属流速分布略有不均；经7次迭代计算后达到最优化水平，优化后出口截面速度差降为0.01 mm·s-1，速度分布均方差减小为0.008 mm·s-1，工作带各部位的长度更加合理。

表2　HyperStudy迭代过程

3方管挤压试验验证

用第7次迭代计算优化的工作带尺寸作为最终模具工作部分尺寸加工模具，并在630T型卧式挤压机上完成型材挤出，图11为实际型材。型材表面质量较好，硬度达到67 HV，抗拉强度为279 MPa，伸长率为14%，均质检合格，说明模拟结果能够为实际生产提供可靠参考。

图11　实际挤压型材的外形Fig.11　The shape of practical extruded profile

4结论

(1) 通过热模拟试验得到AZ31镁合金的真应力-真应变曲线，根据Arrhenius修正关系计算获得其流变应力方程；在热变形过程中，其流变应力随变形温度的升高而减小，在350 ℃以上能够较快达到稳态，易于加工成形。

(2) 热压缩变形后，AZ31镁合金中孪晶组织随变形温度的升高而减少，晶粒尺寸不断增大；在高应变速率时由于动态再结晶不充分，在晶界附近形成类似“项链”状的细小晶粒组织。

(3) 对镁合金方管挤压过程进行数值模拟发现，方管角部金属流速低于中心位置;经HyperStudy模块的工作带优化设计后，金属流速分布趋于均匀，出口截面速度差降为0.01 mm·s-1，速度分布均方差减小为0.008 mm·s-1。

(4) 采用优化设计的模具生产出了合格的镁合金型材，表明基于HyperXtrude有限元模拟与材料流变应力方程能够为AZ31镁合金型材生产提供可靠参考。

参考文献:

[1]罗昊. AZ31镁合金挤压板材的力学性能和耐腐蚀性能[J]. 机械工程材料, 2013, 37(10): 60-63.

[2]郜瑞, 温彤, 季筱玮, 等. 工艺参数对AZ31镁合金板拉深成形性能的影响[J]. 机械工程材料, 2013, 37(3): 87-89.

[3]CHEN H, ZHAO G Q, ZHANG C S,et al.Numerical simulation of extrusion process and die structure optimization for a complex aluminum multicavity wallboard of high-speed train[J]. Materials and Manufacturing Processes, 2011, 26(12): 1530-1538.

[4]ZHANG C S, ZHAO G Q, CHEN Z R,et al.Effect of extrusion stem speed on extrusion process for a hollow aluminum profile[J]. Materials Science and Engineering: B, 2012, 177(19):1691-1697.

[5]GUAN Y J, ZHANG C S, ZHAO G Q, et al. Design of a multihole porthole die for aluminum tube extrusion[J]. Materials and Manufacturing Processes, 2012, 27(2): 147-153.

[6]ZHANG C S, ZHAO G Q, CHEN H,et al. Numerical simulation and metal flow analysis of hot extrusion process for a complex hollow aluminum profile[J]. The International Journal of Advanced Manufacturing Technology,2012,60(1):101-110.

[7]易杰, 朱必武, 李落星. 铝合金车门内板挤压铸造工艺优化的有限元模拟[J]. 机械工程材料, 2014, 38(5): 89-94.

[8]王冠, 何芯, 李落星, 等. 6063铝合金挤压型材尺寸超差分析及模具优化设计[J]. 机械工程材料, 2013, 37(7): 85-89.

[9]王春艳, 谢兰生, 陈国亮. 超薄TB8钛合金半球成形工艺的有限元模拟[J]. 机械工程材料, 2012, 36(11): 102-105.

[10]李光振, 孙颖迪, 陈秋荣, 等. 基于HyperXtrude的镁型材挤压数值模拟与模具优化研究[J]. 热加工工艺, 2014, 43(13): 118-120.

[11]黄光杰, 赵国丹. AZ31镁合金热变形规律的研究[J]. 重庆工学院学报, 2006, 20(2): 60-65.

[12]孙述利, 张敏刚，周俊琪. AZ31镁合金热压缩过程中的变形行为[J]. 机械工程材料, 2010, 34(8): 88-91.

[13]孙朝阳, 栾京东. AZ31镁合金热变形流动应力预测模型[J]. 金属学报, 2012, 48(7): 853-861.

[14]余琨, 史褆, 王日初. AZ31镁合金变形行为的热力模拟[J]. 中南大学学报, 2008, 39(2): 216-221.

[15]JONAS J J, SELLARS C M, TEGART W J. Strength and structure under hot-working conditions[J]. International Materials Reviews, 1969, 14(1): 1-24.

[16]王火生,傅高升,陈永禄,等.铝锰镁合金热压缩变形的流变应力曲线与本构方程[J].机械工程材料,2014,38(5):95-98.

Numerical Simulation of Square Tube Extrusion for AZ31 Magnesium Alloys

SUN Ying-di, LI Guang-zhen, CHEN Qiu-rong

(Light Alloy Engineering Center, Shanghai Institute of Micro-system and Information Technology,

Chinese Academic of Science, Shanghai 200050， China)

Abstract:On the basis of true flow stress-true strain curves of AZ31 magnesium alloys obtained from hot compression process, the corresponding flow stress equation was presented and the microstructure of the compressed alloy was analyzed. The square tube extrusion process for AZ31 magnesium alloy was simulated by using the HyperXtrude software. The results show that the flow stress decreased with the increasing temperature and could reach the steady state quickly above 350 ℃, which is suitable for processing forming. The twins in hot compression specimens reduced with the temperature increasing, moreover the grains were growing up. With the high strain rate, the fine grains similar to “necklace” appeared on the grain boundaries due to the insufficiency of dynamic recrystallization. The finite element simulation results show that the metal velocity in the corner of the square tube was lower than that in the center, but could distribute well as the optimization of the bearing part in the HyperStudy. The die designed on the optimized die bearing model proved to be capable of producing the qualified products in practice.

Key words:AZ31 magnesium alloys; hot compression; extrusion molding; numerical simulation

中图分类号：TG379

文献标志码：A

文章编号：1000-3738(2015)10-0084-06

作者简介：孙颖迪(1983-)，女，山东青岛人，助理研究员，博士。

基金项目：嘉兴市重大科技专项项目(2010AZ2001)

收稿日期:2014-09-04；

修订日期:2015-07-23

DOI:10.11973/jxgccl201510019 10.11973/jxgccl201510020