运输问题最小元素法的一个原则

史书慧

(沈阳工程学院 基础部，辽宁 沈阳 110036)



运输问题最小元素法的一个原则

史书慧

(沈阳工程学院 基础部，辽宁 沈阳 110036)

表上作业法是简单有效的求解运输问题的算法，而初始方案的确定对表上作业法尤为重要。对此提出了使用最小元素法的一个原则，利用该原则可以避免可能存在的多余计算过程，从而减少调整次数。利用实际算例验证了所提出方法的正确性和有效性，并得到最小元素法求初始解的两个结论。

运输问题;初始方案;最小元素法

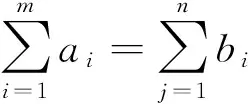
此外，产销不平衡的运输问题也可以转化为产销平衡问题[1-2]。关于运输问题，现在广为使用的方法是表上作业法[3]，对于表上作业法的研究和改进已经引起了众多学者的兴趣[4-12]。用表上作业法求解运输问题时，需要首先给出一个初始方案，这个初始方案的选取很大程度上决定了后续检验、调整等循环步骤的次数，即而决定了得到最优解的时间[4]。因此如何确定初始方案才能尽可能地减少迭代次数正是需要探讨的问题。

1 最小元素法使用原则

常见的初始方案求法有西北角法(或左上角法)、最小元素法和Vogel法。一般地，Vogel法求得的初始基可行解质量最好，最小元素法次之，左上角法最差[5]。最小元素法简便易行，但求得的初始基可行解与最优解的接近程度不及Vogel法。Vogel法得到的初始方案最接近最优解，但每次均需计算各行各列最小元素与次小元素之差，某种程度上增加了计算工作量。经典最小元素法是确定单位运价表中的最小元素，建立供销关系(即填上尽可能大的数)，当同时存在两个或两个以上的相同最小元素时，任选其中一个最小元素，这样任意选择可能使迭代次数增加，计算繁琐。综合分析后，给出了这样一个处理原则：若相同最小元素存在于一列(行)上，则需要分别计算其所在行(列)中与次小元素的差额，并确定最大的差额，再按最大差额所在行(列)的最小元素建立供销关系，划掉已满足要求的行或列；若该最小元素所在行或列的产量和销量相等时，则需要同时划掉对应的一行或一列，这时在对应划掉的一行或一列的一个空格处补0。对未划去的行或列重复上述步骤，直到得到一个初始解。

2 实例分析

已知某运输问题的产销地供应量与单位运价，如表1所示，试用表上作业法求其最优解。

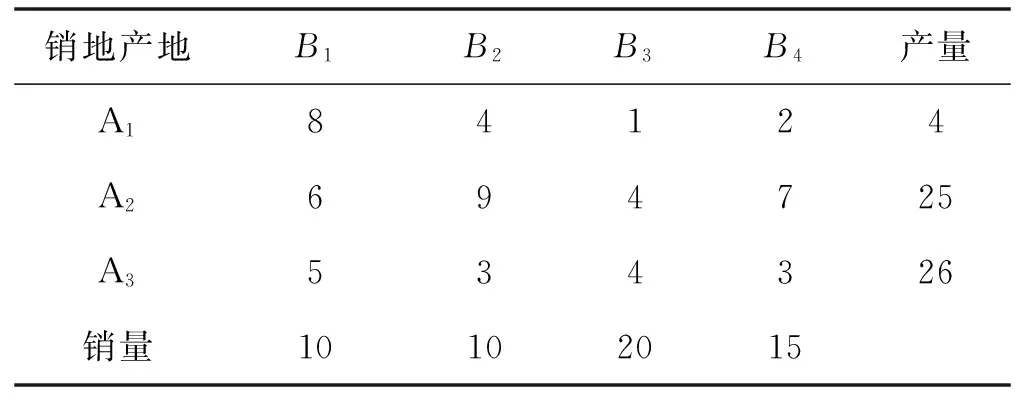
表1 某运输问题的产销地供应量与单位运价

方法一：用最小元素法求初始可行解可按下述步骤进行：

Step 1：按照最小元素1进行调运，在初始方案表2中(A1，B3)处填写4，划去A1行；

Step 2：未划去的元素中最小元素为3，分别在(A3，B2)和(A3，B4)处，这时应用提出的原则，分别计算第2列和第4列中最小元素与次小元素的差额，按最大差额6所在的第2列的最小元素3调运，在表2中(A3，B2)处填写10，划去B2列；

Step 3：未划去的元素中最小元素为3，在(A3，B4)处，则A3给B4供应，在表2中(A3，B4)处填15，划去B4列；

Step 4：未划去的元素中最小元素为4，分别在(A2，B3)和(A3，B3)处，这时应用提出的原则，分别计算第2行和第3行中最小元素与次小元素的差额，按最大差额2所在的第2行的最小元素4调运，在表2中(A2，B3)处填16，划去B3列；

Step 5：未划去的元素中最小元素为5，在(A3，B1)处，则A3给B1供应，在表2中(A3，B1)处填1，划去A3行；

Step 6：未划去的元素中最小元素为6，在(A2，B1)处，则A2给B1供应，在表2中(A2，B1)处填9，得到初始可行解，相应的总运费 ；

Step 7：用位势法检验，所得结果如表3所示；

Step 8：表3中括号里的数即为检验数，因为所有的检验数都大于或等于零，所以表2中给出的初始调运方案即为最优方案，最小运费为202。

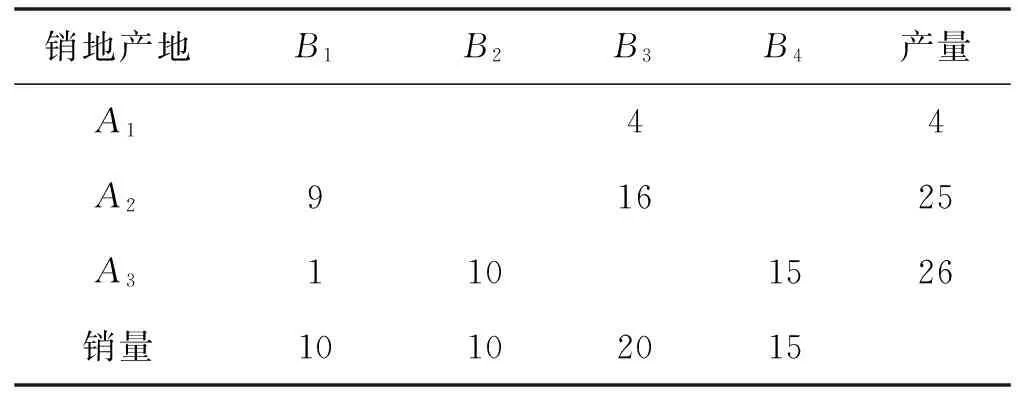
表2 按照最小元素1进行调运的初始方案

表3 位势法检验方法一的结果

如果在出现两个或两个以上相同最小元素时，不采用所提出的准则进行调运，即按照传统的最小元素法(任选其一)求解，则会出现以下几种结果。

方法二：如果选相同最小元素3时，先选(A3，B2)，再选(A3，B4)；选相同最小元素4时，先选(A3，B3)，再选(A2，B3)，所得到的初始方案如表4所示，总运费z=4×1+10×6+15×4+10×3+1×4+15×3=203。

表4 按方法二所得到的初始方案

表5 位势法检验方法二的结果

用闭回路法调整，得新的调运方案，与表2中的方案相同，则再由方法一得到最优方案。

方法三：如果选相同最小元素3时，先选(A3，B4)，再选(A3，B2)；选相同最小元素4时，先选(A3，B3)，再选(A2，B3)，则得到的初始方案与表4中的方案相同，再根据方法二能得到最优方案。

由上述3种方法可知，当选多个相同最小元素之一时，得到的目标函数值可能不一样，若按最小差额所在行(或列)的最小元素调运，则可能使调整次数增加。

方法四：如果选相同最小元素3时，先选(A3，B4)，再选(A3，B2)；选相同最小元素4时，先选(A2，B3)，则选不到(A3，B3)，得到初始方案与表2中的方案相同，再根据方法一能得到最优方案。

对比方法一和方法四(或方法二、方法三)可知，若有多个相同最小元素时，无论先选哪一个，其他的都能被选到时，则得到的初始方案一样。

3 结 论

最小元素法是求运输问题初始可行解的一个较为简便的方法，当同时存在多个相同最小元素时，任选其中一个可能使实际调整次数增加。 如果在遵循最小元素法的基本原理基础上,按所提出的使用原则进行处理,会使迭代次数明显减少,从而简化计算工作量。

[1]运筹学教材编写组.运筹学[M].北京：清华大学出版社，2005.

[2]胡运权.运筹学基础及应用[M].第5版.北京：高等教育出版社，2014.

[3]韩伟一,张庆普.运输问题表上作业法的一点注记[J].运筹与管理，2009，18(4)：7-9.

[4]刘大为，张方华.运输问题表上作业法的改进[J].科技资讯，2008(12):248-249.

[5]刘晓岚.表上作业法求解运输问题的思考[J].山东省农业管理干部学院学报,2009，23(6)：155-156.

[6]谢凡荣.产销平衡运输问题的表上作业法解法的一个注记[J].运筹与管理，2005，14(4)：44-46.

[7]郭秀英.论运输问题表上作业法[M].科技与管理，2007(3)：33-35.

[8]耿 雪，段川会.改进的最小元素法及其在物资配送问题中的应用[J].物流工程与管理，2010，32(6)： 108-111.

[9]王广民，马林茂，李兰兰.运筹学中运输问题求解算法及其扩展研究[J].长江大学学报，2011，8(10)： 1-6.

[10]张晓瑾，刘海生.运输问题的表上作业法中初始方案的优化[J].华北科技学院学报，2014，11(6)： 73-79.

[11]段春香.论表上作业法与单纯形法的一致性[J].怀化学院学报，2013，32(11)： 78-81.

[12]陈海伟，陶庆玲.表上作业法在有转运的物资运输问题中的应用[J].河南教育学院学报，2012，21(2)： 20-23.

(责任编辑 张 凯 校对 佟金锴)

A Principle on Minimum Element Method of Transportation Problem

SHI Shu-hui

(Department of Preparatory Course,Shenyang Institute of Engineering,Shenyang 110136,Liaoning Province)

The table-working method is a simple and efficient algorithm for solving transportation problems.The determination of the initial scheme for table-working method is particularly important.In this paper,a principle of minimum element method is presented,which can avoid the possibly existing redundant calculation and reduce the number of adjustments.An example is given to verify the correctness and validity of the proposed method,and two conclusions of the minimum element method are derived.

transportation problem；initial scheme；minimum element method

2015-01-13

史书慧(1983-)，女，辽宁铁岭人，讲师，博士，主要从事运筹学与控制论方面的研究。

10.13888/j.cnki.jsie(ns).2015.03.022

O122

A

1673-1603(2015)03-0286-03