dbN小波变换在超短期风功率预测中的应用研究
2015-02-24钟宏宇田明辉
钟宏宇,高 阳,钟 超,田明辉,武 良
(沈阳工程学院 a.研究生院; b.电力学院,辽宁 沈阳 110136)
dbN小波变换在超短期风功率预测中的应用研究
钟宏宇a,高 阳b,钟 超a,田明辉a,武 良a
(沈阳工程学院 a.研究生院; b.电力学院,辽宁 沈阳 110136)
为了降低风速序列的非平稳性,研究了基于dbN小波变换及单位置NWP的超短期风功率预测模型。采用小波多分辨率分析法对原始风速时间序列进行分解,滤除高频分量,滤出低频分量,低频分量能够对风功率预测起到决定作用。然后,利用线性校正数学模型对超短期风速时间序列进行预测,并采用巴特沃兹低通滤波器对校正后的风速进行滤波。实验结果证明,该方法可有效地提高超短期风功率的预测精度。
小波变换;超短期;滤波;风功率预测
风能作为一种可再生、洁净能源,近几年来在全球范围内得到了举世瞩目的发展。由于风能具有波动性、间歇性、低能量密度、不可控性等特点,大规模风电并网对电力系统的安全稳定运行带来了很大的困难。因此,风电场超短期风功率预测受到了越来越多国内外学者的关注。准确的超短期风功率预测,可以减少旋转备用容量,减小风电系统成本,并且为电网合理调度提供可靠的依据。
风功率预测实质上就是对风速的预测,可由公式P=CpAρv3/2决定,式中:P为风轮输出功率;Cp为风轮的功率系数;ρ为空气密度;A为风轮扫掠面积;v为风速。从公式中可知,风电机组输出功率P与风速v的三次方成正比,风速的微小变化反应到风电机组的输出功率上将会有很大的变化,所以影响输出功率的主要因素是风速。其特性曲线如图1所示。风速主要体现为两种特性[1]:
1)由于风能的能量密度较低,温差、阴晴、雨水等均会引起风速的变化,因此风速变化存在很大的波动性,表现为非平稳的随机信号。
2)由于风速的变化跟光的照射强弱有密切关系,所以在一天中风能的强弱在某种程度上又呈现周期性。
小波函数恰好可以用来分析非线性、非平稳信号的局部特性[2],利用小波函数对原始风速时间序列进行分解,滤除其高频分量,保留其平稳的低频分量,该低频分量蕴含着空气流体中的主要能量,对风功率预测精度具有决定性作用。
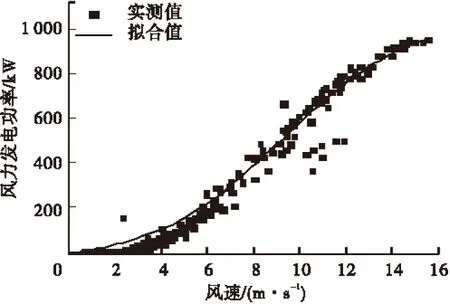
图1 风电机组输出特性曲线
1 小波变换
1.1 小波变换定义
小波变换是一种信号的时间-频率局域分析方法,它通过伸缩和平移等运算功能对信号进行多尺度细化分析(Multiscale Analysis),而且在时域和频域均具有表征信号局部特性的能力。小波变换在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,很适合于探测正常信号中夹带的瞬态反常现象并展示其成分,有分析信号的显微镜的美誉[3]。小波变换包括连续小波变换和离散小波变换。
1.2 多分辨分析
将信号x(t)正交投影到空间Vj和Wj,能对应得到分辨力j下x(t)的离散逼近信号cj(t)和离散细节信号dj(t)[4]。令j由零逐级增大,便可得到信号分解的逐级实现,每一级分解的结果是将上次分解得到的低频信号再分解成低频和高频两部分,而高频信号可忽略,如图2和图3所示。

图2 多分辨率分析空间解析
1.3 小波函数的选定
常用的小波函数[5]大致包括Haar小波、墨西哥帽小波、Morlet小波、Daubechies小波等。
为了能够有效地使用小波分析进行超短期风功率预测,首先必须选择出一个合适的小波函数。由于小波函数具有多样性,同一个工程问题应用不同的小波分析会有不同的结果。在进行超短期风功率预测时,时间序列具有多重周期性,因此选取dbN小波作为超短期风功率预测的理论函数。该函数具有以下的特性。
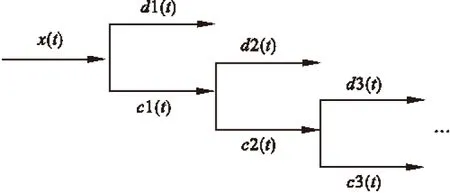
图3 多分辨分析的分解过程
1) 良好的紧支撑性
设Ψ(t)为某一小波函数,若该函数在区间[a,b]外恒为零,则称该函数在这个区间上紧支撑,具有该性质的小波称为紧支撑小波。
2) 消失矩R值愈高愈好
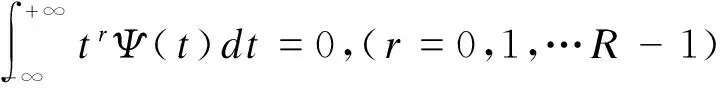
3) 良好的正则性
如果函数在区间[a,b]内k-1阶连续,但k阶导数不连续,则称该函数在这个区间k-1阶光滑。正则性在数学建模上表现为小波基的可微性或光滑性,对于大多数正交基,正则性越高则消失矩越高。
众多实践表明dbN小波可以用来很好的分析时间序列问题。关于N选择标准如下:
①小波函数Ψ(t)和尺度函数Φ(t)的有效支撑长度为2N-1。良好的紧支撑性要求N越小越好;②正则性随着N的增加而增加;③消失矩为N,消失矩N越高越好。
由此可见,紧支撑性、正则性和消失矩彼此间相互约束,从而使得N值不会太小也不会无限大。采用皮尔逊积矩相关系数[6]作为选择dbN小波的标准,皮尔逊积矩相关系数用R表示,它的基本公式为
(1)
其中,E是数学期望,cov表示协方差。该系数R的值域为[-1,1]。其性质如下:
1)当R>0时,表示X和Y正相关,R<0时,表示X和Y负相关。
2)当|R|=l时,表示X和Y为完全线性相关,即为线性函数关系。
3)当R=0时,表示X和Y之间无线性相关关系。
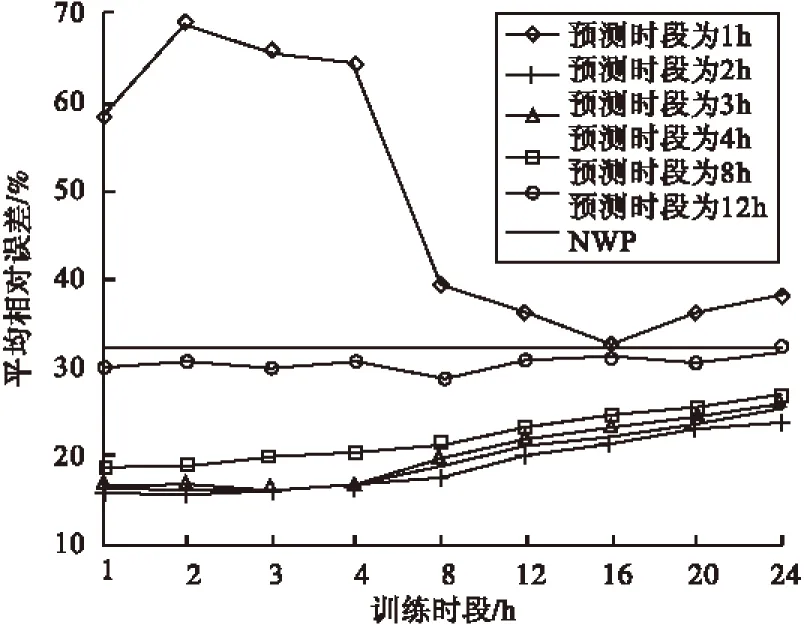
4)当0<|R| 5)一般可按三个等级对R的绝对值进行划分:|R|<0.4为低度线性相关;0.4≤|R|<0.7为显著性相关;0.7≤|R|<1为高度线性相关。 由于NWP数据是针对高空大气环流动力学模型演化得到的,因此对于风机轮毂高度的风速预测会有一定的系统偏差: (2) 其中,es为系统偏差,vreal为实测风速值,vNWP为预测风速值,N为预测样本长度。 该系统偏差主要是由于地形、地表粗糙度、风向以及风机尾流效应等影响所致。假设在短期时间尺度内系统偏差es保持不变: es_train≈es_test (3) 其中,es_train为训练时段的系统偏差,es_test为预测时段的系统偏差。可利用测风塔实测风速对未来NWP风速进行校正: [vreal(k),…,vreal(k-4T1+1)]= f[vNWP(k),…,vNWP(k-4T1+1)] (4) [Vrevise(k+1),…,vrevise(k=4T2)]= f[vNWP(k+1),…,vNWP(k+4T2)] (5) 其中,vrevise为校正后的风速值,T1为训练时段,T2为预测时段。训练时段是指预测起始点之前的T1时段,其数据用于校正模型的训练样本。 对每个样本求取es_train和es_test,可得到系统偏差序 列:Xs_train=[es_train(1),es_train(2),…,es_train(K)],Xs_test=[es_test(1),es_test(2),…,es_test(K)],K为样本个数。当每个样本系统偏差均满足式(3)时,可以认为: Xs_train≈Xs_test (6) 即可利用式(4)、(5),对每个样本T2时段的NWP风速进行校正。该方法的核心是系统偏差在短期时间尺度内保持不变,因此要求Xs_train和Xs_test具有较强的相似度,可以利用皮尔逊积矩相关系数作为衡量2个时间序列相似度的指标。 由于NWP风速变化平缓,导致由NWP风速时间序列建模的系数矩阵中,各行近似线性相关,出现方程病态,使得求出的解非常大,导致校正风速出现小于0的情况。所以有必要对校正后的风速进行滤波处理,消除病态方程的影响。 采用巴特沃兹滤波器对校正后的风速进行滤波,参数设计为:通带边界频率0.1π,阻带边界频率0.3π,通带纹波3 dB,阻带衰减19 dB,离散化方法选用双线性变换法。幅频特性曲线如图4所示。 图4 巴特沃兹滤波器幅频特性曲线 采用该巴特沃兹滤波器对校正后的风速进行滤波的前后对比如图5和图6。可见加入巴特沃兹滤波器后可修正失真风速并提高超短期风功率预测精度。 图5 对比前数据 图6 对比后数据 4.1 实测数据修正 在小波分解前,为了防止极端风速以及病态数据对分析的影响,需要对实测风速进行修正。选取国内某风电场单位置(以下简称Y风场)2014年的实测风速时间序列,得到风速威布尔分布曲线,如图7所示。 将概率分布为5%和95%的风速分别记为vmin和vmax,用式(7)对训练时段的实测风速进行修正: v(i)=vmax,ifv(i)>vmax (7) 4.2 dbN选取 用db2、db3、db4、db5对Y风电场2014年3月份的实测风速和NWP风速进行3~6层的分解,并计算二者低频分量的皮尔逊相关系数,如表1所示。 图7 Y风场2014年风速分布曲线 M层dbN 3456db20.700.810.900.97db30.660.800.910.81db40.640.780.750.93db50.670.810.900.97 当M小于等于4时,皮尔逊相关系数R均小于0.9,说明实测风速低频部分和NWP风速低频部分线性相关性较差;当M=6时,尽管相关性变高,但风速低频部分变陡,平滑性变差;当M=5时,db3小波的R最大,所以选取db3小波,分解层数M选为5。db3小波(M=5)的各尺度波形如图8所示。 采用紧支撑双正交db3作为母小波,对Y风场3月份的实测风速和NWP风速时间序列进行五层的尺度分解,提取低频分量,计算预测风速的系统偏差: (8) 式中,L表示低频分量。 选取预测时段T2=4 h,改变训练时段T1,按照式(8)计算每个样本的es_train和es_test,得到系统偏差序列Xs_train和Xs_test,由式(1)计算相关系数R。 图8 db3小波分解结果(M=5) T1/h1234812162024R0.910.840.780.710.350.290.250.230.19 可以看出随着T1的增长,R的值呈衰减趋势,当T1<3 h时,R1>0.8,表明在短期时间尺度内可以认为es基本保持不变,满足式(6),因此可以用线性方法对NWP风速进行校正。 考虑对比性,计算未经小波分解的系统偏差序列的相关系数。同样选取T2=4 h,改变训练时段T1,按照式(2)计算每个样本的es_train和es_test,得到系统偏差序列Xs_train和Xs_test,由式(1)计算相关系数R。 表3 不同T1对应的相关系数R 对于不同的T1,R的值均小于0.8,说明在短期时间尺度内es_train和es_test相关性较弱,不满足式(6)假设。 4.3 超短期风功率预测[7]和短期风功率预测对比分析 4.3.1 预测时段<4 h(超短期)的实例分析 研究对象为Y风场,数据采用该风电场2014年3月份全线风速数据及NWP 风速数据。图9给出了线性校正(含滤波)、线性校正(无滤波)、小波线性(含滤波)和小波线性(无滤波)的平均相对误差曲线,并以持续模型预测的风速和NWP风速的平均相对误差曲线作为衡量校正效果的标准。 图9 线性校正法平均相对误差曲线 由图9可以看出:小波线性(含滤波)的校正效果最好,可见仅针对低频平稳信号进行线性校正,消除了大气扰动和信号的干扰,提高了超风功率的预测精度。校正后的风速时间序列经滤波处理,可滤除病态方程求得的个别失真风速,进一步提高预测精度。 4.3.2 预测时段>4 h(短期)的实例分析 图10 小波线性(含滤波)校正误差曲线 针对不同的预测时段,小波线性(含滤波)模型的预测误差曲线如图10所示。由图10可以看出:a)随着预测时段的增长,预测误差逐渐增长;b)当预测时段超过4 h时,小波线性(含滤波)模型预测效果变差,这是因为预测时段超过4 h时,训练时段和预测时段的系统偏差序列线性相关性较低,因此该预测方法不适用于短期风功率预测。 采用小波多分辨分析法对实测风速时间序列和NWP风速时间序列进行多尺度的小波分解,滤除其高频分量,探索训练时段实测风速的低频分量和NWP风速低频分量之间的线性函数关系,并对预测时段NWP的低频分量进行线性校正。为了避免求解过程中出现的"病态"方程导致的数据失真,采用巴特沃兹低通滤波器校正后的风速时间序列进行滤波处理。实验结果表明,利用小波变换理论和单位置NWP的预测模型可有效地提高超短期风功率预测的精度,对进一步解决实际工程问题具有很好的指导意义。 [1] 杨 琦,张建华,王向峰,等.基于小波-神经网络的风速及风力发电量预测[J].电网技术,2009,33(17): 44-48. [2]王丽婕,冬 雷.基于小波分析的风电场短期发电功率预测[J].中国电机工程学报,2009,29(28): 30-33. [3]飞思科技产品研发中心.小波分析理论与 MATLAB7实现[M].北京: 电子工业出版社,2005. [4]汪小明,尹 笋,杨 楠,等.基于小波分解和ELMAN神经网络的风速-风功率预测研究[J].陕西电力,2014,9:720-724. [5]董长虹.Matlab小波分析工具箱原理与应用[M].北京: 国防工业出版社,2004. [6]李希强,王 笛,陆舍铭,等.皮尔逊相关系数与相结合研究烟用香精香料指纹图谱[J].精细化工,2008,25(5): 475-478. [7]Paras M,Hamidreza Z,William D R.Forecasting aggregated wind power production of multiple wind farms using hybrid wavele[J].Int.J.Energy Res,2014,38(13):1172-1178. (责任编辑 佟金锴 校对 张 凯) Research of Ultra-short-term Wind Power Forecasting Based on dbN Wavelet Transformation ZHONG Hong-yua,GAO Yangb,ZHONG Chaoa,TIAN Ming-huia,WU Lianga (a.Graduate Department;b.School of Electrical Engineering,Shenyang Institute of Engineering,Shenyang 110136,Liaoning Province) To reduce the non-stationary of wind speed sequence,the ultra-short-term wind power forecasting model based on dbN wavelet transform and NWP of single place is studied in this paper.Wavelet multi-resolution analysis which decomposes the original wind speed time series into different bands is used to filter out the high frequency component and obtain low frequency component,which can be a decisive role on wind power forecasting.Then,the ultra-short-term wind speed sequence is generated by linearity correction method mathematical model,and the data in the sequence is filtered with butterworth low-pass filter.The results show that this method can effectively improve the prediction precision of ultra-short-term wind power forecasting. Wavelet transform; ultra-short-term; filter; wind power forecasting 2015-04-30 钟宏宇(1986-),男,辽宁辽阳人,硕士研究生。 高 阳(1974-),男,辽宁沈阳人,副教授,博士,硕士生导师,主要从事电力系统自动化及新能源方面的研究。 10.13888/j.cnki.jsie(ns).2015.03.003 TM614 A 1673-1603(2015)03-0203-062 风速校正原理
3 滤波器的选定
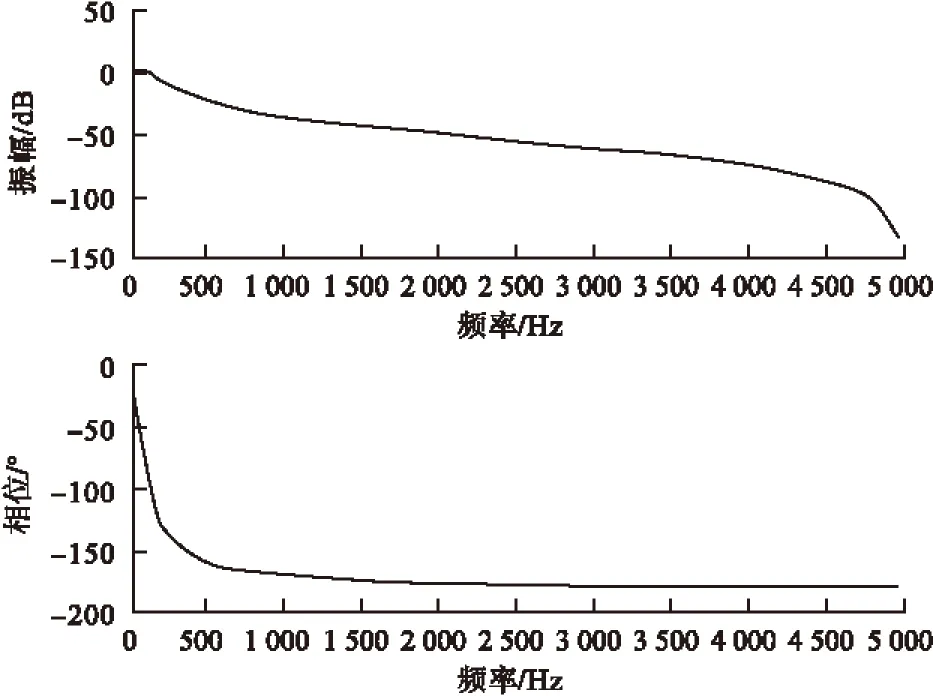


4 算例分析
v(i)=vmin,ifv(i)





5 结 语
