电磁学与电动力学中的磁单极—Ⅳ
2015-02-24王青
王 青
(清华大学物理系,北京 100084)
教学研究
电磁学与电动力学中的磁单极—Ⅳ
王 青
(清华大学物理系,北京 100084)
本文为作者磁单极系列文章的第4篇,该系列文章在电磁学和电动力学框架内用尽量科普的方式分别介绍磁单极的若干奇特性质.在本篇文章中作者讨论用拓扑参量θ描写磁电介质,发现在这种介质上出现了电荷与磁单极作为双荷子共生的现象.如果进一步考虑到磁荷与电荷的量子化,则得到此介质的拓扑参量θ必须是π的分数或整数倍.
磁电介质;拓扑;双荷子;磁单极
本文是在电磁学和电动力学中讲解磁单极奇妙性质的第4篇文章.在前3篇文章[1-3]中分别介绍了磁单极在角动量方面的角色和作用,狄拉克磁单极及其与规范变换的关系,以及磁单极在作用量中的作用;在本文中介绍磁单极在磁电介质中所起的作用.本篇内容安排如下: 先在第1节作为铺垫介绍真空中对给定电荷电流源的纯电磁场系统的作用量;然后在第2节利用电磁场的作用量介绍磁电介质;在第3节证明这种介质中的自由电荷和自由磁单极会发生共生现象,即产生所谓的“双荷子”,若进一步要求磁单极和电荷的量子化,磁电介质的参量必须有所限制.
1 真空中的电磁场作用量
如在上一篇文章[3]中所介绍的,绝大部分的物理系统都可以利用最小作用量原理来描写,即使在有磁单极存在的情形下,作用量也是存在的,虽然这时要求作用量与磁单极相关的部分要向非物理区域扩展.我们先从真空中对给定电荷电流源的纯电磁场系统的作用量开始讨论.为明显反映计算的洛伦兹协变性,将在闵科夫斯基空间进行讨论,其中时空坐标用时空中的4矢量xμ代表,脚标μ的1,2,3分量合起来代表普通的空间坐标r,第4个分量是ict即复数i及光速c与时间t的乘积;而对时空坐标的微商用4矢量∂μ代表,其中脚标μ的1,2,3分量合起来代表对普通的空间坐标的微商,第4个分量是;电磁势用Aμ表达,前3个分量是普通的矢量势A,第4个分量是其中φ是通常的标量势.4度的电流密度用jμ表达,前3个分量是普通的电流密度j,第4个分量是icρ,其中ρ是通常的电荷密度.利用电磁势可以进一步定义二阶场强张量Fμ ν
由于有两个分别可取4个值的角标μ和ν,此二阶张量共有16个分量,在式(1)的右边把这16个分量排成了一个4×4矩阵,并利用标准的电场强度与标量势和矢量势的关系E=-及磁感应强度与矢量势的关系B=×A,把矩阵元用电场强度和磁感应强度表达出来了.式(1)定义的场强张量Fμ ν满足如下方程:
这个方程非平庸的分量是真空中麦克斯韦方程组中的两个无源方程:
利用电磁势Aμ、场强张量Fμ ν和4度的电流密度jμ,可以写出给定的电荷电流源(用jμ描写)下的纯电磁场系统的作用量S
其中μ0是真空的磁导率.时间积分dt和空间积分dV遍及整个时空.注意上式如果用习惯使用的电场强度、磁感应强度、电荷密度、电流密度、标量势和矢量势来表达则为
将式(4)给出的作用量对电磁势Aμ求极值,得到方程
它的前3个分量和第4个分量分别给出真空中麦克斯韦方程中含源的两个方程
其中ε0是真空的介电常数,它与前面引进的真空的磁导率μ0及光速c的关系为

其中εμ ν σ ρ是四阶全反对称张量,它在其4个指标分别取1,2,3,4及其偶数次置换时取值为1,奇数次置换时取值为-1,其他(2个、3个或4个指标取相同的值)为零.原则上这个项前还可以乘上一个任意常数.之所以没有把式(9)所给的项加进作用量式(4),是因为式(9)的右边第二个表达式,它把这一项表达为一个对时空坐标的全微商,利用体积分和面积分的互换关系,这项只有在时空的边界上才有贡献.通常把时空边界上的电磁势取为零,因此这项对作用量没有贡献.注意这种只依赖于边界的项通常在区域中有拓扑非平凡的场时会有贡献,只是在真空中的电磁场在数学上可以证明总是拓扑平凡的,因此这项没贡献.
2 磁电极化介质的作用量
在上节说明了式(9)所引进的项在真空中对作用量没有贡献.如果考虑具有某种拓扑非平凡性质的介质,则式(9)所代表的项对此介质可以不为零.由此考虑某种特殊的介质,其对应的作用量为

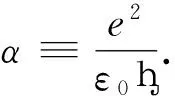
上式中为了得到第二个等号,利用了麦克斯韦方程中的法拉第电磁感应定律式(3)中的第二个式子.从式(12)中可以读出极化导致在此介质上极化电荷为
为了得到第二个等号,利用了麦克斯韦方程中的无磁单极的方程(3)中的第一个式子.结合电磁学电动力学中的极化强度P和磁化强度M与ρ′和j′的关系
注意对均匀介质(θ为常数),ρ′和j′都只出现在介质的表面,j′还会出现在介质出现或消失的那个瞬间.将式(15)与式(13)和(14)进行对比,得到对此介质有
它们就是这种介质的电磁性质方程.注意在通常的介质中,极化强度P是由电场强度E驱动的,磁化强度M是由磁感应强度B驱动的,而对此介质却反过来了,极化强度P是由磁感应强度B驱动的,磁化强度M是由电场强度E驱动的.具有这种扭曲的极化和磁化效应的介质叫磁电介质.它是近些年来凝聚态物理和材料科学的热门前沿研究课题,人们在努力寻找和构造具有大的磁电效应(相当于大的θ值)的磁电介质.
3 磁电介质中的双荷子
上节引进了一种磁电介质.并且知道如果这个介质是均匀极化和磁化的(也就是介质上的θ保持为常数),介质中是没有极化和磁化导致的电荷和电流的.现在讨论如果在均匀极化和磁化的介质上通过某种方法加入了自由电荷或磁单极,看看会发生什么现象.为简单起见,考虑介质上的j=0,这时式(11)简化为
在上式两边同时取散度,方程左边为零,方程右边给出
注意到介质上某处体积V内的电荷q和磁荷(磁单极)g可以通过计算此体积上电场强度和磁感应强度的通量计算出来
将式(18)对体积V进行积分,并代入式(19),得到

进一步如果引入第1篇文章[1]中关于磁荷g与电荷e的量子化结果ge=±4πn,则式(21)可以进一步化为
也就是我们预言在这种介质上的电荷是电子电荷乘以一个系数θ/π的整数倍.如果进一步要求电荷都必须是电子电荷的整数倍(例如q/e=m),则这种介质的θ参量必须是π的分数或整数倍.通常这只有依靠量子场论的反常计算才能得到的结论,现在我们在电磁学和电动力学中得到了.在现实世界,近年来被热炒的拓扑绝缘体就是其中的一种,它满足θ=π.
4 结语
存在一种用拓扑参量θ描写的磁电介质,此种介质上,电荷与磁单极共生形成双荷子.如果进一步考虑到磁荷与电荷的量子化,拓扑参量θ必须是π的分数或整数倍.
[1] 王青.电磁学与电动力学中的磁单极-Ⅰ[J].物理与工程,2013,23(6):8-11.
[2] 王青.电磁学与电动力学中的磁单极-Ⅱ[J].物理与工程,2014,24(5):29-33.
[3] 王青.电磁学与电动力学中的磁单极-Ⅲ[J].物理与工程,2015,25(4):19-24.
■
MAGNETIC MONOPOLE IN ELECTROMAGNETISM AND ELECTRODYNAMICS—Ⅳ
Wang Qing
(Department of Physics,Tsinghua University,Beijing 100084)
This is the forth paper in the series of magnetic monopole.These series include four individual papers,in which some peculiar properties of magnetic monopole will be introduced as popular science in the frameworks of electromagnetism and electrodynamics.In this paper,we discuss magnetoelectric media described by topological parameterθ,prove the coexistence of charge and monopole as dyon.If further introduce the quantization of charge and monopoles,we show that topological parameterθmust be fraction or integer times π.
magnetic monopole;magnetoelectric media;topology;dyon
2015-05-21
王青,男,教授,主要从事理论物理的科研和教学工作,研究方向为量子场论与基本粒子理论.wangq@mail.tsinghua.edu.cn
