Dempster合成规则的等效计算方法及其实现
2015-02-24李文艺吕现钊郝保明
李文艺, 吕现钊, 郝保明
(宿州学院 机械与电子工程学院,安徽 宿州 234000)
Dempster合成规则的等效计算方法及其实现
李文艺, 吕现钊, 郝保明
(宿州学院 机械与电子工程学院,安徽 宿州 234000)
摘要:给出了Dempster合成规则的一种等效计算方法,该方法能够由非归一化的合成结果直接计算出最终的合成结果,同时在整个合成的过程中避开了冲突系数的计算.针对该方法给出了一种简单的实现途径,首先利用二进制编码数据表示辨识框架幂集中的元素;然后把Dempster合成规则中集合的运算转化为二进制编码数据之间的逻辑运算;最后通过算例进行了验证,结果表明该方法与Dempster合成规则得到的结果完全相同.
关键词:证据理论;等效算法;二进制编码;冲突系数
证据理论源于上世纪60~70年代,该理论是由Dempster首先提出,后来由他的学生Shafter进行了完善和发展,所以证据理论又称为D-S证据理论[1,2].由于证据理论可以很好的表示客观世界中的信息,并能够区分命题的“不确定”与“不知道”之间的关系,该理论已经是模式识别、信息融合等领域的重要方法[3-5].证据理论的核心是Dempster合成规则,该规则可以把不同的证据进行合成,从已有的证据生成新的证据.在一般情况下利用Dempster合成规则可以使正确信息逐步聚集,从而合成结果有利于进行最终的判断与决策.但是在使用Dempster合成规则进行多个证据融合时,计算量会随证据个数的增加而急剧增大;在进行多个证据的融合过程中,计算信任函数与冲突系数时要进行集合之间的“交”运算,而大量集合之间的“交”、“包含”运算会耗费较多的计算时间.以上这些因素都影响到了证据理论的应用[6].
针对证据理论计算量大的问题,本文给出了Dempster合成规则的一种等效计算方法,与经典的Dempster合成方法相比本文所给出的方法计算量较小、易于计算机实现.该方法利用二进制编码表示辨识框架幂集中的元素;由此可以把证据理论中集合之间的“交”运算转换成了二进制编码之间的“与”逻辑运算.然后利用Dempster等效合成公式计算最终的融合结果.对实验分析表明该方法的计算量有所减小,计算结果与Dempster方法完全一样.
1证据理论
非空集合Θ由一些互斥且可穷举的元素组成,称Θ为辨识框架.集合Θ表示人们对某一问题所有可能结论(或所有可能假设)的集合;从而,所需要解决的问题转化为Θ的子集.


(1)


(2)
似真函数表示不反对命题的程度,似真函数的计算方法为
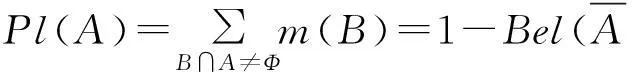
(3)

2Dempster合成规则的等效计算方法
假设m1,m2为辨识框架Θ下的两个基本概率赋值函数,A1,A2,…,AN表示基本概率赋值函数m1的焦元;B1,B2,…,BM表示基本概率赋值函数m2的焦元.利用Dempster合成规则合成之后的基本概率赋值函数记为m;C1,C2,…,CK表示合成结果的焦元.
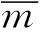

(4)
公式(4)中Cl≠Θ;i=1,2,…,N;j=1,2,…,M;l=1,2,…,K),最终的融合结果可以按一下方法计算:

(5)
公式(5)中(l=1,2,…,K).下面证明该计算方法与经典的Dempster合成规则是等价的.
证明
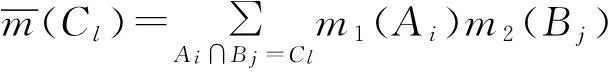
(6)

(7)
因此,得:

(8)
由证据理论的基本要求:
m(C1)+m(C2)+…+m(CK)=1.
(9)

(10)

(11)
所以:

(12)
因此,得到:

(13)
证毕.
由以上可知本文所给出的方法方法与Dempster合成规则是完全等效的,而不是一种近似的计算[7,8].
3等效计算的实现
利用Dempater合成规则需要判断集合之间的关系是否满足运算条件.为了避免集合之间的运算,本文给出了一种新的实现方法,该方法中利用二进制编码之间的“与”逻辑运算代替集合之间的“交”运算.本文的基本思想为:若辨识框架Θ中有N个元素,则Θ的幂集2Θ中最多有2N个元素,而一个N位的二进制数最多可以表示2N种不同的组合.可以用N位的二进制数据表示辨幂集中的2N个不同的元素.下面通过一个实例说明本文方法的基本思想.
例:假设Θ={a,b,c},Θ的幂集共有8个元素分别为Φ,{a},{b},{c},{ab},{bc},{ac},{abc}这8个元素分别用二进制表示为:000,100,010,001,110,011,101,111.m1,m2表示辨识框架Θ下的两个基本概率赋值函数.使用二进制编码之后,使用Dempster合成方法进行计算,合成结果可用已下方法计算:
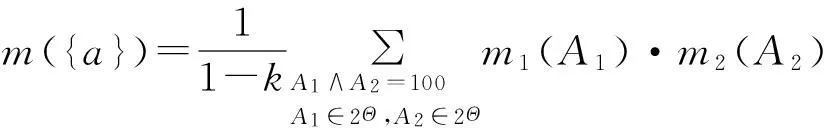







当辨识框架中的元素较多时,只需要增加二进制编码的位数即可.Dempster合成规则转换为以下表达式:

(14)

针对上述例题,利用本文所给出的方法可按照已下方法进行计算.






分别表示未归一化之后的融合结果.则:
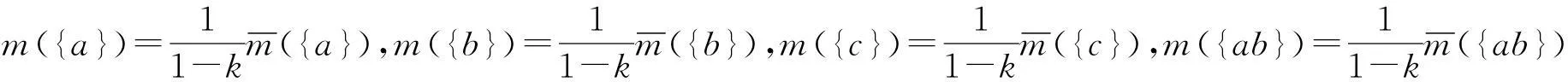

则最终的融合结果可表示为


通过分析知,在Dempster合成规则中原来集合的“交”运算变成了逻辑“与”运算.按照此方法式(4)可以表示为
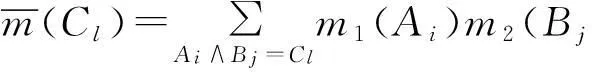
(15)
用二进制编码的方法实现证据融合的步骤为
步骤1:对幂集中的每个元素进行二进制编码.
步骤2:按式(14)计算出未归一化的融合结果.
步骤3:按式(5)计算出最终融合结果.
4算例仿真
为了比较本方法与经典的Dempster方法,下面通过一个具体的算例进行仿真实验.假设有6个不同的传感器探测到了飞行器类型,分别用ABC表示,A=“战斗机”,B=“轰炸机”,C=“武装直升机”.从6个传感器得到的基本概率分配函数分别为m1,m2,m3,m4,m5,m6,函数值如表1所示.

表1 基本概率分配函数值
利用本文方法与Dempster合成规则得到的结果是相同的,融合结果是:
m(A)=0.573 6,m(B)=0.350 8,m(C)=0.070 7,m(AB)=0.001 2,m(BC)=0.003 7.
本文所给出的方法用二进制编码表示了原来的集合,利用了二进制之间的逻辑运算代替了原来的集合之间的运算.另外本文所给出的方法避免了冲突系数的计算,针对本算例来说由于不用计算冲突系数,使得本文的计算量为经典Dempster合成规则的约70%,计算量有所减少.
5结语
给出了Dempster合成规则的一种等效计算方法,该方法可以避免计算证据之间的冲突系数,而可以得到与原方法相同的结果,与原方法相比本文的计算量有所减少.同时,文中对所给出的方法进行了证明.针对文中所提出方法的实现问题,文中利用二进制的方法对辨识框架的幂集中的元素进行编码.然后利用逻辑运算代替Dempster方法中集合之间的运算.用二进制编码对辨识框架进行重新表示之后,可以更加方便的利用计算机编程的方法实现多个证据的合成问题.仿真实验表明该方法可以较好的解决多证据的融合问题,并能够得到与Dempster方法相同的融合结果.
参考文献:
[1]Dempster A P. Upper and lower probabilities induced by a multi-valued mapping [J].Annuals of Mathematics Statistics, 1967,38(4):325-339.
[2]Shafer G. A Mathematical Theory of Evidence [M].Princeton: Princeton University press,1976.
[3]王凤朝,刘兴堂,黄树采.基于模糊证据理论的多特征目标融合检测算法[J].光学学报,2010,30(3):713-719.
[4]张燕君,龙呈.基于证据理论的目标识别方法[J]. 系统工程与电子技术,2013,35(12):2467-2470.
[5]王峰. D-S证据理论在指纹图像分割中的应用研究[J].计算机工程与应用,2010,46(24):169-172.
[6]陈圣群,王应明.证据的分组合成法[J]. 控制与决策,2013:28(4):574-578.
[7]王壮,胡卫东,郁文贤,等.基于截断型D-S的快速证据组合方法[J].电子与信息学报,2002 ,24(12):1-3.
[8]李岳峰,刘大有.证据理论中的近似计算方法[J].吉林大学学报,1995,31(l):28-32.
An Equivalent Algorithm of the Dempster Combination
Rule and Its Realization
LI Wen-yi, LV Xian-zhao, HAO Bao-ming
(SchoolofMechanicalandElectronicEngineering,SuzhouUniversity,Suzhou234000,China)
Abstract:An equivalent algorithm of the Dempster combination rule is presented in this paper. By this algorithm, the final result can be obtained from the un-normalized combination results, and the calculation of the conflict coefficient can be avoided at the same time. A realization approach of this method is further presented. Firstly, each element of the discernment frame is coded by the binary encoding, and then the computation of sets is transformed into logic computation of the binary encoding in the Dempster combination rule. At last, calculation examples are used to test this new method, and findings show that the results obtained are the same to those obtained by the Dempster combination rule.
Key words:evidence theory; identical algorithm; binary encoding; conflict coefficient
责任编辑:赵秋宇
中图分类号:TP391
文献标识码:A
文章编号:1671-9824(2015)02-0065-05
作者简介:李文艺(1980—),男,河南开封人,讲师,硕士,研究方向:模式识别、信息融合.
基金项目:安徽省高等学校省级优秀青年人才基金重点项目(2013SQRL084ZD);宿州学院基金项目(2009yss08,2009yss07,szxyjyxm201307)
收稿日期:2014-05-27
