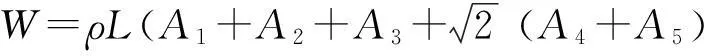基于空间相关元模型的机械设计优化研究

胡万强

(许昌学院 电气工程学院，河南 许昌 461000)

基于空间相关元模型的机械设计优化研究

胡万强

(许昌学院 电气工程学院，河南 许昌 461000)

摘要：简述了全局近似空间相关元模型的研究历程，详细介绍了空间相关元模型的建模过程.在二元素框架结构设计优化中，使用空间相关元模型为该结构建立一个有利于计算机分析的近似模型，进而测试空间相关元模型的预测能力.仿真结果证明，这些空间相关元模型能够在全局近似优化设计中产生一个满足精度要求的近似结果.

关键词：结构设计；全局近似；空间相关元模型

由于现代机电产品结构越来越复杂，对其仿真时则耗费越来越多的计算机资源.尽管计算机技术日新月异，计算速度越来越快，但仍不能满足工业对仿真分析的需求.因此，为了应对工业发展的巨大挑战，在过去近10年中，一种“模型的模型”—元模型应运而生并得到广泛应用，元模型方法是指利用实验设计所产生的空间采样点来构建简化近似模型代替复杂的仿真目标模型从而进行优化分析的一种优化方法，该方法促进了优化和概念搜索的发展，能在不影响仿真目标精度的前提下减少优化迭代的次数，从而减少对计算机资源的消耗[1].

本文的目的，就在于利用元模型理论与算法，通过实例分析，研究如何通过少量采样点来构造高精度元模型，为工业中结构设计优化提供一种新的思路与方法.

1空间相关元模型[3]

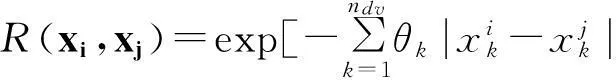
通过最大化表达式得到前面公式中θk的最大似然估计为

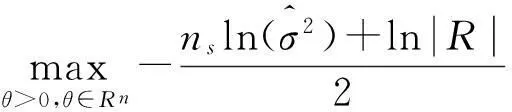
这常常被用来拟合该模型.验证任意θk值建立的插值模型可通过交叉验证或通过额外验证点计算相关误差这两种方法来实现.

2工程实例分析

图1　五杆平面桁架结构

对于全局近似问题，文章选择五杆平面桁架结构来测试验证空间相关元模型的估计能力.五杆平面桁架结构如图1所示，主要特性参数：杨氏模量E=7 030.8×107N/m2，密度ρ=27 680.37 N/m3，许用应力σa=±1.7577×108N，设计变量为每根杆的截面区域，其定义范围为

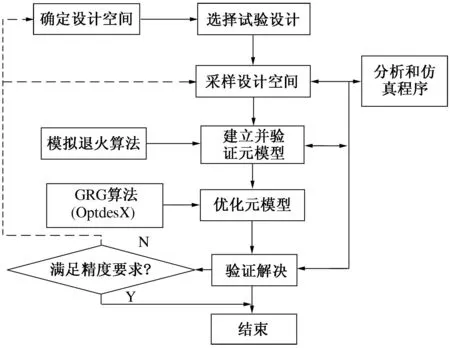
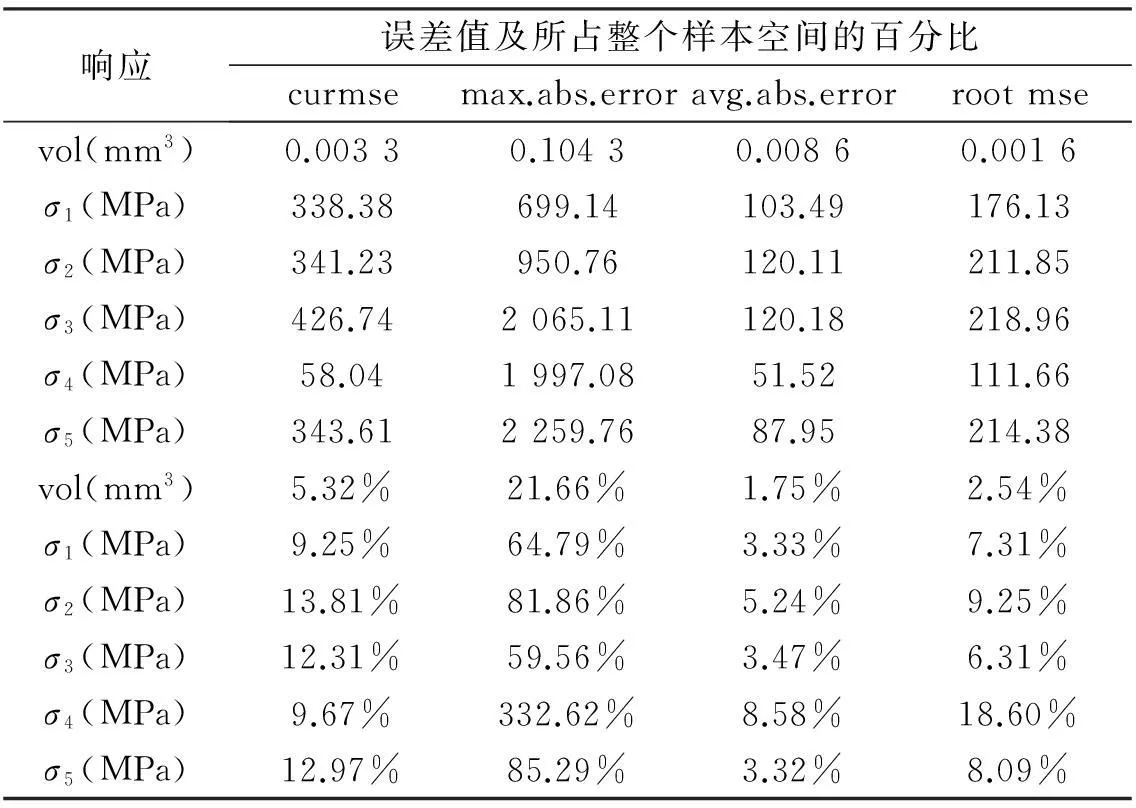
{64.516 mm2

(1)

在满足五杆平面桁架结构屈服强度和稳定性条件的前提下，优化目标为最小化桁架的承载值.经分析可知，其函数为

(2)

上式(2)中，L=9.144 m，每根杆上的应力要小于σa，即：

{-1.757 7×108N<σi<1.757 7×108N}i=1,2,3,4,5.

(3)

经计算，当A1=0.002 541 m2，A2=0.000 064 516 m2，A3=0.000 064 516 m2，A4=0.003 592 9 m2，A5=0.000 064 516 m2时，W的最优值为1 984.862 88.下面，文章将利用空间相关元建模替代公式(1)和公式(3)来重复这个结果.

图2　元建模策略流程图

3五杆平面桁架结构仿真

对上述的五杆平面桁架结构建立的元建模策略如图2所示.首先，选择一个实例来采样设计空间中的点，然后利用最大最小的拉丁超立方设计和随机正交矩阵来采样设计空间[4].接下来就是通过调用近似分析代码或者仿真程序来实现对每个采样点的实际空间采样，针对问题中的每一个响应建立一个元模型，并确定θk的最大似然估计.由此产生的最佳解决方案在元模型中得以验证.

五杆平面桁架问题的49采样点由随机7水平的正交矩阵得到[5,6]，每个响应的负载值和σi的最大最小值见表1所示.

表1　五杆平面桁架σi值

采样点的区域为[0,1]，拟合每个响应空间的相关元模型的θk值的最大似然估计值见表2所示.此例中值得注意的是文章建立了自身独有的应力模型，而不是实际的限制值.这样做的目的是可以不必拟合应力限制条件，从而减少空间相关元模型的数量.

表2　五杆平面桁架θk值的最大似然估计值

五杆平面桁架的验证结果见表3所示，除了留一交叉验证均方根误差，其他验证均为基本随机拉丁超立方的2 500个点.平均绝对误差和均方根误差所占空间的百分比效果很理想，但对于最大绝对误差来讲，却又有很大差异，它能够说明平均绝对误差和均方根误差所占空间的百分比在2%～10%之间.大的差异出现在不可行设计区域，因此需要继续验证优化，以希望得到更精确的元模型估计.

表3　五杆平面桁架元模型验证结果

通过继续优化，得到的相应空间相关元模型得到的最小负载和应力值见表4所示.表中包括空间相关元模型得到的验证负载以及上述中的已知最优值.

表4　五杆平面桁架元模型优化验证结果

从表中可以看出，获取的最优值是相当接近实际最优值的.与实际优化值相比较，估计最优负载控制在实际最优负载的-2.23%之内，而5个应力值中有3个控制在0.81%之内甚至更好.对于σ2和σ3的估计应力精度稍差，分别比实际变化率61.11%和15.24%.幸运的是，在最优点附近，没有一个约束条件是具有约束能力的.

4结语

在上述五杆平面桁架优化设计中，文章成功地建立并使用空间相关近似模型去获取非常接近实际值的估计最优值，从而展示了空间相关元模型在全局近似中优化方面的有效性.所以说，空间相关元建模是一种值得考虑并有很大研究前景的方法.随着研究的深入，通过空间相关函数的选择和实验设计的讨论，一定能够很好地改善空间相关元建模的精度和效率.

参考文献：

[1]Dyn N, Levin D, Rippa S. Numerical procedures for surface fitting of scattered data by radial basis functions[J].SIAM Journal of Scientific and Statistical Computing, 1986,7(2) :639-659.

[2]Jin R, ChenW, Sudjianto A.An efficient algorithm for constructing optimal design of computer experiments[J].Journal of Statistical Planning and Inferences， 2005,134(1) :268-287.

[3]Booker A J, Conn A R, Dennis J E, et al. Global Modeling for Optimization: Boeing/IBM/Rice Collaborative Project [R]. ISSTECH-95-032, The Boeing Company, Seattle,WA, 2000.

[4]游海龙,贾新章.基于遗传算法的Kriging模型构造与优化[J].计算机辅助设计与图形学学报,2007(19):64-66.

[5]Osyczka A. Multicriteria optimization for engineering design[J]. Design optimization, 2004,(5):193-227.

[6]魏昕.基于元模型的全局优化算法研究[D].武汉：华中科技大学,2012.

Research on Machine Design Optimization Based on Spatial

Correlation Metamodels

HU Wan-qiang

(SchoolofElectricalEngineering，XuchangUniversity,Xuchang461000,China)

Abstract:In the paper, the research process of metamodel is described and the modeling process of spatial correlation metamodels is introduced in detail. In the design optimization process of two bar truss structure, spatial correlation metamodels are used to establish an approximation model for computing analysis, and the predictive capability of spatial correlation metamodels is tested. The simulation results show that these spatial correlation metamodels can produce sufficient accuracy for optimization when used as global approximations.

Key words:structural design; global approximation; spatial correlation metamodels

责任编辑：赵秋宇

中图分类号：TP273

文献标识码：A

文章编号：1671-9824(2015)02-0035-04

作者简介：胡万强(1975—)男，河南渑池人，副教授，硕士，研究方向：机电设计及其控制.

基金项目：河南省教育厅高等学校重点科研项目(15A460043)；许昌学院科研基金项目(2015072)

收稿日期：2014-01-23