非线性湿气迁移方程的非协调元的超收敛分析

樊明智, 王芬玲

(许昌学院 数学与统计学院，河南 许昌 461000)

樊明智, 王芬玲

(许昌学院 数学与统计学院，河南 许昌 461000)

摘要：在半离散格式下研究了非线性湿气迁移方程的非协调有限元逼近问题.利用该有限元的相容误差在能量模意义下可以达到O(h2)比其插值误差高一阶的特殊性质, 再结合高精度分析和平均值技巧导出了O(h2)阶的超逼近性，进而运用插值后处理技术得到了超收敛结果.

关键词：非线性湿气迁移方程；非协调元；超逼近；超收敛

0引言

考虑如下的非线性湿气迁移方程[1]

(1)

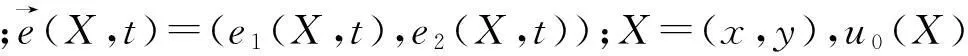
(i) 存在正常数a0、a1、b0、b1、f0、f1、e1使得X∈Ω、t∈(0,T]满足

(ii)g(u,X)关于u满足Lipschitz条件.

设Th为Ω上的一族均匀矩形剖分, 定义单元K的中心为(xk,yk), 其边长分别为2hx,2hy,h为K的最大直径,单元K的顶点为

a1(xK-hx,yk-hy)、a2(xK+hx,yk-hy)、a3(xK+hx,yk+hy)、a4(xK-hx,yk+hy),

∑={vi,i=1,2,3,4,5}, P=span{1,x,y,x2,y2},

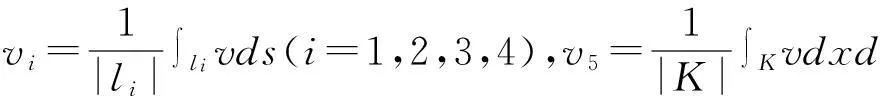
Vh={vh∶vh|K∈P,∫F|vh|ds=0,F⊂∂K,∀K∈Th},

其中[vh]表示vh跨过单元边界F的跳跃度, 当F⊂∂Ω时,[vh]=vh.

设Ih:u∈H1(Ω)→Ihu∈Vh为由Vh所诱导的插值算子, 满足

Ih|K=IK,∫li(IKu-u)ds=0(i=1、2、3、4),∫K(IKu-u)dxdy=0.

在[5]和[6]中证明了下面的重要结论.

引理1对任意vh∈Vh,φ(X,t)是关于X光滑函数, 有

(▽h(u-Ihu),▽hvh)h=0,

(2)

(3)

考虑问题(1)的相应变分问题为：

(4)

式(4)的离散问题为：求uh∈Vh, 使得对任意vh∈Vh满足

(5)

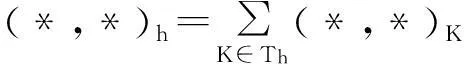
2超逼近和超收敛分析

定理1设u,uh分别为(4)和(5)的解,u、ut∈H3(Ω)，则有超逼近结果

证明记uh-u =(uh-Ihu)-(u-Ihu)=θ-η,∀vh∈Vh, 由(4)和(5)得

a(t)(▽hθt,▽hvh)h+b(t)(θt,vh)h+(f(X,t)▽hθ,▽hvh)h

=a(t)(▽hηt,▽hvh)h+b(t)(ηt,vh)h+(f(X,t)▽hη,▽hvh)h+

(6)

在(6)中取vh=θt得

=a(t)(▽hηt,▽hθt)h+b(t)(ηt,θt)h+(f(X,t)▽hηt,▽hθt)h+

(7)

下面逐项对A1～A8进行估计.

根据引理1中的(2)得A1=0,由Cauchy-Schwartz不等式和插值理论得

首先，进行残差检验，对修正后模型实施哈维检验，收尾概率=0.196 1，大于显著性水平5%，所以接受原假设，残差不存在异方差性，参数估计是有效的；其次，进行参数检验，在1%的显著性水平上，a0、a1和a2的P值均小于0.01，说明公式(3)中待估参数都是显著的；再次，进行模型整体检验，在1%的显著性水平上，F统计量对应的P值也小于0.01，说明方程的整体线性是显著的，样本可决系数R2=0.992，接近1，说明方程的拟合程度较好。

(8)

利用(8)和引理1中的(2)得

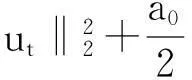
基于[21、22]中已给出的结论(β·▽η,vh)≤Ch2‖u‖3‖vh‖0,β是常数.再结合引言中假设(i)和式(8)得

|A4| =|(e1(X,t)ηx,θt)+(e2(X,t)ηy,θt)|

另一方面, 由[23]得

‖vh‖0≤C‖vh‖h.

再借助于引言中假设条件(ii)得

由假设(i)得

(9)

将A1～A8的估计和式(9)代入到式(7)得

(10)

对式(10)的两端从0到t积分, 并注意到θ(X,0)=0,得

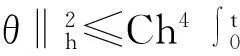
因此, 由Gronwall引理得

(11)

从而定理1得证.

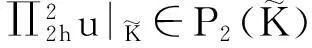
(12)

(13)

(14)

(15)

定理2在定理1的条件下有

证明根据定理1和(13)～(15)得

≤C‖uh-Ihu‖h+Ch2‖u‖3

定理2得证.

参考文献：

[1]施明德.非线性湿气迁移方程的初边值问题[J].应用数学学报,1990,13(1):31-38.

[2]陈宁,李崇新.具Sobolev-Galpern型湿气迁移方程解的渐近性和Blow-up[J].生物数学学报,2002,17(3):305-310.

[3]涂慧, 刘超，江成顺.一类二维湿气迁移模型的理论分析及数值模拟[J].信息工程大学学报,2005,6(1):19-22.

[4]裴丽芳,亢金轩,许超.非线性湿气迁移方程Carey非协调元逼近[J].河南科技大学学报,2011,32(6):81-84.

[5]LinQ,TobiskaL,ZhouAH.SuperconvergenceandextrapolationofnonconformimgloworderfiniteelementsappliedtothePoissonequation[J].IMAJournalNumericalAnalysis,2005,25(1):160-181.

[6]ShiDY,MaoSP,ChenSC.Ananisotropicnonconformingfiniteelementwithsomesuperconvergenceresults[J].JournalComputationalMathematics,2005,23(3):261-274.

[7]ShiDY,WangHH,DuYP.AnanisotropicnonconformingfiniteelementmethodforapproximatingaclassofnonlinearSobolevequations[J].JournalComputationalMathematics,2009,27(2-3):299-314.

[8]ShiDY,WangHH,GuoC.AnisotropicrectangularnonconformingfiniteelementanalysisforSobolevequations[J].AppliedMathematicsMechanics,2008,29(9):1203-1214.

[9]石东洋,谢萍丽.Sobolev方程的一类各向异性非协调有限元逼近[J].系统科学与数学,2006,29(1):116-128.

[10]ShiDY,RenJC.NonconformingmixedfiniteelementapproximationtothestationaryNavier-Stokesequationonanisotropicmeshes[J].NonlinearAnalysis,Theory,MethodsandApplications,2009,71(9):3842-3852.

[11]石东洋,毛士鹏.三维Stokes问题各向异性混合元分析[J].应用数学学报,2006,29(3):502-517.

[12]ShiDY,WangL.Ananisotropicnonconformingfiniteelementschemewithmovinggridsforparabolicintegro-differentialequations[J].JournalSystemsScienceandComplexity,2011,24:1020-1032.

[13]石东洋,郭诚,王海红.带弱奇异核的抛物积分微分方程的非协调有限元方法[J].数学物理学报,2010,30A(3):764-775.

[14]ShiDY,WangXL.Aloworderanisotropicnonconformingcharacteristicfiniteelementmethodforaconvection-dominatedtransportproblem[J].AppliedMathematicsComputation,2009,213(2):411-418.

[15]石东洋,张斐然.Sine-Gordon方程的一类非协调有限元分析[J].计算数学,2011,33(3):289-297.

[16]ShiDY,MaoSP,ChenSC.Alocking-freeanisotropicnonconformingfiniteelementforplanarlinearelasticityproblem[J].ActaMathematicaScientia,2007,27B(1):193-202.

[17]石东洋,王慧敏.非线性双曲型积分微分方程的各向异性非协调有限元逼近[J].工程数学学报,2010,27(2):277-282.

[18]石东洋,郝颖.广义神经传播方程的一个各向异性非协调有限元逼近[J].生物数学学报,2009,24(2):279-286.

[19]石东洋,关宏波.抛物型变分不等式的一类全离散非协调有限元方法[J].应用数学学报，2008,31(1):90-96.

[20]许超,周家全,张永胜.Sobolev-Galpern型湿气迁移方程各向异性非协调有限元分析[J].西北师范大学学报,2011,47(1):34-37.

[21]LinQ,WangHong,ZhangShuHua.Uniformoptimal-orderestimatesforfiniteelementmethodsforadvection-diffusionequations[J].JournalSystemsScienceandComplexity,2009,22(4):555-559.

[23]石东洋,张熠然.非定常Stokes问题的矩形Crouzeix-Raviart型各向异性非协调元变网格方法[J].数学物理学报,2006,26A(5):659-670.

NonlinearMoistureTransferEquation

FANMing-zhi,WANGFen-ling

(School of Mathematics and Statistics, Xuchang University, Xuchang 461000, China)

Abstract:An nonconforming finite element approximation for nonlinear moisture transfer equation is studied under the semi-discrete scheme. By using the specific feature that the consistence error of this element can reach o(h2) under energy fuzziness, which is one rank higher than its interpolation error, and by using high accuracy analysis and mean-value technique, the super approximation of o(h2) is derived, then the superconvergence result is obtained through interpolated post processing technique.

责任编辑：周伦

中图分类号：O242.21

文献标识码：A

文章编号：1671-9824(2015)02-0001-05

作者简介：樊明智(1969—),男,河南鄢陵人,教授,硕士,研究方向：有限元方法及其应用.

基金项目：河南省教育厅自然科学基金项目(14A110009)；许昌市科技发展计划项目(1404010)

收稿日期：2014-09-11