模糊理论在路基边坡防护方案优选中的应用

陈　平

( 重庆市设计院　重庆　400015)

模糊理论在路基边坡防护方案优选中的应用

陈平

( 重庆市设计院重庆400015)

摘要根据影响路基边坡防护方案决策的定量指标和定性指标，建立各指标的模糊有序判断矩阵，有效组合主、客观权重，建立以工程模糊集理论为基础的路基边坡防护方案优化模型。并以某实际路基边坡防护方案的选择为例进行计算，结果表明，模型能够减少目标的客观权重与实际情况之间的误差，较易体现专家的意见且符合工程客观实际。该方法计算量小，适应性强，对其他综合评价也有一定的借鉴意义。

关键词路基边坡防护模糊理论方案优选权重

路基边坡坡面防护的目的主要是保护路基边坡表面不受降水、日照、气温、风力等自然力的破坏，从而提高边坡的稳固性。现阶段路基边坡坡面防护的主要措施多种多样，而影响路基边坡防护方案决策的主要因素有：安全稳定性、施工可行性、经济合理性，以及环保美观性等，其中每个影响因素的影响程度不同，尤其是安全稳定性，是在边坡防护方案决策时首先考虑的因素，其次是经合理性、施工可行性和环保美观性。如何选择技术可靠，经济合理且安全适用的边坡防护方案具有重大的理论和现实意义。由于边坡地质状况的复杂性以及各种防护措施的特殊性，其最优决策方案的确定受较多因素的影响，只有有效组合主、客观权重，才能得到较为客观、系统的最优化决策方案。为此，本文针对路基边坡处理方案，提出建立在模糊集理论[1]上的路基边坡防护方案优化法，确定评价因素及其隶属函数，对路基边坡防护方案的效果进行综合评价，选择最优的路基防护处理方案。

1防护方案处理模糊集优化模型的建立

1.1　确定有序模糊判断矩阵

设有n个方案，X={X1,X2,…,Xn} ,每个方案有m个评价指标(目标)，记为A={A1,A2,…，An}。对目标集A就重要性进行二元比较，得到二元比较排序一致性标度矩阵。在标度矩阵的基础上就目标的重要性再次进行二元比较，得到有序模糊判断矩阵[2-4]。

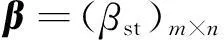
(1)

式中：二元比较模糊标度βst与语气算子之间的关系见表1[5]。

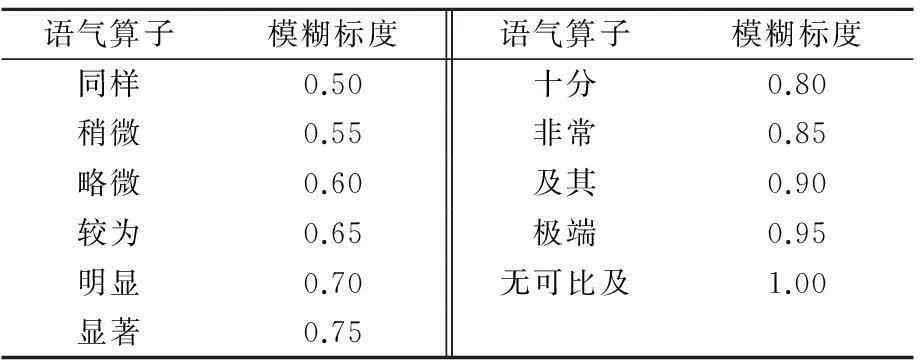
表1　语气算子与定量标度之间的关系

1.2　治理方案优化的设计模型

方案的优劣程度依据m个目标特征值，按从优级到劣级的C个级别进行识别。对于任一目标就模糊概念优而言，可以规定优级(1级)对优的相对优属度为1，劣级( c级)的相对优属度为0。由于模糊概念优在中介过渡阶段出现的渐变性，可以认为1级至c级的相对优属度从0~1呈级性递增，前后2个级别的优属度递增差值Δ=1/c-1，对于任一目标，从1级到c级各级别的相对优属度标准向量为

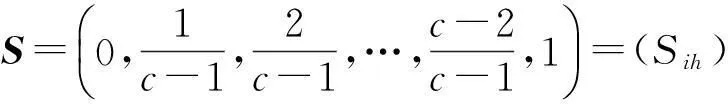
(2)

式中：c为级别总数；h=1，2，…，c。

建立目标函数，使全体方案对全部级别之间的加权广义欧氏距离平方和最小。

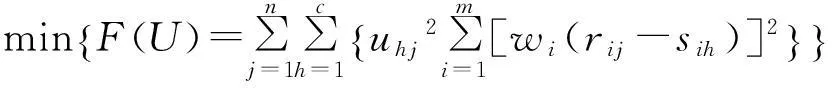
(3)

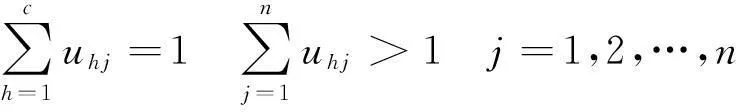
设满足约束条件可供选择的的n个方案X={X1,X2,…，Xn}组成方案集，设目标权向量为W=(w1,w2,…，wm)，则最优的目标权重应使决策者对偏见每个目标的所有二元对比权的偏差平方和最小。

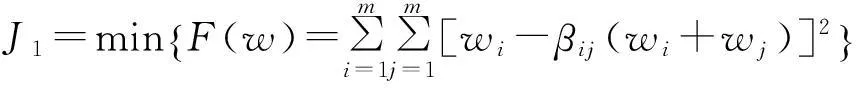
(4)

将主、客观权重综合考虑，建立权的偏差平方和最小的主客观权重综合模糊识别模型。

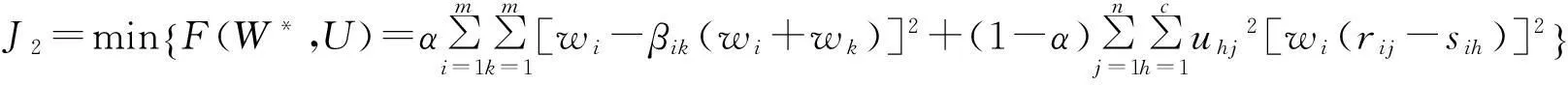
(5)

式中：α (0≤α≤1)为主观偏好影响系数，α越大，主观偏好影响力越大，反之，则影响力越小；rij为定量目标的规范化。

构造拉格朗日函数。

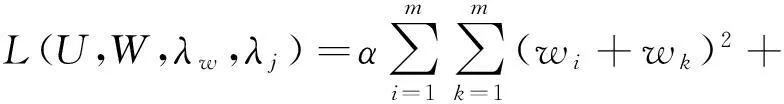
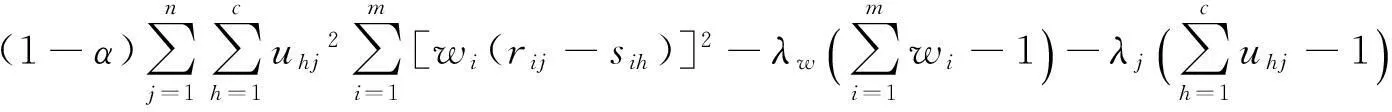
(6)

分别对w1，λw求导可得：

(8)

式中：

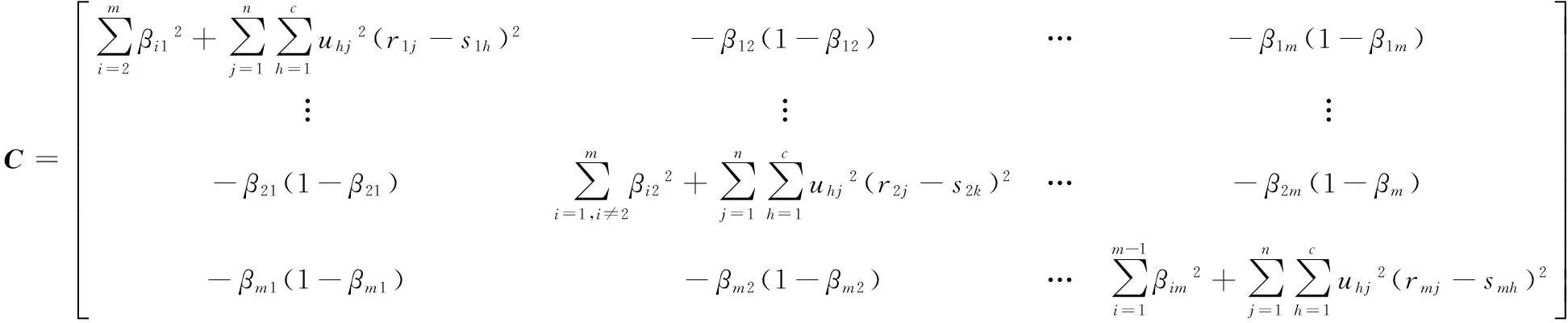
求解该模型，迭代结束即得到方案集对各个级别的相对隶属度。再根据级别特征值的向量式。

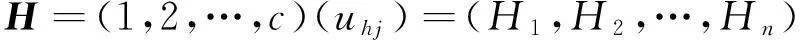
(9)

选取最大级别特征值即为最优方案。

2工程实例

某道路边坡位于低山地貌的丘陵地区，坡面倾向为东，坡度为28°。现状地形坡度较陡，表层主要由碎石性粘性土构成，其厚度为6.0～8.5m。路线以填方路堤形式为主，地基材料为粘性土中夹碎块石，结构较松散，空隙发育，透水性好，稳定性差，在K1+420～K1+540段，第四系堆积层厚度为27～32m．此路段路基在暴雨季节最小稳定性系数为0.82，具有滑动的可能性，为了保证路基的稳定，需对该段路基所处的边坡进行治理。

对于此段边坡提出4种治理方案：a1抗滑挡土墙，a2护面墙，a3喷混凝土，a4挂网喷浆。为确定较为合理的的边坡治理方案，经分析选择以下指标作为衡量方案优劣的标准，其中2个定量指标：工程造价，维护费用；4个定性指标：施工技术可行性与可靠性，处理效果，施工复杂程度，工程建设周期。

表2给出目标中定量的2个特征值。表3为综合评价指标。

表2　各方案定量指标特征值　元/m2

表3　综合分析评价指标

2.1　确定目标权重

对6个目标进行分析，就工程的重要性给出目标，根据二元比较排序标度矩阵。经判断可知该矩阵满足排序一致性条件，即为二元比较排序一致性标度矩阵。令ekl=1的元素，其二元比较模糊标度为βkl；ekl=0的元素，其模糊标度βkl=1-βlk；ekl=0.5的元素，其模糊标度βkl=0.5。由式(1)得有序模糊关系矩阵。

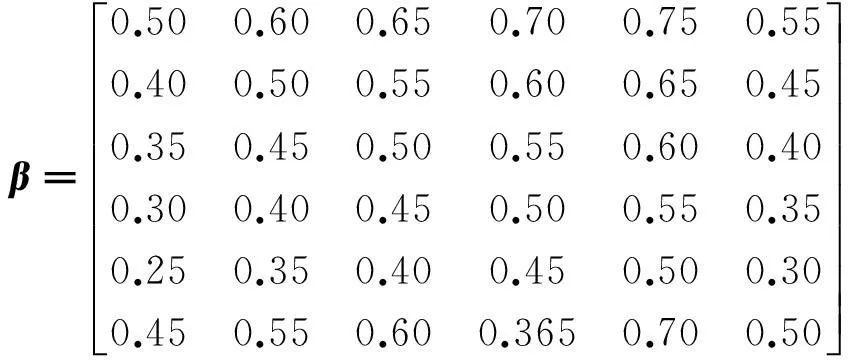
2.2　确定目标的相对隶属度

先确定目标③关于4个方案的目标相对优属度。通过比较，可得方案集就目标③的排序一致性矩阵，再次比较得方案就目标③的有序模糊关系矩阵。

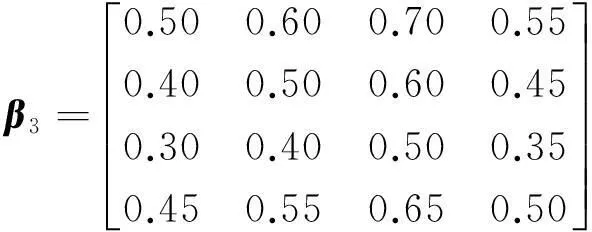
得目标③的优越性值：x3=(0.343 1,0.227 9,0.149 6,0.279 4)。

同理可得目标④的优越性值：x4=(0.166 4,0.342 8,0.270 3,0.220 5)。

目标⑤的优越性值：x5=(0.291 8,0.207 8,0.168 7,0.331 6)。

目标⑥的优越性值：x6=(0.339 6,0.184 0,0.204 0,0.272 4)。

对于成本性目标越小越好，归一化处理后可得方案目标相对隶属度矩阵。

2.3　确定方案集优劣的排序

取分级数c=2，由于方案间的比较仅在方案集X内进行，与X外的方案无关，再就差方案与优选的相对性，根据模糊优选的相对性，可定义理想方案与非理想方案为

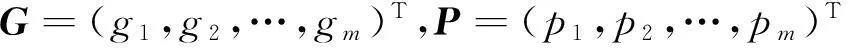
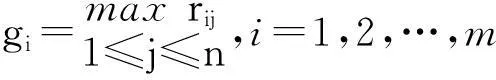
则由理想方案与负理想方案的目标特征值组成的目标标准特征值矩阵

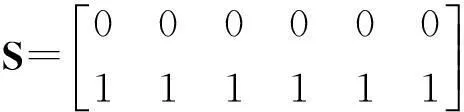
设W0= (1/6,1/6,…1/6)，由式(7)、(8)经过9次迭代，得到4个方案的相对隶属度矩阵，融合主、客观权重的指标权向量。

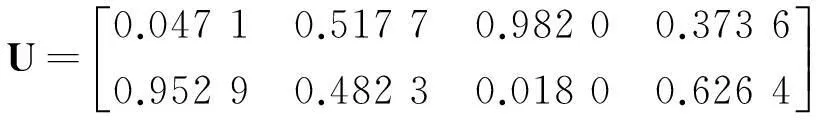
由模糊识别模型可得各目标的权重：W=(0.266 8，0.198 2，0.159 1，0.089 0，0.109 1，0.177 8)

由式(9)可得方案集的级别特征向量：H=(1.952 9,1.482 3,1.018 0,1.626 4)

则最优方案为a1，即抗滑挡土墙最为经济合理。

3结语

路基边坡防护工程主要涉及到工程的经济性、施工工期、治理效果等几个方面，本文通过建立治理方案决策的主、客观权重的综合模糊识别模型，有效组合主、客观权重，能在不同情况下得到较为客观系统的优化决策效果，避免了决策或评价的主观随意性，减少了目标的客观权重与实际情况的误差，较易体现专家的意见且符合工程实际情况。该模型适应性较强，计算量少，对其他综合评价也有一定的借鉴意义。

参考文献

[1]陈守煜.工程模糊集理论与应用[M].北京：国防工业出版社，1998.

[2]叶万军.多目标模糊识别优化决策理论与应用研究[D].大连：大连理工大学，2006.

[3]张哲.桥梁方案多层次多目标模糊优选模型及其应用[J].哈尔滨工业大学学报,2006(9):1567-1571.

[4]傅鹤林,彭思田.岩土工程数值分析新方法[M].长沙：中南大学出版社,2005.

[5]陈守煜.水资源与防洪系统可变模糊理论与方法[M].大连：大连理工大学出版社，2005.

收稿日期：2015-09-06

DOI 10.3963/j.issn.1671-7570.2015.06.025