改进型预测电流控制算法

李春鹏，贲洪奇，孙绍华，3，刘博

（1.哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨 150001;2.黑龙江省教育学院，黑龙江哈尔滨 150080;3.青岛科技大学自动化与电子工程学院，山东青岛 266000）

改进型预测电流控制算法

李春鹏1，2，贲洪奇1，孙绍华1，3，刘博1

（1.哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨 150001;2.黑龙江省教育学院，黑龙江哈尔滨 150080;3.青岛科技大学自动化与电子工程学院，山东青岛 266000）

为解决传统预测电流控制算法在并网逆变器电感参数失配时容易出现系统不稳定的问题，利用根轨迹法找出电感参数失配影响控制算法稳定性的原因。在此基础上提出一种改进型预测电流控制算法，通过对电流误差控制目标的修改和对逆变器理想输出电压的线性预测，在运算过程中不仅避免了预测程度的加深，还能减小电流环特征方程的各项权重系数，利用零极点对消改造电流环反馈系统的极点，使其特征方程的阶次始终为二阶。该算法在电感参数发生较大失配时，仍能保持系统稳定，使输出电流跟随给定。仿真和实验结果证明了所提算法的正确性和可行性。

三相并网逆变器;预测电流控制;电感参数失配;稳定性

0 引言

随着电力电子器件高频化和数字信号处理技术的日趋完善，目前三相电压型并网逆变器几乎都采用数字化控制，但由A/D转换时间、计算时间和零阶保持器等造成的控制延时问题会影响系统的稳定范围，在控制中不容忽视［1－2］。

预测电流控制因其具有超前一拍的控制特性，可用于消除控制延时造成的不利影响，但这种方法本质上是一种基于精确数学模型的控制算法，其控制效果依赖于并网逆变器模型参数的准确性，尤其对滤波电感的准确性要求较高［3－6］。而在实际应用中，由于测量误差以及系统运行条件的变化，滤波器电感值并不是恒定的，当电感实际值与标称值间存在较大偏差时，若按照预先确定的数学模型进行控制，输出电流将会发生畸变，严重时会使系统不稳定［7－9］。

为此，文献［10］对电流误差为零的传统预测电流控制算法进行了研究，采用0阶等距节点插值法对理想输出电压进行线性预估时，电感参数失配度（电感标称值与实际值之比）为1.25;采用1阶等距节点插值法时，电感参数失配度为1.08，此时实际电感若有轻微变化，极易导致系统不稳定。文献［11］提出了一种新的控制算法，令k+1时刻的电流误差等于前2个采样周期电流误差差分的一半，这种算法放宽了电流误差的控制目标并改变了理想输出电压的线性预测条件，降低了闭环脉冲传递函数的各项权重系数，可使电感参数失配度达到1.52。文献［12］不仅使系统具有较好的控制性能，还将电感参数失配度提高到2。文献［13］将电流误差设定为一个变值，根据系统特征方程的根必在单位圆内，求解出变值的取值范围，从中筛选出满足稳定条件的实数解，该算法通过减少预测过程中近似计算变量的个数和预测深度，将电感参数失配度提高到2.8。

通过对不同控制目标预测电流控制算法的比较分析，揭示电感参数失配影响控制算法稳定性的原因。在文献［11］的基础上，提出一种改进型预测电流控制算法。利用特定的k+1时刻电流误差以及对理想输出电压的线性预估，减少对中间变量的近似计算，降低算法的复杂程度。这种算法不仅能大幅提高电感参数的失配度，而且还具有较高的可靠性。仿真和实验结果证明了所提方法的正确性和可行性。

1 传统预测电流控制算法

1.1 基本原理

图1为三相电压型并网逆变器的拓扑结构，逆变器通过滤波电感L、线路等效电阻R与电网相连。

图1 三相电压型并网逆变器拓扑结构Fig.1Three-phase voltage grid-connected inverter topology

并网逆变器在αβ坐标系下的动态方程［14］为

式中:iα、iβ、να、νβ、ugα、ugβ分别为逆变器输出电流、输出电压和电网电压在αβ坐标系下的分量。

由于式（1）中没有耦合项且表述一致，因此可将下标略去，下面推导出的公式，对于αβ坐标系下的各轴分量是相同的。

对式（1）进行离散化处理，并忽略等效电阻R的影响，可得

式中:V（k）和Ug（k）分别为采样周期［k，k+1］内逆变器平均输出电压和电网平均电压;i（k+1）为k+1时刻的电流瞬时值;i（k）为k时刻的电流瞬时值。

令逆变器的理想输出电流为i*，则式（2）可写为

式中:V*（k）为采样周期［k，k+1］内逆变器理想输出电压。

将式（2）和式（3）相减，可以得到

式中:ie（k+1）=i*（k+1）－i（k+1）为k+1时刻的电流误差。

在式（4）中，若想得到V（k），需对V*（k）进行预估，并且要设定k+1时刻的电流误差ie（k+1）。对于k+1时刻电流误差的设定可分为2种:一种是令k+1时刻的电流误差为零［11］;另一种是令电流误差不为零，而是与前k个采样周期的电流误差结果有关［12］。

1.2 电流误差为零的控制算法

将ie（k+1）=0代入式（4），可以得到

由于采用定频调制，故采样周期相等，因此对V*（k）的预测可用0阶或1阶等距节点插值来近似。

观察式（9）和式（11）发现，在消除ie（k）的过程中，随着对V*（k）预测程度的加深，式（11）中所包含的V（k）和ie（k）历史值数量及其权重值都有所增加，表明式（11）的平均输出电压对这些项的依赖性在增加。

1.3 电流误差不为零的控制算法

将ie（k+1）改为前两个采样周期电流误差差分

注意式（9）中的ie（k）项，本应在第［k－1，k］采样周结束时就能得到，但由于数字控制与采样间的时序关系，却要等到下一采样周期结束时才能获得，因此在使用中必须消掉ie（k）项。为此，需要对理想输出电压做进一步预测为的一半，即

根据上文的推导过程，可以得到

如果令式（11）的λ=0.5，则式（14）与式（11）相比，它们所包含的V（k）和ie（k）历史值数量相同，只是式（14）中对应项的权重值相对较小，表明式（14）的平均输出电压对这些项的依赖性在减小。

2 电感参数失配对预测算法稳定性的影响

式中，L为电感实际值。

将式（9）、式（11）和式（14）中的L写成Ln，并分别代入式（15）中，对其传递函数进行z变换，构成闭环反馈系统。图2是由预测电流控制算法构成的闭环反馈控制系统框图。其中i*（k）和i（k）分别为电流环的输入量和输出量，并网电压Ug（k）相当于一个扰动量，在证明电流环的稳定性时可不用考虑。

利用式（2）可以得到k+1时刻的实际电流

根据图2可以得到由式（9）和式（15）构成的闭环脉冲传递函数为

式中:m=Ln/L为电感参数失配度;Ln为电感标称值。

令z=（ω+1）/（ω－1）并代入式（16）的特征方程中，可得

由式（18）～式（20）可绘出式（16）稳定条件下m与λ之间的关系如图3（a）所示。图中填充部分为m的取值范围，从中可以看出，随着λ的增加，m的取值范围先增大后减小，最后在式（20）和式（18）之间变化，其中λ=0.5时，m的最大值为2。所以在对理想输出电压V*（k）进行预测时，λ的最佳取值范围在［0，0.5］之间。

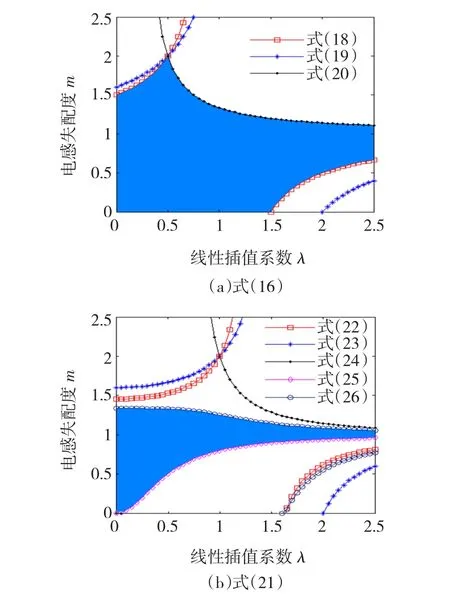
图3 电感失配度m与线性插值系数λ间的关系图Fig.3The relationship figure between m and λ

由式（11）和式（15）构成的闭环脉冲传递函数为

图3（b）为式（21）中m与λ之间的关系，其中m的取值范围明显比图3（a）中的取值范围要小，只能在式（26）和式（25）之间变化，且随着λ的增加，m的取值范围逐渐变窄。

由式（14）和式（15）构成的闭环脉冲传递函数为

图4和图5分别是λ取不同值时式（16）和式（21）的根轨迹。从中可以看出，随着式（16）和式（21）中λ值的增加，不仅增大了各算法闭环脉冲传递函数的各项权重系数，而且还提高了系统特征方程的阶次，导致m的取值范围逐渐下降。而当λ值相同时，式（21）特征方程的阶次要比式（16）的阶次高出一阶，其对应项的权重系数也相应增大，使得m的取值范围也明显下降。

图4 不同λ值时，式（16）的根轨迹图Fig.4Different λ，（16）the root locus diagram

图5 不同λ值时，式（21）的根轨迹图Fig.5Different λ，（21）the root locus diagram

图6为式（27）的根轨迹图。当放宽k+1时刻电流误差ie（k+1）的控制目标和改变V*（k）的线性预测条件后（令λ=0.5），降低了闭环脉冲传递函数的各项权重系数，大幅提升了算法对电感参数失配的容忍度。即使m=1.52时，仍然能保持系统稳定。

图6 式（27）的根轨迹图Fig.6（27）The root locus diagram

通过以上对传统预测电流控制算法稳定性的分析，若想提高系统m的取值范围，必须要做到:1）降低系统闭环特征方程的阶次;2）减小平均输出电压中的各项权重系数，λ的取值要小，可在［0，0.5］范围内选取，即降低算法对前k个采样周期结果的依赖性;3）在消除ie（k）项的过程中，应尽量减少对理想电压V*（k）的预估次数，避免预测程度的加深。

3 改进型预测电流控制算法

3.1 改进型预测电流控制算法的构成

根据第2节的结论，提出一种改进型预测电流控制算法。将k+1时刻的电流误差设计为

为了减少对理想电压V*（k）的预估次数，必须消掉ie（k）项，故令其系数为零，可求出x=λ+1。此时，式（31）可以表示为

在构建式（32）的过程中，因为只对V*（k）进行了一次预估，所以避免了预测程度的加深。

将式（32）代入式（15）中，可得开环脉冲传递函数

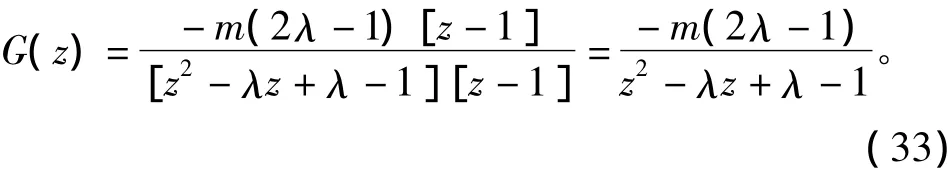
由于式（33）中的零极点可对消，因此，该算法可将系统的阶数控制在二阶，降低了算法的复杂度。

3.2 改进型预测电流控制算法的稳定性分析

由式（32）和式（15）构成的闭环脉冲传递函数为

对式（34）的特征方程进行ω变换，得到关于ω的一元二次方程为

λ的大小直接影响算法对电感参数失配的容忍度，而式（36）中确定的λ取值范围明显减小了式（34）中的各项权重系数，因此降低了算法对各项权重系数的依赖程度。图7为改进算法中m与λ之间的关系，其中m的取值范围随着λ的增加而逐渐变宽。通过与图3的比较可知，该方法明显提高了m的取值范围。

图7 式（34）电感失配度m与线性插值系数λ间的关系图Fig.7（34）The relationship figure between m and λ

图8为λ=1/4时式（34）的根轨迹。由图可知，当0＜m＜3.5时，算法仍能保持稳定。综上所述，改进型预测电流控制算法不仅保留了式（14）的优势，而且还提高了算法对电感参数失配的容忍度，从而使闭环系统的稳定性得到大幅提升。

4 仿真与实验研究

4.1 预测算法仿真

为验证改进算法的有效性和控制性能，采用Matlab对其进行仿真。仿真参数:直流母线电压Udc= 400 V，标称电感Ln=6.4 mH，开关频率为8 kHz;电网相电压为110 V。

图9是m=1时采用式（11）和式（32）得到的并网逆变器a相电流波形及其频谱。此时两种电流预测控制算法的控制效果差别较小，a相电流波形都是正弦波，且谐波含量均比较低。

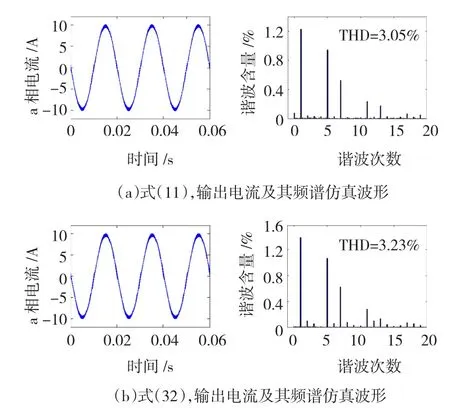
图9 m=1时，逆变器输出电流及其频谱仿真波形Fig.9m=1，Simulation waveforms of output current and spectrum of the inverter

图10为m=0.8时的情况，采用式（32）得到的a相电流波形与m=1时相比未发生较大变化，THD变化不大;而采用式（11）得到的a相电流波形已发生畸变，THD显著增加。图11为m=1.2的情况，通过观察其电流波形和频谱，可以得到与图10相似的结论。

图10 m=0.8时，逆变器输出电频谱仿真波形Fig.10m=0.8，Simulation waveforms of output current and spectrum of the inverter

图11 m=1.2时，逆变器输出电流及其频谱仿真波形Fig.11m=1.2，Simulation waveforms of output current and spectrum of the inverter

4.2 实验研究

为了验证新算法的有效性，以TI公司的TMS320F2812为核心控制器，设计了一台额定功率为2.3 kW的三相并网逆变器原理样机。

对式（11）和式（32）两种预测控制算法进行实验比较。从图12可以看出，当m=1时，两种算法的控制效果差别不大，系统都能稳定运行，而且a相电流谐波含量较低，采用式（11）时其THD=3.3%，采用式（32）时其THD=3.5%。

当m=0.8和m=1.2时，采用两种控制算法得到的逆变器a相电流波形及频谱分别如图13和图14所示。由图13和图14可知，采用式（11）得到的逆变器a相电流还能维持稳定，但电流波形发生畸变，THD明显升高;而采用式（32）时，电流波形未发生太大变化，其THD变化较小。

图12 m=1时，逆变器输出电流及其频谱Fig.12m=1，Output current and spectrum of the inverter

图13 m=0.8时，逆变器输出电流及其频谱Fig.13m=0.8，Output current and spectrum of the inverter

当m=1.5时，传统算法已进入不稳定工作状态，而改进算法仍能保持稳定工作。图15为采用式（32）得到的逆变器a相电流波形及频谱，可以看出，电流波形为正弦波，只是谐波含量有所上升。

图14 m=1.2时，逆变器输出电流及其频谱Fig.14m=1.2，Output current and spectrum of the inverter

图15 m=1.5时，逆变器输出电流及其频谱Fig.15m=1.5，Output current and spectrum of the inverter

5 结论

本文着重分析了传统预测电流控制算法稳定性与电感参数失配的关系，总结出电感参数失配影响控制算法稳定性的原因。通过对电流误差以及逆变器理想输出电压构建形式的修改，提出一种改进型预测电流控制算法。该方法保留了传统预测电流控制算法的优势，不仅能增强算法的稳定性，还能减少对理想输出电压的预估次数，通过零极点对消，将系统保持在二阶。最后，对传统算法和改进算法进行了仿真分析与实验比较，结果表明，随着电感参数失配度的加深，传统算法控制下的相电流波形发生明显畸变，谐波含量显著增加，最终进入不稳定状态;而改进算法仍能保证系统稳定，使并网电流跟随给定，相电流谐波含量变化相对较小。由此证明所提出方法的正确性和可行性。

［1］刘剑，杨贵杰，高宏伟，等.双三相永磁同步发电机的矢量控制与数字实现［J］.电机与控制学报，2013，17（4）:50－56，63.

LIU Jian，YANG Guijie，GAO Hongwei，et al.Vector control for dual three－phase PMSG and digital implementation［J］.Electric Machines and Control，2013，17（4）:50－56，63.

［2］周雒维，孙鹏菊，杜雄.数字控制DC－DC变换器的延时离散模型及影响分析［J］.电机与控制学报，2010，14（5）:7－12.

ZHOU Luowei，SUN Pengju，DU Xiong.Discrete－time modeling of digital controlled DC－DC converters and the effects of time delay［J］.Electric Machines and Control，2010，14（5）:7－12.

［3］王伟华，肖曦.基于电感辨识的PMSM电流自适应增量预测控制［J］.电机与控制学报，2014，18（2）:75－82.

WANG Weihua，XIAO Xi.Adaptive incremental predictive control method for current of PMSM based on online identification of inductance［J］.Electric Machines and Control，2014，18（2）:75－82.

［4］ABU－RUB H，GUZINSKI J，KRZEMINSKI Z，et al.Predictive current control of voltage－source inverters［J］.IEEE Transactions on Industrial Electronics，2004，51（3）:585－593.

［5］MOHAMED Y，EI－SAADANY E.Robust high bandwidth discrete－time predictive current control with predictive internal model－a unified approach for voltage－source PWM converters［J］.IEEE Transactions on Power Electronics，2008，23（1）:126－136.

［6］ESPI H J，CASTELLO M J，FISCHER J R，et al.A synchronous reference frame robust predictive current control for three－phase grid－connected inverters［J］.IEEE Transactions on Industrial E-lectronics，2010，57（3）:954－962.

［7］RODRIGUEZ J，PONTT J，SILVA C A，et al.Predictive current control of a voltage source inverter［J］.IEEE Transactions on Industrial Electronics，2007，54（1）:495－503.

［8］CHIH C H，CHUN W W，CHIH W C.A digital predictive current control with improved sampled inductor current for cascaded inverters［J］.IEEE Transactions on Industrial Electronics，2009，56 （5）:1718－1726.

［9］FANG Yu，XING Yan.Design and analysis of three－phase reversible high－power－factor correction based on predictive current controller［J］.IEEE Transactions on Industrial Electronics，2008，55（12）:4391－4397.

［10］HOLMES D G，MARTIN D A.Implementation of a direct digital predictive current controller for single and three phase voltage source inverters［C］//31th IEEE Industry Applications Conference，October 6－10，1996，San Diego，CANADA.1996:906－913.

［11］BODE G H，POH C L，NEWMAN M J，et al.An improved robust predictive current regulation algorithm［J］.IEEE Transactions on Industry Applications，2005，41（6）:1720－1733.

［12］KOJABADI H M，BIN Y，GADOURA I A，et al.A novel DSP－based current－controlled PWM strategy for single phase grid connected inverters［J］.IEEE Transactions on Power Electronics，2006，21（4）:985－993.

［13］于蓉蓉，魏学业，吴小进，等.一种改进型预测电流控制算法［J］.电工技术学报，2010，25（7）:100－107.

YU Rongrong，WEI Xueye，WU Xiaojin，et al.An improved predictive current control algorithm［J］.Transactions of China Electrotechnical Society，2010，25（7）:100－107.

［14］杨勇，索迹，祁春清，等.三相并网逆变器电感在线辨识控制［J］.电机与控制学报，2011，15（3）:52－57.

YANG Yong，SUO Ji，QI Chunqing，et al.Inductance online identification control for three－phase grid－connected inverters［J］.Electric Machines and Control，2011，15（3）:52－57.

（编辑:刘琳琳）

Research of improved predictive current control algorithm

LI Chun-peng1，2，BEN Hong-qi1，SUN Shao-hua1，3，LIU Bo1
（1.School of Electrical Engineering and Automation，Harbin Institute of Technology，Harbin 150001，China;
2.Heilongjiang Province Education College，Harbin 150080，China;3.College of Automation and Electronic Engineering，Qingdao University of Science and Technology，Qingdao 266000，China）

In order to solve the traditional predictive current control algorithm in the grid inverter inductance parameter mismatch system prone to instability problems，Root-Locus method was used to find out the cause of the inductance parameter mismatch affecting the stability of the control algorithm.Then a modified predictive current control algorithm was put forward，based on the current deviation conditions of modification and the ideal output voltage linear prediction，the deepening degree of prediction was avoided，the weight coefficient of current loop characteristic equation was reduced，and pole zero cancellation was used to reform the current loop feedback control system pole，making the order of characteristic equation the second all the time.When the inductance parameters occurs worse mismatch，the algorithm still can maintain stability of the system，and make the output current follow the given.Simulation and experiment prove the correctness and feasibility of the algorithm.

three phase grid-connected inverter;predictive current control;inductance parameter mismatch;stability

10.15938/j.emc.2015.03.010

TM 464

A

1007－449X（2015）03－0061－08

2014－06－17

国家自然科学基金（51107017）

李春鹏（1976—），男，博士研究生，研究方向为并网逆变技术及其应用;

贲洪奇（1965—），男，博士，教授，博士生导师，研究方向为高频功率变换技术及有源功率因数校正技术;

孙绍华（1977—），女，博士研究生，研究方向为并网逆变技术及其应用;

刘博（1992—），男，硕士研究生，研究方向为并网逆变技术及其应用。

贲洪奇