风能转换系统随机建模与H∞容错控制

史运涛，侯彦娇，孙德辉，李正熙

（北方工业大学现场总线技术与自动化北京市重点实验室，北京 100144）

风能转换系统随机建模与H∞容错控制

史运涛，侯彦娇，孙德辉，李正熙

（北方工业大学现场总线技术与自动化北京市重点实验室，北京 100144）

针对带有传感器、执行器故障的风能转换系统（WECS）的建模与容错控制问题，提出了基于随机分段仿射（PWA）模型的建模方法和H∞容错控制方法。建立了风电机组多工作区域的随机PWA正常模型;针对WECS的桨距角传感器故障、功率测量传感器故障、桨距角执行器故障、电机电磁转矩执行器故障，建立风能转换系统的随机PWA故障模型;基于WECS系统的正常和故障的随机PWA模型，利用非线性耗散系统的稳定性理论与H∞鲁棒控制方法，提出并证明了WECS系统的H∞容错控制器存在性定理，给出控制器求解方法。仿真结果表明本文所提出的基于随机PWA模型的风能转换系统的H∞容错控制方法对于存在的传感器、执行器增益故障具有较好的容错控制性能。

容错控制;随机PWA;风能转换系统;H∞控制

0 引言

风能作为重要的清洁能源，得到世界各国的重视。风能转换系统是由风轮叶片系统、齿轮箱主传动链系统、发电机系统以及其控制系统组成，是典型的机、电、液一体的复杂的非线性动力学系统，在随机、间歇性的风力作用下表现出随机、切换的特性。对于这样的系统实现建模与控制是一个比较困难的问题;同时，风力发电机组的控制系统中存在传感器、执行器等常见故障［1-2］，控制系统的故障严重的影响风力发电机组的性能与安全。因此，风能转换系统的容错控制技术的研究对于风电机组的安全、高效运行具有非常重要的意义。

近年来，国内外已经开始了对于风力发电系统的容错控制研究［2-9］:在文献［6］中，Sloth等人利用线性变参数（LPV）控制器设计方法设计了风电机组的主动和被动容错控制器;在文献［7］中，作者提出了双馈式感应发电机的基于模型的故障检测和控制回路重组的主动容错方法;文献［8］给出了直驱式风力发电机变流器的容错控制方法;在文献［9］中，作者设计了一种针对变桨距控制系统的容错开关磁阻电机。目前对于风力发电机组的建模与容错控制的研究的主要缺点是没有深入描述风力发电机组的随机、非线性切换的动力学特性。一些研究者仅考虑非线性特性，利用滑模变结构、反馈线性化等技术手段设计非线性控制器，但是系统建模中没有考虑其随机与切换特性。就作者所知，还没有在随机、非线性动力学建模框架下，针对风能转换系统的传感器与执行器故障的容错控制器设计方法的研究。

分段仿射系统是分析和设计非线性系统的强有力工具，很多非线性系统可以用PWA系统以任意精度进行逼近，PWA系统还与几类典型的混杂系统（如混合逻辑动态系统、线性混合自动机等）等价;随机的PWA模型则是在PWA模型的基础上考虑了系统受到随机信号的干扰作用下的情况，是对于PWA模型的一个特别有意义的扩展，从而大大的增强其随机建模的能力。目前在保证随机PWA系统稳定和H∞控制方面已经取得一系列的成果［11-15］。Cuzzola在文献［15］中讨论了离散PWA系统H∞控制器设计方法，但结论只适用于没有仿射项的系统;随后Feng和Xu分别在文献［10］、［16］中重新给出结论适合于具有仿射项的系统的离散PWA的H∞控制器的设计方法。

本文利用随机PWA模型，将非高斯的风力信号（符合威布尔分布）转化为湍流信号与一个平均风速的叠加，从而把风速信号进行分解:低频部分（平均风速）转化为PWA模型的位移常数项（displacement），高频部分（湍流部分）表示为普通高斯信号经过（与该点平均风速相关）二阶成型滤波器，据此建立了风电机组多工作区域的随机PWA模型，针对WECS的传感器故障（桨距角传感器故障、功率测量传感器故障）和执行器故障（桨距角执行器故障、电机电磁转矩执行器故障）建立风能转换系统的随机PWA故障模型;在随机PWA模型框架下，推导并证明了H∞容错控制器存在条件和设计方法。本文由以下几部分组成:第1部分简单描述了WECS的随机、非线性动态模型和切换控制策略; WECS的随机PWA故障建模方法在第2部分中做了介绍;针对WECS的传感器故障、执行器故障的H∞容错控制方法在第3部分中展开讨论;仿真结果和相关分析在第4部分给出;最后给出结论部分。

1 WECS的动态模型和控制策略

WECS（图1）的输入为风速v（t），桨距角设定值βref（t）和电磁转矩设定值Tgref（t），系统的输出为发电机功率Pg（t）和高速轴转速ωg（t）。

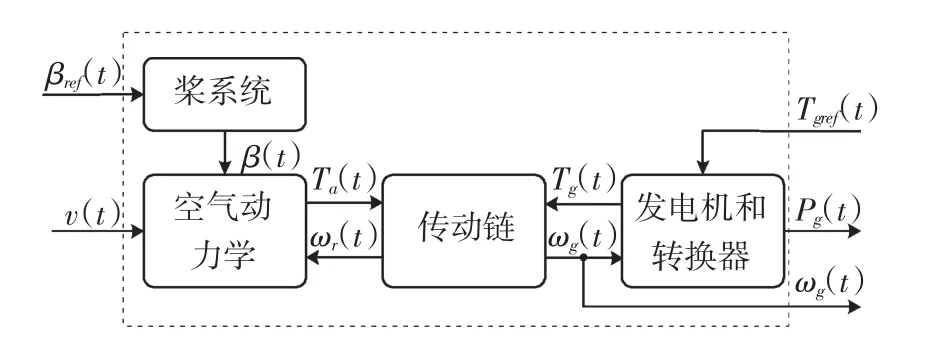
图1 WECS的结构图Fig.1The structure of WECS

1.1 风模型

风由两部分叠加产生［13］，如式（1）所示，vm（t）是低频部分（描述长期，低频变化量），代表平均风速;vs（t）是湍流部分（对应于快速，高频变化量）。

1.2 空气动力学模型

穿过整个风轮旋转平面面积的风的有效功率表示为:

式中:A为风轮旋转平面面积，Pw为风的有效功率，v为风轮采集到的有效风速，ρ为空气密度，被考虑为常量。基于风的有效功率，风轮捕获功率可根据功率系数Cp（λ，β）得出，功率系数的大小依赖于叶尖速比λ和桨距角β。风轮捕获功率为:

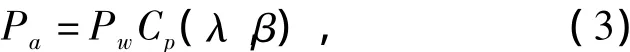
式中:Pa为转子捕获功率。

叶尖速比定义为叶尖速度和风轮有效风速的比值:

式中:ωr是低速轴转速。

1.3 传动链模型

传动链是传递风能的主要装置，由低速轴、高速轴、齿轮以及弹性装置组成。传动链动态方程如下:

式中:Jr和Jg分别为低速轴和高速轴的转动惯量，Ks是传动链的弹性装置的刚性系数，Ds为传动链的弹性装置的阻尼系数，Ng为齿轮比，δ为柔性传动链的扭转度

1.4 桨距系统模型

变桨距控制系统可以由一个二阶模型来表示［14］，其状态方程为:

1.5 发电机和变流器模型

就整体而言，风力发电机与整流器模型可以用一阶模型代替，即电磁子系统:

式中:τg为时间常数。时发功率可描述为:

综上，由各个部分的模型可以得到整个风电机组的完整模型:

1.6 控制策略

风电机组的控制策略如图2所示。

图2 风电机组的控制策略Fig.2The control strategy for wind turbine

风电系统在不同的风速时对功率和转速均有不同的控制要求，一般来说在风速达不到系统切入风速时，风机不启动;在风速未达到额定风速前，风机需最大效率的捕获风能;当风速超过额定风速则需要限制功率上升并保持系统稳定。

如图3在A—B段即切入风速前，系统处于停机状态;

图3 β、Tg和Pg随风速的变化趋势Fig.3The tendency of the β、Tgand Pgfollowing the wind speed

在B-C段又称部分负荷段，控制的主要目标在于功率的最大捕获。通过调节桨距角和电磁转矩使得功率系数Cp（λ，β）获得最大值，当风速继续增大时，应注意控制高速轴转速ωg的值不要超过电机的阈值转速。

在C—D段又称满负荷段，此时的控制目标是保持时发功率Pg维持在额定值Pgnom，同时限制高速轴转速ωg维持在［ωgnomωgmax］之间。变桨控制的主要目的则变为限制风能的捕获即限制功率，避免增加系统的机械负荷。

在D—E段接近切出风速后，改变桨距角的值以尽量减少风能的捕获。同时系统与电网断开，抱闸停机。

2 WECS在随机PWA框架下的故障建模

综上所述，风电系统主要工作在四个工作区间，本节首先介绍随机PWA建模方法，然后给出了风电系统的随机PWA建模过程:

2.1 随机PWA模型框架

离散时间随机PWA系统的状态空间方程如下所示:

式中:xk∈ RRn为系统状态，uk∈ RRm为控制输入，zk∈R Rm是一个可建模的性能输出，所有可能的向量的集合⊆ RRn+m既可以是n+m维的实空间 RRn+m，也可以是包含原点的多面体，{χi}si=1是的一个多面体划分，ai∈ RRn是常数向量。

把每一个χi当作一个单元，假定每一个单元都是多面体形式的，由矩阵定义为如下形式:

Sj:={所有的i，∃x，u和x∈，xTu [T]T∈

2.2 WECS的随机PWA模型

某一静态工作点，可以利用泰勒级数展开的方法实现非线性动力学特性的线性化展开的方法，将χi}。用I={1，…，s}代表所有χ下标i可能满足的集合，同时J={1，…，t}代表所有下标j可能满足的集合;同时必须满足传动链模型进行线性化，线性化后的传动链动态方程如下所示:

由此，可以得到一个线性化的WECS整体动态状态空间模型:

随机的风力载荷提供驱动风机的能量，可以看为平均风速vm和随机部分vs的叠加，平均风速可以是一个常量。根据文献［15-16］，高频湍流部分vs可以看作是白噪声经过二阶滤波器之后的“点风”，二阶滤波器模拟了由风轮叶片扫过的盘状区域的影响。在频域中，vs的功率谱密度Svs可以写为Svs（f，vm）=Sp（f）Sf（f，vm），式中:Sp（f）是“点风”的频谱，Sf（f，vm）代表基于平均风速的滤波器。然后风速模型的湍流部分表示成白噪声过程近似为一个线性二阶传递函数:

式中:ω1=vs，e∈N（0，1），a1、a2、a3为基于平均风速的参数。

则式（12）中的模型可以转化成如下形式:

根据图4，选择3个工作点，风机本身的参数如转动惯量等可直接得到，各个工作点的的值通常由一个有效的风力估计器根据不同的风速求取［17-18］。

图4 风速和相对应的工作点Fig.4Wind speed vs.the corresponding working point

其中，风力发电机组的模型参数为:低速轴转动惯量Jr=90 000 kg·m2，高速轴转动惯量Jg=10 kg·m2;传动链的弹性装置的刚性系数Ks=8×106N·m/rad，传动链的弹性装置的阻尼系数Ds=8×104kg·m2/ （rad·s）;时间常数τβ=0.15 s，τg=0.1 s;时发电功率额定值Pg，nom=225 kw;低速轴转速额定值ωr，nom=4.29 rad/s，高速轴转速额定值ωg，nom=105.534 rad/s，低速轴转速最低值ωr，min=3.5 rad/s，高速轴转速最低值ωg，min=86.1 rad/s。其中，风力发电机组不同工作点的线性模型参数如表1所示。

表1 不同工作点的线性模型参数Table 1Parameters of linearized model in different working points

2.3 WECS的执行器故障和传感器故障模型

在本文的工作中，同时考虑执行器故障和传感器故障。用uj表示第j个执行器或传感器，uFj表示第j个失效的执行器或第j个失效的传感器。将执行器或者传感器中的一种增益丢失表示为:

式中:αj表示第j个执行器或传感器的失效比，αMj是对应的最大失效比，αj=0表示对应的执行器或传感器没有失效，0＜αj＜1表示对应的执行器或传感器部分失效;αj=1表示对应的执行器或传感器完全失效。定义α=diag{α1，α2，…，αm}，则uF= Γu，其中Γ=（1-α）。文中考虑的故障如表2所示。

表2 文中考虑的故障Table 2The considered faults

其中Γa和Γs均为二阶对角矩阵。

带有执行器增益丢失Γa的WECS系统的随机PWA模型如下所示:

同理，带有传感器增益丢失Γs的WECS系统的随机的PWA模型如下所示:

3 风能转换系统的H∞容错控制

3.1 执行器故障容错控制

根据执行器故障的PWA模型（16），将输入干扰信号wk扩展为:

本文考虑的H∞框架是基于l2有限时域定义的，因此，对干扰输入的扩展是合理的。

由此文献［5］中提到的控制方法可以直接应用到扩展系统（19）。在标准的假设下:

通过这种方式，控制器可以考虑到如下置换ai=D，其中D=[0I]。

通过将控制律（22）应用到PWA系统（19），可以得到闭环PWA执行器故障系统:

则系统（23）满足（25）式所示的耗散不等式，同时，系统（23）是PWQ稳定的。

证明回忆初始条件x0=0，则式（25）有如下的关系式，∀N≥0

明显的，如果条件（26）成立，那么不等式（29）也成立。另外，认为Cij≥0，所以由式（26）的元素（1，1），可以得到

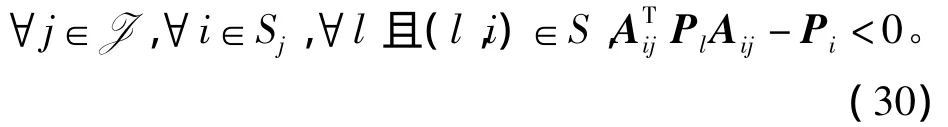
此式表明系统（23）是PWQ稳定的。

以下针对（16）式所描述的WECS系统中存在执行器增益故障，寻找一种形如（22）式的状态反馈H∞控制律实现系统被动容错控制，主要结果可归纳为如下的定理:

定理1对于PWA系统（16），存在一个形如（22）的状态反馈控制律能够保证系统PWQ李雅普诺夫稳定并满足如下供应率:可以得到状态反馈矩阵K1j（j∈J）为:

证明通过引用舒尔引理，可以将式（26）改写为:

明显看出，对于Qi＞0，∀i∈I，控制矩阵可以重写为式（33）的形式。

3.2 传感器故障容错控制

定理2对于PWA系统（17），存在一个形如（22）的状态反馈控制律能够保证系统PWQ李雅普诺夫稳定并满足供应率为

4 仿真结果与分析

本文在平均风速为7.5、10、16 m/s3个工作点建立了WECS系统的随机PWA模型，并设计了WECS系统正常情况下的H∞状态反馈控制器;建立了WECS系统桨距执行器及发电机执行器的PWA故障模型（故障因数Γa=0.6），根据定理1设计了执行器故障下的H∞容错控制器;建立了WECS系统电机转速传感器及电机功率传感器故障的随机PWA模型（故障因数Γs=1.2），根据定理2设计了传感器故障下的H∞容错控制器;以下给出了WECS系统在三个工作点的随机PWA模型，并给出了根据定理1和定理2计算的状态反馈系数矩阵;分别在4.1、4.2、4.3节中给出了WECS系统正常、执行器故障和传感器故障三种情况下的仿真结果。

根据第2部分的建模过程，可以得到WECS的如下随机PWA模型:

如果0＜E1xk≤8，有

状态空间分割矩阵:E1=［0 0 0 0 0 1 0］。

根据本文所推导的定理1和定理2可以成功求解WECS系统在正常、传感器故障、执行器故障情况下的分段线性状态反馈矩阵K1，K2，K3，保证WECS系统满足PWQ李亚普诺夫稳定。三种情况下求取的反馈矩阵如下:

WECS系统正常时反馈增益矩阵为

4.1 正常WECS系统的H∞控制仿真结果

在仿真中，利用式（9）所描述的WECS系统的非线性模型作为实际的被控对象。图5给出了无故障的WECS系统在本文所设计的H∞控制器作用下的动态响应结果。图5（a）给出了用于测试的风速信号，其平均风速vm分别取值7.5、10、16m/s，在100、200、300s进行切换;图5（b）给出了WECS系统在H∞控制器作用下的叶尖速比曲线，图5（c）则给出了最大功率点跟踪算法（MPPT）计算出的最优发电功率设定值的曲线;图5（d）和图5（e）给出了发电机转速和实时功率的响应曲线，从图中可以看出实时功率较好的跟踪了功率设定值，发电机转速控制性能良好;图5（f）和图5（g）给出了控制器输出的桨距角和发电机转矩的曲线;图5的仿真结果表明:本文所设计的WECS系统基于随机PWA模型的H∞控制器取得较好的控制效果。

图5 风电机组基于随机PWA模型的H∞可靠容错控制仿真结果Fig.5Simulation results of H∞reliable control for normal WECS based on stochastic PWA model

4.2 带有执行器故障的WECS模型的H∞控制仿真结果

图6 风电机组存在执行器故障但无容错控制的仿真结果Fig.6Simulation results of actuators fault of WECS without fault tolerant control

图6和图7给出了风电系统存在桨距系统执行器故障增益损耗Γβ及发电机执行器故障增益ΓTg状态下（本文中令增益损耗Γβ=ΓTg=0.6）的仿真结果;图6给出了风力发电系统在存在两个执行器故障，无容错控制器作用下的响应曲线。图7给出了根据定理1设计的执行器故障容错控制器作用下的控制效果。图6（a），（b），（c）曲线与图5（a），（b），（c）相比较，曲线变化很小，说明MPPT算法在传感器故障下也能很好的工作。另一方面，相对于图5的（d）和（e）曲线，图6中的（d）发电机功率Pg和（e）发电机速度ωg的性能恶化，并开始展现出失去稳定的趋势。图6（f）和6（g）中的控制变量显示出了大范围的振荡。由此可以看出，对于风能转换系统正常模型下的H∞控制器无法处理风能转换系统存在执行器增益因子损失的故障。和图6（d），（e）进行比较，图7 （d），（e）给出了执行器故障容错控制器作用下的WECS系统的发电机转速和发电机的功率的响应曲线。从图7中可以看出，存在容错控制器比没有容错设计的正常控制器的性能显著提高了，发电机功率Pg和发电机速度ωg保持稳定的趋势。

图7 风电机组存在执行器故障下的H∞可靠容错控制仿真结果Fig.7Simulation results of H∞fault tolerant control for actuators fault of WECS

4.3 带有传感器故障的WECS模型的H∞控制仿真结果

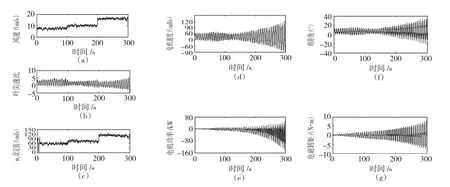
图8 风电机组存在传感器故障但无容错控制的仿真结果Fig.8Simulation results of sensors fault of WECS without fault tolerant control

图9 风电机组存在传感器故障下的H∞可靠容错控制仿真结果Fig.9Simulation results of H∞fault tolerant control for sensors fault of WECS

图7和图8给出了风电系统在存在电机速度传感器故障增益Γω及发电机功率传感器故障增益ΓP状态下（本文中令增益故障因数Γω=ΓP=1.2）的仿真结果;图8给出了风力发电系统在存在两个传感器故障，无容错控制器作用下的响应曲线。图9给出了根据定理2设计的传感器故障容错控制器作用下的控制效果。在图8（d），（e）中发电机功率和发电机转速的性能已经恶化，而且完全失去稳定，同时在图8 （f），（g）中的控制变量也显示出大范围的振荡;而图9（f），（g）表明在容错控制器的作用下，风能转换系统的输出获得了较好的性能，发电机功率很好的跟踪了MPPT算法的输出，发电机的转速响应速度快并且无任何静态误差，发电功率也能够跟踪功率的最优设定。

5 结论

本文针对具有传感器、执行器故障的风能转换系统的建模与容错控制问题，提出了一种随机PWA的建模方法解决了风能转换系统（WECS）正常与故障情况的建模问题;利用非线性耗散系统的稳定性理论与H∞容错控制方法，以定理形式给出了WECS系统在传感器与执行器故障情况下H∞容错控制器设计方法。实际的仿真结果表明本文所提出的随机PWA建模与H∞容错控制方法能够很好的解决随机风力载荷作用下的风能转换系统的建模与容错控制问题。

［1］ODGAARD P F，STOUSTRUP J，KINNAERT M.Fault-tolerant control of wind turbines:a benchmark model［J］.IEEE Transactions on Control Systems Technology，2013，21（4）:1168-1182.

［2］SLOTH C，ESBENSEN T，STOUSTRUP J.Robust and fault-tolerant linear parameter-varying control of wind turbines［J］.Mechatronics，2011，21（4）:645-659.

［3］ROTONDO D，NEJJARI F，PUIG V，et al.Fault tolerant control of the wind turbine benchmark using virtual sensors/actuators［C］// Proceedings of the 8th IFAC Symposium on Fault Detection，Supervision and Safety of Technical Processes，August 29-31，2012，Mexico City，Mexico.2012:114-119.

［4］ZHANG H B，DANG C H，ZHANG J.H∞control of piecewise-linear systems under unreliable communication links［J］.Circuits Syst Signal Process，2012，31:1297-1318.

［5］BURKART R，MARGELLOS K，LYGEROS J.Nonlinear control of wind turbines:an approach based on switched linear systems and feedback linearization［C］//50th IEEE Conference on Decision and Control and European Control Conference，Dec 12-15，2011，Orlando，USA.2011:5485-5490.

［6］SLOTH C，ESBENSEN T，STOUSTRUP J.Active and passive fault-tolerant LPV control of wind turbines［C］//2010 American Control Conference，June 30-July 2，2010，Baltimore，USA.2010:4640-4646.

［7］ROTHENHAGEN K，FUCH F W.Doubly fed induction generator model-based sensor fault detection and control loop reconfiguration［J］.IEEE Transactions on Industrial Electronics，2009，56（10）: 4229-4238.

［8］PARKER M A，LI Ran，，FINNEY S J.Distributed control of a faulttolerant modular multilevel inverter for direct-drive wind turbine grid interfacing［J］.IEEE Transactions on Industrial Electronics， 2013，60（2）:509-522.

［9］Ruba M，Szabo L，Jurca F.Fault tolerant switched reluctance machine for wind turbine blade pitch control［C］//2009 International Conference on Clean Electrical Power，June 9-11，2009，Capri，Italy.2009:721-726.

［10］CUZZOLA F A，MORARI M.A generalized approach for analysis and control of discrete-time piecewise affine and hybrid systems［J］.Hybrid Systems:Computation and Control-Lecture Notes in Computer Sciences 2034，2001:189-203.

［11］JOHANSSON M，RANTZER A.Computation of piecewise quadratic Lyapunov functions for hybrid systems［J］.IEEE Transactions on Automatic Control，1998，43（4）:555-559.

［12］RANTZER A，JOHANSSON M.Piecewise linear quadratic optimal control［J］.IEEE Transactions on Automatic Control，2000，45 （4）:629-637.

［13］HASSIBI A，BOYD S.Quadratic stabilization and control of piecewise-linear systems［C］//Proceedings of the American Control Conference，June 21-26，1998，Philadelphia USA.1998:3659 -3664.

［14］PETTERSSON S，LENNARTSON B.LMI approach for stability and robustness of hybrid systems［C］//Proceedings of the American Control Conference，June 4-6，1997，Albuquerque，USA.1997:1714-1718.

［15］SLUPPHAUG O，FOSS B A.Constrained quadratic stabilization of discrete time uncertain nonlinear multi-model systems using piecewise affine state feedback［J］.International Journal of Control，1999，72:686-701.

［16］MIGNONE D，FERRARI-TRECATE G，MORARI M.Stability and stabilization of piecewise affine and hybrid systems:an LMI approach［C］//Proceedings of the 39th IEEE Conference on Decision and Control，December 12-15，2000，Sydney，Australia.2000: 504-510.

［17］年珩，周义杰，李嘉文.基于开绕组结构的永磁风力发电机控制策略［J］.电机与控制学报，2013，17（4）:79-85.

NIAN Heng，ZHOU Yijie，LI Jiawen.Control strategy of permanent magnet wind generator based on open winding configuration［J］.Electric Machines and Control，2013，17（4）:79-85.

［18］包广清，郑文鹏，毛开富.基于横磁通发电机的永磁直驱风力发电系统［J］.电机与控制学报，2012，16（11）:39-44.

BAO Guangqing，ZHENG Wenpeng，MAO Kaifu.Direct-driven wind turbine system with multiphase transverse flux permanent magnet generator［J］.Electric Machines and Control，2012，16 （11）:39-44.

［19］GANG F.Stability analysis of piecewise discrete-time linear systems［J］.IEEE Transactions on Automatic Control，2002，47（7）: 1108-1112.

［20］ESBENSEN T，SLOTH C.Fault diagnosis and fault-tolerant control of wind turbine［D］.Aalborg:Aalborg University，2009.

［21］HØJSTRUP J.Velocity spectra in the unstable planetary boundary layer［J］.Journal of the Atmospheric Sciences，1982，39（10）:2239 -2248.

［22］Munteanu I，Cutululis N-A，Bratcu A L，et al.Optimal control of wind energy systems［M］.London:Springer，2008.

［23］ØSTERGAARD K Z，BRATH P，STOUSTRUP J.Estimation of effective wind speed［J］.Journal of Physics:Conference Series，2007，75（1）:1-9.

（编辑:张诗阁）

Stochastic modelling and H∞fault tolerance control of WECS

SHI Yun-tao，HOU Yan-jiao，SUN De-hui，LI Zheng-xi
（Key Laboratory of Beijing for Field-bus Technology＆Automation，North China University of Technology，Beijing 100144，China）

Modelling and H∞fault tolerant control problem of wind energy conversion system（WECS）was studied with sensor and actuator faults.The normal stochastic piecewise affine models for WECS with multiple working points were established.Also the stochastic piece wise affine（PWA）models were proposed for WECS with generator speed sensor，power sensor gain loss faults and pitch angle actuator，generator actuator gain loss faults.A reliable piecewise linear quadratic state feedback regulator was designed for WECS with the actuator and sensor faults.A sufficient condition for existence of passive fault tolerant controller was derived and formulated as feasibility of a set of linear matrix inequalities.Simulation results of control systems confirm that they are capable of controlling the wind turbine exposed to multiple simultaneous sensors faults or actuators faults.Consequently，the reliability of wind turbines is improved.

fault tolerant control;stochastic PWA;WECS;H∞robust control

10.15938/j.emc.2015.03.016

TM 614

A

1007-449X（2015）03-0100-11

2014-03-03

国家自然科学基金面上项目（61473002）;北京市自然科学基金（4132021）

史运涛（1975—），男，博士，副教授，研究方向为风力发电机组的容错控制;

侯彦娇（1987—），女，硕士研究生，研究方向为风力发电机组的容错控制;

孙德辉（1962—），男，博士，教授，研究方向为现场总线自动化;

李正熙（1955—），男，博士，教授，研究方向为电力电子与电气传动、新能源。

史运涛