基于强跟踪的平方根UKF的卫星姿态确定算法

王松艳，李敏，张迎春，2，祝宝龙，李化义

（1.哈尔滨工业大学航天学院，黑龙江哈尔滨，150001;2.深圳航天东方红海特卫星有限公司，广东深圳 518057）

基于强跟踪的平方根UKF的卫星姿态确定算法

王松艳1，李敏1，张迎春1，2，祝宝龙1，李化义1

（1.哈尔滨工业大学航天学院，黑龙江哈尔滨，150001;2.深圳航天东方红海特卫星有限公司，广东深圳 518057）

针对受不确定性干扰的影响卫星姿态确定系统，SRUKF存在跟踪能力弱、估计精度低和鲁棒性差等问题，本文根据强跟踪滤波（STF）原理，提出了一种改进的强跟踪平方根UKF算法。该方法中，采用基于等价变化的方法来计算自适应渐消因子，避免了Jacobian矩阵的计算;引入两个多重自适应渐消因子矩阵，保证了协方差矩阵的对称性;利用改进的平方根分解方法，改善了滤波器的稳定性。实验仿真结果表明，相对于SRUKF和STF，本文提出的强跟踪平方根UKF具有更好的稳定性、鲁棒性和对突变状态的跟踪能力。

四元数;QR分解;卫星姿态确定系统;改进的强跟踪平方根UKF

0 引言

卫星姿态确定系统是卫星姿态控制系统的重要组成部分，其精度直接影响姿态控制系统的精度，通常采用滤波的方法从概率统计角度最优的估计出卫星姿态。由于卫星姿态确定系统的非线性，因此采用非线性滤波技术来估计卫星姿态的方法在工程上的到了广泛的应用。扩展卡尔曼滤波器（EKF）具有方法简单，容易实现等优点，在处理非线性估计问题中被广泛应用;但是EKF是将非线性方程通过Taylor展开做一阶近似处理，忽略其余高阶项，从而将非线性问题转化为线性。当系统非线性较强时，EKF违背局部线性假设，被忽略的高阶项会带来大的误差，导致EKF算法精度下降，甚至造成EKF算法的不稳定。另外EKF在线性化处理时需要计算雅克比（Jacobian）矩阵，其繁琐的计算过程导致该方法有时候难以实现［1－3］。

为了解决上述问题，Julier等提出了一种新的非线性滤波器——UKF。相对于EKF，UKF采用UT变换对非线性概率密度分布进行近似，具有不需要求导、实现简单、估计精度高等优点，被广泛应用姿态估计问题［4－5］。然而，UKF在数值计算中往往会存在舍入误差，可能会破坏系统估计误差协方差矩阵的非负定性和对称性，导致算法的收敛速度慢，甚至造成算法的不稳定。文献［6］针对该问题提出了一种平方根UKF（SRUKF）滤波算法，该方法借鉴kalman滤波中平方根分解滤波思想，在滤波的过程中采用矩阵的QR分解和Cholesky分解结果直接传播并更新协方差矩阵的平方根，解决了UKF算法中由计算误差可能引起的误差协方差负定问题，提高了滤波算法的计算效率和数值稳定性，文献［7］将该算法成功的应用到卫星姿态和角速度估计当中。

以上这些滤波方法都是针对精确模型进行应用，在模型不准确或发生突变的情况下，EKF、UKF和SRUKF都不具备较好估计精度、鲁棒性和跟踪能力。针对这些问题，周东华等提出了强跟踪滤波器（STF），STF具有较好关于模型不确定性的鲁棒性和较强的关于突变状态的跟踪能力［8］。文献［9］将STF理论思想与UKF相结合，并成功的应用到天文自主导航中，改善了系统的可靠性。然而，这两种方法都与EKF类似，都存在对非线性系统的一阶近似处理，仍然存在计算非线性函数的Jacobian矩阵等缺点，这限制了该方法的应用。而且，UKF在数值计算的过程中，由于舍入误差可能破坏误差协方差矩阵的非负定性，影响UKF的收敛速度和稳定性。

为此，本文以卫星姿态确定系统为背景，提出了一种基于改进的强跟踪平方根UKF的滤波算法。在该方法中，推导了基于等价描述的强跟踪滤波器框架，采用UT变化方法计算自适应渐消因子，避免Jacobian矩阵的计算。引入两个多重自适应渐消因子矩阵，保证了误差协方差矩阵的对称性，并从理论上证明其仍然满足正交原理。另外，为了避免数值计算的过程中，随着迭代计算的累加，积累的舍入误差可能会破坏系统估计误差协方差矩阵的非负定性和对称性，从而导致算法的收敛速度慢，甚至造成算法的不稳定的缺陷，采用协方差矩阵的平方根形式进行递推滤波，通过分析标准平方根UKF存在的缺陷，设计一种改进的平方根分解步骤，改善了滤波器的稳定性。实验仿真结果表明，相对于STUKF和SRUKF，本文提出的强跟踪平方根UKF具有更好的稳定性、鲁棒性和对突变状态的跟踪能力。

1 卫星姿态确定系统

1.1 系统状态方程

卫星姿态四元数被定义为［10－11］

式中:q13=nin（θ/2）;q0=cos（θ/2）;和θ分别为单位旋转向量和旋转角。

四元数满足如下约束:

用四元数表示的卫星运动学方程为

在无陀螺测量角速度的情况下，为了估计卫星的角速度，引入卫星姿态动力学方程

式中:ω=［ωxωyωz］T为坐标系中卫星的三轴角速度;J为系统的惯量矩阵;N（t）为外部控制力矩。

选取x=［q0q1q2q3ωxωyωz］T为系统状态变量，则有非线性状态方程

1.2 双向量法测量方程

双向量法是指利用安装在卫星中的加速度计得到的重力向量和磁强计得到的地磁场向量在载体坐标系中通过投影（映射）来计算卫星的姿态。文献［12］给出了双向量法测量模型下的欧拉角计算:

式中:g为当地重力加速度;gb=［gxgygz］T为加速度计测得的重力向量;Hb=［HbxHbyHbz］T为磁强计测得的磁场强度向量。

选取欧拉角z=［φθψ］T作为测量输出，根据欧拉角与四元数之间的关系，则得测量方程的映射为:

2 基于卫星姿态确定系统的STSRUKF算法

2.1 UKF算法

将式（5）和式（7）组成的卫星姿态确定系统用4阶龙格库塔法离散，得到如下非线性离散系统:

式中，xk=［q0，kq1，kq2，kq3，kωx，kωy，kωz，k］T为系统状态矢量，uk为控制输入向量，zk=［φkθkψk］T为测量矢量，wk和vk分别为状态系统高斯白噪声和测量系统高斯白噪声，它们的协方差分别为Qk和Rk。

针对上述卫星姿态确定系统的UKF算法如下［13］，在整个计算的过程中，四元数要按照式（9）进行归一化计算。

式中:λ=α2（n+κ）－n为复合刻度参数;α是一个比例因子，调节粒子的分布距离，一般取值0.001～1;β是一个调节参数，一般取值为β=2;κ是一个尺度参数，一般取κ=3－n。

2.2 强跟踪UKF算法

在模型精确的情况下，UKF可以得到很高精度的结果，但是卫星运行的实际空间环境是复杂多变的，导致卫星模型的不确定性，同时，空间环境的噪声统计特性也时常发生变化［14］。这使得UKF的估计精度下降，鲁棒性和跟踪能力变差。而强跟踪UKF在系统受到不确定干扰的情况下，仍具有较好估计精度、鲁棒性和跟踪能力。

强跟踪UKF和UKF之间的区别在于将自适应渐消因子μk+1引入到误差协方差矩阵，具体为:

式中，l是一个调节因子，ρ是一个遗忘因子，μk+1= diag（μ1，k+1，…，μn，k+1）是一个多重因子，文献［15］表明引入多重自适应渐消因子的效果要优于单个自适应渐消因子。

上述计算自适应渐消因子的过程中存在计算Jacobian矩阵，而求解Jacobian矩阵有时候是非常复杂和困难的。因此本文通过研究STF的等价描述，给出了一种无需计算Jacobian矩阵的自适应渐消因子的计算方法。

假设在未引入自适应渐消因子之前，误差的状态预测协方差矩阵，互协方差预测矩阵和输出预测协方差矩阵分别为:

将式（34）变形，得:

从上述描述中可以看出，自适应渐消因子计算按式（27）、（28）、（40）、（41）和式（31）来进行计算，有效的避免了Jacobian矩阵的计算。计算出自适应渐消因子后，按式（26）计算Pk+1|k，并用Pk+1|k替换式（35）和（36）当中的，得到Pxz，k+1和Pz，k+1。

2.3 强跟踪平方根UKF算法

在滤波的过程中，由于数值计算当中存在舍入误差，随着计算过程当中舍入误差的累积，有可能破坏滤波器的稳定性。因而，为了避免滤波器的发散，一般采用平方根分解的形式进行滤波。标准的平方根UKF其与UKF不同之处主要在于迭代计算的过程中采用误差协方差矩阵的平方根进行迭代计算，其分解形式如下［16］:

一步状态预测协方差矩阵的平方根分解:

式中:ξk为系统状态的Sigma采样点经过非线性函数f（·）离散传播后的点集k+1|k为状态一步预测值，χk为ξk经过非线性函数h（·）离散传播后的点k+1|k为输出预测值。

平方根UKF相对于UKF具有更好的鲁棒性、稳定性及估计精度。在平方根UKF的分解过程中，矩阵{S±OUUT}的Cholesky分解是用cholupdate {S，U，±O}表示，它要求矩阵必须是半正定的。但是在标准的平方根UKF中，按式（43）和式（45）更新协方差矩阵，实际如下:

在高阶系统中，当系统噪声为高斯白噪声的时候，为了获得较好的估计精度，一般取n+λ=3，因此λ是远小于零的。根据式（23）和（24）可知是负的，且，这使得按式（43）和（45）更新的矩阵很可能是负定的［3］。

另外，在平方根UKF中，按照式（47）更新状态误差协方差矩阵，实际如式（50）所示:

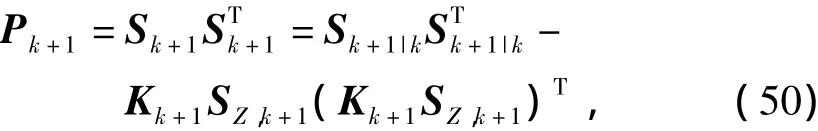
它要求等式右边必须是正定的，但是在数值计算过程中，等式右边很容易因为舍入误差的累积而破坏协方差矩阵的正定性。

针对上述问题，为了改善平方根UKF的稳定性，同时又能够保持平方根UKF的估计精度和鲁棒性，对平方根UKF作如下改进。

1）采用改进的状态误差一步预测协方差矩阵计算方法，文献［3］给出了一种改进的状态误差一步预测协方差矩阵的计算方法，如下:

式中:Hk+1按式（39）计算，采用式（56）更新状态误差协方差矩阵，避免了数值计算过程中因误差累积而破坏Pk+1正定性的问题。

根据上述描述，改进的强跟踪平方根分解UKF迭代计算过程与改进的强跟踪UKF的区别在于协方差矩阵的更新计算过程中，是以协方差矩阵的平方根进行迭代更新的。其具体步骤总结如下，在迭代的过程中四元数按照式（9）进行归一化:

2）计算Sigma点采样;

采用改进的强跟踪平方根分解UKF可以增强了UKF的鲁棒性和对突变状态的跟踪能力，同时还改善了滤波器在数值计算过程中的稳定性。另外，采用平方根分解可以提高数值计算过程中滤波器的估计精度，缩减计算量。

3 仿真结果及分析

为了验证本文提出的算法的有效性，本文将SRUKF，STF和STSRUKF算法对卫星姿态确定系统（11）进行姿态和角速度估计，仿真环境为Matlab R2010a软件平台。仿真参数设置为:

初始误差方差矩

采样时间Ts=1 s;仿真时长t=500 s。

为了比较三种算法和的鲁棒性和对突变状态跟踪性能，在仿真的过程中在200 s的时候引入突变状态量Δx=［00000.010.010.01］T，在300～400 s的时候引入模型不确定性。模型不确定性为

实验仿真结果如图1～图6所示，图1～图6分别是x轴角方向的速度估计绝对误差、y轴方向的角速度估计绝对误差、z轴方向的角速度估计绝对误差、滚转角的估计绝对误差、俯仰角的估计绝对误差和偏航角的估计绝对误差。

图1 x轴角速度估计绝对误差Fig.1Absolute estimation error of angular velocity about x axis

图2 y轴角速度估计绝对误差Fig.2Absolute estimation error of angular velocity about y axis

从图1～图6可以看出，在系统模型不确定性和外界干扰的时候，SRUKF、STF和ISTSRUKF的估计精度差不多。当系统发生状态突变的时候，SRUKF的估计结果很容易被影响，其估计精度是最差的，而且收敛速度最慢。STF算法估计的姿态误差和角速度误差精度在系统刚受到干扰的时候也会变差，但没有SRUKF算法改变的那么大，而且相对于SRUKF，STF能够很快的收敛，说明STF具有较好的对突变状态的跟踪能力。而本文提出的ISTSRUKF算法估计的角速度误差精度则几乎不受状态突变量的影响，说明其对突变状态的跟踪能力是最好的。另外，从图1～图6还可以看出，在模型具有不确定性的时候，估计结果最差的是SRUKF，其估计精度大大降低，滤波器不稳定，不具有匹配模型不确定性的鲁棒性，其次是STF的估计结果，相对于SRUKF来说，STF的估计结果变化较小，其估计精度也较好，具有一定的能够匹配模型不确定性的鲁棒性。而估计结果最好的是本文提出的ISTSRUKF，其估计结果几乎把发生改变，说明具有很好的能够克服模型不确定性的鲁棒性。

图3 z轴角速度估计绝对误差Fig.3Absolute estimation error of angular velocity about z axis

图4 滚转角估计绝对误差Fig.4Absolute estimation error of roll angle

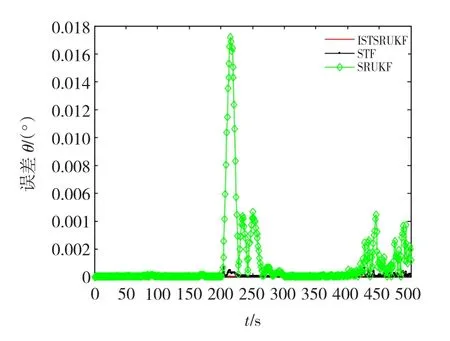
图5 俯仰角估计绝对误差Fig.5Absolute estimation error of pitch angle

图6 偏航角估计绝对误差Fig.6Absolute estimation error of yaw angle

4 结论

针对无陀螺卫星姿态和角速度估计问题，本文提出了一种ISTSRUKF算法。该方法中，采用基于等价变化的方法来计算自适应渐消因子，避免了Jacobian矩阵的计算;引入两个多重自适应渐消因子矩阵，保证了协方差矩阵的对称性;利用改进的平方根分解方法，改善了滤波器的稳定性。数值仿真结果表明，相对于SRUKF算法和STF算法，在卫星系统模型具有不确定性和受到干扰的时候，ISTSRUKF算法具有更好的鲁棒性、稳定性和对突变状态的跟踪能力。

［1］PSIAKI M L.Back ward smoothing extended Kalman Filter［J］.Journal of Guidance，Control and Dynamics，2005，28（5）:885－894.

［2］JOSEPH J，LAVIOLA JR.A comparison of unscented and extended Kalman filtering for estimating quaternion motion［C］//Proceedings of the 2003 American Control Conference，June 4－6，2003，Denver，USA.2003:2435－2440.

［3］JULIER S J，UHLAMNN J K，DURRANT-WHYTE H F.A new method for the nolinear transformation of means and covariances in fiters and estimators［J］.IEEE Transactions on Automatic Control，2000，45:477－482.

［4］SHOU Honien，LIN Chentsung，CHANG Chungliang.Micro-satellite attitude angle rate estimation unscened Kalman fiter approach［C］//Proceeding SCIE Annual Conference 2010，July 5－7，2010，Taipei，China.2010:1278－1290.

［5］吴盘龙，孔建寿.基于平方根UKF的水下方位目标跟踪［J］.南京理工大学学报，2009，33（6）:751－755.

WU Panlong，KONG Jianshou.Underwater bearing-only target tracking based on square-root UKF［J］.Journal of Nanjing University of Science and Technology，2009，33（6）:751－755.

［6］VAN DER MERWE R，WAN E A.The square-root unscented Kalman filter for stateand parameter-estimation［C］//Proceedings of the International Conference on Acoustics，Speech，and Signal Processing，June 1－3，2001，New York，USA.2001:3461－3464.

［7］姜雪原，马广富.基于平方根Unscented卡尔曼滤波的无陀螺卫星姿态估计［J］.南京理工大学学报，2005，29（4）:399－402.

JIANG Xueyuan，MA Guangfu.Gyroless satellite attitude estimation for square root unscented Kalman filter［J］.Journal of Nanjing University of Science and Technology，2005，29（4）:399－402.

［8］周东华，席裕庚，张钟俊.非线性系统次优渐消因子的扩展卡尔曼滤波［J］.控制与决策，1999，5（5）:1－6.

ZHOU Donghua，XI Yugen，ZHANG Zhongjun.Suboptimal fading extended Kalman filtering for nonliear systems［J］.Control and Decision，1999，5（5）:1－6.

［9］杨文博，李少远.基于强跟踪UKF的航天器自主导航间接量测滤波算法［J］.系统工程与电子技术，2011，33（11）:2485－2491.

YANG Wenbo，LI Shaoyuan.Autonomous navigation filtering algorithm for spacecraft based on strong tracking UKF［J］.Systems Engineering and Electronics，2011，33（11）:2485－2491.

［10］SHI Yong，HAN Chongzhao，Adaptive UKF method with applications to target tracking［J］.Journal of Acta Automatica Sinica，2011，37:755－759.

［11］JWO Dahjing，CHUNG Fongchi.Fuzzy adaptive unscented Kalman filter for ultra-tight GPS/INS integration［C］//Proceedings of 2010 International Symposium on Computational Intelligence and Design，October 29－31，2010，Hangzhou，China.2010: 229－235.

［12］章仁伟.卫星姿态动力学与控制［M］.北京:北航大学出版社，2005.

［13］周卫东，乔相伟，吉宇人，等.基于四元数平方根UKF算法的SINS/GPS紧组合导航系统研究［J］.系统工程与电子技术，2010，32（12）:2643－2647.

ZHOU Weidong，QIAO Xiangwei，JI Yureng，et al.SINS/GPS tightly integrated navigation system based on quaternion square root unscented Kalman filter［J］.Systems Engineering and Electronics，2010，32（12）:2643－2647.

［14］李璟璟，张迎春，李华义，等.ASUKF方法在航天器自主导航中的应用［J］.哈尔滨工程大学学报，2011，32（5）:575－580.

LI Jingjing，ZHANG Yingchun，LI Huayi，et al.Application of ASUKF in autonomous spacecraft navigation［J］.Journal of Harbin Engineering University，2011，32（5）:575－580.

［15］钱华明，黄蔚，孙龙，等.基于多重次渐消因子的强跟踪UKF姿态估计［J］.系统工程与电子技术，2013，35（3）:580－585.

QIAN Minghua，HUANG Wei，SUN Long，et al.Attitude estimation of strong tracking UKF based on multiplie fading factors［J］.Systems Engineering and Electronics，2013，35（3）:580－585.

［16］李鹏，宋申民，段广仁.改进的平方根UKF及其在交会对接中的应用［J］.电机与控制学报，2010，14（11）:101－105.

LI Peng，SONG Shenmin，DUAN Guangren.Improved square root unscented Kalman filter and its application in rendezvous and docking［J］.Electric Machines and Control，2010，14（11）:101－105.

［17］KAMINSKI P G，BRYSON A E，SCHMIDT S F.Discrete square root filtering:a survey ofcurrent techniques［J］.IEEE Transactions on Automatic Control，1970，16（6）:727－736.

（编辑:张诗阁）

Strong tracking unscented Kalman filter algorithm based-on satellite attitude determination system

WANG Song-yan1，LI Min1，ZHANG Ying-chun1，2，ZHU Bao-long1，LI Hua-yi1
（1.College of Astronautics，Harbin Institute of Technology，Harbin 150001，China;
2.Shenzhen Aerospace Dong-Fang-Hong HIT Satellite Company Ltd，Shenzhen 518057，China）

When the satellite attitude determination system is disturbed by uncertain factors，square-root unscented Kalman filter（SRUKF）is featured by low accuracy，bad tracking ability and poor robustness.In order to overcome these defects of SRUKF，an improved strong tracking squared-root Kalman filter （ISTSRUKF）based-on satellite attitude determination system was proposed.To avoid calculating the Jacobian matrices，the fading factors were calculated by using equivalent description of fading factors.To ensure the symmetry of covariance matrix，two multiple fading factors matrices were introduced.To improve the stability of filter，a modified square-root decomposition method was adopted.The simulation results show that improved strong tracking square root UKF has best stability，robustness and mutation status tracking capability than square-root UKF and strong tracking filter.

quaternion;QR decomposition;satellite attitude determination system;improved strong tracking square-root unscented Kalman filter（ISTSRUKF）

10.15938/j.emc.2015.03.017

V 249.32

A

1007－449X（2015）03－0111－08

2013－10－22

国家自然科学基金（61304237）;国防重点实验室微小型航天器技术开放基金（20090450126）

王松艳（1976—），女，博士，副教授，研究方向为飞行器姿态估计与控制;

李敏（1989—），男，硕士，研究方向为非线性滤波技术及其在卫星导航、姿态估计中的应用;

张迎春（1961—），男，教授，博士生导师，研究方向为卫星姿态估计与控制，卫星总体设计，卫星控制系统设计及故障诊断;

祝宝龙（1990—），男，硕士，研究方向为网络化控制及滤波;

李化义（1978—），男，博士，讲师，研究方向为卫星编队及控制。

李敏