含双馈风电场的互联电力系统广域阻尼协调控制

索江镭，胡志坚，仉梦林，张子泳，刘宇凯

（1.武汉大学电气工程学院，湖北武汉 430072;2.西安交通大学电力设备电气绝缘国家重点实验室，陕西西安 710049）

含双馈风电场的互联电力系统广域阻尼协调控制

索江镭1，2，胡志坚1，2，仉梦林1，2，张子泳1，2，刘宇凯1，2

（1.武汉大学电气工程学院，湖北武汉 430072;2.西安交通大学电力设备电气绝缘国家重点实验室，陕西西安 710049）

针对大区域电网互联以及大规模双馈风电场并网所面临的区域低频振荡问题，提出一种综合考虑同步发电机与双馈风力发电机的广域阻尼控制策略;并采用一种迭代次数较少、不易陷入局部最优解的新型优化算法——均值方差映射算法进行控制器参数协调配置，通过与传统智能算法的比较，证明了该方法的优越性;含双馈风电场的四机两区测试系统的仿真结果表明，提出的方法能有效提高大规模双馈风电场并网背景下的互联电力系统区域低频振荡阻尼能力。

双馈风电场;互联电力系统;广域阻尼控制器;均值方差映射算法;控制器参数协调优化

胡志坚（1969—），男，教授，博士生导师，研究方向为电力系统运行与控制、智能电网、风力发电并网运行与控制等;

仉梦林（1987—），女，博士研究生，研究方向为含风电并网的电力系统优化调度;

张子泳（1987—），男，博士研究生，研究方向为大型互联电力系统低频振荡分析与阻尼控制、新能源优化调度研究;

刘宇凯（1989—），男，硕士研究生，研究方向为大型互联电力系统阻尼控制。

0 引言

21 世纪以来，能源危机以及环境污染问题日趋严峻，而风能作为一种可再生、无污染的清洁能源，受到了世界各国的广泛关注［1］。近年来，随着风力发电技术的不断进步，风电装机容量与风电并网容量持续稳步增长。由于风能资源往往远离负荷中心，风电接入也由原来的配电网转变为输电网，大规模风电并网以及远距离的风电输送将改变系统原有的阻尼特性，进而对电网的安全稳定带来一定的影响［2－3］。因此，从提高互联电力系统区域阻尼特性角度出发，应将风电的影响以及改善措施考虑在内［4］。

文献［5］推导出适用于小干扰稳定的双馈风力发电机数学模型，研究了不同风电穿透率下的双馈风力发电机对系统阻尼的影响，从机理上分析了当系统风电穿透率的增加，系统阻尼比呈现出先增加再减小的过程，并通过PSD－BPA进行了仿真验证，可惜的是文中并未提出双馈风电场并网后，改善系统阻尼的措施。文献［6］提出了一种针对双馈风力发电机的电力系统稳定器（DFIG－PSS），它采用的是风电场端电压相角作为控制器的输入，并附加到风力发电机转子侧变频器以阻尼系统振荡，通过仿真证明其对本地振荡有着明显的抑制作用，但并未有效解决区间振荡。对此，文献［7］与文献［8］分别提出将广域信号附加到风力发电机转子侧变频器的有功和无功控制环节，仿真结果表明通过在双馈风力发电机转子侧引入广域控制环节，能够改善双馈风力发电机并网给系统阻尼带来的负面影响。

上述控制方法仅针对风电场侧考虑抑制区域振荡的问题，而并未将主导区域振荡的同步发电机进行综合考虑。因此，本文将双馈风力发电机的广域阻尼控制器与同步发电机的广域阻尼控制器一起纳入提高区域低频振荡的措施进行全局设计，并对由此引发的控制器参数之间的相互协调问题，采用新型优化算法——均值方差映射算法［9］进行控制器参数配置，以避免传统算法迭代次数多、容易陷入局部最优的缺点。

1 互联系统广域阻尼控制策略

本文提出的广域阻尼控制器的主要设计思路如下:首先对含双馈风电场的系统进行小干扰稳定分析;再引入同步发电机的附加广域阻尼控制器以及双馈风力发电机的附加广域阻尼控制器;最后通过协调优化，对控制器内部相关参数进行调整，以达到提高系统阻尼的目的。本文以如图1所示的两区域系统进行分析说明，采用的双馈风力发电机相关参数见文献［10］。

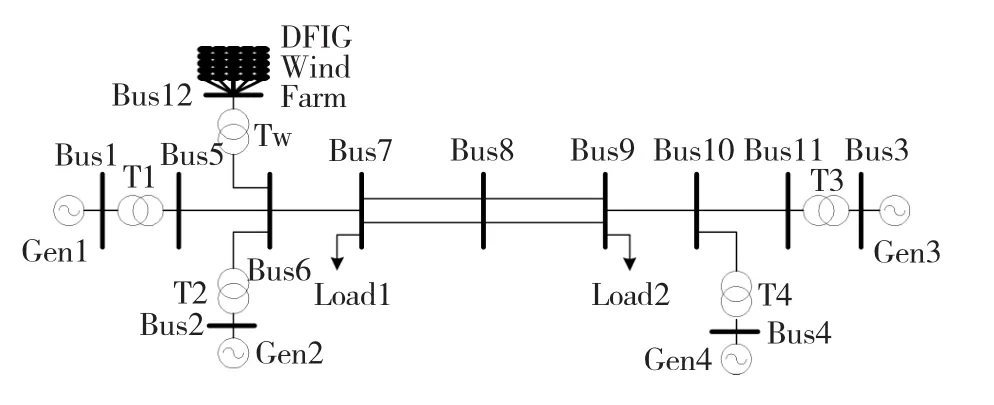
图1 含双馈风电场的四机两区模型Fig.1Model of two areas with four generators and DFIG

1.1 含双馈风力发电机的系统特征值分析

根据本文第一节所述的双馈风力发电机动态模型，列出系统动态方程为

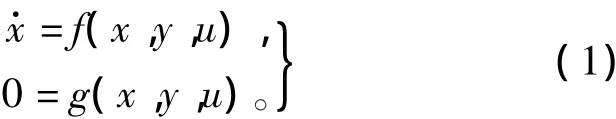
在系统稳定运行点处对式（1）进行线性化，可得系统特征矩阵方程为

当给定风速为14 m/s时，计算系统特征值如表1所示。

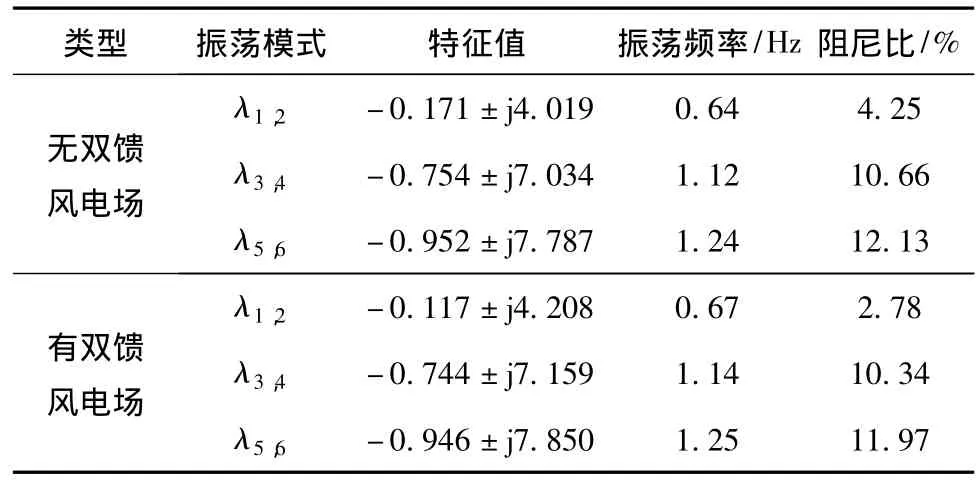
表1 系统特征值计算结果Table 1Calculation results of system eigenvalues

由表1可知，系统共有3组振荡模式。其中，特征根λ1，2所对应的模式为区间模式，λ3，4与λ5，6对应的为本地模式。当双馈风电场并网后，并未增加系统的主导振荡模式，但对系统的振荡频率与阻尼比都产生了不同程度的影响。其中，对振荡频率以及本地模式的阻尼比影响较小，而对区间模式的阻尼比影响较大，且其影响是负面的。因此，有必要考虑增加广域阻尼控制器，对系统区间阻尼不足的问题进行改善。

1.2 同步发电机的广域阻尼控制策略

针对系统区域阻尼不足的问题，传统方法是在同步发电机励磁系统中引入广域阻尼控制器［11］，其控制策略如图2所示。

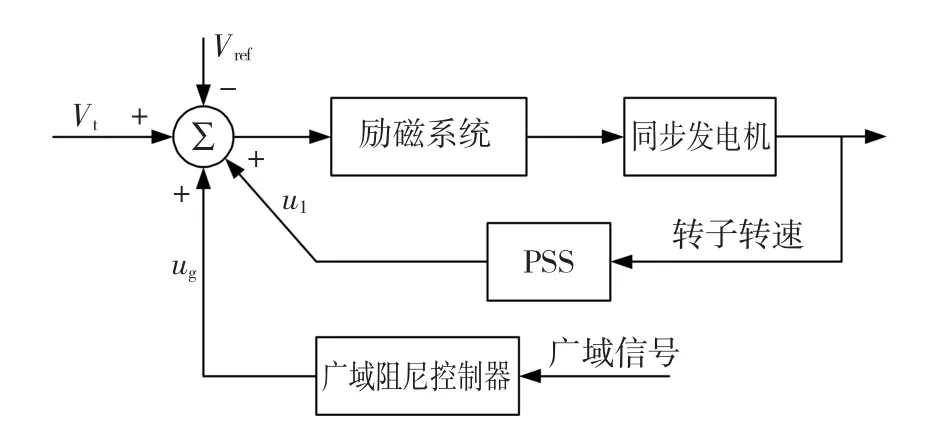
图2 同步发电机的广域阻尼控制策略Fig.2Wide-area damping control strategy of synchronous generator

对于图1所示的四机两区系统，选取联络线有功作为广域阻尼控制器的输入信号，而控制器输出信号则分别加在与系统主导振荡模式强相关的同步发电机G1和G3的励磁系统侧，控制器内部结构如图3所示。

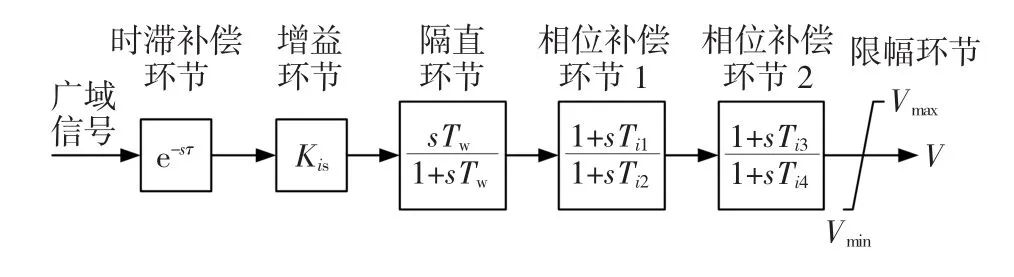
图3 同步发电机的广域阻尼控制器结构Fig.3Structure of wide-area damping controller of synchronous generator

上图中，i=1和3分别代表发电机G1和G3侧的广域阻尼控制器。采用极点配置法［12］，分别针对含双馈风电场与不含双馈风电场两种情况的系统进行控制器设计，并对加入广域阻尼控制器后的系统进行特征值计算，如表2所示。

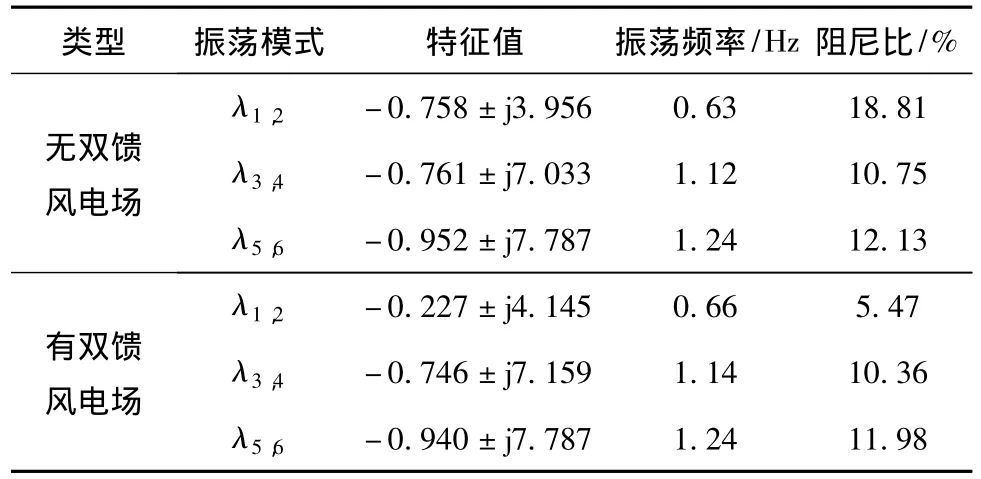
表2 系统特征值计算结果Table 2Calculation results of system eigenvalues

由表2可知，在无风电场的情况下，对系统配置广域阻尼控制器，可有效提高系统区域阻尼，改善系统动态性能。但在有风电场情况下，通过上述方法，虽对提高区域系统阻尼有一定的作用，但效果并不理想。因此，本文考虑在采用传统方法的基础之上，同时在风电场侧加入广域阻尼控制器，以提高系统区域阻尼特性。

1.3 双馈风力发电机的广域阻尼控制策略

根据低频振荡的产生机理，电力系统机电振荡是由同步发电机转子上的不平衡转矩所造成的。因此，针对双馈风力发电机，可以利用其有功可控的特性，在转子侧变频器加入控制器，以此产生附加电气转矩来阻尼系统机电振荡，具体控制策略如图4所示。

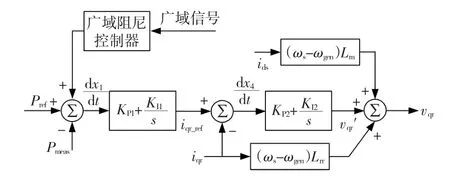
图4 双馈风力发电机的广域阻尼控制策略Fig.4Wide-area damping control strategy of DFIG

与同步发电机的广域阻尼控制器类似，针对系统区域阻尼不足的问题，本文考虑选取同步发电机G1与G3之间的转速差作为控制器的输入信号，控制器内部结构如图5所示。

图5 双馈风力发电机的广域阻尼控制器结构Fig.5Structure of wide-area damping controller of DFIG

1.4 广域阻尼控制器参数协调优化

根据上文分析，本文从同步发电机侧以及风电场侧两个方面综合考虑系统稳定性问题，提出采用如图6所示的广域阻尼控制策略，对同步发电机以及风电场进行协调控制，以提高系统区域阻尼。

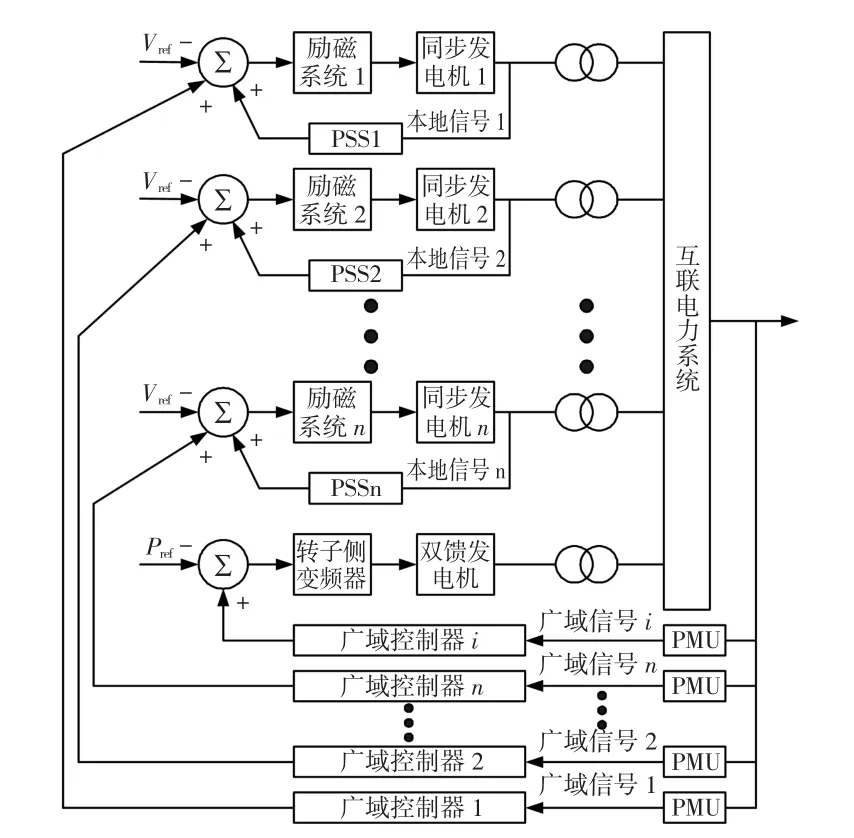
图6 广域阻尼控制全局策略图Fig.6Wide-area damping control strategy of DFIG

而对于控制器内部具体参数的设置，通常有极点配置法、增益裕度法、H∞法以及优化配置法等。考虑到本文涉及到多个广域阻尼控制器，需要对不同控制器的参数进行协调设置，通常采用优化配置法，可较好解决此类问题［13］。

根据经典控制理论可知，系统稳定的基本条件是:所有特征根均位于虚轴的左半边，并且特征根实部越小，系统越稳定。因此，定义本文优化算法的目标函数为

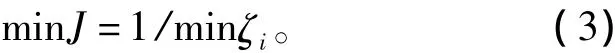
上式中，ζi为系统第i个特征值的阻尼比，而广域控制器内部除隔直环节外（本文取隔直时间常数Tw=T'w=5s），其它参数构成的解向量为

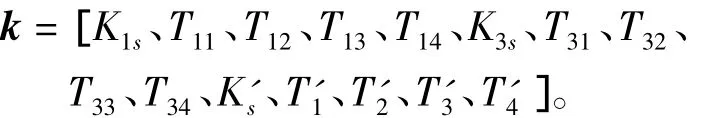
对于以上优化问题，解决方法有很多，例如:遗传算法、粒子群算法、差分进化算法、蚁群算法、细菌觅食算法、人工免疫算法等等。然而针对具体问题，选择不同算法的主要依据是在避免陷入局部最优的同时，尽量使算法的迭代次数少、收敛速度快、寻优精度高。为此，本文将采用一种新的优化算法:均值方差映射算法。

2 均值方差映射算法

均值方差映射算法是一种全新的种群随机优化算法，它最显著的特点是采用映射函数，将解空间限定在0到1之间，并且其映射函数随着解空间的均值和方差的变化而变化，和传统智能优化算法相比具有收敛速度快、不易陷入局部最优等优点。

2.1 初值设置及终止条件

均值方差映射算法初值包括:解向量初值X0、动态种群维数n、选择变异个数m、形状收放因子fs。其中，解向量初值设置为0到1之间的任意随机数，其他参数可根据具体情况进行调整。而均值方差映射算法的迭代终止条件与其他智能优化算法类似，可选取最大迭代次数或者最小适应度函数误差作为评判标准。

2.2 动态种群筛选

均值方差映射算法将适应度最好的n个解向量储存在动态的种群表当中。在该表中，n个解向量按照适应度从低到高排列，若后续步骤产生了比表中n个解向量适应度更好的解，则自动淘汰种群表中适应度最差的那组解。因此，可以保证种群表中的n个解向量始终为当前寻找到最优的n组解。然后分别计算k个解向量的均值和方差。若种群表发生更新，则需重新计算k维解向量的均值与方差，其计算公式为

2.3 亲代与子代

均值方差映射算的亲代定义为当前适应度最好的解向量，即排列在动态种群表第一排的解向量。而其子代则由亲代通过:选择——变异——克隆，3个步骤产生。

2.3.1 选择

在亲代的解向量中，从k个解中连续选取m个解进行下一步的变异过程。当迭代结束后，选择窗向后顺移一位，具体过程如图7所示。

2.3.2 变异

变异是均值方差映射算法的核心步骤，其思想是通过映射函数，将上一步选择的m个解进行变异。第1次选择的m个解的变异方法通过均匀分布的随机函数，生成一个范围在0到1之间的随机值。第1次之后选择的m个解的变异方法则是通过如下映射函数生成为

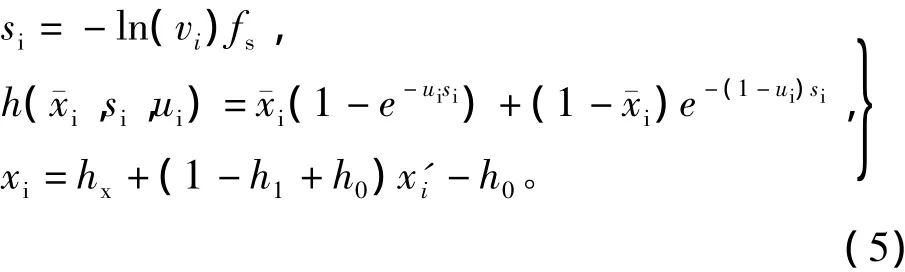
式中:hx=h（ui=x'）;h0=h（ui=0）;h1=h（ui=1）。

式（5）中，si为形状因子，fs为2.1节提到的形状收放因子。图8显示的是当均值¯xi=0.5时的均值映射函数曲线，其中横坐标与纵坐标分别代表归一化的解向量和其通过映射函数变异后的结果。从图中可以看出，当形状因子si随方差的减小而增大时，曲线将变得越来越平缓，因此算法将从全局搜索逐渐过渡到局部搜索，具有一定自适应能力。而fs决定了算法的初始搜索能力，即当fs较小时，映射曲线较陡峭，此时算法具有更好的初始全局搜索能力;当fs较大时，映射曲线较平缓，此时算法具有更好的初始局部搜索能力。因此，在初值设置阶段，需根据具体的情况，对fs进行调整，以达到最佳的优化效果。

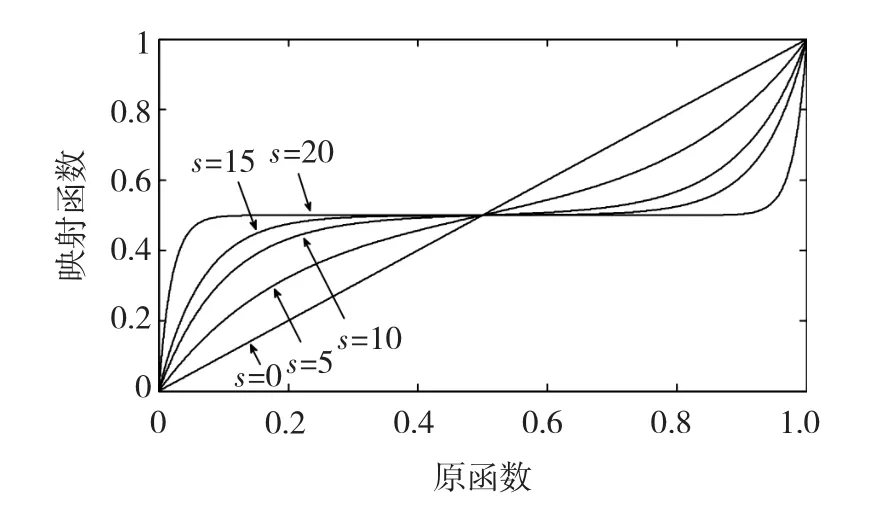
图8 映射函数曲线Fig.8Curve of mapping function

2.3.3 克隆

通过上述两步，子代中的m个解由亲代中相应的m个解变异而来，而子代中剩余的k－m个解则由亲代中相应的k－m个解克隆而来，所谓克隆则是指这k－m个解直接与亲代保持一致，未发生任何改变。

2.4 反归一化

由于均值方差映射算法将解空间限定在［0，1］的范围内，但适应度函数并未做归一化处理，因此每次迭代后计算适应度函数时，应对解空间进行反归一化为

其中，X代表归一化后的解空间，U和L分别代表其上限与下限，Y代表反归一化后的结果。

2.5 算法流程

通过上述过程的不断循环，可完成均值方差映射算法流程，如图9所示。

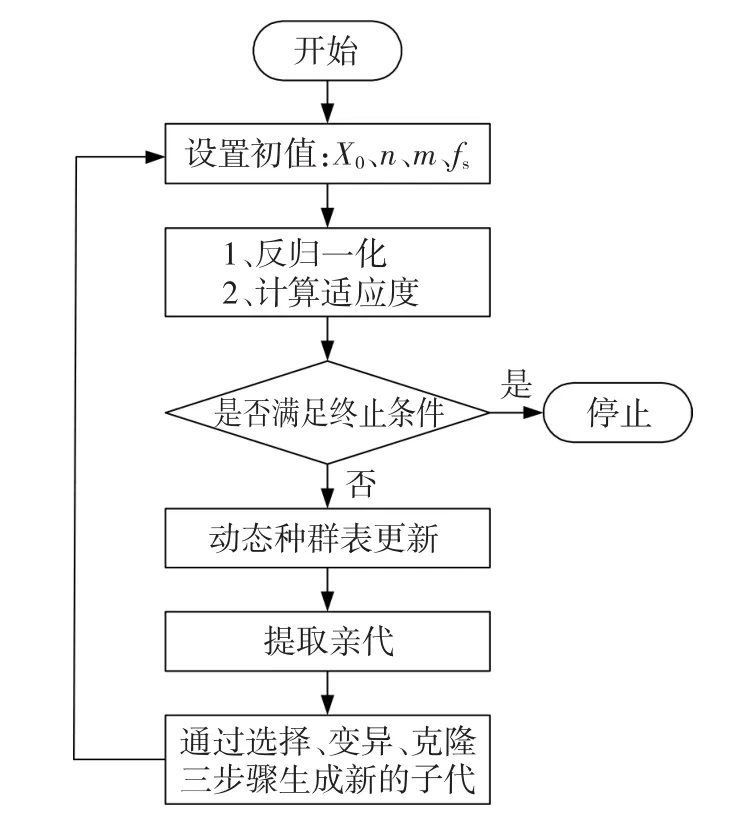
图9 均值方差映射算法流程Fig.9The algorithm flow of MVMO

3 仿真结果

本文在Matlab/SIMULINK环境中建立了仿真模型，并设定广域控制器各增益环节Ks的寻优范围为［0，100］，广域控制器中各相位补偿环节的时间常数T的寻优范围为［0，100］;设定均值方差映射算法的动态种群维数n为3，选择变异个数m为3，收放因子fs为1.5。图10为本文算法（MVMO）与传统智能算法的迭代对比结果，其中包括粒子群算法（particle swarm optimization）、遗传算法（genetic algorithm）、细菌觅食算法（bacterial foraging）。

图10 不同算法迭代对比图Fig.10Comparison diagram of different iterative algorithms

从图10中可以看出，均值方差映射算法较其他算法有着迭代次数少、收敛速度快的优势。针对本文优化目标，粒子群算法收敛速度虽比遗传算法快，耗时比细菌觅食算法少，但在使用过程中，有较大概率陷入局部最优，最终导致控制器设计失败。而本文采用的方差映射优化算法，其算法流程简单，寻优范围为全局搜索，且映射函数具有自适应特性，在处理本文优化问题时表现出迭代次数少、耗时短、不易陷入局部最优等优点，最终控制器的良好表现奠定了一定的基础。

为验证上述控制器参数以及本文控制策略的有效性，本文分两种情况进行仿真验证:

1）设定风电场风速恒定为14 m/s，稳定运行1 s后，同步发电机G1机端电压上升10%，持续时间为60 ms。对比系统加入广域阻尼控制器和未加入时，部分参数的动态响应如图11所示。

2）设定风电场初始风速为14 m/s，稳定运行1 s后，风速突然减小40%。对比系统加入广域阻尼控制器和未加入时，部分参数的动态响应如图12所示。

从以上仿真可以看出，在发生小扰动时，通过本文的控制策略，互联电力系统的功角、联络线功率、母线电压、风电场功率、风力发电机转速等参数扰动得到了明显的抑制，控制器参数之间能够相互协调，区域间低频振荡问题得到了较好的解决。

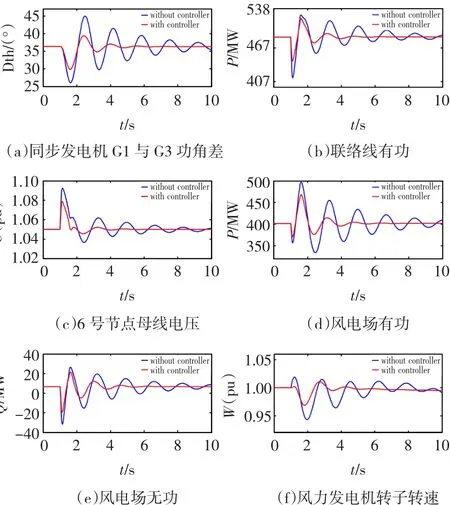
图11 系统动态响应Fig.11The dynamic response of system

图12 系统动态响应Fig.12The dynamic response of system

4 结论

1）针对大规模双馈风电场并网与区域电网互联可能造成的区域低频振荡问题，本文提出了可同时控制同步发电机与风电场的广域控制策略，该策略利用广域测量系统将广域控制信号分别附加到同步发电机励磁侧电压控制环节以及双馈风力发电机转子侧变频器有功控制环节，对含双馈风电场的四机两区系统进行了仿真，验证了该控制策略的有效性。

2）针对广域控制策略中，不同控制器之间的参数协调问题，本文提出使用均值方差映射算法进行优化配置，通过与粒子群算法、遗传算法以及细菌觅食算法的比较，证明该方法在处理本文优化问题时具有迭代次数少、耗时短、不易陷入局部最优等优点，所得到的控制器参数之间能够相互协调。

3）本文提出的控制策略以及协调优化算法并不局限于本文的算例系统，具有一定的一般性，针对未来“风光储”等新能源技术的大规模应用，该方法亦可得以推广。

［1］DURGA Gautam，VIJAY Vittal，TERRY Harbour.Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems［J］.IEEE Transactions on Power Systems，2009，24（3）:1426－1434.

［2］张丽英，叶廷路，辛耀中，等.大规模风电接入电网的相关问题及措施［J］.中国电机工程学报，2010，30（25）:1－9.

ZHANG Liying，YE Tinglu，XIN Yaozhong，et al.Problems and measures of power grid accommodating large scale wind power［J］.Proceedings of the CSEE，2010，30（25）:1－9.

［3］李媛媛，邱跃丰，马世英，等.风电机组接入对系统小干扰稳定性的影响研究［J］.电网技术，2012，36（8）:50－55.

LI Yuanyuan，QIU Yuefeng，MA Shiying，et al.Impact of grid-connected wind turbine generators on small signal stability of power grid［J］.Power System Technology，2012，36（8）:50－55.

［4］张子泳，胡志坚，胡梦月，等.含风电的互联电力系统时滞相关稳定性分析与鲁棒阻尼控制［J］.中国电机工程学报，2012，32 （34）:8－17.

ZHANG Ziyong，HU Zhijian，HU Mengyue，et al.Delay-dependent stability analysis and robust damping control of power system with wind power integration［J］.Proceedings of the CSEE，2012，32（34）:8－17.

［5］陈树勇，常晓鹏，孙东华，等.风电场接入对电力系统阻尼特性的影响［J］.电网技术，2013，37（6）:1570－1577.

CHEN Shuyong，CHANG Xiaopeng，SUN Huadong，et al.Impact of grid-connected wind farm on damping performance of power system［J］.Power System Technology，2013，37（6）:1570－1577.

［6］GEORGIOS Tsourakis，BASIL M Nomikos，COSTAS D Vournas.Contribution of doubly fed wind generators to oscillation damping［J］.IEEE Transactions on Power Systems，2009，24（3）:783－791.

［7］张子泳，胡志坚，李勇汇.并网型双馈式风力发电系统广域阻尼控制器设计［J］.高电压技术，2011，37（1）:157－163.

ZHANG Ziyong，HU Zhijian，LI Yonghui.Design of wide－area damping controller of grid-tied wind generation system based DFIG［J］.High Voltage Engineering，2011，37（1）:157－163.

［8］FAN Lingling，YIN Haiping，MIAO Zhixin.On active/reactive power modulation of DFIG-Based wind generation for interarea oscillation damping［J］.IEEE Transactions on Power Systems，2011，26（2）:513－521.

［9］ERLICH I，VENAYAGAMOORTHY G K，NAKAWIRO W.A mean-variance optimization algorithm［C］//Proceedings of IEEE Congress on Evolutionary Computation，July 18－23，2010，Barcelona，Spain.2010:1－6.

［10］LUIS M Fernandeza，FRANCISCO Jurado，JOSE Ramon Saenz.Aggregated dynamic model for wind farms with doubly fed induction generator wind turbines［J］.Renewable Energy，2008，33 （1）:129－140.

［11］胡志坚，赵义术.计及广域测量系统时滞的互联电力系统鲁棒稳定控制［J］.中国电机工程学报，2010，30（19）:37－43.

HU Zhijian，ZHAO Yishu.Robust stability control of power systems based on WAMS with signal transmission delays［J］.Proceedings of the CSEE，2010，30（19）:37－43.

［12］张子泳.胡志坚，李勇汇.大型双馈风力发电系统小信号动态建模及附加阻尼控制器设计［J］.电力系统保护与控制，2011，39（18）:127－133.

ZHANG Ziyong，HU Zhijian，LI Yonghui.Small signal dynamic modelling and additionaller damping controller designing for large wind generation system based on DFIG［J］.Power System Protection and Control，2011，39（18）:127－133.

［13］MISHRA Y，MISHRA S，TRIPATHY M，et al.Improving stability of a DFIG-Based wind power system with tuned damping controller［J］.IEEE Transactions on Energy Conversion，2009，24（3）: 650－660.

（编辑:刘琳琳）

Wide-area damping coordination control in the interconnected power system with doubly fed wind farm

SUO Jiang-lei1，2，HU Zhi-jian1，2，ZHANG Meng-lin1，2，ZHANG Zi-yong1，2，LIU Yu-kai1，2
（1.School of Electrical Engineering，Wuhan University，Wuhan 430072，China; 2.State Key Laboratory of Electrical Insulation and Power Equipment，Xi’an Jiaotong University，Xi’an 710049，China）

A wide-area damping control strategy comprehensively considering synchronous generators and doubly fed induction generators was proposed which is based on the interarea low frequency oscillation problem caused by large area interconnected power grid and massive grid connected doubly fed wind farms.Also，a new optimization algorithm called Mean-Variance Mapping Optimization algorithm with the advantage of fewer iterations and not easy to fall into local optimal solution was adopted to coordinate the configuration of controller parameters.And the superiority of this new method is proved by contrast with the traditional intelligent algorithms.At last，interarea low frequency oscillation problem in interconnected power systems with massive grid connected doubly fed wind farms was effectively solved by the proposed method，which is validated by the simulation results a four-machine and two-region test system with a doubly fed wind farm.

doubly fed induction generator（DFIG）;interconnected power systems;wide-area damping controller;mean-variance mapping optimization algorithm;coordination and optimization of controller parameters

10.15938/j.emc.2015.03.009

TM 71

A

1007－449X（2015）03－0054－07

2014－01－24

高等学校博士学科点专项科研基金（20110141110032）;西安交通大学电力设备电气绝缘国家重点实验室资助（EIPE13205）

索江镭（1984—），男，博士研究生，研究方向为大型互联电力系统低频振荡分析与阻尼控制;

索江镭