例析运用数学方法解决实验问题的误区——以数据处理、误差分析为例

朱　琦

(江苏省南京市第二十九中学，江苏　南京　210036)

例析运用数学方法解决实验问题的误区——以数据处理、误差分析为例

朱琦

(江苏省南京市第二十九中学，江苏南京210036)

名师简介：朱琦，江苏省特级教师、首批教授级高级教师，南京市学科带头人，南京物理学会常务理事，江苏省、南京市劳动模范.近年来先后有80多篇文章在各级刊物上发表，主编、参编十几本教科书或教学用书，主持多个教育规划课题.

摘要：处理实验问题时，需要关注诸多方面的因素，其中正确应用数学方法进行实验数据的处理、误差分析等又是解决该方面问题的关键之一，本文结合具体案例，分析用数学方法解决实验问题中存在的误区，提出了有针对性的教学策略.

关键词：物理实验；数学方法；误区；教学策略

物理学是以实验为基础的学科，在中学物理中，物理实验占据非常重要的地位，而数学在物理中起着重要的工具作用.处理实验问题时，需要关注的因素很多，正确应用数学方法进行实验数据的处理、误差分析等是其关键.下面就以数据处理、误差分析为例，分析学生在解实验题中存在的误区，探究应对策略.

误区一忽视物理实验数据处理的特殊性与灵活性，作单纯数学运算对待

例1在研究匀变速直线运动的实验中，算出小车经过各计数点的瞬时速度如下：

计数点序号123456计数点对应时刻(s)0.10.20.30.40.50.6通过计数点的速度(cm/s)44.062.081.0100.0110.0168.0

为了求出加速度，合理的方法是().

B. 根据实验数据画出v-t图像，量出其倾角，由公式a=tanα算出加速度

D. 依次算出通过连续两个计数点间的加速度，算出平均值作为小车的加速度

学生解题误区：这是一道典型的数据处理方法选择题，一些学生在作答这样的问题时，疑惑丛生，选什么的都有，其中选B的亦不在少数，这显然是把这种数据处理当成了单纯的数学中的斜率计算，忽视了物理与数学的差异.

对策：可以列举在不同情况下的物理图像，比如在做“测定电池的电动势和内阻”的实验时， 针对实验器材的不同，在已知路端电压和干路总电阻的情况下，可以作出图1，在测出路端电压和干路中电流强度的情况下，可作出图2，从这些图像可看出，在平面直角坐标系里，两坐标的分度大小往往不相同，其单位一般也不相同，两坐标代表的物理量丰富多彩，其直线不一定过原点.再与数学中的斜率(如图3)进行对比，使学生认识到物理与数学的差别，故物理这类问题中的斜率k，不能像数学中斜率k=tanα那样简单对待，应如例1中C选项那样处理才是合理的.

图1

图2

误区二偏差判断时，无视数据处理方法

例2在利用单摆测定重力加速度的实验中，一位学生在不同摆长l的条件下，测得单摆的周期T与摆长l的关系如下：

次数12345l/m0.80000.90001.00001.10001.2000T/s1.801.902.012.112.20T2/s23.243.614.044.454.84

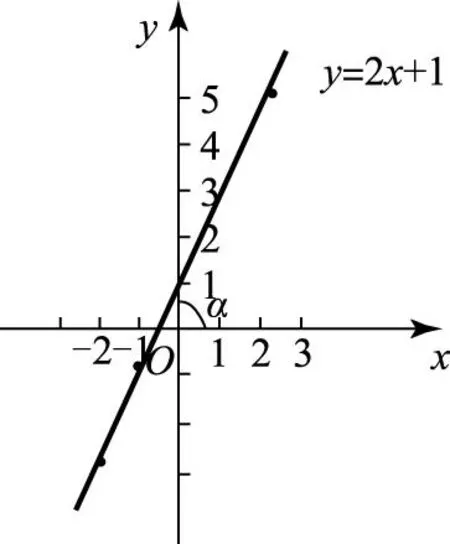
图3

(1) 试在坐标纸上画出T2与l的关系图线，利用图线计算出的重力加速度g=________m/s2.(保留3位有效数字)

(2) 若测量摆长l时漏测了摆球的半径r，利用T2-l图线测得的重力加速度g的值________(偏大、不变或偏小).

图4

图5

对策：选取不同例证进行比较分析，使学生真正体会到误差分析不能离开实验所选的数据处理方法，本题中的漏测是误差的一种，即粗大误差也叫过失误差，选用不同的数据处理方法，对误差的影响不同.就本例来说，用了一种典型的化曲为直的图像处理方法，正好可以消除过失误差的影响.这种方法的特点是与数学知识相结合，通过求斜率、截距确定某些物理量，这在物理实验数据处理中是比较常见的.以本例看，从图像分析，当漏测r时，相当于以线长l′为摆长，这时T2=kl′=

k(l-r),由数学知识可知，这时的图线斜率不变，那么重力加速度g的值也不变.如图5所示，a图线为正常未漏测图线，将a图线向

误区三不注意实验数据的前期分析，随意选取数据处理

例3物理小组在一次探究活动中测量滑块与木板之间的动摩擦因数.实验装置如图6，一表面略粗糙的木板固定在水平桌面上，一端装有定滑轮.木板上有一滑块，其一端与电磁打点计时器的纸带相连，另一端通过跨过定滑轮的细线与托盘连接.打点计时器使用的交流电源的频率为50Hz.开始实验时，在托盘中放入适量砝码，滑块开始做匀加速运动，在纸带上打出一系列的点.图7给出的是实验中获取的一条纸带的一部分：O、A、B、C、D、E、F、G是计数点，每相邻两计数点间还有4个打点(图中未标出)，计数点间的距离如图所示.根据图中数据可求得加速度a=________m/s2(保留三位有效数字).

图6

图7

学生解题误区：学生在处理这样的问题时，往往想到的是用逐差法求解如下：

对策：在实验数据的处理上，应使学生养成良好的分析数据的习惯，及时剔除因过失等原因形成的问题数据，为正确处理实验数据打下坚实的基础.对本例来说，应先根据匀变速直线运动规律：ΔS=S2-S1=S3-S2=…=aT2，进行数据分析，去掉S1=3.18cm这一问题数据，然后再根据逐差法求出加速度a=0.801m/s2.

上述所列都是学生在运用数学方法解决相关实验问题时，易犯的几种典型错误，有必要加以分析总结，研究其对策.实验数据有其产生的物理条件，也有其遵循的物理规律，所以这绝不是一个单纯的数学问题，教师要通过教学，让学生形成一种观念：我们要灵活、合理、正确地运用数学方法解决物理问题.

参考文献：

费业泰.误差理论与数据处理[M].北京：机械工业出版社，2010.

·名师论坛·