双旋翼直升机旋翼的微多普勒特性分析*

陈鹏，郝士琦，胡以华，李政

（1.脉冲功率激光技术国家重点实验室，合肥230037；2.电子工程学院，合肥230037）

双旋翼直升机旋翼的微多普勒特性分析*

陈鹏1，2，郝士琦1，2，胡以华1，2，李政1，2

（1.脉冲功率激光技术国家重点实验室，合肥230037；2.电子工程学院，合肥230037）

目前，国内外对双旋翼直升机的微多普勒特性研究相对还很少。建立了直升机旋翼回波的微多普勒模型，并基于该模型，分别计算了共轴式、横列式、纵列式以及交叉式双旋翼直升机的微多普勒。研究结果表明，不同种类的双旋翼直升机旋翼的微多普勒特性不同，通过对双旋翼直升机旋翼的微多普勒进行分析，可以对双旋翼直升机进行初步分类，为下一步双旋翼直升机的微多普勒识别提供了参考和借鉴。

微多普勒，双旋翼直升机，分析识别

0 引言

目标的微动特征是指目标或目标部分结构的振动、旋转等小幅的非刚体运动［1-3］。目标的这种微小运动会在雷达回波中引入一个频率调制，并会在目标的多普勒频率偏移上产生一个边带，对于这种由于微小运动产生的调制称为微多普勒现象（micro-doppler，MD）［1-5］。近年来，学者们将微多普勒技术与雷达目标识别结合，发展了基于微多普勒分析的目标识别技术［6］，为目标识别提供了新方法、新思路。

一直以来，国内外学者对直升机目标的微多普勒研究十分关注。Victor C Chen教授提出了微多普勒这个概念，深入研究了微多普勒的产生原理，并建立了微动的数学模型［2］。王维研究了直升机旋转部件的物理特性及雷达回波的微多普勒［6］。双旋翼直升机包括共轴式直升机、横列式直升机、纵列式直升机和交叉式直升机等。目前双旋翼直升机旋翼特征对微多普勒影响研究在国内外开展的工作还较少。

本文构建了双直升机旋翼的探测回波模型，并基于该模型，分别对共轴式、横列式、纵列式和交叉式双旋翼直升机旋翼的微多普勒进行了仿真和数值分析，为双旋翼直升机旋翼微多普勒的目标特征参数的选取提供依据。

1 探测回波模型

1.1 距离单元模型

图1为雷达与旋翼的位置关系示意图，其中旋翼上点P到接收机的距离Rp为：

式中，R0为旋翼中心到雷达的距离，lp为旋翼上P点到旋翼中心的距离，φ0为旋翼的初始相位角，Ω为旋翼转速。

图1 雷达与旋翼的位置关系

旋翼的回波信号可表示为［7］：

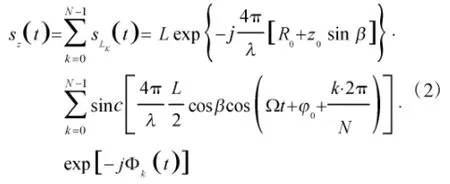
1.2 微多普勒分析

在回波信号中，相位信息决定信号的瞬时频率，旋翼中第k个叶片的微多普勒频率fD，k可以从对式（4）中的Φk（t）求导得出，即：

使用窄窗函数的傅里叶变换习惯称为短时傅里叶变换（STFT），它是加窗傅里叶变换的一种形式。加窗傅里叶变换最早由Gabor于1946年提出［8］。给定一个时间宽度很短的窗函数η（t），让窗滑动，则信号z（t）的短时傅里叶变换（STFT）定义为［9］：

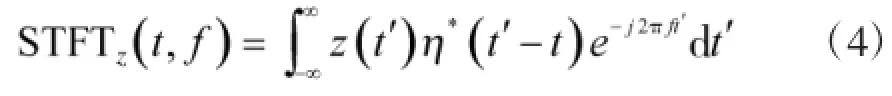
2 仿真与分析

2.1 双旋翼共轴式直升机

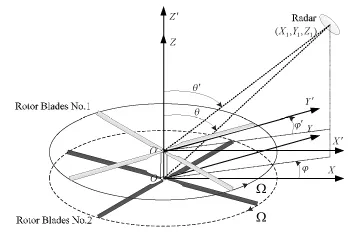
图2 共轴式直升机旋翼位置

如图2所示，共轴式直升机的特点是两个旋翼上下排列，在同一轴线上反向旋转，如×××型武装直升机。×××型直升机旋翼直径14.43m，两旋翼中心距离为1 m，设雷达位置为（x=1 000 m，y=0 m，z= 1 000 m），旋翼位置为（x=0 m，y=0 m，z=0 m），载波频率f0=5 GHz，叶片数N=4，叶片长度a=7.215 m，叶片宽度W=0.2 m，转速Ω1=4×2πrad/s，根据式（1），对叶片旋翼的微多普勒进行仿真，结果如图3所示。

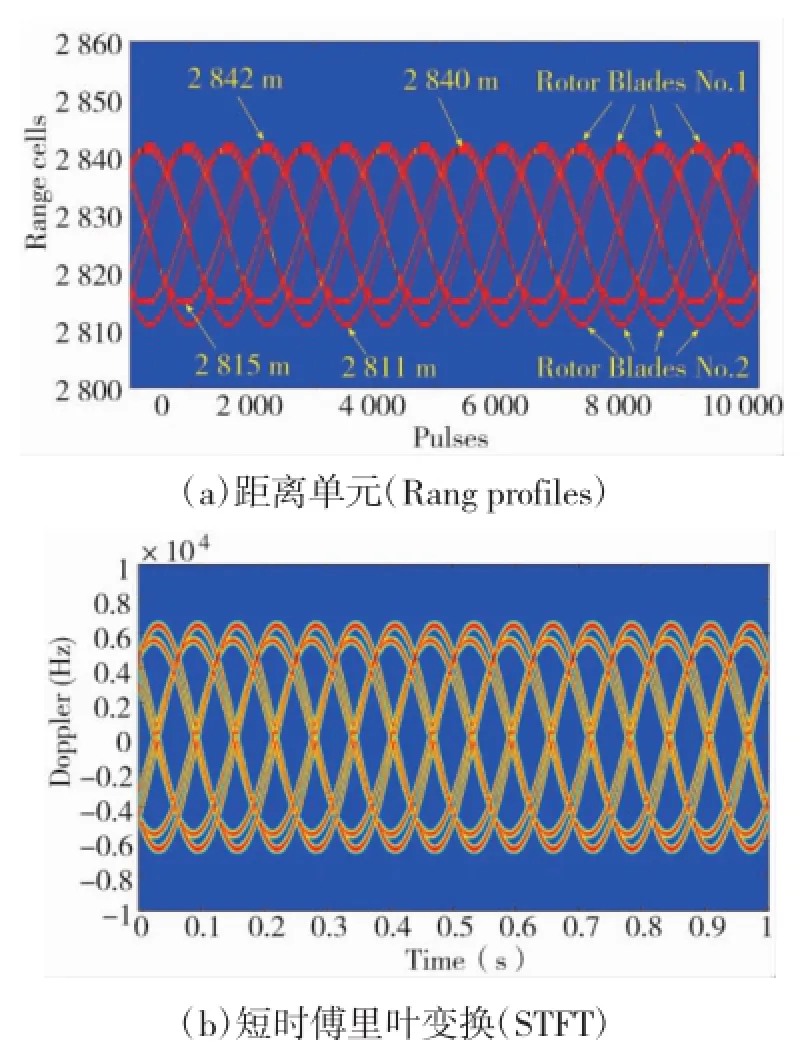
图3 共轴式直升机旋翼微多普勒

由图3（a）可知，双旋翼共轴式直升机旋翼距离单元是由8条类正弦曲线组成，其中4条曲线形状相似且相位差相同，最大值为2 842 m，最小值为2 815 m是Rotor Blades No.1的距离单元，另外4条曲线形状相似且相位差相同，最大值为2 840 m，最小值为2 811 m是Rotor Blades No.2的距离单元，6条曲线周期相同，曲线最大值相差约为2 m，最小值相差4 m。由图3（b）可知，直升机旋翼的微多普勒由两部分组成。

2.2 双旋翼横列式直升机

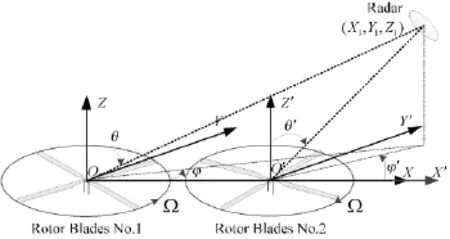
图4 横列式直升机旋翼位置

如图4所示，两个旋翼左右横向排列，轴间距较远，旋转方向相反，如×××型军用运输直升机。×××型军用运输直升机旋翼直径14 m，机身长度17.5 m，两旋翼中心距离为14 m，设雷达位置为（X=1 000 m，Y=0 m，Z=1 000 m），旋翼位置为（x=0，y=0，z=0），载波频率f0=5 GHz，叶片数N=3，叶片长度a=7 m，叶片宽度W=0.2 m，转速Ω1=4×2πrad/s，根据式（1），对叶片旋翼的微多普勒进行仿真，仿真结果如图5所示。

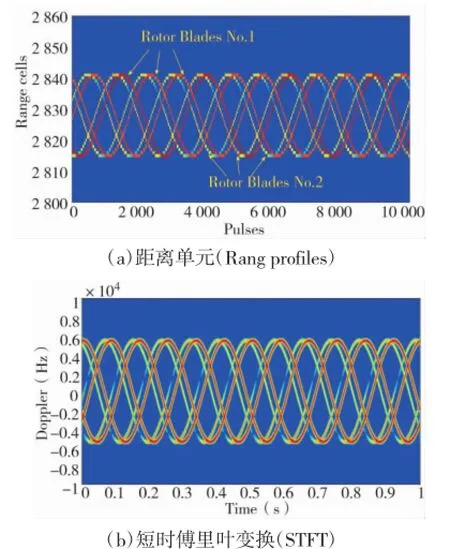
图5 横列式直升机旋翼微多普勒

由图5（a）可知，双旋翼横列式直升机旋翼距离单元是由6条类正弦曲线组成，其中3条曲线形状相似且相位差相同为Rotor Blades No.1的距离单元，另外3条曲线为Rotor Blades No.2的距离单元，6条曲线周期相同，幅度相同，两个旋翼中心距离几乎相等。由图5（b）可知，直升机旋翼的微多普勒由形状相似的两部分组成。

2.3 双旋翼纵列式直升机

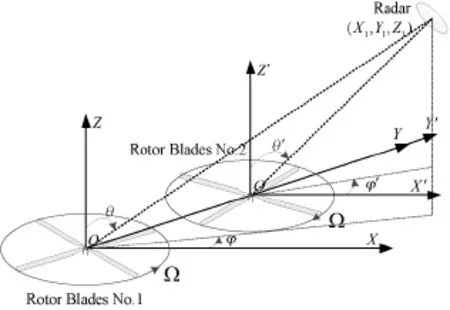
图6 纵列式直升机旋翼位置

如图6所示，两个旋翼前后排列，旋转方向相反，多见于大型直升机，如×××型军用运输直升机。×××型军用运输直升机旋翼直径18.8 m，机身长度17.5 m，两旋翼中心距离为15.54 m，设雷达位置为（X=1 000 m，Y=0，Z=1 000 m），旋翼位置为（x=0，y=0，z=0），载波频率f0=5 GHz，叶片数N=3，叶片长度a=7 m，叶片宽度W=0.2 m，转速Ω1=4× 2πrad/s，根据式（1），对叶片旋翼的微多普勒进行仿真，仿真结果如图7所示。

图7 纵列式直升机旋翼微多普勒

由图7（a）可知，双旋翼纵列式直升机如图是由6条类正弦曲线组成，其中3条曲线形状相似，相位差相同且曲线中心约为2 828 m是Rotor Blades No.1的距离单元，另外3条曲线形状相似，相位差相同且曲线中心约为2 806 m是Rotor Blades No.2的距离单元，6条曲线周期相同，幅度相同，两个旋翼中心距离几乎相等。由图7（b）可知，直升机旋翼的微多普勒由形状相似的两部分组成。

2.4双旋翼交叉式直升机

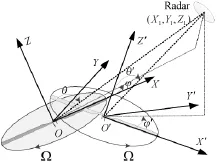
图8 交叉式直升机旋翼位置

如图8所示，两个旋翼左右横向排列，旋翼轴间距较小，并且不平行，旋转方向相反，如×××型中型起重调运直升机。×××型中型起重调运直升机旋翼直径14.73 m，机身长度15.85 m，两旋翼中心距离为3 m，旋翼倾角分别为20°和-20°，设雷达位置为（X=1 000 m，Y=0，Z=1 000 m），旋翼位置为（x=0，y=0，z=0），载波频率f0=5 GHz，叶片数N=2，叶片长度a=7 m，叶片宽度W=0.2 m，转速Ω1=4× 2πrad/s，根据式（1），对叶片旋翼的微多普勒进行仿真，仿真结果如图9所示。

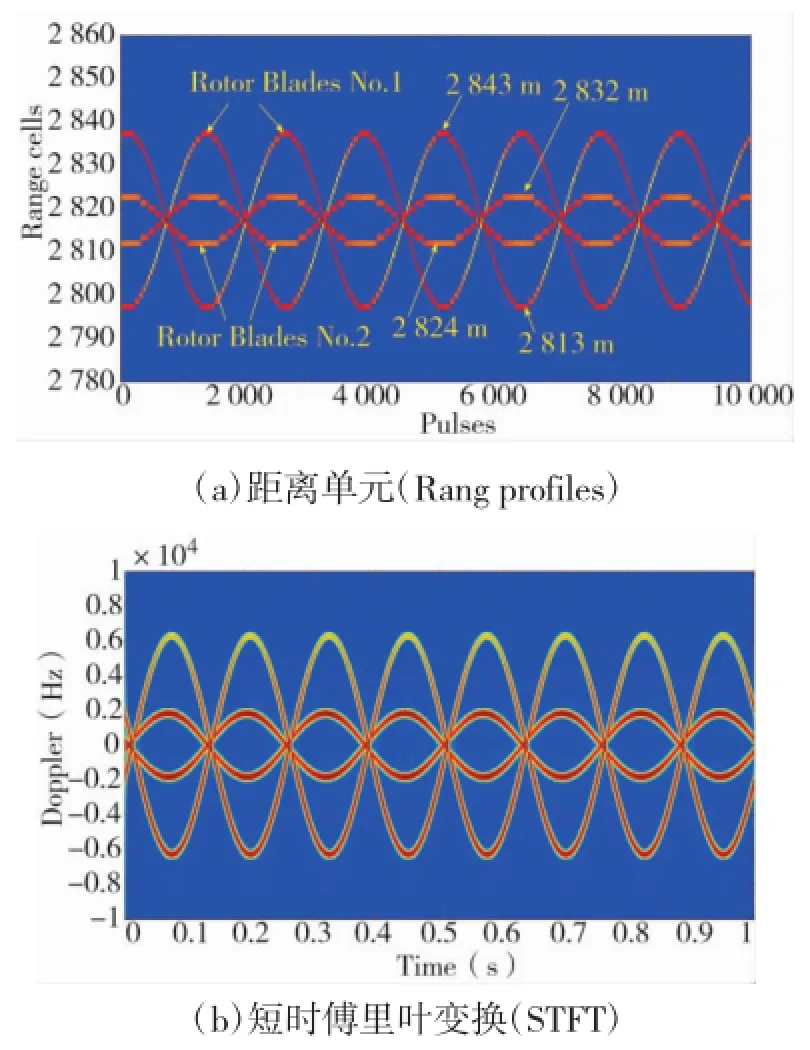
图9 交叉式直升机旋翼微多普勒

由图9（a）可知，双旋翼纵列式直升机是由4条类正弦曲线组成，其中2条曲线形状相似，相位差相同，最大值为2 843 m，最小值为2 813 m是Rotor Blades No.1的距离单元，另外两条曲线形状相似，相位差相同，最大值为2 832 m，最小值为2 824 m是Rotor Blades No.2的距离单元，6条曲线周期相同，幅度相同，两个旋翼中心距离几乎相等。由图9（b）可知，直升机旋翼的微多普勒由4条类正弦曲线组成，其中幅度较大的为Rotor Blades No.1的微多普勒，幅度较小的为Rotor Blades No.2的微多普勒。

3 结论

本文建立了直升机旋翼的距离单元模型，并基于该模型分别对共轴式、横列式、纵列式、交叉式双旋翼直升机的旋翼回波进行了仿真，利用短时傅里叶方法（STFT）对仿真数据进行了微多普勒分析。

研究结果表明：不同种类的双旋翼直升机探测回波不同，微多普勒特征亦不同。共轴式直升机的各旋翼回波曲线振幅不同，周期大致相同，微多普勒曲线的振幅有明显差别。横列式直升机的各旋翼回波曲线的相位明显不同，微多普勒曲线的相位有明显差别。纵列式直升机的各旋翼回波的曲线中心明显不同，虽然微多普勒曲线的重叠度较高，但是仍可看出由两部分组成。交叉式直升机的各旋翼回波的振幅明显不同，微多普勒曲线的振幅也有明显区别。

综上所述，通过分析双旋翼直升机的微多普勒可以初步判断双旋翼直升机的种类，为双旋翼直升机的微多普勒探测提供了参考和借鉴。

［1］Chen V C，Li F Y，Ho S S，et al.Micro-Doppler Effect in Radar:Phenomenon，Model，and Simulation Study［J］.IEEE Transactions on Aerospace and Electronic Systems，2006，42（1）:2-21.

［2］Chen V C.Analysis of Radar Micro-Doppler Signature with Time-Frequency Transform［C］//Proc Statistical Signal and Array Processing.Pocono Manor，PA，USA:IEEE Press，2000:463-466.

［3］Chen V C，Li F Y.Analysis of Micro-Doppler Signatures［J］. IEE Proc Radar Sonar navig，2003，150（4）:271-276.

［4］Chen V C.Time-Frequency Signatures of Micro-Doppler Phenomenon for Feature Extraction［C］//Proceedings of SPIE in Wavelet Applications VII.Orlando，USA，SPIE press，2000:220-226.

［5］Sparr T，Krane B.Micro-Doppler Analysis of Vibrating Targets in SAR［J］.IEE，2003，150（4）:277-283.

［6］王维.基于微多普勒特征的空中目标识别技术研究［D］.南京:南京信息工程大学，2012.

［7］Chen V C.The Micro-Doppler Effect in Radar［M］.Boston：Artech House，2011.

［8］GaborD.Theoryofcommumication［J］.IEE，1946，93: 429-457.

［9］葛哲学，陈仲生.Matlab时频分析技术及其应用［M］.北京:人民邮电出版社，2005.

Micro-Doppler Analysis of a Double-blade Helicopter’s Rotor Blades

CHEN Peng1，2，HAO Shi-qi1，2，HU Yi-Hua1，2，LI Zheng1，2
（1.State Key Laboratory of Pulsed Power Laser Technology，Hefei 230037，China；
2.Electronic Engineering Institute，Hefei 230037，China）

At present，the study of micro-doppler of a double-blade helicopter’s rotor blades at home and abroad is lack.In this paper，a micro-doppler model of a helicopter rotor is established. Based on the model，the micro-doppler of coaxial helicopter’s rotor blades，horizontal-modal helicopter’s rotor blades，tandem helicopter’s rotor blades and cross-modal helicopter’s rotor blades is calculated.The results show that the micro-doppler of different type of double-blade helicopter’s rotor blades is different，and the type of a double-blade helicopter can be classified primarily through analyzing the micro-doppler of a double-blade helicopter’s blades，which provided some reference for double-blade helicopter identification by micro-doppler.

micro-doppler，double-blade helicopter，analysis and identification

TN95

A

1002-0640（2015）02-0009-04

2013-12-21

2014-02-04

国家自然科学基金资助项目（61271353）

陈鹏（1988-），男，北京人，硕士研究生。研究方向：激光探测方面的研究工作。