GCr15轴承钢剪切分析韧性断裂准则的适用性研究

胡宾，郝南海

(北京信息科技大学 机电工程学院，北京 100192)



GCr15轴承钢剪切分析韧性断裂准则的适用性研究

胡宾，郝南海

(北京信息科技大学 机电工程学院，北京 100192)

摘要：运用DEFORM有限元软件，采用试验与有限元模拟相结合的方法，对DEFORM内嵌的几个断裂准则在GCr15轴承钢板料剪切成形中的适用性进行了研究分析，发现所研究的8个准则均不能直接用于准确预测GCr15轴承钢板料剪切断面的光亮带高度。为此，提出了一种修正阀值、分段拟合的模拟方法，使所研究的断裂准则在阀值修正之后能够较为准确地预测GCr15剪切断面光亮带的实际高度。

关键词：板料剪切；断裂准则；分段模拟

0引言

在滚动轴承的生产中，内外圈可采用GCr15无缝钢管直接剪切得到。相比传统的生产方法，这种剪切加工无材料损失，生产效率高。但是，现今对GCr15轴承钢的剪切研究依然甚少，尚未明确适用于该材料剪切断裂的韧性断裂准则。

板料冲裁变形的过程大致可分为弹性变形、塑性变形和断裂分离3个阶段。

1) 弹性变形阶段

在弹性变形阶段，板料发生弹性压缩和弯曲，材料内的应力尚未达到弹性极限。

2) 塑性变形阶段

当板料的应力达到屈服极限，冲裁就由弹性变形阶段进入到塑性变形阶段。凸模切入板料，板料被挤入凹模洞口。在剪切面的边缘，由于凸-凹模间隙存在而引起的弯曲和拉伸作用，形成塌角面，同时由于剪切变形，在切断面上形成光亮且与板面垂直的断面。

3) 断裂分离阶段

当板料的应力达到抗剪强度后，凸模继续下压，凸、凹模刃口附近产生微裂纹不断向板料内部扩展。当上下裂纹重合时，板料便实现了分离。由于拉断结果，断面上形成一个粗糙的区域。凸模继续下行，已分离的材料克服摩擦阻力，从板料中推出，完成整个冲裁过程。

板料断裂面的品质直接影响零部件的表面品质，剪切断面一般会较明显地分成四个特征区，即塌角带、光亮带、撕裂带和毛刺。其中光亮带是剪切面上粗糙度最低，精度最高的部分。

根据现有理论，同一种材料，对断面品质起决定作用的是冲裁间隙(即本文所述的“剪切间隙”)。在相同的剪切条件下，光亮带的高度会随着剪切间隙的变化而变化。

本文将通过实际试验和DEFORM有限元软件模拟相结合的方法，将有限元模拟得到的光亮带高度与实际试验值进行比较，分析Normalized C&L、McClintock、Freudenthal等共计8个韧性断裂准在GCr15板料剪切中的适用性。

1DEFORM内嵌的韧性断裂准则简介

利用DEFORM对GCr15板料剪切成形过程进行有限元模拟。模拟在DEFORM内嵌的8个断裂准则下进行，以下列出它们的阀值计算公式。

1) Normalized C&L 准则

(1)

σ*——材料拉伸时的最大拉应力，即第一主应力；

C——阀值。

2) Cockcroft & Latham 准则:

(2)

3) McClintock 准则

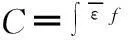
(3)

式中：n——材料的硬化系数；

σa——材料拉伸时的最小主应力；

σb——材料拉伸时的最大主应力。

4) Freudenthal 准则

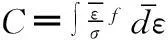
(4)

5) Rice & Tracy 准则

(5)

式中：α——材料试验参数，视不同的加载情况取值；

σm——静水应力。

6) Ayada 准则

(6)

7) Brozzo 准则

(7)

8) Zhao & Kuhn 准则

(8)

2GCr15板料剪切的DEFORM模拟

2.1　所需材料特性参数的求取

a) GCr15棒料拉伸试验

拉伸试验所用GCr15棒料的尺寸为直径10mm，标距(有效拉伸段原始长度)100mm，如图1所示。

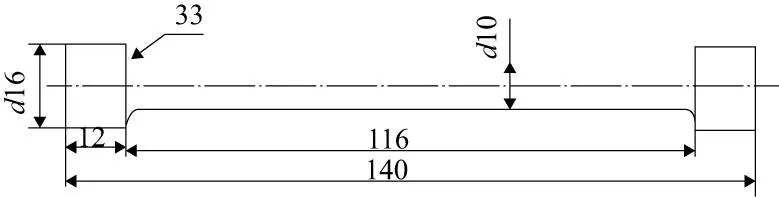
图1　拉伸试验所用的GCr15棒料

棒料被拉断后，测得其断裂面(缩颈处)直径为6.6mm，最大名义应变εmax发生的缩颈处，即：

(9)

式中：l0、d0、A0——棒料拉伸前的标定长度、横截面直径和面积；

l、d、A——棒料拉升后的标定长度、断裂面直径和面积。

经换算，可得相应的真实应变为：

(10)

即式(1)-式(7)中，有：

(11)

b) GCr15棒料压缩试验

压缩试验所用GCr15棒料的尺寸为直径16mm，长度30mm，如图2所示。

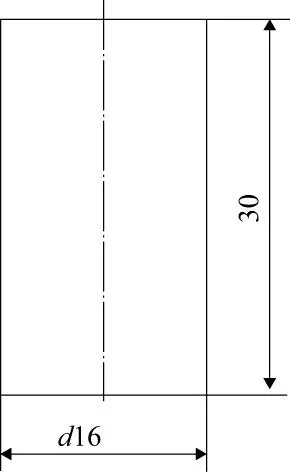
图2　压缩试验所用的GCr15棒料

试验得到的位移-压力曲线如图3所示。

图3　压缩试验位移-压力曲线

根据以下真应力、真应变计算公式：

真应力：

σT=σ(ε+1)

(12)

真应变：

εt=ln(1+ε)

(13)

将该位移-压力曲线换算成真应力-应变曲线，如图4所示。

图4　GCr15棒料真应力-应变曲线

对真应力-应变曲线进行拟合，得到其回归方程：

σ=Kεn-1043ε0.198(MPa)

(14)

式中：K——强度系数，经测算，K-1043；

n——应变硬化指数，经测算，n=0.198。

由于是单向拉伸，故有：

(15)

将式(11)、式(14)和式(15)分别代入式(1)-式(8)，可得各断裂准则的阀值，如表1所示。

表1　各韧性断裂准则的阀值

2.2　DEFORM模拟

在DEFORM中，考虑到对称性，剪切板料及上下模都取原来的1/4，如图5。在前处理中，权衡计算速度和计算精度，取有限元网格数为30000，细化剪切刃口处的网格，细化比率设置为0.01。设置模拟步长为0.02 mm，模拟步数为500。将表1中的阀值输入DEFORM各相应的断裂准则，模拟得到在不同剪切间隙、不同断裂准则下，剪切断裂面光亮带高度的模拟值。

图5　GCr15板料在DEFORM下的剪切模型

3GCr15板料的实际剪切试验

实际剪切试验所用的板料长60mm，宽18mm，厚5mm，如图6所示。

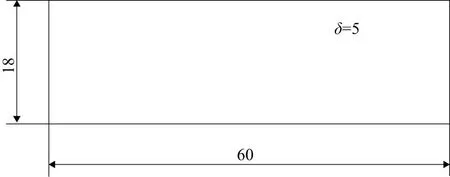
图6　实际剪切试验所用的GCr15板料

针对这一试验，设计了如图7所示的剪切装置。本试验分别采用8个不同直径的冲头来进行板料的剪切，板料的单边剪切间隙分别为0.15mm、0.30mm、0.45mm、0.60mm、0.75mm、0.90mm、1.05mm和1.20mm，间隙相对板料厚度的百分比为3%、6%、9%、12%、15%、18%、21%和24%。

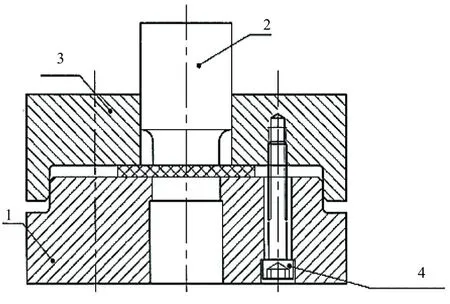
图7　GCr15板料剪切试验装置

4模拟与试验结果的比较与处理

将表1中的阀值输入DEFORM中各相应的断裂准则，模拟得到在不同剪切间隙、不同断裂准则下，剪切面光亮带高度的模拟值，如表2所示。

表2 GCr15 板料光亮带高度的DEFORM模拟值　　　　mm

GCr15板料剪切试验中，板料被剪成三段，取非落料的两段为样本，分别标记为样本1和样本2，测量光亮带高度，并以该两测量值的平均值作为试验典型值，得到的结果如表3所示。

表3　GCr15板料光亮带高度的试验值　mm

根据表2和表3，可绘制单侧剪切间隙-光亮带高度折线图，如图8所示。

由图8可知，上述各断裂准则都不能准确反映GCr15板料的剪切间隙和光亮带高度之间的关系。为能较为准确地拟合实际曲线，将采用分段拟合和阀值修正的方法对模拟结果进行处理。

图8　单侧剪切间隙-光亮高度折线图

虽然所研究的8个断裂准则的模拟曲线都不能准确地预测实际的剪切结果，但不同间隙段之间总有至少一段DEFORM模拟的折线段的斜率与实际试验所得折线段相接近，故可以尝试令该模拟折线段上的数值乘以同一权值，使该段折线上下平移，和实际剪切曲线基本重叠，以达到拟合的目的。以间隙0.15~0.30 mm段为例，直观观察可知，Normalized C&L下的模拟折线的斜率在该区间段和实际剪切曲线斜率最为接近，故采用Normalized C&L准则修正拟合。选定该韧性断裂准则后，在DEFORM软件中适当调整断裂准则的阀值C，重复多次模拟，直至模拟结果的光亮带高度与实际结果基本吻合。

经多次反复模拟试验，各段的断裂准则的阀值C调整如表4所示。

表4　GCr15板料剪切模拟的断裂准则阀值的调整

相应地，得到阀值调整后的光亮带高度模拟值，如表5所示。

表5　阀值调整后的GCr15板料光亮带高度模拟值　　　mm

对比表3与表5的数据，可知除了间隙1.05~1.20的DEFORM模拟值和实际试验典型值有较大的偏差之外，其余6个区间段在调整阀值之后，所得到的模拟值与试验典型值均比较接近；而且，即便是误差较大的间隙为1.05~1.20的模拟值，依然控制在试验样本的取值上下限之内。因而可以较为客观地反映GCr15板料剪切的结果。

依据现有理论，决定光亮带对于剪切板料的相对高度Δ/t的最主要因素是板料的剪切间隙Z/2t(%)。本文所述试验所用板料厚度t=5mm，单侧剪切间隙Z/2=0.15~2.0mm，据此可转换表3、表5数据，得到任意厚度GCr15板料的光亮带与剪切间隙之间的对应关系，如表6所示。

表6　GCr15板料光亮带与剪切间隙之间的关系

续表6

根据表6，可绘制出剪切间隙与光亮带之间的关系曲线，如图9所示。

图9　单侧剪切间隙Z/2t(%)光亮带Δ/t折线图

其中，由于各节点处的模拟值既是前一折线段的终值又是后一折线段的起始值，在前后两种不同的断裂准则下模拟得到的数值一般会有微小的偏差，因而会有两个不同的Δ/t值与之相对应。在图8中，DEFORM模拟结果所示的各折线段的节点值取的是这两个不同的Δ/t的平均值。

可见，经处理后得到的DEFORM模拟结果与实际剪切结果极为接近。

5结论

本文在DEFORM有限元软件的8种韧性断裂准则下模拟了GCr15的剪切断裂，并测量、分析了断裂面的光亮带高度。根据与实际剪切试验数据的对比，可知这8种断裂准则均不能直接用于模拟GCr15板料的剪切断面成形，但是，通过调节断裂准则阀值、分段拟合的方法，能较为准确地模拟GCr15板料的断裂面光亮带高度。在以后GCr15管材剪切成形断面质量的预测和分析中，可先计算剪切间隙与管壁厚度的比值(即相当于表6中的剪切间隙Z/2t)，再对比表4，查所适用的韧性断裂准则和相对应的调整后的阀值，最后在DEFORM中模拟，即可预测GCr15管材单向剪切的断裂面光亮带高度。

参考文献:

[1] 周劼实，周贤宾. 成形极限预测韧性断裂准则及屈服准则的影响[J]. 北京航空航天大学学报，2006，32(8)：969-973.

[2] 高付海，桂良进，范子杰. 基于韧性准则的金属板料冲压成形断裂模拟[J]. 工程力学，2010，27(2)：204-208.

[3] 刘向远. 轴承钢管剪切过程有限元分析[D]. 北京：北京信息科技大学，2013.

[4] 翟建军, 等. 板料和型材的冲压与成形技术[M]. 北京：机械工业出版社，2008.

[5] 付宏生. 冷冲压成形工艺与模具设计制造[M]. 北京：化学工业出版社，2005.

[6] 李硕本. 冲压工艺理论与新技术[M]. 北京：机械工业出版社，2002.

[7] 洪慎章. 实用冲压工艺及模具设计[M]. 北京：机械工业出版社，2008.

[8] 张如华. 冲压工艺与模具设计[M]. 北京：清华大学出版社，2006.

Research on Applicability of Ductile Fracture Criteria in Sheet Blanking

HU Bin, HAO Nan-hai

(Beijing Information Science & Technology University, Beijing 100192, China)

Abstract:By means of DEFORM, this essay analyses and a researches on the applicability of ductile fracture criteria in DEFORM in GCr15 sheet blanking, by combining experiments with finite element simulations, and finds out the 8 criteria researched on, which can not be directly used to predict the height of the euphotic belts generated in GCr15 sheet blanking exactly. So it puts forward a new simulation method, which is used to make the criteria predict its height much more precisely by segment-simulation & threshold modification.

Keywords:sheet blanking; ductile fracture criterion; segment-simulation

中图分类号：TG386

文献标志码：A

文章编号：1671-5276(2015)02-0132-05

作者简介：胡宾(1986-)，男，浙江台州人，硕士研究生，研究方向为机械制造。

收稿日期：2014-06-03 2014-11-04