抽水蓄能发电电动机三维瞬态涡流场有限元分析

张宇娇,秦威南,2,董晓虎,郑 永

(1.三峡大学 电气与新能源学院,湖北 宜昌 443002；2.国网浙江省电力公司 金华供电公司,浙江 金华 321001；3. 中国南方电网 调峰调频发电公司检修试验中心,广州 511400；4.国网新源湖北白莲河抽水蓄能有限公司 运维检修部,湖北 黄冈 438600)

抽水蓄能发电电动机三维瞬态涡流场有限元分析

张宇娇1,秦威南1,2,董晓虎3,郑 永4

(1.三峡大学 电气与新能源学院,湖北 宜昌 443002；2.国网浙江省电力公司 金华供电公司,浙江 金华 321001；3. 中国南方电网 调峰调频发电公司检修试验中心,广州 511400；4.国网新源湖北白莲河抽水蓄能有限公司 运维检修部,湖北 黄冈 438600)

对广州抽水蓄能B厂某发电电动机进行了三维涡流场有限元计算,建立了发电电动机的三维模型,分析了电流密度、磁密等场量的分布情况,获得了气隙径向磁密并进行了谐波分析。通过发电电动机的三维瞬态涡流场计算,可以更加准确地得到电机电磁场分布情况,运算结果能够为电机的设计、选型、国产化制造提供相应参考,在电机优化设计方面具有一定的参考价值。

抽水蓄能;发电电动机;有限元法;瞬态涡流场分析;三维计算

抽水蓄能电站能够利用电力负荷低谷时系统多余的电能将下游的水抽至上水库储存起来,在电力负荷高峰期放水至下水库发电,起到“削峰填谷”和事故备用的作用[1]。它具有的启停迅速、机动性能好、调节能力强以及适用于承担电力系统尖峰负荷和作为紧急备用电源等特点,为电力系统的安全稳定及经济运行提供了重要保障[2-3]。

作为抽水蓄能电站的核心部分,发电电动机在整个电站的安全生产中起着重要作用,其性能优劣、适应程度,直接关系到电站乃至整个电网的安全稳定运行,对电站及电网有着很大影响。

基于发电电动机的运行特点,其制造难度较常规水轮发电机更大,在实际运行中出现的事故率更高[5]。目前国内主要使用阿尔斯通、西门子、东芝、日立等国外公司生产发电电动机,国内方面东电和哈电通过技贸结合的方式也参与制造了如黑麋峰、白莲河等抽水蓄能电站的发电电动机,分别独立制造了仙游和响水涧机组,有了一定的技术积累,但与发达国家相比仍有一定差距[6]。

发电电动机运行期间涉及的电磁、机械、散热等问题十分复杂,是一个多物理场耦合分析问题,有限元法是解决这一问题的有效方法。对于常规电机,各国电机界专家进行了大量研究,积累了丰富经验,目前已初步建立起一套较为系统的数值计算理论与方法,一定程度上解决了以往基于经验公式所得解精度不够的问题,给实际生产中的电机制造、运行维护、检修提供了理论指导,取得了不错的实践效果[7-8]。然而,针对抽水蓄能可逆式发电电动机的电磁、发热、机械强度以及优化设计的研究较少。主要原因是抽水蓄能发电电动机的运行工况复杂,较之常规水轮发电机更难分析。

笔者对广州抽水蓄能B厂某大型复杂结构三相发电电动机进行了三维瞬态涡流场有限元分析计算。建立了电机三维有限元模型,给出了定子绕组和转子励磁绕组电流密度分布、电机整体矢量磁密分布并进行了分析说明,提取了气隙磁密结果并进行了谐波分析。分析表明,三维电磁场有限元计算结果与该发电电动机的电磁设计性能接近,运算结果能够为电机的设计、选型提供相应参考,在电机优化设计和国产化制造方面具有一定的参考价值。

1 发电电动机三维电磁场有限元计算

1.1 三维涡流场的控制方程

根据微分形式下的麦克斯韦方程组推导的以位函数为求解变量的A,φ-A法是一种普遍适用于涡流场有限元计算的方法,具有源电流项易处理、适用于多连域导体和求解精度高的优点。通过将所研究场域分离为涡流区和非涡流区以方便求解。对本发电电动机而言,定子绕组、转子阻尼绕组为涡流区,对电场和磁场都需要计算,即同时采用标量电位φ和矢量磁位A来描述;励磁绕组(视为绞线圈)、铁心(可视为导磁不导电材料[9])、空气为非涡流区,只需计算磁场,用A来描述。发电电动机各部分控制方程如下[9]:

定子绕组、阻尼绕组涡流区:

-jσωA-σ×φ，

(1)

励磁绕组含源非涡流区:

(2)

铁心、空气非涡流区:

.

(3)

式中：μ代表磁导率,H/m;A代表矢量磁位,Wb/m;σ代表电导率,S/m;ω代表角频率,rad/s;φ代表标量电位,V。

式(1)～式(3)中的矢量磁位A通过磁密B=×A引入,控制方程中包含了库仑规范:×A=0.

1.2 发电电动机三维模型

该发电电动机基本参数如表1所示,主要部件包含:定子铁心、定子绕组、转子磁轭、转子磁极、阻尼绕组、励磁绕组。其中定子铁心、转子磁轭和磁极为铁心材料,是构成导磁回路的主要部分;定子绕组和励磁绕组是通入电流并产生磁场的源区;阻尼绕组是由阻尼条通过端环短接构成的,其作用是在发电电动机因负载变化,定子绕组内的电压电流会形成震荡时起增加阻力,形成阻尼震荡,起到一定的缓冲作用。

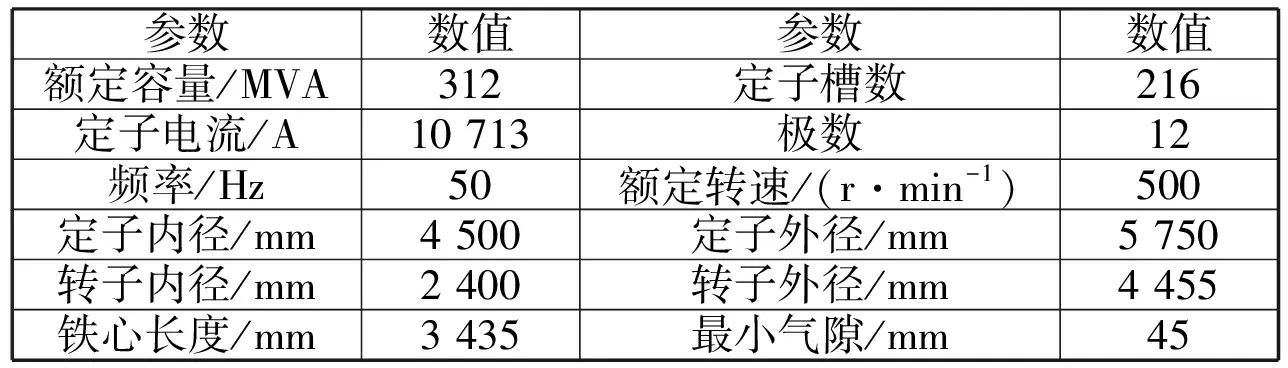
表1 发电电动机基本参数

为了减少计算量,根据电机的结构和磁场分布呈周期性对称特性,求解模型可减少为一对磁极情况，如图1所示。

1.3 本构关系

定子绕组通入交流电后,其电流分布趋向表面集中,产生了趋肤效应。绕组之间彼此距离较近,绕组中电流产生的磁场会导致其相邻绕组中的电流分布更加不均匀,称之为邻近效应。由于趋肤效应和邻近效应的影响,电流流过导体的有效截面减少,电阻相应增大。实际计算中通过引入费立德系数KF来等效计及交流电阻的增加,由于该电机绕组为单根矩形绕组,一个槽中含有上下两层绕组,趋肤效应和邻近效应较明显,因此取1.33做极端情况考虑。另外,为了减少网格剖分难度和计算量,剖分时将绝缘材料并入绕组导体部分,不对其进行剖分,以KE为等效系数,用于考虑绝缘对电阻率的影响,取1.4[10]。

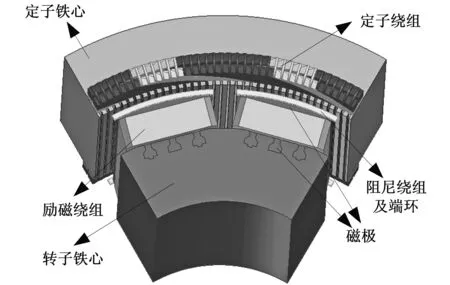
图1 发电电动机1/6周期模型Fig.1 Generator-Motor 1/6 Cycle Model

不考虑温度对电阻率的影响,认为电阻率为恒定值。由于铁心材料由电工硅钢片制成,电阻率很高,为了方便计算,因此设置为导磁不导电材料,不考虑磁滞损耗。磁导率为各项同性,铁磁材料磁化曲线如图2所示。以有效磁导率来等效考虑铁磁材料磁导率的非线性影响[11]:

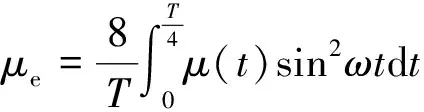
(4)

式中：T为周期(s)；μe为有效磁导率；μ(t)为瞬时磁导率。工程中以下式进行相对磁导率的计算:

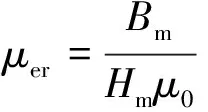
(5)

式中：μ0为真空中的磁导率4π×10-7H/m；对于该发电电动机铁心材料,Bm取1.143 T；Hm取200 A/m。发电电动机各部件材料属性如表2所示。

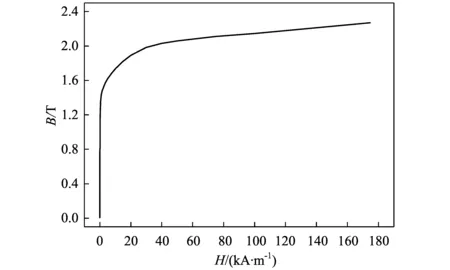
图2 电机铁磁材料磁化曲线Fig.2 Magnetization Curve of Ferromagnetic Material

表2 发电电动机各部件材料属性

1.4 媒质分界面条件

电机中存在着许多不同磁媒质分界面,如励磁绕组与磁极、阻尼绕组与磁极、定子绕组与定子铁心等。在这些不同磁媒质分界面上存在着磁化面电流,造成分界面两侧场矢量不连续。为满足分界面上的电磁连续条件和规范约束,要求分界面上矢量磁位A的函数连续并且法向导数也连续。

1.5 边界条件及网格剖分

由于采用了1/6周期模型来求解,因此需要对电机赋予周期性边界条件。周期性边界条件反映的是如何利用边界条件替代所选电机周期模型受到其余未建模型的影响。如果去掉其余模型,保持该电机周期模型计算结果不变应该附加的条件,将具有时空周期性的问题简化为一个周期单元模型进行处理,使电机周期边界处具有相同大小、方向的场量。定子铁心磁导率很高,可认为磁力线在定子铁心外边界处满足磁力线平行边界条件。

图3 电机网格剖分图Fig.3 Motor Mesh Subdivision Graph

图3为发电电动机的1/6模型剖分图,为了清楚的展示剖分结果,空气部分剖分仅显示了气隙带部分。剖分单元采用四面体单元,具有几何特征简单、描述能力强的特点,适合于形状复杂模型的网格剖分。气隙、阻尼绕组和定子绕组为重点关注区域,剖分控制相对较密,以保证足够的计算精度。模型一共有2 344 094个单元。

1.6 施加载荷及求解方法

该发电电动机有12个磁极,每极每相槽数为6,每槽分为上下两层绕组,绕组以波绕组形式连接,第一节距为16,第二节距为20,并联支路数为4.对1/6周期模型中的定子绕组施加三相交流电流,幅值大小为3 787.62 A,A、B、C三相电流相位依次相差120°.瞬态场中转子额定旋转速度为500 r/min,励磁绕组通入直流电流72 480 A。计算时长取一个电周期20 ms.

采取不完全共轭梯度迭代算法(ICCG,The Incomplete Cholesky Conjugate Gradient)对模型求解。该方法适用于静态、涡流和时谐场分析,所需迭代次数少,收敛快,只需储存非零元素,大大减少了计算对内存的需求,能够求解对称、非对称矩阵、复杂矩阵、正定矩阵、不定矩阵,非常适合于求解大规模有限元方程。

2 计算结果及分析

2.1 电流密度分布

图4为20 ms时定子绕组的电流密度云图,由于趋肤效应,电流在导体中分布式不均匀分布的,可以看到此时A相电流最大,B、C相电流大小为A相的一半。对于A相,电密幅值为2.67×106A/m2,乘以绕组截面积得电流幅值大小为3 972.832 A,与加载的电流幅值3 787.62 A有所差别,这是因为趋肤效应使得导体表面的电流密度分布不均匀,局部增大了的缘故。图5为A相单根定子绕组中电流矢量分布图,从中可以清楚地看到电流的流向,与加载方向一致。由于铁心设置为导磁不导电材料,因此铁心中没有电流。

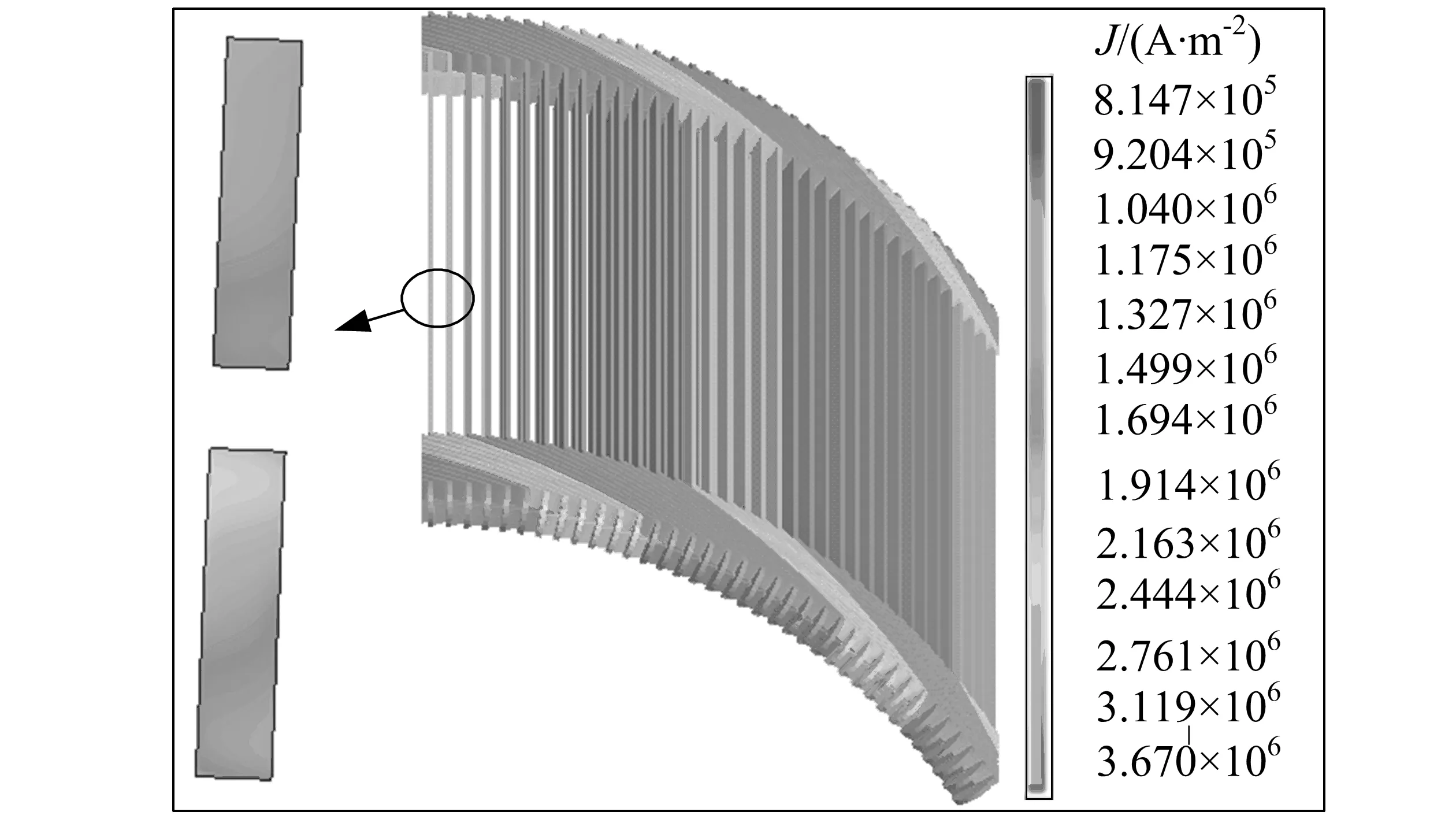
图4 定子绕组电流密度(20 ms时刻)Fig.4 Current Density of Stator Winding

该发电电动机励磁绕组通入的励磁电流为直流电,匝数为32匝,可以视为绞线圈模型,求解后的电流密度矢量如图6所示,励磁电流密度最大值为3.05×106A/m2,乘以励磁绕组截面积得总电流为72 480.6 A,与所加载的72 480 A非常接近。以上计算结果说明定子绕组电流和励磁绕组电流的加载是正确的。

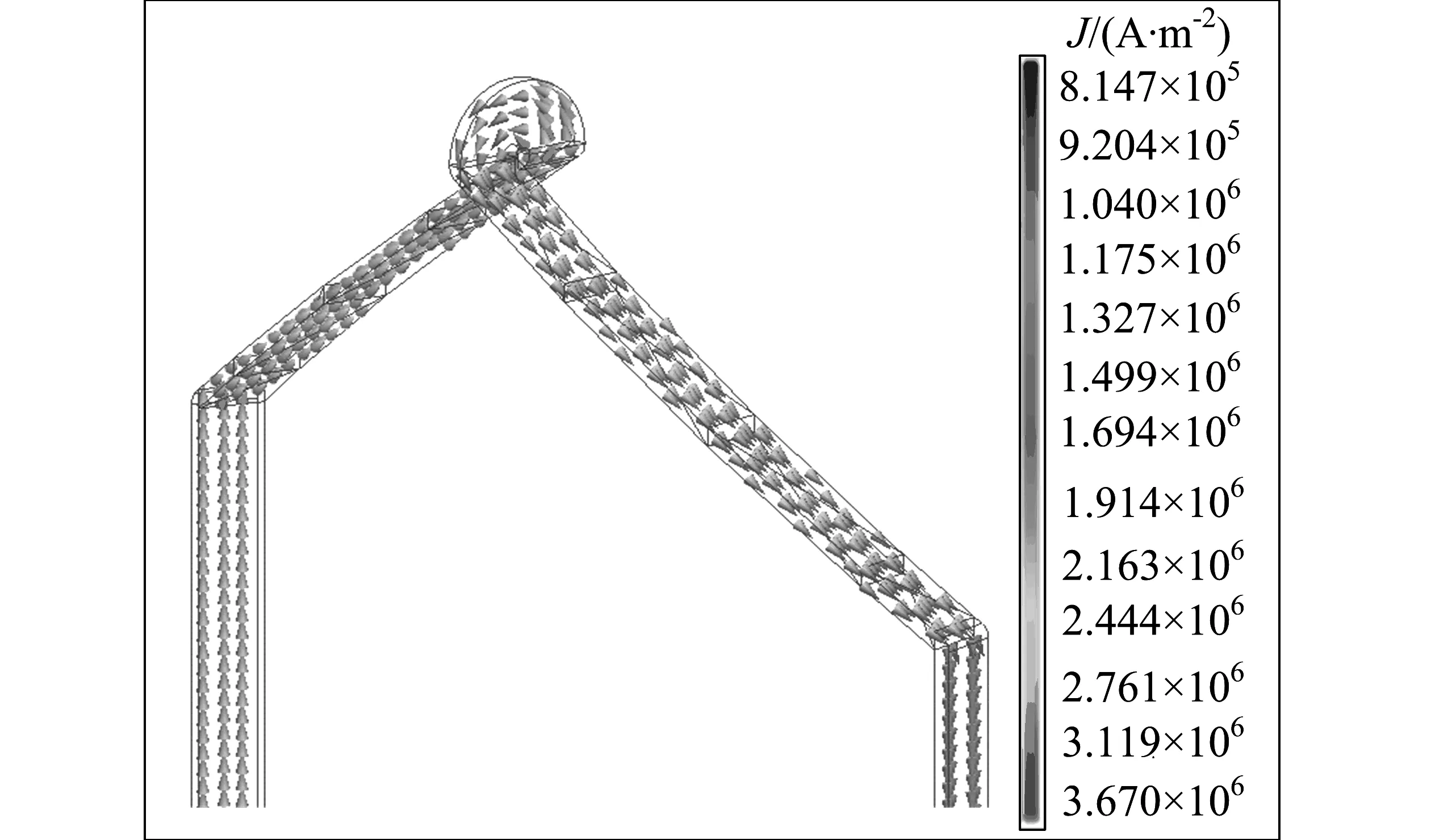
图5 定子A相单根绕组电流密度矢量图(20 ms时刻)Fig.5 Current Vector Distribution of Single Conductor in the Stator Windings of Phase A

图6 励磁绕组电流密度矢量图(20 ms时刻)Fig.6 Current Density Vector in the Excitation Winding

图7为转子阻尼绕组上感应电流的矢量分布图,最大电流密度为1.499×106A/m2。

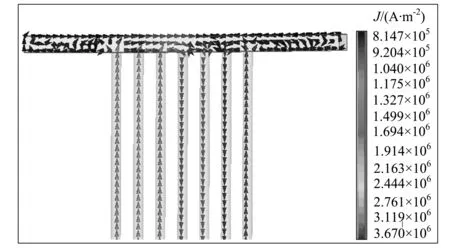
图7 阻尼绕组电流密度矢量图(20 ms时刻)Fig.7 Current Density Vector in the Damping Winding

电流密度的精确计算对于判断电机的热负荷情况、铜耗计算至关重要,会影响到电机的温升和耗材,是绕组设计的重要依据。另外它还是准确计算电磁力、电机应力场和机械强度的必要前提。

2.2 磁通量密度分布

如图8所示，主磁通的路径是由转子主磁极出发,经过极靴、气隙、定子槽齿、定子铁心之后,再穿过气隙,到达相邻磁极,通过转子铁心构成一个闭合磁路。

图8 磁通量密度矢量图(20 ms时刻)Fig.8 Magnetic Flux Density Vector In Model

如图9所示,磁极处磁密最大,槽齿处磁密也较大,轭部和相邻两磁极交界处的磁密较小。这是因为转子磁极被励磁绕组缠绕、定子槽内装有绕组,当励磁绕组和定子绕组通入电流后,在其周围产生了磁场,铁心材料的导磁率很大,磁力线大多从铁磁材料中通过,因而磁极和槽齿处的磁密较大。轭部由于距离源区较远,磁密相对较小。

图9 磁通量密度云图(20 ms时刻)Fig.9 Magnetic Flux Density Vector Cloud

从三维云图中还可以看到磁场在电机轴向方向上不是均匀分布的,在中平面处磁密更大。当铁心材料、频率、硅钢片厚度一定时,铁耗只决定于磁通密度的最大值,准确计算电机的磁密分布是正确计算电机铁耗的前提,同时也是计算电机应力分布的重要依据[12]。

2.3 气隙磁密计算

空气隙是定子和转子间电能-机械能转换的枢纽,其中磁场的分布和变化规律与电机中的功率转换、传递有着密切联系。气隙磁密的大小、波形与电机的运行状况、损耗、性能密切相关,是电机的重要参数。

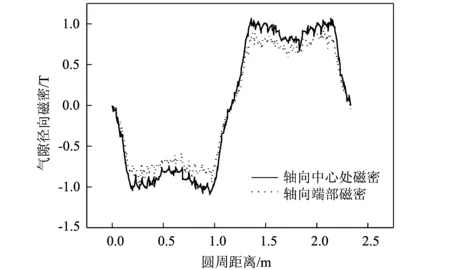
图10 轴向中心及端部气隙磁密(20 ms时刻)Fig.10 Air Gap Flux Density in Axial Center and that in End

该发电电动机为凸极机,定子侧存在齿槽,因此气隙不是均匀的,电机运行时会有谐波存在,使气隙磁密波形产生畸变。转子磁极上装有阻尼绕组,在交变磁场中会产生感应涡流,感应涡流也会对气隙磁场产生影响,体现在磁密的波峰处出现下凹情况。考虑到电机的端部效应对气隙磁密分布的影响[13],取电机轴向中心处截面和端部截面的二维气隙磁密如图10所示,气隙磁密沿轴向的大小不是恒定值,由于端部漏磁通的影响,靠近端部的气隙径向磁密要小于轴向中心处的。

对电机轴向中心截面处的气隙磁密做傅里叶分解如图11所示,气隙磁密基波和各次谐波的变化规律,其中除基波外,三次谐波的幅值最大,其余谐波很小。

图12是对图11中合成磁密进行傅里叶谐波分解至21次谐波后得到的各次谐波频谱图。其基波幅值约为1.11 T,其余谐波中三次谐波幅值最大,约为0.36 T,其余谐波幅值相对较小。

谐波会使发电电动机损耗增大,产生附加发热,导致电机温升过高,使得电机效率下降。还会引起绕组的温度分布不均匀,导致绝缘层破坏、电机转矩脉冲及噪声的增加[14]。因此在电机的优化设计中采取适当手段对谐波进行抑制是非常有必要的。

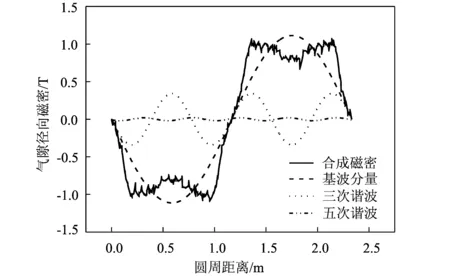
图11 轴向中心处气隙磁密及其傅里叶分解Fig.11 Air Gap Magnetic Flux Density in Axial Center and Fourier Decomposition on It

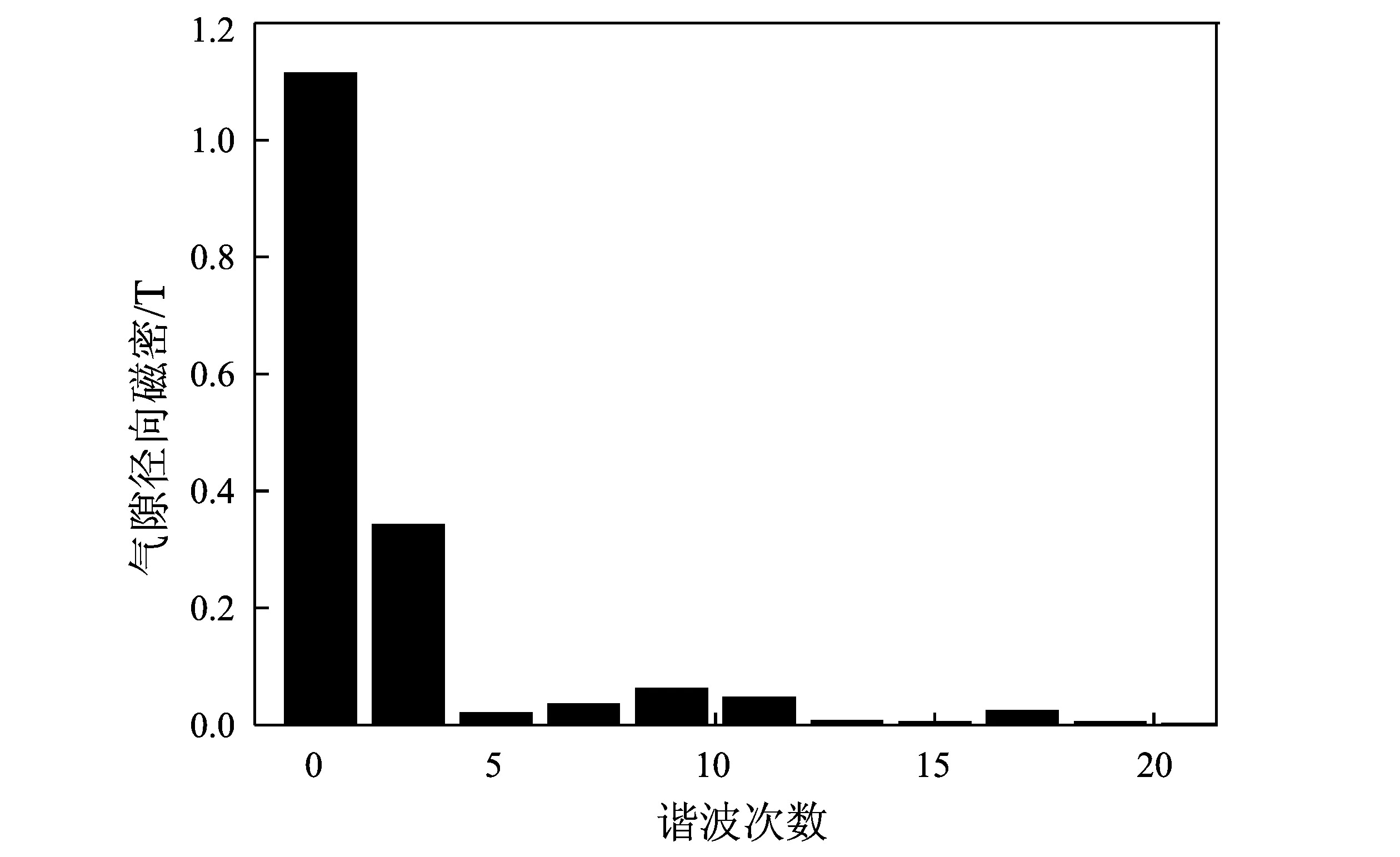
图12 气隙磁密分解频谱图Fig.12 Frequency Spectrogram of Air-Gap Flux Density

3 结束语

针对广州抽水蓄能B厂某大型发电电动机建立了三维模型,利用有限元法,对该电机进行了三维瞬态涡流场计算,对电流密度、磁场分布和气隙磁密等进行了分析说明,得到了良好的计算结果。三维模型考虑了端部效应,更能模拟实际电机,能够得到与实际电机相近的电流密度和磁场分布,计算结果较为准确,可以为发电电动机的设计、选型、国产化制造提供一定的参考依据。

[1] 张滇生.抽水蓄能在南方电网中的作用研究[J].水力发电,2010,36(9):1-3,11.

[2] 梅祖彦.抽水蓄能发电技术[M].北京:机械工业出版社,2000.

[3] 王 楠,白建华,刘贵元,等.国外抽水蓄能电站发展经验及相关启示[J].中国电力,2009,42(1):89-92.

[4] 赵 政.发电电动机的安全稳定运行[J].大电机技术,2011,(3):13-16.

[5] 陆佑楣,潘家铮.抽水蓄能电站[M].北京:水利水电出版社,1992.

[6] 赵 政.发电电动机的比较设计[J].西北水电,2012,增刊1:116-121.

[7] 鲁长彬,苗立杰.水轮发电机水内冷定子温度场的分析方法[J].大电机技术,2000,(3):1-4.

[8] Khan G KM,Buckley G W.An Integrated Approach for the Calculation of Loss and Temperatures in the End-region of Large Turbine Generators[J].IEEE Transactions on Energy Conversion,1990,5(1):183-194.

[9] 谢德馨,姚缨英,白保东,等.三维涡流场的有限元分析[M].北京:机械工业出版社,2001.

[10] 黄国治,傅丰礼.中小旋转电机设计手册[M].北京:中国电力出版社,2007.

[11] 李觉民,郭立炜.常用铁磁材料的有效磁导率和磁阻率及其解析表达式[J].哈尔滨电工学院学报,1998,11(4):324-330.

[12] 闫 锋,玉佳彬.超高效电机的关键制造技术[J].电机控制与应用,2013,40(7):9-13.

[13] 宋文宇,张宇娇,吴艳秋,等.十五相电机电磁场的三维有限元分析[J].电机控制与应用,2013,40(6):7-10.

[14] 吴艳红,王鸿鹄,周玮杰.时间谐波对电机空载铁心损耗的影响[J].电机控制与应用,2013,40(2):14-18.

(编辑：刘笑达)

Transient Eddy Current Field Analysis of Pumped-Storage Generator-Motor Using Three Dimensional Finite Element Method

ZHANG Yujiao1,QIN Weinan1,2,DONG Xiaohu3,ZHENG Yong4

(1.CollegeofElectricalEngineeringandNewEnergy,ChinaThreeGorgesUniversity,Yichang443002,China;2.StateGridJinhuaPowerSupplyCompany,Jinhua321001,China;3.CSGPowerGenerationCompanyMaintenanceandTestCenter,Guangzhou511400,China;4.HubeiBaulianhePumpedStorageCo.,LTD.,StateGridXinyuanCompany,Huanggang438600,China)

Pumped-storage power plant is extensively used in power system because of its excellent performance in peak load and frequency regulation and emergency reserve. Generator-motor is an important part of pumped-storage power plant and plays a key role in the operation of the whole power plant.Consequently,the safe and stable running of the power plant and even the power grid is directly influenced by the performance of generator-motor. This paper offers a 3-D transient eddy current field calculation on generator-motor of Guangzhou B pumped-storage power plant using finite element method. A 3-D generator-motor model is presented in this paper.The distribution of current density and flux density is educed,the radial air-gap flux density is obtained and the harmonic analysis is carried out.Through the calculation on 3-D transient eddy field of generator-motor, the distribution of motor electromagnetic field might be more accurately represented.The calculation result can offer reference for the design, model selection and localized manufacturing of motor.

pumped storage;generator-motor;finite element analysis;transient eddy current field analysis;3D calculation

1007-9432(2015)04-0424-06

2014-09-04

国家自然科学基金项目:面向电磁装置虚拟设计的物理场耦合异型网络映射研究(51207081)；三峡大学硕士学位论文培优基金项目(2014PY027)

张宇娇(1979-)，女，湖北武汉人,博士，副教授，主要从事电力设备及电磁装置多物理场耦合数值分析及机辅设计，(Tel)15871559339,(E-mail)jiao_zyj@163.com

TM 15

A

10.16355/j.cnki.issn1007-9432tyut.2015.04.012